Řešení elektrických obvodů

Teoretické základy k této kapitole jsou obsaženy ve skriptech Elektronika, kapitola 1.

1. část:

 výkon, práce
 efektivní hodnoty proudu a napětí
  pasivní součásti elektrických obvodů
 komplexní impedance

Následující: 

2. část:

 analýza elektrických obvodů:

3. část:

 rezonance
 Fourierovy řady
 třífázové sítě
 elektromagnetická indukce

Příklad 1.1:

Dva zdroje konstantního napětí U₁=20 V a U₂=50 V jsou zařazeny do obvodu na obr. 1.1.1. Jaký výkon dodává do obvodu každý z nich?

Řešení

Nápověda

Teorie: Kirchhoffovy zákony

Příklad 1.2:

V obvodu na obr. 1.2.1 je u(t) = 150 sin(ωt) V a R=25 Ω. Spočtěte proud i(t), okamžitý výkon p(t) a průměrný výkon P.

Řešení 

Nápověda

Příklad 1.3:

V obvodu na obr. 1.3.1 je proud i₂(t)=6sinωt A a R₁=10 Ω, R₂=5 Ω, R₃=15 Ω.
a) Vypočtěte proudy i₁(t) a i₃(t) a napětí u_AB  a u _BC.
b)Spočtěte okamžité a průměrné hodnoty výkonů spotřebovaných na rezistorech   R₁, R₂, R₃.

Řešení

Nápověda

Příklad 1.4:

Indukční motor má výkon P=2 hp a jeho účinnost η=85%. Účiník je cos α=0,8. Vypočtěte zdánlivý výkon S a jalový výkon Q.

Řešení

Nápověda

Příklad 1.5:

Vypočtěte práci střídavého proudu i(t)= I₀sin(ωt) ve vodiči s ohmickým odporem R za jednu periodu T.

Řešení

Nápověda

Příklad 1.6:

Jaký proud spotřebuje elektromotor na střídavý proud, jestliže při napětí U_ef=230 V má výkon P=2208 W, účiník cosφ=0,88 a účinnost elektromotoru je η=0,89?

Řešení

Nápověda

Příklad 1.7:

Spotřebič s příkonem P_p=3 kW a účiníkem cosφ₁=0,6 je připojen na elektrickou síť s efektivní hodnotou napětí U_ef=230 V a frekvencí f=50 Hz.
a) Jak velký kondenzátor je třeba připojit paralelně ke svorkám spotřebiče, abychom účiník zvýšili na cosφ₂=0,9?
b) Jaký by musel být kondenzátor, aby nenastalo fázové posunutí mezi napětím a proudem (cosφ₂=1)?

Řešení

Nápověda

Příklad 1.8:

Vypočtěte výkon střídavého proudu ve spotřebiči, jestliže ampérmetr ukazuje proud I=2 A a voltmetr připojený na svorky spotřebiče ukazuje napětí 110 V. Předpokládejte, že účiník je cosφ=0,8.

Řešení

Nápověda

Příklad 1.9:

Spočtěte průměrnou a efektivní hodnotu funkce y(t) = Y_msinωt.

Řešení

Nápověda

Teorie

Příklad 1.10:

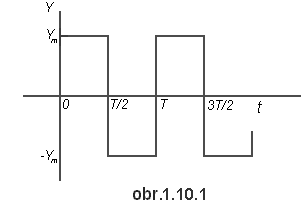
Spočtěte průměrnou a efektivní hodnotu funkce obdélníkového průběhu (obr. 1.10.1).

Řešení

Nápověda

Teorie

Příklad 1.11:

Spočtěte průměrnou a efektivní hodnotu funkce pilového průběhu (obr. 1.11.1).

Řešení

Nápověda

Teorie

Příklad 1.12:

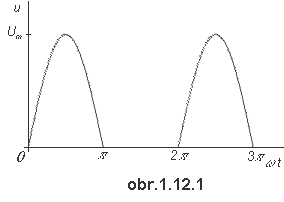
Spočtěte průměrnou a efektivní hodnotu jednocestně usměrněného sinového průběhu napětí (obr. 1.12.1).

Řešení

Nápověda

Teorie

Příklad 1.13:

Spočtěte střední hodnotu u_stř. a efektivní hodnotu U_ef dvoucestně usměrněného střídavého napětí podle obr. 1.13.1. Dále spočtěte průměrný výkon na rezistoru o odporu R, na který je toto napětí přiloženo.

Řešení

Nápověda

Teorie

Příklad 1.14:

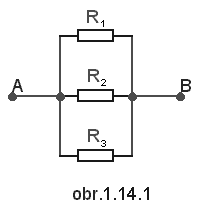
Odvoďte vztah pro celkový odpor R paralelního zapojení tří rezistorů podle obr. 1.14.1.

Řešení

Nápověda

Příklad 1.15:

Odvoďte vztahy pro dělící poměr děliče napětí (obr. 1.15.1) a děliče proudu (obr. 1.15.2).

Řešení

Nápověda

Teorie: Kirchhoffovy zákony

Příklad 1.16:

Na cívce s indukčností L=0,2 H je napětí u(t)=150sin(1000t) V.Spočtěte proud i(t) procházející cívkou, okamžitý výkon p(t) a průměrný výkon P na cívce.

Řešení

Nápověda

Příklad 1.17:

Stanovte časový průběh proudu ideální cívkou o indukčnosti L, která je připojena na zdroj konstantního napětí U.

 Řešení

Nápověda

Příklad 1.18:

Odvoďte vztahy pro celkovou indukčnost sériového a paralelního spojení dvou cívek.

Řešení

Nápověda

Příklad 1.19:

Proud i(t), jehož průběh je znázorněn na obr. 1.19.1, je proud v ideální cívce o indukčnosti L. Spočtěte hodnotu L, jestliže napětí dosahuje špičkové hodnoty U_m=100 V. Načrtněte průběh napětí.

Řešení

Nápověda

Příklad 1.20:

Odvoďte vztahy pro celkovou kapacitu sériového a paralelního spojení dvou kondenzátorů.

Řešení

Nápověda

Příklad 1.21:

Na kondenzátor o kapacitě C je připojeno napětí u(t)=U_msin(ωt). Spočtěte proud i(t), výkon p(t), náboj na kondenzátoru q(t) a energii w(t) elektrického pole v kondenzátoru. Uvažujte w(t=0)=0.

Řešení

Nápověda

Příklad 1.22:

Na kondenzátor o kapacitě C=60 μF je přiloženo napětí u(t), jehož časový průběh je na obr. 1.22.1. Načrtněte průběh okamžitého proudu i(t), okamžitého výkonu p(t) a určete maximální hodnoty proudu I_m a výkonu P_m.  

Řešení

Nápověda

Příklad 1.23:

V sériovém RL obvodu je R=5 Ω a L=2 mH. Na obvod je přiloženo napětí u(t)=150sin(5000t) V. Spočtěte celkovou impedanci Z.

Řešení

Teorie

Příklad 1.24:

V sériovém RC obvodu je R=20Ω, C=5 μF. Na obvod je přiloženo napětí u(t)=150cos(10000t) V. Spočtěte celkovou impedanci Z.

Řešení

Teorie

Příklad 1.25:

V sériovém LC obvodu je L=4 mH a C=50 μF. Na obvod je přiloženo napětí u(t)=230sin(500t) V. Spočtěte celkovou impedanci Z.

Řešení

Teorie

Příklad 1.26:

Odpor R₁ a indukčnost L cívky byly měřeny následujícím způsobem. Cívka byla zapojena do série s rezistorem o odporu R=10 Ω a měřilo se napětí na cívce U_C, napětí na rezistoru U_R a napětí na celém obvodu U. Při frekvenci proudu f=50 Hz byly naměřeny hodnoty U_R=20 V, U_C=22,4 V, U=36 V. Určete R₁ a L.

Řešení

Nápověda

Příklad 1.27:

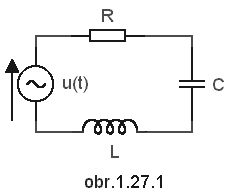
Jaký proud prochází obvodem na obr. 1.27.1, je-li R=10 Ω, C=2 μF, L=0,1 H, u(t)=325e^jωt V?

Řešení

Nápověda

Příklad 1.28:

Sériovým spojením tlumivky a kondenzátoru s kapacitou C=10 μF prochází proud s efektivní hodnotou I_ef=1 A. Obvod je připojen na napětí efektivní hodnoty U_ef=120 V frekvence f=50 Hz (obr. 1.28.1). Ohmický odpor tlumivky je 120 Ω. Vypočtěte velikost vlastní indukčnosti tlumivky.

Řešení

Nápověda

Příklad  1.29:

Mějme obvod na obr 1.29.1, kde C=16 μF, R=200 Ω, u(t)=325e^j100π V. Určete impedanci Z obvodu, proud i(t) v obvodu, fázové posunutí mezi napětím a proudem a průběh napětí na kondenzátoru a rezistoru.

Řešení

Nápověda

Následující: 

2. část:

 analýza elektrických obvodů:

3. část:

 rezonance
  Fourierovy řady
  třífázové sítě
  elektromagnetická indukce