Komplexní impedance

Mějme sériový RL obvod s generátorem střídavého napětí u(t)=U_me^jω t (obr. 1). Podle 2. Kirchhoffova zákona je .
Toto je lineární diferenciální rovnice prvního řádu, která má partikulární řešení ve tvaru i(t)=Ke^jω t Po dosazení do rovnice dostaneme
,
z čehož je a tedy .
Impedance Z=u(t)/i(t)=R+jω L je komplexní číslo s reálnou částí R a imaginární částí ω L.

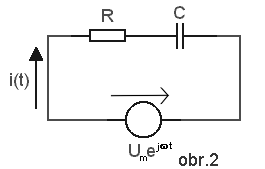
Nyní vezměme sériový RC obvod se stejným generátorem napětí (obr. 2). Podle 2. Kirchhoffova zákona je . Opět položíme i(t)=Ke^jω ta máme , z čehož .
Tedy .
Impedance Z=u(t)/i(t)=R-j/ω C je opět komplexní číslo s reálnou částí R a imaginární částí -1/ωC.

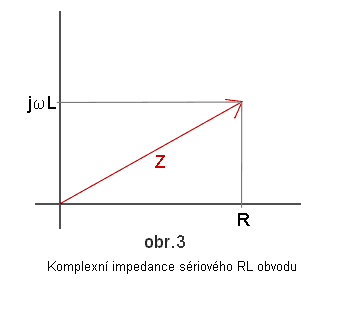
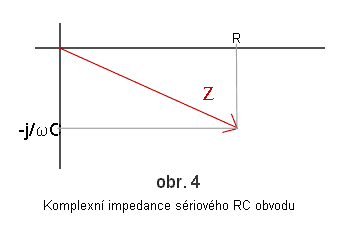
Prvky elektrických obvodů můžeme popisovat jejich komplexní impedancí. Rezistor má komplexní impedanci R, cívka jωL a kondenzátor -j/ωC.

Jelikož je komplexní impedance komplexním číslem, můžeme ji znázornit v komplexní rovině. Dostaneme fázorový diagram (obr. 3, 4).
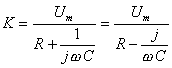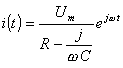