 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
V této kapitole dovršíme fenomenologický popis elektrických a magnetických polí v jeho vrcholné syntetické podobě vyjádřené soustavou Maxwellových rovnic. Na tato pole nebudeme již klást omezující podmínky, budeme je považovat za obecně libovolně proměnná v čase i prostoru, tj. za nestacionární. Předpoklad o nestacionárním charakteru elektrického a magnetického pole má za následek jejich vzájemnou závislost, vazbu, vyjádřenou odpovídajícími členy v Max-wellových rovnicích.
Uvedená skutečnost vede k přirozenému předpokladu o existenci obecnějšího elektromagnetického pole; vzájemně závislé nestacionární elektrické a magnetické pole tvoří jeho součásti. Elektrostatické pole, stacionární elektrické a magnetické pole a kvazistacionární elektrické a magnetické pole probíraná v předchozích kapitolách jsou jen zvláštními případy tohoto obecného pole. Jak uvidíme, je představa o elektromagnetickém poli nejen teoretickou syntézou těchto zvláštních případů, ale i důsledkem dalších nezávislých experimentálních poznatků, především poznatků o elektromagnetických vlnách. Obecné elektromagnetické pole je dokonce pojem v jistém smyslu primární, neboť má smysl i v mikroskopickém měřítku, zatímco dříve vyšetřované typy statických, stacionárních a kvazistacionárních polí mají smysl jen v makroskopickém pohledu a jsou středními hodnotami tohoto mikroskopického elektromagnetického pole.
Maxwellova teorie dovršuje nejen syntézu
elektrických a magnetických jevů, ale i jevů optických. Světlo představuje jen
část širokého spektra elektromagnetických vln. Formálně matematickým výrazem
této skutečnosti je to, že v Maxwellových rovnicích vystupuje vedle
relativní permitivity a permeability, popisujících elektrické a magnetické
vlastnosti prostředí, konstanta c
daná vztahem
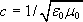a představující rychlost světla ve vakuu.
Zatímco permitivita vakua ε
0 a permeabilita vakua μ
0
jsou konstanty zavedené uměle v soustavě jednotek SI, má jejich součin
fyzikální smysl převrácené hodnoty čtverce rychlosti světla ve vakuu a jeho
přítomnost v Maxwellových rovnicích je zdůvodněna fyzikálně.
Poznamenejme (viz též čl. 1.1.1), že takové postupné "sjednocování interakcí", kdy se ukazuje, že elektrické, magnetické a optické jevy jsou vlastně projevy obecnější interakce elektromagnetické, odpovídá vývoji současného fyzikálního poznání. V osmdesátých letech dvacátého století bylo teoreticky i experimentálně prokázáno, že elektromagnetické působení je opět zvláštním případem ještě obecnější tak zvané elektroslabé interakce. Tato interakce zahrnuje vedle elektromagnetických též tak zvané slabé síly projevující se při beta radioaktivním rozpadu atomových jader a též v některých jaderných reakcích za účasti neutrina. Pro tyto slabé síly je charakteristické, že se mění při zrcadlovém zobrazení a vnášejí tak do přírody prostorovou asymetrii. Je pravděpodobné, že i elektroslabé interakce se ukáží být zvláštním případem obecnějších interakcí zahrnujících i silné jaderné síly a gravitaci.
Také v této kapitole, podobně jako v kapitolách l, 3 a 4, budeme zpočátku pojednávat o makroskopickém elektromagnetickém poli, které můžeme přímo pozorovat a měřit našimi přístroji. Je to právě pole, které vystupuje v Maxwellových rovnicích. Naproti tomu v kapitole 2 jsme uvažovali pole pohybujících se bodových elektrických nábojů ve vakuu a vycházeli jsme přitom ze speciální teorie relativity. Pole takto idealizovaných soustav pohybujících se nábojů nás přivádí k mikroskopickému modelu látkového prostředí, které můžeme považovat prostě za soustavu nábojů rozložených určitým (velmi komplikovaným) způsobem ve vakuu a pohybujících se určitým (velmi komplikovaným) způsobem v prostoru a čase. Tyto náboje pak vytvářejí v každém bodě prostoru a v každém okamžiku mikroskopické elektromagnetické pole, charakterizované rychlými změnami a často obrovskými intenzitami. Toto pole popisované takzvanými Lorentzovými rovnicemi bude předmětem našeho zájmu v poslední oddílu 5.4 a tam také ukážeme souvislost mezi polem mikroskopickým a makroskopickým.
|
|
|
|
|
|