Podle veškeré dosavadní zkušenosti jsou fyzikální jevy v souladu se zákony zachování energie a hybnosti. Pro danou soustavu je však vždy nutné určit konkrétní možné formy energie a jejich přeměn. Uvažujme nyní fyzikální soustavu nabitých částic v elektromagnetickém poli. Předpokládejme například, že v prostoru je určitým způsobem rozložen volný elektrický náboj s objemovou hustotou ρ ( r , t), jehož pohyb je popsán polem rychlostí v ( r , t). Určeme energii, kte-rou uvažované elektromagnetické pole dodá tomuto náboji.
Podle Lorentzova vzorce (3.56) můžeme vyjádřit hustotu síly f , kterou elektromagnetické pole působí na takto rozložený prostorový náboj
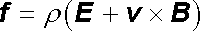 . . |
(5.40) |
Pro výkon n dodávaný elektromagnetickým polem do jednotkového objemu plyne
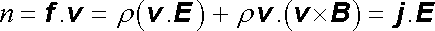 . . |
(5.41) |
Vyjádříme-li proudovou hustotu j z Maxwellovy rovnice pro rot H (5.21) , můžeme výraz (5.41) upravit na tvar
 . . |
(5.42) |
Z Maxwellovy rovnice pro rot E (5.21) můžeme skalárním vynásobením H vytvořit obdobu výrazu na pravé straně (5.42)
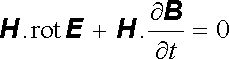 |
(5.43) |
a sečtením (5.42) a (5.43) výraz pro hustotu výkonu n symetrizovat na tvar
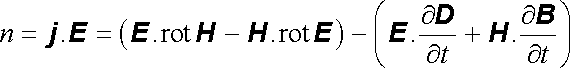 . . |
(5.44) |
Podle (D 1.55) platí
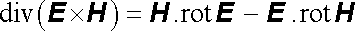 , , |
(5.45) |
takže dostáváme výsledek
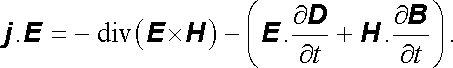 |
(5.46) |
Rovnice (5.46) nemá zatím jasný fyzikální smysl. Víme o ní pouze tolik, že člen na její levé straně vyjadřuje výkon dodaný polem do jednotkového objemu, takže zbylé členy musí mít také fyzikální rozměr hustoty výkonu. Dále víme, že rovnice je přímým důsledkem obecných Maxwellových rovnic, takže jako celek musí platit pro libovolné elektromagnetické pole.
Abychom mohli podat její fyzikální interpretaci, budeme uvažovat poněkud konkrétnější situaci. Především předpokládejme, že v uvažovaném prostředí platí materiálové vztahy D = ε E , B = μ H , přičemž konstanty ε , μ nezávisí na čase. Jde tedy o lineární měkké prostředí. Poslední člen na pravé straně (5.46) pak můžeme upravit na
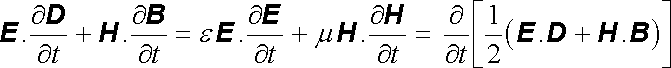 . . |
(5.47) |
Zavedeme označení
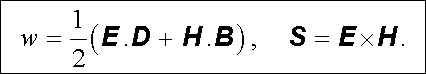 |
(5.48) |
Vztah (5.46) lze pak zapsat kompaktním způsobem jako
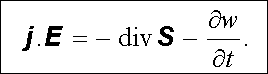 |
(5.49) |
Všimněme si, že veličina w má fyzikální rozměr objemové hustoty energie a je součtem výrazů (1.267) a (4.100) , které jsme interpretovali jako hustotu energie elektrického a magnetického pole. Veličina S představuje vektor kolmý k vek-torům intenzity elektrického a magnetického pole a má rozměr hustoty toku energie J. m-2.s-1. Navíc v části prostoru bez volných nábojů, kde j = 0 , má rovnice (5.49) tvar
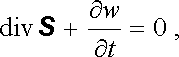 |
(5.50) |
který je formálně shodný s rovnicí kontinuity proudu (3.15) . Tato rovnice, jak víme, vyjadřuje zákon zachování elektrického náboje, a je proto nasnadě interpretovat rovnici (5.50) jako diferenciální (lokální) tvar zákona zachování energie v té části prostoru, v níž nepůsobí zdroje energie ani nenastávají její ztráty.
Konkretizujme dále, že proudová hustota j představuje hustotu kondukčního proudu ve vodiči splňujícím Ohmův zákon v obecném tvaru (3.26) . Potom můžeme psát
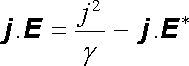 , , |
(5.51) |
kde E * představuje vtištěnou (elektromotorickou) intenzitu. Rovnici (5.49) pak přepíšeme na
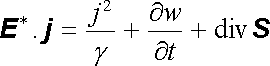 . . |
(5.52) |
Zvolme nyní libovolnou uzavřenou plochu Σ , jíž nemohou pronikat částice a která ohraničuje objem V, a vypočtěme objemový integrál z pravé i levé strany poslední rovnice:
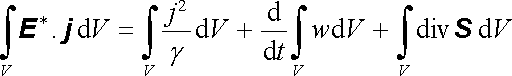 . . |
(5.53) |
Poslední člen na pravé straně můžeme převést na plošný integrál užitím Gaussovy věty (D 1.32). Dostaneme výsledek
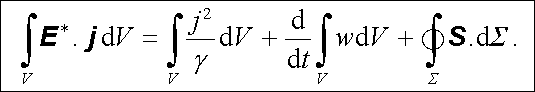 |
(5.54) |
Tato rovnice zřejmě představuje energetickou bilanci v objemu V. Člen na levé straně vyjadřuje výkon dodávaný do objemu V vtištěnými intenzitami E *. Část této energie se v tomto objemu nevratně mění na Jouleovo teplo; vyjadřuje to první člen na pravé straně. Integrál v druhém členu představuje součet integrálů (1.266) a (4.99) , a lze jej tedy chápat jako energii elektromagnetického pole připadající na objem V. Celý druhý člen pak bude mít význam časové změny energie. Poslední člen na pravé straně představuje tok vektoru S plochou Σ . Nabízí se proto možnost interpretovat jej jako energii vytékající z objemu V.
Je-li možné právě uvedenou interpretaci jednotlivých členů rovnice (5.54) považovat za správnou, vyjadřuje tato rovnice zákon zachování energie v objemu V. Rovnice pak říká: Výkon dodaný do objemu vtištěnými intenzitami se spotřebuje jednak na Jouleovo teplo a na změnu energie elektromagnetického pole, jednak část tohoto výkonu vyteče plochou Σ ohraničující objem V.
Rovnice (5.54) byla odvozena J. H. Poyntingem, který také podal její interpretaci, uvedenou v předchozím výkladu. Nazývá se proto často Poyntingovou větou. Veličina S = E ℜ × H vyjadřující hustotu toku energie se nazývá Poyntingův vektor. Přesto, že rovnice (5.54) jako celek je důsledkem Maxwellových rovnic a její platnost je za uvedených podmínek nesporná, musíme uvedenou interpretaci jednotlivých jejích členů považovat za předpoklad, který vyžaduje experimentální ověření. Dosavadní experimentální zkušenost není však s touto interpretací v rozporu.
Připomeňme, že při odvozování výrazů (1.267) a (4.99) pro hustotu energie stacionárního či kvazistacionárního elektrického, respektive magnetického pole jsme zdůrazňovali, že jsme fyzikálně oprávněni hovořit pouze o celkové energii těchto polí v daném objemu, která odpovídá práci vynaložené na jejich vytvoření. Pojem objemové hustoty energie statických, resp. stacionárních polí byl přes svou plauzibilitu pouhým předpokladem, interpretací bez možnosti dát mu přímý experimentálně zdůvodněný smysl. Jiná situace je ovšem u obecného elektromagnetického pole. Poyntingův vektor zde představuje skutečnou, měři-telnou hustotu toku energie, jíž odpovídají změny skutečné objemové hustoty energie dané prvním z výrazů (5.48) .
Tato hustota energie elektromagnetického pole v měkkém lineárním prostředí zahrnuje ovšem jak energii samotného pole, tak i energii vynaloženou na polarizaci a magnetizaci prostředí. V případě vakua má elektromagnetické pole hustotu energie
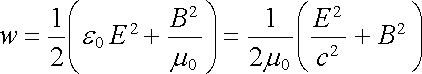 |
(5.55) |
a hustota jejího toku je rovna
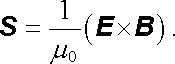 |
(5.56) |
Viděli jsme, že elektromagnetické pole působí na nabité částice silou o objemové hustotě (5.40) , která mění jejich energii. Z mechaniky však víme, že podle zákona síly se bude měnit také hybnost těchto částic. Můžeme proto usoudit, že i pro hybnost bude platit obdoba Poyntingovy věty (5.54) , vyjadřující zákon zachování: Hybnost dodávaná ohraničenému objemu V bude předávána jednak částicím, jednak elektromagnetickému poli v tomto objemu a může též ubývat vlivem toku hybnosti plochou Σ ven z tohoto objemu. Nositelem tohoto toku hybnosti mohou být přitom jak částice, tak elektromagnetické pole.
Hustota toku nějaké skalární veličiny představuje vektor. Jde-li přitom o veličinu vytékající z daného uzavřeného objemu, v němž nemůže ani vznikat, ani zanikat, bude úbytek této veličiny roven toku plochou Σ ohraničující tento objem. Omezíme se dále na případ objemu, jehož hranicí nepronikají částice. Pro energii W elektromagnetického pole v objemu V bude v tomto případě její bilance vyjádřena vztahem
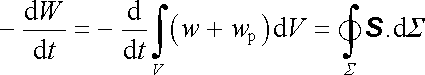 , , |
(5.57) |
kde S je Poyntingův vektor, w hustota energie pole a wp hustota energie částic. Podle (5.41) platí
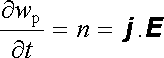 , , |
(5.58) |
takže v diferenciálním tvaru přechází (5.57) na (5.49) .
Podobně budeme postupovat v případě hybnosti. Označme předpokládanou objemovou hustotu hybnosti elektromagnetického pole g , hybnost částic v jednotkovém objemu p , celkovou hybnost v objemu V symbolem Π a tok hybnosti elektromagnetického pole plochou Σ jako Ξ . Potom můžeme vyjádřit bilanci hybnosti vztahem
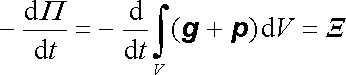 . . |
(5.59) |
Víme, že tok skalární veličiny danou plochou je dán integrálem skalárního součinu dvou vektorů charakterizujících jediné dva význačné směry - směr proudění dané veličiny (vyjadřuje jej vektor hustoty toku) a směr normály k dané ploše. Hustota toku skalární veličiny je tedy vektor. Složitější je ovšem situace, uvažujeme-li tok nějaké vektorové veličiny, například hybnosti. V tomto případě přibývá další směr daný vektorem hybnosti. Hustota toku vektorové veličiny má pak charakter tenzoru, tedy veličiny určené dvěma indexy i, k, kde hodnoty 1, 2, 3 těchto indexů odpovídají složkám ve směru os x, y, z. Při přechodu k jiné soustavě souřadnic se složky tenzorů transformují jako součiny odpovídajících složek vektorů.
V uvažovaném případě můžeme i-tou složku toku hybnosti elektromagnetického pole plochou Σ vyjádřit integrálem
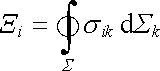 , , |
(5.60) |
kde σ ik představuje takzvaný tenzor napětí a v integrálu se rozumí sčítání přes index k od l do 3. Složky tenzoru napětí mají fyzikální rozměr objemové hustoty energie, který je týž jako rozměr tlaku či mechanického napětí, tj. N.m-2. Je to tenzor dobře známý z mechaniky kontinua, kde udává sílu působící na jednotku plochy - tlakovou, tahovou nebo smykovou.
Plošný integrál na pravé straně (5.60) lze pomocí věty tenzorového počtu analogické k větě Gaussově převést na integrál objemový
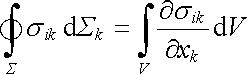 . . |
(5.61) |
Výraz
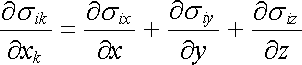 |
(5.62) |
můžeme považovat za i-tou složku vektoru, který má charakter divergence tenzorové veličiny σ ik.
Bilanci i-té složky hybnosti můžeme tedy podle (5.59) až (5.61) vyjádřit v integrálním tvaru jako
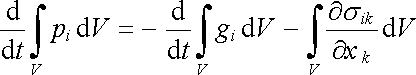 |
(5.63) |
a v diferenciálním tvaru
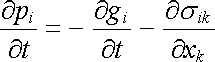 . . |
(5.64) |
Podle Newtonova zákona síly bude pro hustotu síly f danou (5.40) platit
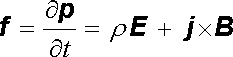 . . |
(5.65) |
Vyjádříme-li hustoty ρ a j z Maxwellových rovnic (5.21) , dostaneme
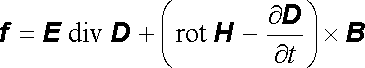 . . |
(5.66) |
K pravé straně (5.66) přičteme nulové vektory
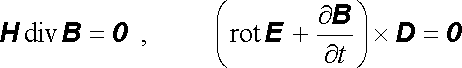 , , |
(5.67) |
které z Maxwellových rovnic vyplývají. Tak dostaneme symetrický výraz pro hustotu síly
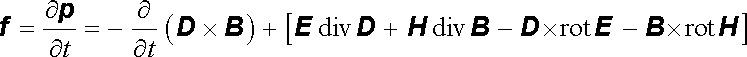 . . |
(5.68) |
Nyní porovnáme složkovou rovnici (5.64) a vektorovou rovnici (5.68) . Vidíme, že tyto rovnice si budou odpovídat, bude-li objemová hustota hybnosti elektromagnetického pole rovna
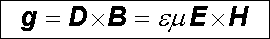 |
(5.69) |
a podaří-li se upravit výraz v hranaté závorce na pravé straně rov. (5.68) na tvar ℜ ∂ σ ik/ℜ ∂ xk. Tato poněkud komplikovanější úprava, kterou zde nebudeme provádět (viz např. [3]), vede na tenzor
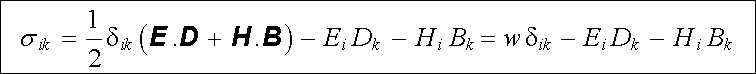 |
(5.70) |
nazývaný Maxwellovým tenzorem napětí (δ ik je Kroneckerův symbol rovný nule při i ℜ ≠ k a rovný jedné při i = k).
Objemová hustota hybnosti (5.69) zahrnuje ovšem jak hybnost elektromagnetického pole, tak i hybnost vázaných nábojů v látkovém prostředí. Ve vakuu máme
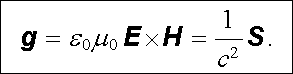 |
(5.71) |
Hustota hybnosti souvisí tedy jednoduchým vztahem (5.71) s hustotou toku energie. Tento vztah má ve speciální teorii relativity obecnou platnost.
Uvedené výsledky svědčí o tom, že elektromagnetickému poli lze přiřadit takové mechanické veličiny, jako je objemová hustota energie, hustota toku energie, objemová hustota hybnosti, tenzor napětí, a jak lze ukázat (viz např. [3]), i hustota momentu hybnosti. Všechny tyto vlastnosti elektromagnetického pole jsou přitom v dobré shodě s experimentální zkušeností, která je potvrzuje se stále větším stupněm jistoty. Není proto důvodu považovat elektromagnetické pole za méně hmotný objekt, než jsou látková tělesa.
Termodynamika se zabývá fenomenologickým popisem obecných vlastností a zákonitostí chování makroskopických fyzikálních soustav, především vlastnostmi jejich rovnovážných stavů a přechodů mezi těmito stavy. Makroskopické soustavy jsou tvořeny velkým množstvím částic zaujímajících určitý objem a vystavených působení vnitřních i vnějších sil. Termodynamika přitom pohlíží na tyto soustavy částic (plyn, kapalinu, těleso v pevném skupenství, dielektrikum, magnetikum apod.) jako na kontinuum a odhlíží od jejich vnitřní struktury.[36] Základní termodynamická metoda spočívá ve vyšetřování bilance výměny energie a ve vyšetřování možných forem její výměny v dané soustavě. Termodynamika přitom rozeznává dvě základní formy výměny energie. První z nich je tzv. koherentní výměna energie, kdy všechna energie může být přeměněna v mechanickou práci spojenou se změnami makroskopických souřadnic soustavy. Druhá, nekoherentní forma výměny energie se nazývá teplo a jejím charakteristickým rysem je, že (obecně řečeno) všechna v mechanickou práci přeměněna být nemůže.
Termodynamické metody mohou být použity k vyšetřování vlastností libovolné fyzikální soustavy. Mají tudíž i nezastupitelné místo pro studium soustav vykazujících elektromagnetické jevy. Úkolem tohoto článku není řešení konkrétních úloh v takových soustavách, ale jen formulace základních termodynamických vztahů za přítomnosti elektromagnetického pole. V tomto smyslu představuje doplnění úvah prezentovaných v článku 5.2.1. Dříve však, než při-stoupíme k vlastnímu plnění uvedeného úkolu, krátce zrekapitulujeme nejzákladnější obecné termodynamické pojmy a zákony.
Stav dané termodynamické soustavy je obecně určen jednak stavem jednotlivých jejích součástí, jednak vnějšími podmínkami. Pro popis tohoto stavu je pak možné zavést tzv. vnitřní a vnější makroskopické parametry. Je-li například soustava tvořena určitým množstvím plynu, může být za vnitřní parametr považován jeho tlak, který je funkcí stavu jednotlivých molekul. Za vnější parametr může být naopak považován objem určený rozměry nádoby, v níž je plyn uzavřen. Ve stavu termodynamické rovnováhy (nebo ve stavu k ní blízkém) může být zavedena teplota T soustavy a hodnoty vnitřních parametrů jsou určeny jen hodnotami vnějších parametrů a teplotou.
Termodynamika používá k charakterizování stavu vyšetřované soustavy tzv. stavové veličiny. Nejdůležitější z nich jsou vnitřní energie U a entropie S, pomocí nichž lze vyjádřit základní termodynamické zákony. Důležitá je přitom skutečnost, že ve stavu termodynamické rovnováhy (nebo ve stavu k ní blízkém) jsou stavové veličiny rovněž jednoznačnou funkcí jen vnějších parametrů a teploty.
Při změně vnějších parametrů &ksi; i, dochází obecně ke změně stavu soustavy. Okolní tělesa mohou přitom působit na soustavu silami a konat mechanickou práci. Při malé změně vnějších parametrů δ &ksi; 1, δ &ksi; 2,... může být tato práce W vyjádřena vztahem
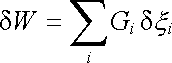 , , |
(5.72) |
v němž Gi představují zobecněné síly příslušející jednotlivým parametrům &ksi; i. Okolní tělesa však mohou soustavě dodávat současně i teplo. První zákon termodynamiky vyjadřuje energetickou bilanci mezi soustavou a okolními tělesy. Říká, že teplo δ Q a práce δ W dodané dané soustavě se rovnají změně její vnitřní energie δ U. Tedy
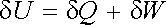 . . |
(5.73) |
Změna tepla dodaného soustavě souvisí se změnou entropie S. Podle druhého zákona termodynamiky nemůže entropie soustavy klesat; při nevratných procesech entropie vzrůstá, při vratných procesech zůstává konstantní. Výrazem druhého základního zákona termodynamiky je nerovnost
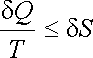 . . |
(5.74) |
Rovnost ve vztahu (5.74) přichází v úvahu pro vratné (kvazirovnovážné) procesy.
V daném rovnovážném stavu je stavovou veličinou rovněž tzv. volná energie definovaná vztahem
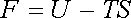 . . |
(5.75) |
Její význam spočívá v tom, že umožňuje přímo vyjádřit zobecněné síly Gi působící na soustavu a i její entropii. Platí
 . . |
(5.76) |
Zvláštní význam mezi termodynamickými procesy mají tzv. adiabatické procesy, při nichž stav soustavy není ovlivňován přenosem tepla z okolí. Adiabatické procesy nastávají tedy především v tepelně izolovaných soustavách, mohou však za ně být považovány i krátkodobé procesy v libovolných soustavách, při nichž lze přenos tepla s okolím zanedbat. Při vratném adiabatickém procesu se nemění entropie soustavy a δ S = δ Q/T = 0. Potom podle (5.73) máme
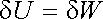 . . |
(5.77) |
Práce vnějších sil je tedy rovna změně vnitřní energie.
Obraťme nyní pozornost k řešení vlastního úkolu tohoto článku, tj. k formulaci termodynamických vztahů za přítomnosti elektromagnetického pole. Za tímto účelem budeme uvažovat makroskopickou soustavu vymezenou uzavřenou plochou Σ , která se nachází ve vnějším elektromagnetickém poli. Při formulaci termodynamických vztahů budeme vedle sil jiné fyzikální povahy, kterými na soustavu působí okolní tělesa, uvažovat ještě působení elektromagnetického pole přes hraniční plochu Σ , jehož charakter musí být ovšem v souladu s výsledky článku 5.2.1. Jelikož elektromagnetické pole představuje stejně reálnou fyzikální substanci jako látka, budeme pole uvnitř plochy považovat za součást naší soustavy.
Uvedené vymezení termodynamické soustavy přináší zcela novou fyzikální situaci. Experiment totiž ukazuje, že látky libovolného skupenství mohou vzhledem k svým vnitřním stupňům volnosti nejen absorbovat , ale i spon-tánně emitovat elektromagnetické záření, jehož intenzita i spektrální složení je silně závislé na teplotě. Obecně řečeno, i toto záření by mělo být považováno za součást uvažované soustavy a měly by být na ně aplikovány zákony termodynamiky. Uvedené záření má ovšem nekoherentní charakter a je - jak víme - odpovědné za přenos tepla mezi tělesy o různých teplotách. Ve stavu termodynamické rovnováhy mluvíme o rovnovážném záření. Z hlediska makro-skopické teorie může být považováno za fluktuace mikroskopických polí, a nebudeme je proto do dalších úvah zahrnovat.[37]
Interakce koherentního elektromagnetického pole s danou soustavou může být popsána na základě obecného vztahu (5.46) vyjadřujícího energetickou bilanci. Po integraci přes objem soustavy V a po převedení prvního členu pravé strany na plošný integrál přes plochu Σ ohraničující soustavu dostaneme
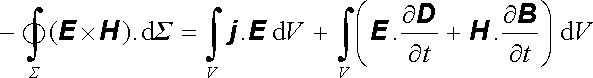 . . |
(5.78) |
Integrál na levé straně představuje výkon N dodávaný elektromagnetickým polem soustavě (tok nějaké veličiny vstupující danou plochou do uzavřeného objemu se bere jako záporný, tok vystupující jako kladný). Práce δ W vykonaná polem za krátký časový interval δ t bude pak rovna
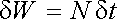 . . |
(5.79) |
Pro zjednodušení vyloučíme z úvah soustavy obsahující volné nositele proudu. Vezmeme-li v úvahu výsledky čl. 5.2.1 o objemovém rozložení energie v elek-tromagnetickém poli (srov. též články 1.5.5 a 4.3.2), můžeme vyjádřit obje-movou hustotu energie δ w dodávanou elektromagnetickým polem jako
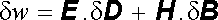 . . |
(5.80) |
Z tvaru (5.80) je vidět, že podle (5.72) lze intenzity E a H považovat za obecné síly, zatímco vektory indukce D a B hrají roli vnějších parametrů. Užitím uvedených výsledků je možné již jednoduše vyjádřit vnitřní i volnou energii soustavy. Vztáhneme-li všechny stavové veličiny na jednotkový objem a pří-slušné jejich hustoty označíme analogickými malými písmeny, dostaneme při vynechání neelektromagnetických interakcí
 . . |
(5.81) |
Podle (5.76) pak platí[38]
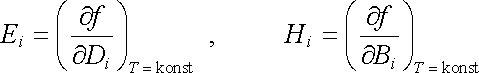 . . |
(5.82) |
V případě vratných adiabatických procesů lze s ohledem na (5.77) intenzity určovat přímo z vnitřní energie.
Vnitřní (resp. volná) energie soustavy, jak jsme ji zavedli, zahrnuje jak energii látkového prostředí ve vnějším poli, tak energii pole, které by existovalo bez přítomnosti tohoto látkového prostředí. Je účelné energii těchto polí E 0, B 0 od energie soustavy odečíst, a najít tak energii odpovídající pouze termodynamickému stavu tělesa. Pro dielektrikum jsme se zabývali touto otázkou v závěru článku 1.5.5, pro magnetikum v článku 4.3.2. Zjistili jsme, že hustoty přírůstku energie tělesa lze vyjádřit pomocí vektoru polarizace, resp. magnetizace jako
 . . |
(5.85) |
Změna celkové volné energie tělesa po odečtení změny energie vnějšího pole bude
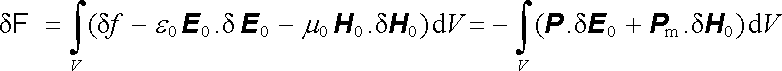 . . |
(5.86) |
Jsou-li vnější pole homogenní, dostaneme
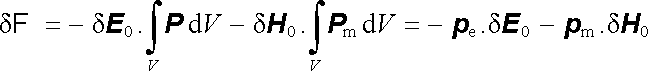 |
(5.87) |
(p e a p m jsou celkový elektrický a magnetický dipólový moment tělesa).
Pro diferenciál volné energie pak můžeme psát
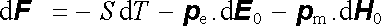 . . |
(5.88) |
Vidíme, že v soustavě tvořené látkovým tělesem ve vnějším elektrickém a magnetickém poli představují celkový elektrický a magnetický dipólový moment tělesa obecné síly a intenzity vnějších polí pak vnější parametry.