---

---

5.1 Maxwellovy rovnice

V kapitole 4 jsme na základě experimentálních výsledků formulovali obecný zákon elektromagnetické indukce. Podle tohoto zákona vzniká v uzavřeném obvodu elektrický proud vždy, když se jakýmkoliv způsobem mění magnetický indukční tok plochou ohraničenou obvodem. K vysvětlení uvedeného proudu jsme zavedli pojem indukovaného elektromotorického napětí E _F daného vzta­hem (4.2) . Ve všech případech uvažovaných v předchozí kapitole byl jev elek­tromagnetické indukce vázán vždy na určitý elektrický obvod, tedy pojímán integrálně.

Změna magnetického indukčního toku plochou obvodu může být vyvolána uměle vnějšími vlivy jako například mechanickým otáčením smyčky protékané proudem ve vnějším magnetickém poli nebo změnami magnetické indukce gene­rované vnějšími zdroji. Pomalu proměnný elektrický proud takto vznikající v obvodu vytváří proměnné elektrické pole, které můžeme pozorovat například mezi deskami kondenzátoru vloženého do obvodu a které jsme nazvali polem kvazistacionárním (viz článek 4.1.3). Experiment ukazuje, že takové pole je s dostatečnou přesností potenciální a vyhovuje vztahu (1.61) , popř. (1.63) a  (1.50) . Soustava rovnic pro časově proměnné elektrické a magnetické pole vytvářené kvazistacionárním, pomalu proměnným elektrickým proudem se pak neliší od stacionárního elektrického a magnetického pole diskutovaného v oddílech 3.2 a 3.3. Přitom však jev elektromagnetické indukce modifikuje okrajové podmínky řešení těchto rovnic (viz čl. 4.1.3). Zabýváme-li se pouze studiem obvodů s kvazistacionárními proudy (a například průmyslové kmitočty 50 nebo 60 hertzů u střídavých proudů předpoklad kvazistacionárnosti velmi dobře splňují), stačí zahrnout jev elektromagnetické indukce zavedením pojmu impedance do Ohmova a Jouleova zákona.

Přejdeme-li však k dostatečně vysokým kmitočtům, setkáme se s novými experimentálními jevy, jakým je například vyzařování elektromagnetických vln obvodem. Dodávaná energie se přitom mění jednak v Jouleovo teplo, jednak je unášena do prostoru. Tato skutečnost ukazuje, že kvazistacionární přiblížení nevyčerpává hloubku souvislosti mezi elektrickým a magnetickým polem a že je třeba přejít k ještě obecnějšímu popisu. Zbývá udělat poslední krok, o nějž se zasloužil právě Maxwell. Je přitom pozoruhodné, že toto poslední zobecnění provedl Maxwell na základě teoretických úvah dříve , než byly vlastnosti obecného elektromagnetického pole a elektromagnetických vln experimentálně pozorovány a prozkoumány.

Maxwellovo zobecnění zahrnuje dvě nové základní koncepce - představu o indukovaném elektrickém poli a o posuvném proudu.

5.1.1 pole

Představa o indukovaném elektrickém poli vznikla hlubokým domyšlením Fara­dayova zákona elektromagnetické indukce. Maxwell si položil otázku, je-li pro vznik jevu elektromagnetické indukce přítomnost uzavřené vodivé smyčky pod­statná, popřípadě je-li vůbec nutná přítomnost jakéhokoliv vodiče. Jde například o to, jak se bude chovat částice nesoucí náboj Q umístěná ve vakuu za přítom­nosti proměnného magnetického pole.

Má-li zákon elektromagnetické indukce platit zcela obecně, je nutné předpokládat, že časově proměnné magnetické pole je schopné vyvolat kon­vekční proud volných nabitých částic stejně dobře, jako je schopné vyvolat kon­dukční proud ve vodičích. Proto časově proměnné magnetické pole bude na uvedenou nabitou částici působit silou F , která je úměrná časové změně magnetického pole a není závislá na pohybu částice. Tuto sílu je možné popsat pomocí nového typu elektrického pole E _i které se nazývá indukovaným elektric­kým polem. Platí tedy

.

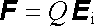(5.1)

Bude-li v daném bodě prostoru nenulové také stacionární elektrické pole E _s , vyvolané daným rozložením okolních nábojů, bude mít výsledná intenzita elektrického pole v místě částice hodnotu E = E _s + E _i. Celkovou sílu F působící na částici pohybující se rychlostí v bude možné opět vyjádřit Lorentzovým vzorcem (3.56)

.

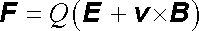Zde však má intenzita pole E nový, obecnější smysl. Představuje celkovou in­tenzitu elektrického pole daného jednak okamžitým rozložením nábojů v pro-storu, jednak hodnotou indukovaného elektrického pole, u něhož nemůžeme bezprostředně ukázat, které elektrické náboje jej vytvářejí. Toto celkové elektrické pole nazýváme nestacionárním elektrickým polem.

Existence indukovaného elektrického pole byla v Maxwellově době ovšem hypotézou. Maxwell předpokládal, že každá časová změna magnetického pole vyvolává vznik pole elektrického. Vznik indukovaného elektrického proudu je pak třeba považovat za projev tohoto elektrického pole v těch případech, kdy jsou v daném místě přítomni vhodní nositelé proudu. V dnešní době lze předpo­kládat uvedenou Maxwellovu hypotézu za plně experimentálně potvrzenou ve všech jejích důsledcích.

Nestacionární elektrické pole již ovšem není polem potenciálním. Abychom to ukázali, uvažujme libovolnou uzavřenou křivku l, nehybnou vůči pozorovací soustavě souřadnic. Při přenesení jednotkového náboje podél této křivky vykoná elektrické pole práci

.

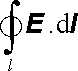(5.2)

Na druhé straně je třeba předpokládat, že podél křivky působí vždy indukované elektromotorické napětí E   _F, které je v případě nehybné křivky dáno vztahem (4.3) . Protože přenesení náboje podél křivky reprezentuje určitý proud I, můžeme zmíněnou práci vyjádřit také jako práci vykonanou tímto indukovaným elektromotorickým napětím. Za předpokladu, že přenesení náboje proběhne v krátkém časovém intervalu Δ t , je podle (3.41) tato práce rovna E _F IΔ t . Součin I Δ t představuje přenesený náboj, který jsme uvažovali jako jednotkový. Srovná­ním obou způsobů vyjádření pak dostaneme

.

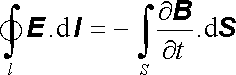(5.3)

Plošný integrál na pravé straně (5.3) může být počítán přes libovolnou plochu S, která je zvolenou křivkou l ohraničena.

Užitím Stokesovy věty vektorové analýzy (D 1.45) lze levou stranu rovnice (5.3) vyjádřit rovněž pomocí plošného integrálu. Bude pak platit

.

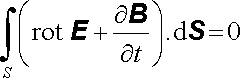(5.4)

Vzhledem k libovolnosti plochy S můžeme vztah (5.4) zapsat též v dife-renciálním tvaru jako

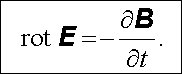(5.5)

Vidíme tedy, že obecně nestacionární elektrické pole není potenciální, a není jej tedy možné ani vyjádřit jako gradient nějakého skalárního pole - potenciálu.

Ve vztahu (5.5) se poprvé setkáváme s diferenciální rovnicí, která vzájemně svazuje vektor intenzity elektrického pole a vektor magnetické indukce. Kdyby­chom nyní přepsali soustavu rovnic pro stacionární, respektive kvazistacionární elektrické a magnetické pole (viz čl. 4.1.3) a nahradili v ní rovnici rot E = 0 vztahem (5.5) , dostali bychom

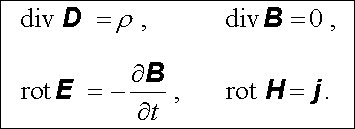(5.6)

Vzniká otázka, nakolik adekvátně popisuje soustava rovnic (5.6) nestacionární, časově obecně proměnné elektromagnetické pole. Pokud jde o rovnici div D = ρ víme, že představuje diferenciální tvar Gaussova zákona, jehož platnost jsme postulovali pro libovolně se pohybující náboje (srov. čl. 2.2.1). Ve shodě s Maxwellem provedeme nyní další zobecnění a budeme požadovat, aby Gaus­sův zákon platil ve stejném tvaru, tj. ve tvaru (1.247) , respektive (1.248) i pro obecně nestacionární elektrické pole.

Požadavek platnosti Gaussova zákona div D = ρ pro nestacionární elektrické pole zahrnuje ovšem nutnost rozlišovat i v tomto obecném případě volné a vá­zané náboje a předpokládat platnost vztahu mezi vektorem elektrické indukce a vektorem elektrické polarizace (1.246)

,

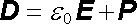který zůstává definičním vztahem vektoru elektrické indukce.

Rovnice div B = 0, kterou zapisujeme v integrálním tvaru jako, viz (3.72) ,

,

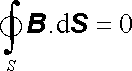vyjadřuje ve stacionárním případě neexistenci magnetických nábojů (srov. čl. 3.3.3). Obecný zákon elektromagnetické indukce však vyžaduje, aby vztah (3.72) zůstal zachován i v nestacionárním případě. Jen tehdy má totiž velikost magnetického indukčního toku plochou ohraničenou danou smyčkou jedno­značný význam. Zobecnění platnosti rovnic div D = ρ a div B = 0 na obecný nestacionární případ je dnes navíc potvrzeno celou dosavadní experimentální zkušeností.

Zbývá zjistit, zda rovnice rot H = j představující diferenciální tvar Amp`erova zákona platí rovněž pro nestacionární pole. Snadno nahlédneme, že tomu tak není. Z této rovnice totiž plyne (viz (D 1.68))

,

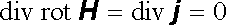(5.7)

zatímco z rovnice kontinuity (3.15) pro nestacionární případ máme

.

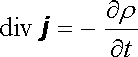Soustava rovnic (5.6) není tedy ještě konečným slovem a nepopisuje úplně ne­stacionární elektromagnetické pole. Zbývá vhodným způsobem zobecnit po­slední z těchto rovnic. Také tento mimořádně hluboký myšlenkový krok provedl Maxwell a ukážeme jej v následujícím článku. "Estetické" neuspokojení se sou­stavou (5.6) vyvolává i její určitá nesymetrie; zatímco rotace intenzity elektric­kého pole závisí na změně magnetické indukce, ve výrazu pro rotaci magnetické indukce se analogický člen neobjevuje.

Experimentální zkušenost ukazuje, že i neúplná soustava (5.6) má své opráv­nění za určitých podmínek, a to pro ne příliš rychle proměnné pole. Je to tedy soustava rovnic pro kvazistacionárni elektromagnetické pole. S kvazistacionár­ním elektrickým polem jsme se již setkali v kapitole 4. Tam jsme jej však chá­pali v poněkud jiném významu. Šlo o elektrické pole vyvolané elektrickými náboji, jejichž rozložení v prostoru je ovlivněno působením elektromagnetické indukce v uzavřených obvodech. Uvedli jsme, že toto elektrické pole je potenci­ální a splňuje rovnici (1.50) . Hovořili jsme též o kvazistacionárním magnetic­kém poli v tom smyslu, že jsme předpokládali platnost Amp`erova zákona (3.138) i pro nepříliš rychle proměnné proudy. Vazba mezi těmito kvazistacio­nárními poli se tedy neprojevila ve formulaci Maxwellových rovnic, ale vý­hradně prostřednictvím indukovaného elektromotorického napětí v obvodu.

Odpoutáme-li se od uzavřeného elektrického obvodu, nabude zákon elektromagnetické indukce diferenciální podoby (5.5) a elektrické pole přestane být potenciálním. Přesný obsah výrazu "kvazistacionární pole" není bohužel ustálen, a je proto třeba vždy blíže vymezit toto pole pomocí příslušných matematických vztahů.

Zobecnění zákona elektromagnetické indukce a jeho vyjádření v diferenciálním tvaru (5.5) umožňuje nový pohled na výsledek experimentu vyloženého na konci článku 4.1.2. Indukovaný elektrický proud ve smyčce obepínající dlouhý solenoid či toroid (viz obr. 4.6) můžeme chápat jako důsledek působení indukovaného elektrického pole E na volné nositele náboje ve vodiči smyčky.

Uvedený experiment dokumentuje, že indukované elektrické pole vzniká i v místech s nulovou magnetickou indukcí. Indukované elektrické pole E má nyní zřejmě význam indukované vtištěné intenzity 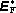, kterou jsme pro popis jevu elektromagnetické indukce fenomenologicky zavedli v článku 4.1.2. Ze srovnání výrazu (4.13) pro indukované elektromotorické napětí s výrazem (3.28) udávajícím obecný vztah mezi elektromotorickým napětím a vtištěnou intenzitou obdržíme pro intenzitu indukovaného elektrického pole vztah

.

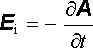(5.8)

Tento výsledek znovu dokumentuje užitečnost vektorového potenciálu pro popis elektromagnetic­kého pole (viz článek 5.1.4).

5.1.2 proudu

Vraťme se nyní k rovnici rot H = j a pokusme se upravit její pravou stranu tak, aby nebyla v rozporu s rovnicí kontinuity. Předpoklad obecné platnosti Gaus­sova zákona div D = ρ umožňuje upravit rovnici kontinuity (3.15) na tvar

.

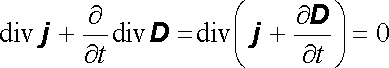Vidíme tedy, že veličina

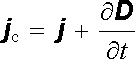(5.9)

splňuje vždy podmínku

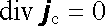(5.10)

podobně jako hustota stacionárního proudu. To přivedlo Maxwella na myšlenku, že touto veličinou je třeba nahradit hustotu volného makroskopického proudu j v Amp`erově zákonu (3.138) rot H = j . Dostáváme tak rovnici

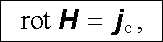(5.11)

popř.

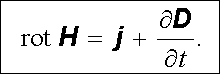(5.12)

Rovnice (5.11) , popř. (5.12) , představují zobecněný Amp`erův zákon v dife-renciálním tvaru. Popisují nestacionární magnetické pole a jejich fyzikální obsah nelze vysvětlit na základě dříve vyložených zákonitostí elektrických a mag-netických jevů. Představují tedy nový fyzikální zákon, jehož platnost, dnes již plně experimentálně potvrzenou, předpověděl právě Maxwell. Zbývá ovšem vyjasnit fyzikální smysl veličin vystupujících v rovnicích (5.11) , popř. (5.12) , a vyjasnit tak fyzikální obsah samotného pojmu nestacionární magnetické pole.

Jelikož stacionární a kvazistacionární magnetické pole jsou speciálními případy obecného pole nestacionárního, je možné považovat za samozřejmé, že i nestacionární magnetické pole se bude projevovat jednak silovými účinky na pohybující se náboje a jednak elektromagnetickou indukcí. Veličinou bezpro­středně vyjadřující oba tyto fyzikální projevy bude opět vektor magnetické in­dukce B . Silové účinky budou vyjádřeny Lorentzovým vzorcem (3.56) , který bude i nadále představovat definiční vztah pro intenzitu elektrického pole E a pro magnetickou indukci B . Zákon elektromagnetické indukce zůstane vyjá-dřen vztahem (5.5) . Pro popis nestacionárního magnetického pole v látkovém prostředí si podrží svůj význam i intenzita magnetického pole H , pro jejíž definici zůstanou zachovány vztahy (3.136)

.

Veličinu j _c můžeme považovat za celkovou hustotu makroskopického nestacio­nárního proudu. Je to obecně časově proměnná veličina, jejíž definiční vztah (5.9) lze užitím (1.246) rozepsat do tvaru

.

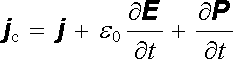(5.13)

Vidíme, že j _c zahrnuje hustotu volného (kondukčního a konvekčního) proudu j , která popisuje transport volných nábojů, dále se v něm objevuje člen ozna-čovaný jako hustota polarizačního proudu (3.12)

,

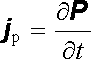který popisuje transport vázaných nábojů v látce při změně její elektrické polari­zace (viz článek 3.1.2) a konečně obsahuje člen

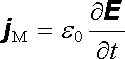(5.14)

nazývaný hustota Maxwellova proudu (někdy také hustota posuvného proudu ve vakuu). Polarizační a Maxwellův proud nazýváme někdy souhrnně posuvným proudem.

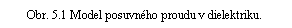
Polarizační proud v dielektriku si můžeme názorně představit jako oscilaci elementárních dipólů (viz obr. 5.1). Uvažme model homogenního dielektrika tvořeného orientovanými elementárními dipóly. Každý takový dipól nechť před­stavuje dvojici opačných bodových nábojů velikosti Q oddělených vzdáleností l, a má tedy dipólový moment o velikosti p = Ql. Nechť vázané, například kladné náboje vykonávají kmitavý pohyb tak, že střídavě protínají myšlenou plochu S a vytvářejí tak makroskopický střídavý proud. Hustotu těchto nábojů označme ρ _p a koncentraci dipólů označme N. Bude-li rychlost pohybu nábojů v _p, dostaneme pro posuvný proud

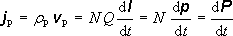. (5.15)

Hustota Maxwellova proudu j _M má skutečně fyzikální rozměr proudové hus­toty. Jde o zvláštní, nový typ proudu, který není přímo spojen s pohybem elek­trických nábojů (!), nýbrž s časovou změnou elektrického pole. Právě tento Max-wellův proud umožňuje uzavřít obvod střídavého proudu, v němž je zapojen kondenzátor s vakuovou mezerou mezi deskami, podobně jako kmity pružné nepropustné membrány v trubici s kapalinou mohou zprostředkovat proměnný tok kapaliny trubicí. Maxwellův proud zřejmě tedy může (a musí) existovat pouze v případě nestacionárního elektrického pole.

Zavedením celkového proudu I_c o hustotě j _c (5.13) můžeme zobecnit i Amp`e­rův zákon (3.137) v integrálním tvaru, na jehož pravé straně je nyní třeba uvažo­vat celkový proud tekoucí plochou ohraničenou křivkou l:

.

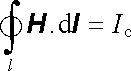(5.16)

V tomto tvaru platí Amp`erův zákon zcela obecně, nezávisle na způsobu rozlo­žení proudu v uvažované ploše a na volbě této plochy. Z tvaru rovnic (5.16) , popř. (5.12) , a z fyzikálního významu veličin I_c a j _c je zároveň vidět fyzi­kální smysl provedeného zobecnění: V nestacionárním magnetickém poli popsa­ném rovnicemi (5.16) , popř. (5.12) , jsou vedle magnetických účinků vol­ných proudů zahrnuty i magnetické účinky polarizačního a Maxwellova proudu. Kvazistacionární magnetické pole, u něhož se magnetické účinky polarizačního a Maxwellova proudu zanedbávají, popisuje správně elektromagnetické jevy jen v situaci, kdy platí

.

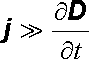(5.17)

Pro elektromagnetické pole ve vakuu platí

(5.18)

dvojice vektorů D , E a B , H se liší pouze konstantami bez fyzikálního obsahu.[35] Rovnice (5.12) může být pak vyjádřena pomocí veličin E , B , popisujících bez­prostředně účinky pole, ve tvaru

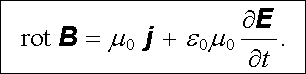(5.19)

Jak se snadno přesvědčíme, veličina 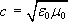má fyzikální rozměr rychlosti. V článku 5.3.1 uvidíme, že na rozdíl od konstant ε ₀ a μ ₀ má c jasný fyzikální význam: představuje totiž rychlost šíření elektromagnetických vln ve vakuu.

5.1.3 rovnic

V předchozích dvou článcích jsme ukázali, jak lze zobecnit rovnice popisující vlastnosti makroskopického elektrického a magnetického pole na případ nestacio­nárního, časově libovolně proměnného pole. Viděli jsme, že v tomto případě elektrické pole závisí vedle rozložení elektrických nábojů též na změnách mag­netického pole a magnetické pole vedle rozložení elektrických proudů také na změnách elektrického pole. To nás opravňuje zavést pojem jediného, a to elektromagnetického pole. Důsledkem tohoto zobecnění je pak předpověď existence elektromagnetických vln, které jsou dnes ve všech svých vlastnostech podrobně experimentálně i teoreticky prozkoumány.

Při odvozování rovnic elektromagnetického pole jsme v celém průběhu vý­kladu postupovali induktivní metodou, tj. vycházeli jsme z experimentálních fakt a pozorování a přecházeli od případů speciálních ke stále obecnějším. Při kaž­dém takovém kroku jsme upozorňovali, že formulaci zákonů a rovnic platných pro případ speciální nelze automaticky přenášet na případ obecnější, i když se to zdá sebevíce "samozřejmé" a zdánlivě není důvodu o obecnější platnosti získa­ných vztahů pochybovat. Každé zobecnění je třeba znovu experimentálně ově­řovat, důsledky z něho plynoucí porovnávat s praktickou zkušeností. Postup, který jsme použili, odpovídá zároveň i historické cestě, na níž byly poznatky o elektromagnetismu v průběhu několika století získávány.

Vlastnosti makroskopického elektromagnetického pole se tak podařilo nako­nec shrnout do čtyř obecně platných fyzikálních zákonů. Jsou jimi zákon Gaussův, zákon Amp`erův zobecněný na případ celkového, nestacionárního proudu, Faradayův zákon elektromagnetické indukce a zákon o neexistenci magnetických nábojů.

Tyto zákony byly formulovány v integrálním tvaru v této podobě:

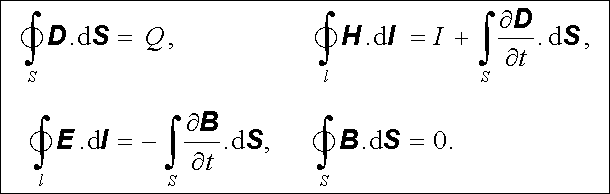(5.20)

Veličina Q značí volný náboj v objemu ohraničeném plochou S, veličina I proud procházející smyčkou l.

V diferenciálním tvaru představují tyto zákony soustavu čtyř parciálních dife­renciálních rovnic, Maxwellových rovnic elektromagnetického pole:

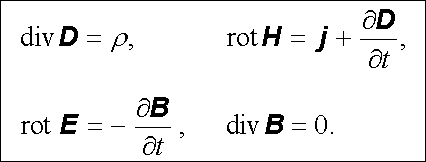(5.21)

Rovnice uvedené v prvním řádku se někdy nazývají první sérií Maxwellových rovnic a udávají vzájemný vztah mezi vektory elektromagnetického pole, obje­movou hustotou volných nábojů ρ a hustotou volných proudů j . Rovnicím v dru­hém řádku se říká druhá série Maxwellových rovnic, vyznačují obecně platné vlastnosti vektoru intenzity elektrického pole E a magnetické indukce B . Všimněte si, že pro vektory D a H takovéto obecné vlastnosti formulovat nelze.

Při formulování soustavy Maxwellových rovnic jsme se omezili na případ elektromagnetického pole v prostředí nacházejícím se v klidu vůči pozorovací soustavě souřadnic. Indukovaná elektromotorická napětí, popř. další jevy vznikající v pohybujících se vodičích, je třeba popsat pomocí dodatečných vněj­ších vtištěných sil. Vyčerpávající popis vlastností makroskopického elektromag­netického pole v pohybujícím se prostředí lze nalézt v učebnicích teorie elek­tromagnetického pole, v nichž jsou uplatněna hlediska teorie relativity (viz například [3]).

Z Maxwellových rovnic vyplývá obecná rovnice kontinuity proudu (3.15) , kterou jsme v článku 3.1.3 formulovali jako výraz obecného zákona zachování náboje. Dostaneme ji po aplikaci operace divergence na rovnici pro rot  H , vyjád­říme-li div  D pomocí hustoty volných nábojů ρ . Tento výsledek nás ovšem ne­překvapuje, neboť jak jsme viděli v předchozím článku, bylo zobecnění rovnice pro rot  H motivováno právě požadavkem platnosti rovnice kontinuity v obecném tvaru.

Maxwellovy rovnice (5.21) představují soustavu parciálních diferenciálních rovnic prvního řádu. Takové rovnice mají nekonečně mnoho různých řešení a k vyčlenění jednoznačného fyzikálního řešení je nutné doplnit hraniční pod­mínky. Pohlížíme-li na soustavu (5.21) jako na rovnice k určení vektorů E , B , D a H při zadaném rozložení volných nábojů a proudů, jde o soustavu lineárních nehomogenních rovnic. Můžeme též řešit opačnou lineární úlohu, zjišťovat ob­jemovou hustotu nábojů a hustotu proudů při zadaném elektromagnetickém poli. Tato úloha, zejména v podobě určování pohybu bodových nábojů v elektrických a magnetických polích, má velký praktický význam v elektronice a budeme se jí zabývat v kapitole 6. Nejobecněji můžeme vzít v úvahu, že náboje a proudy se pohybují vlivem sil elektromagnetického pole, ale zároveň samy toto pole i ovlivňují. Tím vzniká velmi složitá nelineární úloha, která nebyla v celé obec­nosti dosud vyřešena.

Čtyři neznámé vektorové funkce E , B , D , H představují dvanáct neznámých funkcí skalárních a počet osmi (složkových) Maxwellových rovnic je zřejmě k jejich určení nedostatečný. Víme však, že v látkovém prostředí existují materi­álové vztahy. V určité aproximaci mohou být vyjádřeny funkčními závislostmi D  = D ( E ) a B  = B ( H ) . Pro mnoho látek můžeme dokonce předpokládat plat­nost lineárních vztahů

,

(5.22)

a k určení vektorů D a H stačí tedy znát permitivitu ε a permeabilitu μ prostředí. V neizotropních lineárních prostředích, kde vektory E a D , popř. B a H nemusí mít týž směr, je třeba znát složky tenzoru permitivity, resp. permeability. Vztahy (5.22) můžeme v souladu s (1.255) a (3.136) zapsat ve tvaru

,

(5.23)

kde χ _e a χ _m jsou i elektrická a magnetická susceptibilita prostředí.

V kapitole 3 byl prokázán značně obecný charakter Ohmova zákona, viz (3.26) ,

.

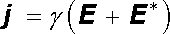Výrazy (5.22) a (3.26) jsou příkladem lineárních materiálových vztahů, které umožňují nahradit údaje o prostorovém rozložení vektorů j , D a H v látkovém prostředí znalostí takzvaných materiálových konstant γ , ε , μ (popřípadě ještě vtištěné intenzity E  ^*).

Doplníme-li soustavu Maxwellových rovnic materiálovými vztahy, zjedno­duší se úloha na hledání vektorů E (r , t) a B (r , t) (tedy šesti skalárních funkcí), jejichž fyzikální význam je dán Lorentzovým vzorcem (3.56) . Ve vakuu, kde nejsou přítomny elektrické náboje a proudy a kde platí ε = ε ₀, μ = μ ₀, nabudou Maxwellovy rovnice zvláště jednoduchého a symetrického tvaru

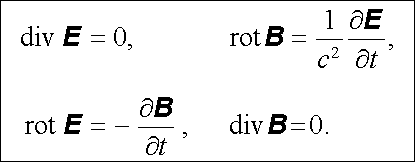(5.24)

Právě vytčený postup lze využít k určení průběhu polí pouze v těch bodech, v jejichž bezprostředním okolí se parametry prostředí mění spojitě. V oblastech, kde dochází k jejich nespojitým změnám (například na plošném rozhraní dvou typů prostředí), však Maxwellovy rovnice v podobě (5.21) selhávají. V těchto případech je třeba průběh pole vyšetřit užitím integrálních vztahů (5.20) . Jak víme, pomocí těchto vztahů byly ve speciálních případech odvozeny podmínky pro změnu tečných, popř. normálových, složek vektorů D , E , B a H při přechodu rozhraním dvou prostředí (1.80) , (1.82) , (3.84) , (3.139) . Protože integrální vztahy pro toky vektorů D a B uzavřenými plochami zůstávají v platnosti i v případě nestacionárního pole, budou z nich odvozené podmínky

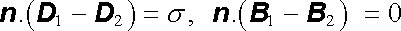(5.25)

také obecně platné. V integrálních vztazích pro cirkulace vektorů E a H podél uzavřených křivek se nyní objevují nové členy s parciálními derivacemi ℜ ∂ B /ℜ ∂ t a ℜ ∂ D /ℜ ∂ t . Provedeme-li však analogické odvození s křivkami tvaru malých ob­délníčků přimykajících k vyšetřované ploše jako v odstavcích 1.2.6 a 3.5.3 a uvážíme-li konečné hodnoty vektorů B a D a jejich derivací, zjistíme, že tyto nové členy výsledek neovlivní. Můžeme tedy opět psát

.

(5.26)

Použijeme-li pojmů plošné divergence a rotace zavedených v dodatku D  l, mů­žeme podmínky na rozhraní vyjádřit v jednoduché a symetrické podobě

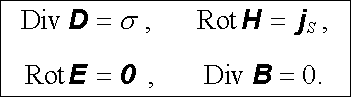(5.27)

Na pravé straně zde přitom vystupují plošná hustota volných nábojů σ a lineární hustota volných plošných proudů j _S. Existují-li v látkovém prostředí (dielektriku či magnetiku) pouze vázané náboje a proudy, budou tyto hustoty ovšem nulové a podmínky na rozhraní se dále zjednoduší.

Z matematického hlediska je třeba vztahy (5.27) považovat za hraniční pod­mínky, kterým musí řešení Maxwellových rovnic (5.21) na plochách nespojitostí vždy vyhovovat. Pro určení konkrétního průběhu elektromagnetického pole dané soustavy mají proto stejnou důležitost jako Maxwellovy rovnice samotné.

5.1.4 Potenciály elektromagnetického pole

V předchozích kapitolách jsme uváděli, že vektorové pole, jehož rotace je v určité oblasti rovna nulovému vektoru, může být vyjádřeno jako gradient něja­kého skalárního pole φ . Tak jsme zavedli například elektrostatický potenciál vztahem (1.50) , ale i magnetostatický potenciál vztahem (3.157) a podobně jsme mohli zavést i potenciál stacionárního elektrického pole. Zavedením skalárního potenciálu jsme zjednodušili výpočet elektrického pole, neboť místo rovnic pro tři složky vektoru intenzity pole stačilo řešit Laplaceovu rovnici (1.86) , popř. Poissonovu rovnici (1.85) , pro jedinou skalární funkci. Podotkněme, že jsme přitom nepřisuzovali hodnotě potenciálu přímý fyzikální smysl a definovali jsme jej nejednoznačně, s přesností na aditivní konstantu.

Naopak pro solenoidální vektorové pole, jehož divergence je rovna nule, jsme v článku 3.3.3 (viz též dodatek D  l) zavedli vektorový potenciál tak, aby zmíněné solenoidální pole bylo rovno rotaci tohoto vektorového potenciálu. Také pomocí vektorového potenciálu jsme zjednodušili výpočet magnetického pole a dospěli opět k vektorové Poissonově rovnici (3.79) . Vektorový potenciál byl definován s přesností na libovolné aditivní pole A splňující podmínku rot  A  = 0 .

Obecné elektromagnetické pole není ani potenciální, ani solenoidální. Vzniká otázka, není-li možné i v tomto případě zavést potenciály pole tak, abychom usnadnili výpočet a hlouběji prozkoumali obecné vlastnosti tohoto pole.

Soustava Maxwellových rovnic (5.21) ukazuje, že vektorové pole B , které je nyní ovšem vázáno s elektrickým polem E , je solenoidální, a můžeme tedy za­vést vektorový potenciál A vztahem B = rot A . Tento vektorový potenciál bude nyní ovšem představovat nestacionární vektorové pole A (r , t). Po jeho dosazení do rovnice pro rot E dostaneme

.

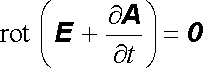(5.28)

I když elektrické pole E není potenciální, ukazuje se být potenciálním pole E + ℜ ∂ A / ℜ ∂ t . Můžeme tedy zavést skalární potenciál φ ( r , t), který bude opět nestacio­nární, vztahem

.

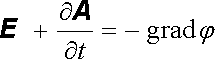(5.29)

Zavedeme-li nyní tyto potenciály do první série Maxwellových rovnic, stačí vyřešit pouze tyto dvě rovnice (jednu vektorovou a jednu skalární) pro potenci­ály a výsledné pole určit ze vztahů

(5.30)

Druhá série Maxwellových rovnic vystupuje tedy pouze jako určitá obecná podmínka kladená na elektromagnetické pole, která bude při tomto postupu spl­něna automaticky. Navíc na oba potenciály φ , A bude možné klást dodatečné požadavky, které nám usnadní nalézt jednoznačného řešení pro pole E a B .

Naznačený postup provedeme za zjednodušujícího předpokladu, že mezi vektory D a E , B a H platí lineární materiálové vztahy (5.22) . Dosazením (5.30) do první série Maxwellových rovnic dostaneme

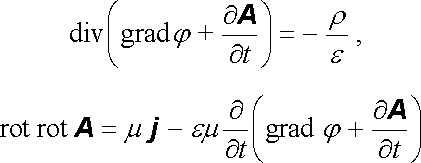(5.31)

a tyto rovnice upravíme pomocí vzorců vektorové analýzy (D.1.56) a (D.1.58) na tvar

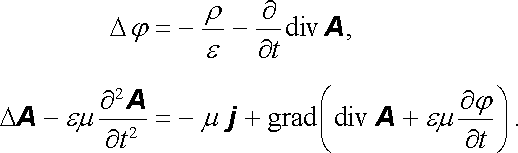(5.32)

Soustava rovnic (5.32) je dosti složitá a zavedením potenciálů jsme si v obecném případě nepomohli. Kdybychom však mohli požadovat, aby potenciály φ , A splňovaly podmínku

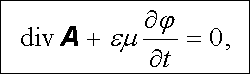(5.33)

odpadne druhý člen na pravé straně druhé z rovnic (5.32) a tyto rovnice se radi­kálně zjednoduší na tvar

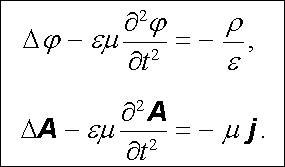(5.34)

Soustava (5.34) představuje čtyři takzvané nehomogenní vlnové rovnice (jednu dvojici rovnic skalární a jednu vektorovou). Metody řešení těchto rovnic jsou podrobně studovány matematickou fyzikou.

Jsou-li v nějaké oblasti prostoru hustota volných nábojů a hustota volných proudů nulové, přejde soustava rovnic (5.34) na rovnice homogenní

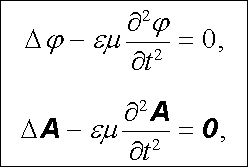(5.35)

které popisují šíření elektromagnetických vln v prostoru. (Tyto rovnice předsta­vují vlastně zobecnění Laplaceových rovnic na nestacionární případ.) Nehomo­genní rovnice (5.34) pak navíc popisují vyzařování a pohlcování těchto vln, které je důsledkem tzv. budicích členů na pravé straně rovnic.

Podmínka (5.33) , kterou jsme omezili potenciály, se nazývá podmínkou Lorentzovou a možnost jejího uplatnění vyjadřuje důležitou vlastnost elektro­magnetického pole. Připomeňme, že ve stacionárním poli přejde tato podmínka v požadavek div  A = 0, který jsme využili v kapitole 3. Elektromagnetické po­tenciály nejsou určeny jednoznačně, a můžeme je proto nahradit novými poten­ciály φ ℜ' , A ℜ' podle vztahů

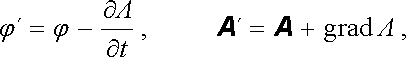(5.36)

kde Λ je libovolná funkce.

Transformace (5.36) se nazývají kalibrační (též cejchovací), protože se při nich nemění měřitelné veličiny E a B . Snadno si ověříme, že podle (5.30) a (D 1.64)

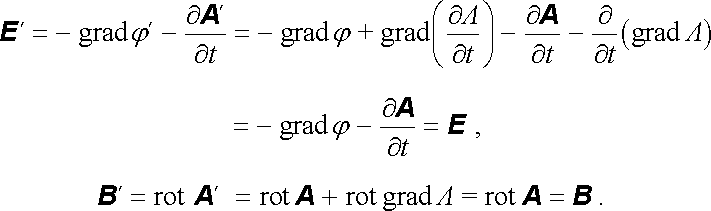(5.37)

Elektromagnetické pole je, jak říkáme, kalibračně invariantní, a tím se řadí k neobyčejně významné třídě polí studovaných ve fyzice elementárních částic.

Uplatníme-li Lorentzovu podmínku na potenciály φ ℜ' , A ℜ' , dostaneme

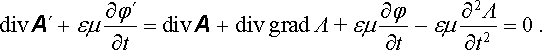(5.38)

Vidíme tedy, že k tomu, abychom mohli řešit Maxwellovy rovnice metodou potenciálů za použití Lorentzovy podmínky, musí existovat řešení nehomogenní vlnové rovnice pro Λ :

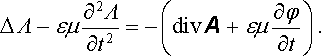(5.39)

Na pravé straně této rovnice vystupuje zadaná funkce souřadnic a času. V matematické fyzice se ukazuje, že tato rovnice má dokonce nekonečně mnoho řešení, a tak je možné vždy příslušnou funkci Λ zvolit a Lorentzovu podmínku použít.

---

---