Při popisu elektromagnetických jevů jsme dosud (s výjimkou kapitoly 2) sledovali makroskopický (fenomenologický) přístup v jeho historické souvislosti a postupně jsme dospěli od polí statických a stacionárních k obecnému poli elektromagnetickému. To je makroskopicky popsáno soustavou Maxwellových rovnic (5.21) shrnujících bohatou experimentální zkušenost. Elektrické a mag-netické pole jsme z počátku zaváděli víceméně formálně jako vhodný prostředek popisu silového působení elektrických nábojů a proudů a teprve obecné ne-stacionární pole charakterizované Maxwellovými rovnicemi se nám ukázalo být zcela reálným fyzikálním objektem. Toto pole souvisí s pohybem elektrických nábojů a proudů, ale může existovat i nezávisle na nich jako elektromagnetická vlna šířící se prostorem.
Je třeba si uvědomit, že Maxwellova teorie vznikala v době, kdy nebylo téměř nic známo o mikrofyzikální struktuře látek. Je proto nutné ji považovat za teorii fenomenologickou, založenou na výsledcích experimentálního studia chování makroskopických objektů. Vliv látkového prostředí na chování elektromagnetického pole je v Maxwellově teorii popsán zavedenými materiálovými konstantami, jako jsou relativní permitivita, relativní permeabilita a konduktivita (měrná vodivost). Maxwellova teorie sama není schopna nic říci o hodnotách těchto konstant ani o jejich závislosti na parametrech elektromagnetického pole či jiných fyzikálních podmínkách. V rámci makroskopické teorie je tedy nutné je určovat experimentálně.
Maxwellova teorie elektromagnetického pole zaznamenala velké úspěchy především předpovědí existence elektromagnetických vln, na jejichž základě bylo možné vypracovat i elektromagnetickou teorii světla. Zároveň však již v posledních desetiletích devatenáctého století byly provedeny některé experimenty, které umožnily vytvoření představ o existenci "elementárních atomových kvant elektřiny". Na základě studia vedení proudu zředěnými plyny byl objeven elektron, čímž byla tato hypotéza potvrzena. Pak již byla zřejmá potřeba nové mikroskopické teorie, která by za prvé byla schopna popisovat elektromagnetické jevy v mikroskopickém měřítku a která by za druhé umožnila kvantitativní výpočet makroskopických materiálových konstant na základě chování mikroskopických objektů - elektronů, atomů, molekul apod.
První mikroskopickou teorii elektromagnetických jevů vytvořil H. A. Lorentz v devadesátých letech devatenáctého století. Výchozím bodem jeho teorie byla v té době již přijímaná představa o atomové struktuře látek. Lorentz předpokládal, že látkové prostředí je složeno z elementárních (mikroskopických) kladných a záporných elektrických nábojů, které jsou zdrojem každého elektromagnetického pole. Lorentz dále předpokládal, že toto pole může být považováno za elektromagnetické pole ve vakuu a může být popsáno odpovídajícími rovnicemi Maxwellova typu.
I když v Lorentzově době nebyla ještě známa struktura atomu a atomového jádra, měla tato teorie značný význam a stala se východiskem pro řešení řady fundamentálních problémů tehdejší fyziky. Jednou z jejích zásluh je samotné vymezení úkolu mikroskopické teorie jako teorie modelové. Elektrický náboj tvořící zdroj elektromagnetického pole je z hlediska této teorie chápán jako jedna z primárních charakteristik jeho mikroskopických nositelů. Chování těchto nositelů je podmíněno jejich fyzikální podstatou a nemůže být odvozeno jen z rovnic elektromagnetického pole. Je-li však vytvořen model postihující některé podstatné stránky chování uvedených objektů, mohou již být rovnice elektromagnetického pole použity nejen k určení tohoto pole, ale také k určení zpětného působení elektromagnetického pole na nositele náboje. Dalším, možná ještě významnějším, přínosem Lorentzovy teorie je, že umožnila hlubší poznání nej-obecnějších vlastností elektromagnetického pole, což nakonec vedlo k vytvoření teorie relativity.
V kapitole 2 jsme viděli, že model bodových (nebo bezstrukturně objemově rozprostřených) nábojů ve vakuu pohybujících se jednoduchým zadaným způsobem, umožňuje na základě Coulombova zákona a relativistických Lorentzových transformací dospět k soustavě rovnic (2.77) , formálně shodné se soustavou Maxwellových rovnic pro D = ε 0 E , B = μ 0 H . Model použitý v kapitole 2 nevyžaduje rozlišování mezi makroskopickým a mikroskopickým přístupem. Naproti tomu z něho ovšem nelze bez dalšího experimentálního nebo teoretického zdůvodnění dělat závěry pro reálné pole v látkovém prostředí.
Základem Lorentzovy mikroskopické teorie je předpoklad, že jediným zdrojem elektromagnetického pole jsou mikrofyzikální částice, které jsou nositeli náboje. Tento předpoklad umožnil popsat libovolné elektromagnetické pole pomocí prostorového rozložení a pohybu těchto elementárních nábojů ve vakuu.
Lorentz předpokládal, že i v mikroskopickém měřítku lze zavést veličinu ρ (m)( r , t) vyjadřující okamžitou hodnotu objemové hustoty náboje v daném bodě. Dále předpokládal, že pohyb mikroskopických nábojů je možné popsat polem rychlosti v (m)( r , t) [40] , takže můžeme zavést hustotu mikroskopického proudu
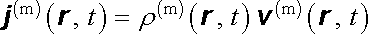 . . |
(5.175) |
Pohybující se elementární náboje vytvářejí podle Lorentzových předpokladů mikroskopická elektromagnetická pole, jejichž vektory e (r , i), d (r , i), b (r, i), h (r , i) jsou s veličinami ρ (m), v (m), j (m) ve vztahu popsaném rovnicemi Max-wellova typu. Podle uvedeného pojetí je možné toto mikroskopické pole po-važovat za pole ve vakuu, takže platí relace d = ε 0 e , b = μ 0 h . Libovolné elektromagnetické pole ve vakuu je možné popsat pouze dvěma vektorovými funkcemi: vektorem intenzity elektrického pole a vektorem magnetické indukce. Odvoláme-li se na soustavu Maxwellových rovnic (5.21) , můžeme rovnice pro mikroskopická pole napsat ve tvaru
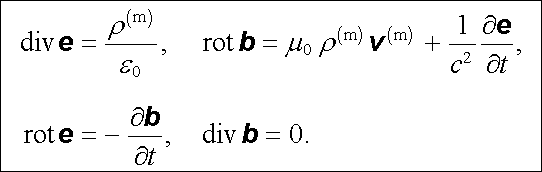 |
(5.176) |
Rovnice (5.176) se nazývají Lorentzovými rovnicemi. Vzhledem k tomu, že popisují pole ve vakuu, jsou formálně poněkud jednodušší než rovnice Maxwellovy a z fyzikálního hlediska obecnější. Lze na ně pohlížet jako na primární, tj. výchozí, a makroskopické Maxwellovy rovnice z nich vyvodit. Elektromagnetické pole popisované Lorentzovými rovnicemi je z fyzikálních důvodů principiálně nestacionární, neboť mikročástice jsou v neustálém komplikovaném pohybu.
Vektory e a b mají v rámci Lorentzovy teorie opět význam veličin popisujících silové účinky na pohybující se mikroskopické náboje. Platí pro ně definiční rovnice analogická s rov. (3.56) ; objemová hustota síly působící na tyto náboje je dána výrazem
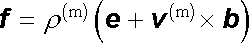 . . |
(5.177) |
Předpoklad o platnosti Lorentzových rovnic (5.176) zahrnuje v sobě i požadavek, aby také v mikroskopickém měřítku platil zákon zachování náboje. Jednoduchým postupem (srov. čl. 5.1.2) dostaneme z (5.176) rovnici kontinuity
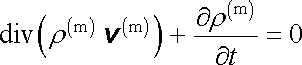 . . |
(5.178) |
Zdůrazněme ještě nakonec, že veličiny e , b , ρ (m), v (m), j (m) vystupující v rovnicích mikroskopického pole mají jiný fyzikální smysl než analogické veličiny E , B , ρ , v , j , se kterými jsme dosud pracovali při vyšetřování makroskopického pole. Například mikroskopická hustota náboje ρ (m) představuje veličinu udávající okamžité rozložení nábojů v prostoru, které je dáno okamžitými polohami jednotlivých mikroskopických nositelů náboje (elektronů, atomových jader apod.). Je zřejmé, že její hodnota se bude měnit o mnoho řádů již v rámci rozměrů jednoho atomu, tj. na vzdálenosti 10-10 m, a dokonce i uvnitř atomového jádra s rozměry 10-15 m. Podobně vektory e a b vyjadřují okamžité hodnoty pole v daném bodě. Pomocí vztahu (5.177) by bylo možné vyjádřit okamžitou hodnotu síly, která by působila na jediný elektron umístěný v libovolném bodě prostoru i uvnitř látkového prostředí. Vektory makroskopických polí E a B takovou možnost nedávají a podobná mikroskopická pole nejsou ani dostupná přímým experimentálním měřením.
Mikroskopická teorie vyjádřená Lorentzovými rovnicemi otevírá ovšem zcela nový obzor, nové otázky a problémy na další strukturní úrovni. Můžeme se ptát na zákonitosti pohybu mikročástic, na možnost existence dalších sil vedle elektromagnetických, působících mezi těmito částicemi, a na jejich možnou souvislost se silami elektromagnetickými, na fyzikální vlastnosti vakua a zda vakuum ovlivňuje pohyb mikročástic a další. Tyto otázky se však již vymykají z rámce klasické fyziky a v Lorentzově době na ně nebylo možné dát odpověď.
Při makroskopickém popisu jevů vždy neuvažujeme diskrétní atomovou strukturu látek. Danou konkrétní látku považujeme za kontinuum a předpokládáme, že veličiny popisující její fyzikální stav se mění spojitě v celém objemu látky. Je pak jasné, že se tyto makroskopické veličiny mění jen nepatrně na vzdálenostech srovnatelných s rozměry atomů či molekul.
Pokud jde o elektromagnetické pole, víme, že k jeho vyčerpávajícímu makroskopickému popisu musíme zavést veličiny E , D , B , H , ρ , j vystupující v Maxwellových rovnicích, které mají uvedené vlastnosti makroskopických veličin. Na druhé straně, za Lorentzova předpokladu, že jediným zdrojem elektromagnetického pole jsou mikrofyzikální částice nesoucí elektrický náboj a jestliže je toto pole správně popsáno mikroskopickými veličinami e , b , ρ (m), v (m), musí mít uvedené makroskopické veličiny význam časových a prostorových středních hodnot příslušných veličin mikroskopických. Kromě toho musí po vystředování z Lorentzových rovnic vyplynout rovnice Maxwellovy.
Ukažme si, že takový postup je skutečně možný. Nejdříve si však všimneme samotného problému výpočtu střední hodnoty libovolné mikroskopické veličiny f (r , t). Abychom vypočítali její prostorovou i časovou střední hodnotu v bodě r (x, y, z) a v okamžiku t, uvažme malý objem Δ V, uvnitř něhož leží bod r, a dále uvažujme malý časový interval Δ τ . Slovo "malý" je třeba chápat ve fyzikálním smyslu - objem V musí být dostatečně malý z makroskopického hlediska (například vzhledem k uvažovaným makroskopickým rozměrům tělesa), ale zároveň dostatečně velký z mikroskopického hlediska (musí obsahovat velký počet mikročástic). Podobně časový interval Δ τ , velmi krátký z makroskopického hlediska, musí být podstatně delší, než je například "perioda oběhu" elektronů v atomu.
Střední hodnotu ℘ ϒ f ℘ ± funkce f v daném bodě r v okamžiku t budeme definovat jako integrál
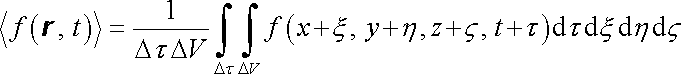 . . |
(5.179) |
Tato střední hodnota nesmí přitom záviset na volbě objemu Δ V a intervalu Δ τ , pokud mají uvedený charakter. Proměnné x, y, z, t vystupují v integrálu (5.179) jako parametry. Budeme vždy předpokládat, že funkce f umožňuje záměnu pořádku derivování podle x, y, z, t a integrování podle &ksi; ,η ,ζ , τ . Potom platí
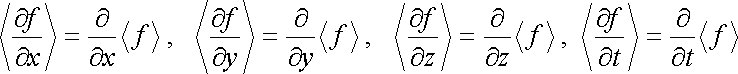 . . |
(5.180) |
Aplikujme nyní proces středování na mikroskopické veličiny vystupující v Lorentzových rovnicích. S ohledem na (5.180) je zřejmé, že střední hodnoty ℘ ϒ e ℘ ± , ℘ ϒ b ℘ ± , ℘ ϒ ρ (m) ℘ ± , ℘ ϒ v (m) ℘ ± budou rovněž vyhovovat Lorentzovým rovnicím
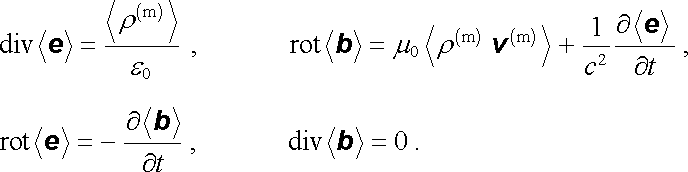 |
(5.181) |
V těchto rovnicích je zřejmě třeba interpretovat střední hodnotu ℘ ϒ e ℘ ± jako intenzitu makroskopického elektrického pole E = ℘ ϒ e ℘ ± a podobně střední hodnotu ℘ ϒ b ℘ ± jako makroskopickou magnetickou indukci B = ℘ ϒ b ℘ ± . Pokud jde o střední hustotu náboje ℘ ϒ ρ (m) ℘ ± , je přirozené chápat ji jako celkovou makroskopickou hustotu náboje v daném bodě. V kapitole l jsme ukázáli, že z makroskopického hlediska je třeba rozlišovat mezi volnými a vázanými náboji. Použijeme-li již zavedeného označení jejich hustot ρ 0 a ρ p můžeme psát
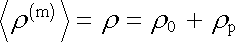 |
(5.182) |
nebo podle (1.168) také
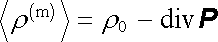 . . |
(5.183) |
Poněkud složitější je otázka interpretace střední hodnoty mikroskopického proudu ℘ ϒ j (m) ℘ ± = ℘ ϒ ρ (m) v (m) ℘ ± . Je samozřejmé, že tato veličina musí v sobě zahrnovat především celkovou hustotu makroskopického proudu v daném bodě, tedy součet hustot kondukčního a konvekčního proudu j a hustoty posuvného (polarizačního) proudu j p. Podrobnější rozbor této otázky však ukazuje,[41] že střední hodnotu nelze redukovat na prostý součet veličin j + j p. Kromě nich je nutné doplnit další člen, který již nevyjadřuje skutečný makroskopický transport náboje. Platí tedy
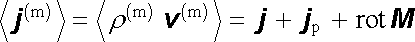 , , |
(5.184) |
kde M představuje makroskopickou magnetizaci látky v daném bodě.
Poslední člen v (5.184) jsme v článku 3.5.2 nazvali hustotou vázaných (magnetizačních) proudů j m. Nyní jsme pomocí Lorentzových rovnic získali konkrétnější představu o jejich významu. Vázané proudy představují střední hodnotu určité části mikroskopických proudů, které se uzavírají v "obvodech" mikroskopických rozměrů - uvnitř jader, atomů, molekul. Přesto, že tato veličina nereprezentuje žádný přenos náboje v makroskopickém měřítku (a v případě takzvaných spinových momentů dokonce ani přenos náboje v prostoru), a nevyjadřuje tudíž ani žádný makroskopický proud, přispívá k hodnotám makroskopického magnetického pole.
Z rovnic (5.181) již velmi snadno obdržíme Maxwellovy rovnice. Stačí dosadit z (5.183) a (5.184) , vzít v úvahu vyjádření polarizačního proudu v dielektriku (3.12)
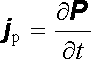 |
a zavést vektor elektrické indukce D a vektor intenzity magnetického pole H pomocí vztahů, viz (3.136) ,
 . . |
Soustavu Maxwellových rovnic (5.21) jsme tedy získali jednak induktivní cestou zobecňování experimentální zkušenosti vyjádřenou v základních zákonech elektromagnetického pole, jednak na základě mikroskopického modelu středováním rovnic Lorentzových. Ovšem i Lorentzovy rovnice se opírají o zmíněnou experimentální zkušenost. Rovněž Maxwellovy rovnice lze odvodit z obecnějších fyzikálních principů, k nimž patří takzvané principy variační, na nichž je dnes založena teoretická fyzika. Tyto principy dovedou popsat z jednotného hlediska jak pohyby částic, tak i vlastnosti pole a jejich vzájemnou interakci. Také tyto obecné principy jsou však výsledkem dlouhé cesty zobecňování experimentálních poznatků a nejsou dány apriorně.
Jakmile dospějeme k matematické formulaci obecných principů nebo rovnic elektromagnetického pole a pohybu částic, můžeme již postupovat deduktivní cestou, matematicky odvozovat další vztahy mezi materiálními objekty (včetně vztahů dosud neznámých) a řešit konkrétní situace při nesčetných aplikacích ve fyzice a v technice. Souhlas těchto konkrétních předpovědí s výsledky experimentu nás stále utvrzuje v přesvědčení o správnosti výchozích předpokladů a rovnic. Případný nesouhlas by ovšem mohl signalizovat neúplnost či nedo-statečnou obecnost výchozích vztahů.
ÚLOHY KE KAPITOLE 5
Ú 5.1: Určete úhlovou frekvenci a polarizaci elektromagnetické vlny, která vznikne jako superpozice dvou monochromatických rovinných vln se stejnými amplitudami a velmi blízkými frekvencemi, jež jsou kruhově polarizovány v opačném smyslu a šíří se jedním směrem. Návod: zvolte osu z jako směr šíření, pak
(eq0214),
Ú 5.2: Silný svazek světla pulsního laseru dopadá kolmo na dokonale absorbující povrch a přenáší výkon o hustotě 1014 W. cm-2. Světelnou vlnu můžeme považovat za rovinnou, harmonickou, lineárně polarizovanou. Určete amplitudu intenzity elektrického pole vlny.
Ú 5.3: Jaká je tloušťka povrchové skinové vrstvy v měděném vodiči pro elektromagnetickou vlnu o vlnové délce l m?
Ú 5.4: Elektromagnetická vlna vyzařovaná elementárním dipólem se šíří ve vakuu. Amplituda intenzity elektrického pole ve vlnové zóně ve směru kolmém k ose dipólu je ve vzdálenosti l m rovna 10 V.m-1. Určete celkový vyzařovaný výkon dipólu I.
Ú
5.5: Relativní permitivita ionosféry
závisí na kmitočtu dopadající elektromag-netické vlny vztahem
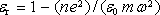 ,
kde n je koncentrace, e náboj a m hmotnost elektronu. Nechť tato vlna dopadá na ionosféru pod úhlem
π
/4.
Určete minimální vlnovou délku pro totální odraz, je-li koncentrace elektronů
v ionosféře 106 cm-3.
,
kde n je koncentrace, e náboj a m hmotnost elektronu. Nechť tato vlna dopadá na ionosféru pod úhlem
π
/4.
Určete minimální vlnovou délku pro totální odraz, je-li koncentrace elektronů
v ionosféře 106 cm-3.
[35] V Gaussově absolutní soustavě jednotek platí pro pole ve vakuu D = E , B = H a všechny čtyři vektory mají týž fyzikální rozměr (viz (D 2.6)).
[36] Mikroskopickým výkladem termodynamických vlastností makroskopických soustav se zabývá statistická fyzika.
[37] Aplikace zákonů termodynamiky na rovnovážné záření vede k požadavku obecné relace mezi intenzitou záření a koeficientem absorpce (tzv. Kirchhoffovy zákony) a k odvození závislosti integrální intenzity na teplotě (Stefanův-Boltzmannův zákon). O těchto otázkách je možné se poučit například v [1]. Experimentálně je možné vliv rovnovážného tepelného záření na vyšetřovanou soustavu vyloučit jejím obklopením tělesem udržovaným na teplotě, která je rovna teplotě soustavy.
[39] Číselně ji určili W. Weber a R. Kohlrausch v roce 1855.
[40] Kvantová mechanika později ukázala, že mechanický pohyb mikročástic nelze popisovat jako pohyb po určitých drahách určitými rychlostmi a že je třeba respektovat vlnový charakter pohybu těchto částic. Pomocí vlnové funkce lze však definovat hustotu pravděpodobnosti výskytu částice v dané oblasti prostoru v daném čase a tímto způsobem zavést mikroskopickou hustotu náboje a proudu. Vlnový charakter pohybu mikročástic je třeba respektovat především tehdy, je-li koncentrace těchto částic vysoká, jako je tomu v pevných látkách. Naproti tomu v plynech, zředěném plazmatu a elektrolytech lze pohyb nositelů náboje studovat z hlediska klasické fyziky.
[41] Středování mikroskopických polí při přechodu k poli makroskopickému představuje dosti složitý problém. V tradiční formě jsou tyto otázky diskutovány například v knize: R. Becker, F. Santer: Theorie der Elektrizität, III. Band, B. G. Teubner, Stuttgart 1968. Velmi podrobná analýza přechodu od mikroskopického k makroskopickému poli, včetně některých modernějších přístupů je uvedena v monografii: S. R. de Groot, L. G. Suttorp: Foundation of Electrodynamics, North-Holland Publ. Comp., Amsterdam 1972, ruský překlad: Nauka, Moskva 1982.