V nauce o vlnění se zavádí pojem postupné rovinné vlny. Tato vlna popisuje takový stav neomezeného spojitého prostředí, kdy hodnota určité veličiny f, vyjadřující lokální vlastnosti tohoto prostředí, závisí na čase t a poloze r podle funkce typu
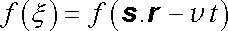 . . |
(5.89) |
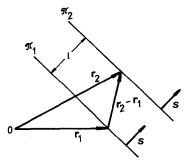
Zde s je jednotkový vektor stálého směru a v značí reálný parametr. Z tvaru funkce (5.89) vyplývá, že v daném okamžiku t má veličina f stejnou hodnotu ve všech bodech roviny π kolmé k vektoru s a dané rovnicí
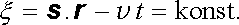 |
(5.90) |
Tato rovina se nazývá rovinou konstantní fáze (rovinnou vlnoplochou); fází rozumíme přitom argument &ksi; funkce f. Parametr v má rozměr rychlosti a nazývá se fázovou rychlostí vlny.
Uvažme dvě různé roviny konstantní fáze π 1 a π 2 dané rovnicí (5.90) a odpovídající dvěma okamžikům t1 a t2. Z obrázku 5.2 je zřejmé, že vzdálenost těchto dvou rovin je rovna
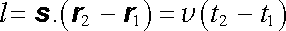 . . |
(5.91) |
Máme tedy rovinnou postupnou vlnu šířící se ve směru vektoru s rychlostí v .
Budeme nyní uvažovat Maxwellovy rovnice pro případ, že celý prostor je vyplněn homogenním nevodivým prostředím o permitivitě ε a permeabilitě μ , ve kterém nejsou přítomny žádné volné náboje. Máme tedy
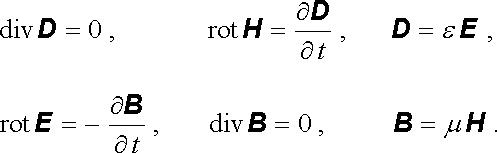 |
(5.92) |
Dvojnásobnou aplikací operace rotace dostaneme po snadné úpravě pro vektory E a B analogické vztahy
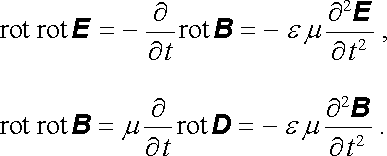 |
(5.93) |
Vzhledem k obecnému vztahu vektorové analýzy (D 1.58) a nulovosti divergence D a B dostaneme z (5.93)
 |
(5.94) |
Všechny složky vektorů E a B vyhovují tedy parciální diferenciální rovnici pro funkci f tvaru
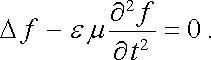 |
(5.95) |
Jak víme, této rovnici vyhovují i potenciály elektromagnetického pole (5.35) . Dosaďme do této rovnice funkci (5.89) , která popisuje šíření postupné rovinné vlny ve směru s . Dostaneme
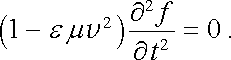 |
(5.96) |
Vidíme tedy, že rovnice (5.95) bude splněna za předpokladu, že fázová rychlost vlny bude rovna
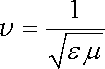 . . |
(5.97) |
Uvedená rovnice představuje homogenní vlnovou rovnici a řešení typu (5.89) je pouze jedním z mnoha řešení této rovnice. Protože jde o rovnici lineární, bude i každá superpozice řešení typu postupných rovinných vln jejím řešením. Rovinná vlna (5.89) představuje tedy důležitý jednoduchý typ vlny, s nímž se setkáváme v mnoha oblastech fyziky a jehož zkoumání umožňuje analyzovat i případy šíření vln složitějšího průběhu.
Složky vektorů E
a B
elektromagnetického
pole se mohou šířit prostorem v podobě rovinné vlny fázovou rychlostí
(5.97)
, která pro případ vakua přechází v rychlost světla ve vakuu c. Možnost existence elektromagnetického
pole šířícího se v podobě vlny v prostoru bez elektrických nábojů vzbuzovala
v Max-wellově době údiv a nedůvěru a teprve objev těchto vln znamenal
velkolepé potvrzení Maxwellovy teorie. Maxwell si rovněž uvědomil, že shoda
konstanty[39]
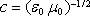 vyplývající z rovnic elektromagnetického
pole, s rychlostí světla ve vakuu není náhodná a vyslovil odtud hypotézu
o elektromagnetické povaze světla. Šíření elektromagnetických vln (světla) v látkovém
prostředí se obvykle charakterizuje (absolutním) indexem lomu n definovaným vztahem
vyplývající z rovnic elektromagnetického
pole, s rychlostí světla ve vakuu není náhodná a vyslovil odtud hypotézu
o elektromagnetické povaze světla. Šíření elektromagnetických vln (světla) v látkovém
prostředí se obvykle charakterizuje (absolutním) indexem lomu n definovaným vztahem
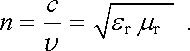 |
(5.98) |
Protože pro většinu látek μ r ℜ ≈ 1, ε r ℜ ≥ 1, je n ℜ ≥ l a elektromagnetické vlny se šíří v látkovém prostředí pomaleji než ve vakuu.
Libovolná dvojice funkcí E ( &ksi; ) , B ( &ksi; ) s &ksi; = s . r - v t nemusí ještě vyhovovat soustavě Maxwellových rovnic (5.92) jako celku. K tomu je třeba, aby ještě splňovaly další podmínky. Abychom tyto podmínky nalezli, uvědomme si, že mezi prostorovými derivacemi a časovou derivací funkce E ( &ksi; ) platí vztahy
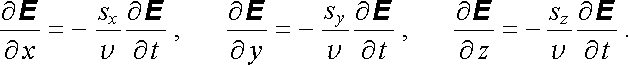 |
(5.99) |
Proto můžeme rotaci E vyjádřit pomocí časové derivace
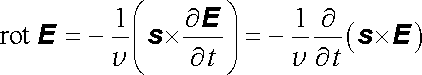 |
(5.100) |
a porovnáním s Maxwellovou rovnicí pro rot E dostaneme
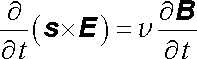 . . |
(5.101) |
Integrací, jestliže položíme integrační konstantu rovnu nule, získáme výsledek
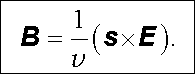 |
(5.102) |
Analogickým postupem lze vypočítat
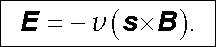 |
(5.103) |
Podmínky (5.102) , (5.103) tedy říkají, že průběh intenzity elektrického pole E a magnetické indukce B ve tvaru rovinné vlny
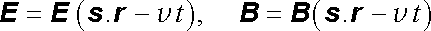 |
(5.104) |
budou řešením Maxwellových rovnic jedině tehdy, budou-li oba vektory v každém okamžiku a každém bodě navzájem kolmé a také kolmé ke společnému směru šíření s . V tomto smyslu je rovinná elektromagnetická vlna příčná, transverzální. Z uvedených podmínek dále vyplývá, že vektory s , E , B tvoří v napsaném pořadí pravotočivý ortogonální systém.
V tomto okamžiku si hloubavý čtenář klade otázku, proč neexistují také rovinné vlny, u nichž by vektory s , E , B tvořily levotočivý systém; jak známo v přírodě se realizují všechny možnosti, které nejsou zakázány některým přírodním zákonem. V daném případě jde však o určité nedo-rozumění způsobené okolností, že vektor magnetické indukce B není polárním vektorem, ale pseudovektorem (viz dodatek D l). Přejdeme-li totiž od pravotočivé kartézské soustavy souřadnic x, y, z k levotočivé pomocí inverze x ℜ → - x, y ℜ → - y, z ℜ → - z, změní vektory E a s znaménko, zatímco pseudovektor B nikoliv. Z trojice vektorů s , E , B se přitom stane levotočivý ortogonální systém. Je zřejmé, že taková změna soustavy souřadnic se nijak neprojeví ve fyzikálních důsledcích a že oba tyto popisy jsou zcela rovnocenné. Přesně vzato bychom neměli znázorňovat pseudovektor B šipkou jako vektor E . Pseudovektor nám udává smysl rotace kolem přímky, ale jeho orientace závisí na tom, zda volíme levotočivou nebo pravotočivou souřadnicovou soustavu. Vidíme tedy, že rovinná elektromagnetická vlna má vektory E a B uspořádány vzhledem ke směru šíření symetricky a nedává možnost jejich alternativního uspořádání.
Velikost vektorů E a B jsou spojeny vztahem
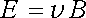 . . |
(5.105) |
Poměr velikostí vektorů intenzity E a H definuje charakteristickou impedanci Z prostředí. Podle (5.105) , (5.97) a materiálových vztahů z (5.92) je
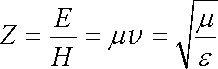 . . |
(5.106) |
Charakteristická impedance vakua je číselně rovna
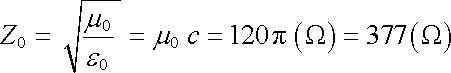 |
(5.106a) |
a velmi málo se liší od charakteristické impedance vzduchu.
Při popisu šíření elektromagnetických vln můžeme tedy vlastnosti prostředí charakterizovat fázovou rychlostí v (respektive indexem lomu n) a chara-kteristickou impedancí Z. Vezmeme-li v úvahu vztah (5.105) , můžeme vyjádřit hustotu energie w a hustotu toku energie S zavedené vztahem (5.48) pro rovinnou vlnu jako
(eq0118),SETEQ(eq0119). (5.107)
Nejčastěji se setkáváme s případem periodických rovinných vln, kdy hodnoty funkce (5.89) se opakují vždy po uplynutí doby T rovné periodě funkce f( &ksi; ) . Veličina
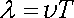 |
(5.108) |
vyjadřující vzdálenost dvou nejbližších vlnoploch, v nichž se funkční hodnota mění synchronně, se nazývá vlnovou délkou. Převrácenou hodnotu periody vlny nazýváme kmitočtem (frekvencí) vlny ν , převrácenou hodnotu vlnové délky vlnočtem σ :
 . . |
(5.109) |
Kmitočet udává počet kmitů za jednotku času, vlnočet počet vln připadajících na jednotku délky.
Podle matematické teorie Fourierovy analýzy (srov. článek 8.3.1) můžeme každou periodickou funkci vyjádřit jako superpozici funkcí harmonických. Za nejjednodušší rovinnou vlnu můžeme tedy považovat takovou, u níž se vektory polí mění podle harmonického zákona:
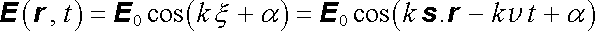 . . |
(5.110) |
Konstantní vektor E 0 představuje amplitudu vlny, veličinu k nazýváme vlnovým číslem (úhlovým vlnočtem), vektor k = k s vlnovým vektorem, veličinu
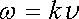 |
(5.111) |
úhlovým kmitočtem (úhlovou frekvencí) a číslo α fázovou konstantou (počáteční fází). V těchto označeních pak můžeme psát
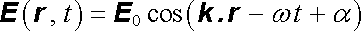 . . |
(5.112) |
Z periodicity harmonické funkce plyne, že úhlový kmitočet souvisí s periodou T a kmitočtem ν vztahem
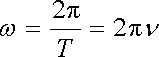 |
(5.113) |
a vlnové číslo s vlnovou délkou λ a vlnočtem σ vztahem
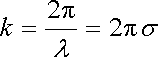 . . |
(5.114) |
Rovnice (5.111) představuje tzv. disperzní vztah pro rovinnou monochromatickou elektromagnetickou vlnu a vyjadřuje souvislost časového a prostorového průběhu vlny. Pro jiné typy vln může disperzní vztah nabývat složitější podoby, zejména může fázová rychlost v =ω /k být funkcí úhlového kmitočtu ω nebo vlnového čísla k. V takových případech mluvíme o časové a prostorové disperzi vlny.
Známe-li průběh intenzity elektrického pole E ( r , t) rovinné harmonické vlny v prostoru a čase, najdeme vektor magnetické indukce B ( r , t) pomocí (5.102) . Dostaneme
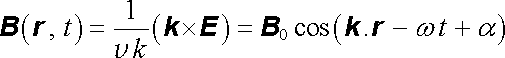 , , |
(5.115) |
kde
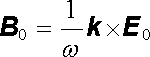 . . |
(5.116) |
Vidíme, že vektor B je zadáním vektoru E plně určen. Elektrické a magnetické pole vlny se mění v každém okamžiku a v každém bodě prostoru s touž fází. Vektory E a B zůstávají navzájem kolmé a společně kolmé ke směru šíření vlny. Situace je znázorněna na obr. 5.3.
Zvolme kartézskou osu z ve směru šíření vlny k . Vektory E a B leží tedy v rovině xy. Při splnění všech dosud odvozených obecných vztahů zůstává ještě neurčitost v poloze vektoru E vůči osám x, y. Není totiž zřejmé, bude-li vektor E při šíření vlny zachovávat svůj směr v prostoru, nebo zda jej bude měnit.
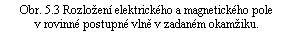
Složky vektoru E do směru os x a y můžeme obecně vyjádřit takto
 . . |
(5.117) |
Ex0
a Ey0 jsou
amplitudy kmitů ve směru souřadných os, α
1
a α
2 obecně
různé fázové konstanty. Označme
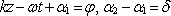 ,
takže
,
takže
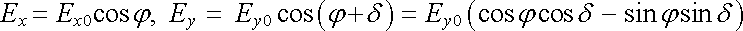 . . |
(5.118) |
Vyjádříme-li z
(5.118)
sin φ
a cos φ
a použijeme-li vztah
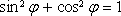 ,
dospějeme k rovnici
,
dospějeme k rovnici
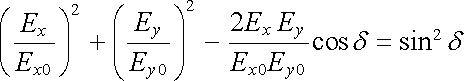 . . |
(5.119) |
Proměnné Ex a Ey nám v této rovnici udávají trajektorii pohybu koncového bodu vektoru E v rovině xy. Rovnice (5.119) představuje přitom rovnici elipsy se středem v počátku souřadnic. Plyne odtud, že monochromatická vlna je obecně elipticky polarizována. Bude-li δ = nπ , kde n je celé číslo, přejde (5.119) na
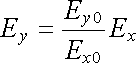 . . |
(5.120) |
V tom případě bude vektor E
oscilovat podél přímky
daného směru vzhledem k osám souřadnic. Říkáme, že taková vlna je lineárně polarizována. Bude-li
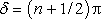 ,
dostaneme
,
dostaneme
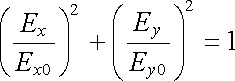 . . |
(5.121) |
Bude-li navíc Ex0 = Ey0 , bude koncový bod vektoru E opisovat kružnici a vlna bude kruhově polarizována. Může být přitom jak pravotočivá, tak levotočivá.
K vyzařování elektromagnetických vln dochází při nestacionárním pohybu elektrických nábojů. Z matematického hlediska bychom přitom museli řešit nehomogenní vlnové rovnice typu (5.34) , což představuje poměrně obtížnou úlohu. Naznačíme proto jen některé vlastnosti nejjednoduššího z takových řešení, dipólového záření ve vlnové zóně.
Vraťme se k článku 1.3.2, kde jsme pomocí multipólového rozvoje hledali elektrostatický potenciál náboje rozloženého v objemu V, a to ve vzdálenostech R značně převyšujících rozměry objemu V. Uvažujme opět takový objem a před-pokládejme, že náboje se v tomto objemu pohybují, takže objemová hustota náboje i proudová hustota jsou nestacionární: ρ (r , t), j (r , t). Nechť je pro jednoduchost celkový náboj v objemu V nulový:
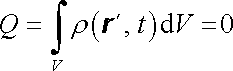 . . |
(5.122) |
Víme, že pro statický náboj bude potenciál dán výrazem
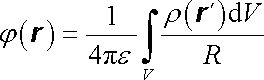 , , |
(5.123) |
kde R = r - r ´, r je polohový vektor bodu, v němž potenciál určujeme, a r ´ probíhá objem V. Analýza nehomogenní vlnové rovnice ukazuje, že i pro nestacionární pole bude skalární potenciál podobného tvaru s tím rozdílem, že při integrování je třeba uvažovat časovou závislost ρ v retardovaném čase tℜ' = t - (R/v ). S retardovaným časem jsme se již setkali v článku 2.2.4 v souvislosti s Liénardovými-Wiechertovými potenciály a jeho zavedení je logický důsledek konečné rychlosti šíření elektromagnetického pole. Máme tedy
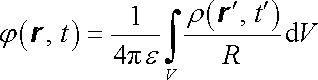 . . |
(5.124) |
Omezíme se opět na přiblížení velkých vzdáleností. Rozvineme-li integrand v (5.124) do Taylorova rozvoje a ponecháme jen členy nejnižších řádů, dostaneme
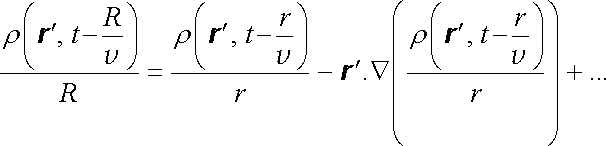 |
(5.125) |
Označme proměnnou t - r/v = τ . Potenciál je pak možné aproximovat jako
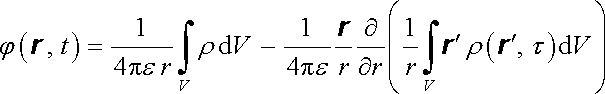 . . |
(5.126) |
První člen na pravé straně (5.126) je podle (5.122) roven nule, druhý můžeme vyjádřit pomocí proměnného dipólového momentu soustavy
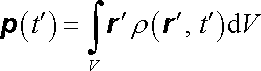 . . |
(5.127) |
Dostáváme tedy skalární potenciál v dipólovém přiblížení
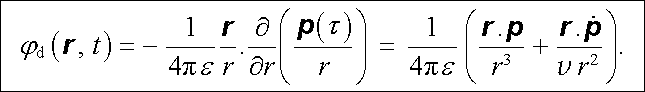 |
(5.128) |
Tečkou jsme označili derivaci p podle celého argumentu t ℜ' = t - R/v , derivace se bere v okamžiku τ . Potenciál (5.128) je možné interpretovat jako retardovaný potenciál buzený časově proměnným dipólem p (t) umístěným v počátku. Vidíme, že první člen (5.128) je formálně shodný s elektrostatickým potenciálem (1.121) .
Nestacionární elektromagnetické pole určujeme ze skalárního a vektorového potenciálu podle vztahů (5.30) . Je tedy ještě třeba znát vektorový potenciál A v odpovídajícím přiblížení. Také vektorový potenciál je třeba určovat integrací proudové hustoty v retardovaném čase. Podle (3.80) máme
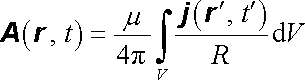 . . |
(5.129) |
V dipólovém přiblížení dostáváme člen
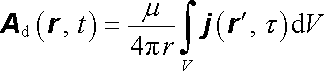 . . |
(5.130) |
V případě stacionárního pole, kdy platí div j = 0 a všechny proudové smyčky musí být v objemu V uzavřeny, bude integrál na pravé straně (5.130) roven nule. V nestacionárním poli však existuje posuvný proud, který v objemu V vyrovnává časové změny rozložení náboje proměnného elektrického dipólu. Použijeme-li výraz pro hustotu posuvného proudu (3.12) , dostaneme
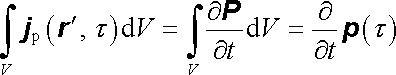 . . |
(5.131) |
Můžeme tedy napsat vektorový potenciál (5.130) ve tvaru
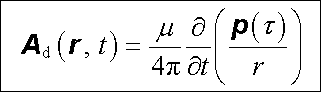 |
(5.132) |
a porovnat jej se skalárním potenciálem (5.128) . V prvním, dipólovém přiblížení popisují potenciály φ d a A d vyzařování elektromagnetického pole soustavou nábojů uzavřených v objemu V a charakterizovaných proměnným dipólovým momentem p (t) . Takovým systémem je například anténa.
Vektory elektrického a magnetického pole najdeme z potenciálů φ d a A d pomocí vztahů (5.30) . Výpočet není principiálně obtížný, ale je pracný. Uvedeme tedy pouze výsledek, přičemž se omezíme na členy úměrné první mocnině 1/r, které převažují v dostatečné vzdálenosti od počátku. Tuto oblast nazýváme vlnovou zónou a je v ní splněna podmínka r >> λ , kde λ je vlnová délka. Vektory E a B jsou zde
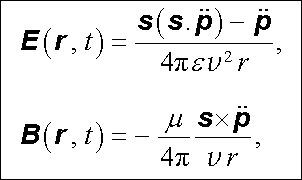 |
(5.133) |
kde s = r /r je jednotkový vektor ve směru r .
Elektromagnetické pole ve vlnové zóně má tvar rozbíhavé kulové (sférické) vlny, neboť plochy konstantní fáze vyhovují rovnici
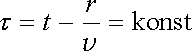 |
(5.134) |
a jsou to kulové plochy rozpínající se fázovou rychlostí v .
Ve vlnové zóně má pole podobné vlastnosti jako rovinná vlna. Je příčné vzhledem ke směru šíření s (snadno si ověříme, že s . E = 0, s . B = 0) a platí pro ně
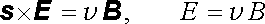 . . |
(5.135) |
Vzájemná poloha vektorů s , E , B je znázorněna na obr. 5.4.

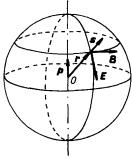
Vidíme, že k vyzařování elektromagnetických
vln do prostoru dochází tehdy, je-li druhá derivace časově proměnného
elektrického dipólového momentu p
nenulová. Směr vektoru p
určuje také charakter
polarizace vlny. Protože je pole E
kolmé ke směru s
, je možné ho vyjádřit
pomocí složky
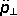 ,
tedy projekce vektoru
,
tedy projekce vektoru
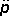 do roviny tečné k vlnoploše:
do roviny tečné k vlnoploše:
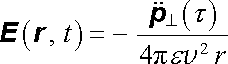 . . |
(5.136) |
Hustota toku energie ve vlnové zóně je podle (5.48) , (5.106) a (5.135)
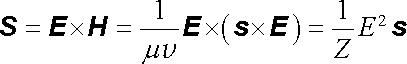 . . |
(5.137) |
Tok energie tedy míří směrem s , jeho hustota má velikost
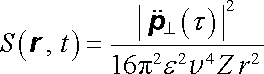 |
(5.138) |
a klesá se čtvercem vzdálenosti. Energie procházející každým okamžikem kulovou plochou o velkém poloměru r nezávisí tedy na r. Tato energie generovaná dipólem p je elektromagnetickým polem unášena nenávratně pryč. Právě takové pole nazýváme elektromagnetickým zářením.
Nyní budeme poněkud konkretizovat časový průběh změny elektrického dipólu, Nechť je tento dipól lineárně polarizován (má konstantní směr p 0, jímž proložíme osu z) a mění se v čase podle harmonického zákona
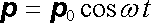 . . |
(5.139) |
Potom
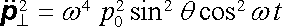 , , |
(5.140) |
kde θ je úhel mezi vektory p 0 a s . Poyntingův vektor dostáváme jako
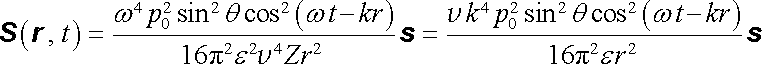 . . |
(5.141) |
Jeho časově střední hodnota je rovna
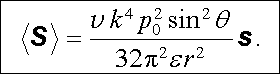 |
(5.142) |
Absolutní hodnotu ℘ ϒ S ℘ ± nazýváme intenzitou záření I( θ ) v daném směru a její úhlové rozložení je vyjádřeno vyzařovacím diagramem (viz obr. 5.5). Dipól vyzařuje s maximální intenzitou ve směru θ = π /2 , zatímco ve směrech θ = 0, π je intenzita záření nulová.
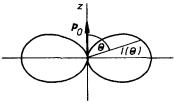
Celkový časově střední výkon vyzařovaný dipólem do prostoru najdeme integrováním intenzity záření I( θ ) ve sférických souřadnicích r, φ , θ přes celý prostorový úhel 4π :
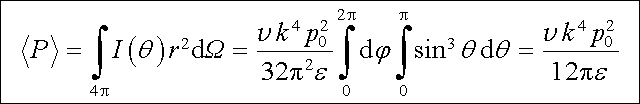 |
(5.143) |
(platí
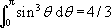 ).
).
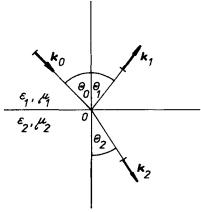
a) Odraz a lom elektromagnetických vln
Nechť monochromatická lineárně polarizovaná rovinná elektromagnetická vlna dopadá na rozhraní dvou nevodivých prostředí charakterizovaných materiálovými konstantami ε 1, μ 1 a ε 2, μ 2 či indexy lomu n1, n2. Označme vlnové vektory dopadající, odražené a lomené vlny k 0, k 1, k 2, rovinu určenou normálou k rozhraní n a vektorem k 0 nazvěme rovinou dopadu. Z důvodu symetrie je zřejmé, že všechny tři vlny budou rovinné a že i vektory k 1 a k 2 budou ležet v rovině dopadu (viz obr. 5.6).
Tečné složky elektrického pole na rozhraní musí být spojité, takže pro libovolné t a r musí pro body rozhraní platit
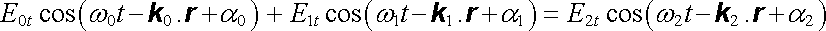 . . |
(5.144)

Podmínku (5.144) nelze splnit jinak, než když
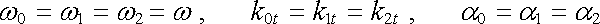 , , |
(5.145) |
takže
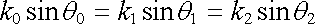 . . |
(5.146) |
Odtud s použitím disperzních vztahů
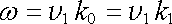 |
(5.147) |
plyne zákon odrazu
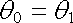 |
(5.148) |
a Snellův zákon lomu
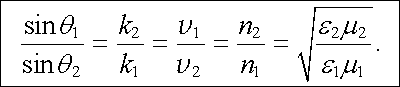 |
(5.149) |
Podmínky na rozhraní umožňují určit také vzájemný poměr amplitud dopadající, odražené a lomené vlny. Z (1.277) a (3.139) pro vektory amplitud plyne
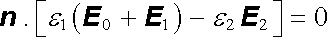 , , |
(5.150a) |
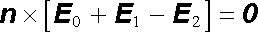 , , |
(5.150b) |
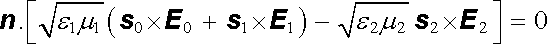 , , |
(5.150c) |
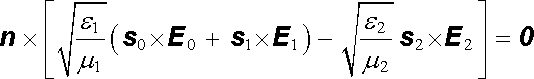 , , |
(5.150d) |
kde
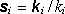 .
.
Zkoumejme nyní zvlášť případ dopadající vlny polarizované kolmo k rovině dopadu a polarizované v rovině dopadu. V prvním případě je podmínka (5.150a) splněna identicky a z (5.150b) plyne
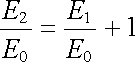 . . |
(5.151) |
Ze
(5.150c)
plyne táž rovnice a
(5.150d)
nám po úpravě a
s uvážením
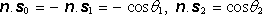 dá
dá
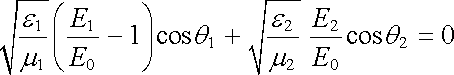 . . |
(5.152) |
Řešením soustavy rovnic (5.151) a (5.152) dostaneme poměry amplitud E1/E0, E2/E0. V elektrických prostředích můžeme aproximovat μ 1 = μ 2 = μ 0, a výsledek se tím podstatně zjednoduší. Dostaneme vztahy
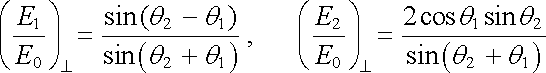 . . |
(5.153) |
Obdobný výpočet pro vlnu polarizovanou v rovině dopadu nebudeme provádět (viz např. [6]), dostali bychom
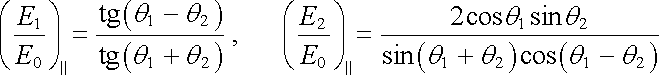 . . |
(5.154) |
Výrazy (5.153) a (5.154) se nazývají Fresnelovy vzorce. Při kolmém dopadu plyne z (5.153) i z (5.154) , tedy bez ohledu na polarizaci vlny,
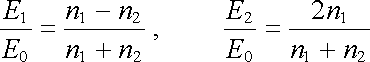 . . |
(5.155) |
V praxi se obyčejně používá jak koeficient odrazu R, tak i koeficient propustnosti T úměrný čtverci amplitud. Tak pro koeficienty odrazu vlny polarizované kolmo a tečně k rovině dopadu podle (5.153) a (5.154) máme
(eq0179)SETEQ(eq0180). (5.156)
Pro koeficienty
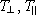 platí, že
platí, že
 .
.
Ze vzorců
(5.156)
plynou zajímavé fyzikální důsledky. Bude-li θ
1
+ θ
2 = π
/2,
potom
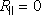 a tečně polarizovaná vlna bude procházet
rozhraním bez odrazu. Podle zákona
(5.149)
to nastane při úhlu dopadu θ
0 =
θ
B , pro
nějž platí
a tečně polarizovaná vlna bude procházet
rozhraním bez odrazu. Podle zákona
(5.149)
to nastane při úhlu dopadu θ
0 =
θ
B , pro
nějž platí
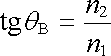 . . |
(5.157) |
Úhlu θ B se říká Brewsterův úhel.
Bude-li θ 2 ℜ ≥ π /2, dojde k totálnímu odrazu vlny na rozhraní. Pro mezní úhel θ 0 = θ T dostáváme
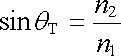 . . |
(5.158) |
Vidíme, že k totálnímu odrazu může dojít jen při přechodu z prostředí o větším indexu lomu do prostředí s menším indexem lomu, a to při libovolné polarizaci vlny.
b) Tlak záření
Při studiu vlastností elektromagnetického pole jsme zjistili, že tomuto poli přísluší objemová hustota energie w a hustota hybnosti g daná podle (5.71) a (5.107) jako
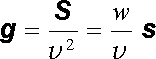 . . |
(5.159) |
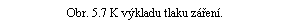
Uvažujme elektromagnetické záření, které dopadá kolmo na povrch látkového tělesa, v němž se toto záření zcela pohltí. Přitom záření odevzdá za dobu Δ t na části povrchu tělesa Δ S hybnost obsaženou v objemu Δ V = v Δ t Δ S (viz obr. 5.7). Tato hybnost je rovna
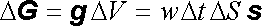 . . |
(5.160) |
Odpovídající síla působící na těleso je
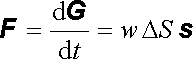 |
(5.161) |
a záření tedy vyvíjí na jednotku plochy povrchu tělesa tlak rovný hustotě energie rovinné vlny w.
Je-li povrch tělesa dokonale odrazivý, změní se hybnost záření při odrazu na opačnou a tlak se zdvojnásobí. Je-li koeficient odrazu povrchu R, bude tento tlak roven (l + R) w.
Experimentální důkaz existence tlaku světla podal P. N. Lebeděv v r. 1899. Tlak záření běžných světelných zdrojů představuje ovšem nesmírně malou veličinu a jeho měření je mimořádně obtížné. Sluneční záření dopadající na povrch Země přináší výkon o plošné hustotě kolem l kilowattu na čtvereční metr, což odpovídá tlaku 3.10-6 Pa. Naproti tomu současné výkonné lasery jsou schopny vyvinout okamžitou plošnou hustotu výkonu až 1019 wattů na čtvereční metr, a tedy tlak záření 3.1010 Pa!
c) Povrchový jev (skinefekt)
Dosud jsme uvažovali pouze o šíření elektromagnetických vln v nevodivém prostředí. Má-li prostředí nenulovou vodivost γ , můžeme zapsat Maxwellovu rovnici pro rot H s užitím Ohmova zákona j = γ E jako
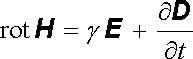 . . |
(5.162) |
Použijeme-li tuto rovnici v soustavě Maxwellových rovnic (5.92) , dostaneme analogickým postupem místo rovnic (5.94) pro vektory E a B rovnice typu
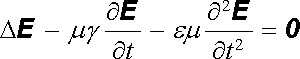 . . |
(5.163) |
Rovnice (5.163) se nazývá zobecněná vlnová rovnice a na rozdíl od vlnových rovnic (5.94) popisuje šíření tlumené elektromagnetické vlny. Vzhledem k vo-divosti prostředí mění se část energie vlny v Jouleovo teplo a amplituda vlny postupně slábne.
Pro velmi dobré vodiče a nepříliš vysoké kmitočty (ω << γ ε ) můžeme v rovnici (5.162) zanedbat posuvný proud. Potom z rovnic
 |
(5.164) |
s uvážením toho, že uvnitř vodiče div E = 0, dostaneme
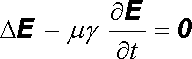 . . |
(5.165) |
Má-li vlna v čase harmonický průběh, můžeme položit
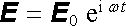 |
(5.166) |
a po dosazení do (5.165) získáme rovnici pro časově nezávislý vektor E 0
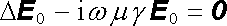 . . |
(5.167) |
Nechť se pole šíří ve směru osy z a vektor E 0 míří podél osy x. Pak z (5.167) máme obyčejnou diferenciální rovnici 2. řádu
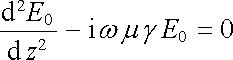 |
(5.168) |
s řešením
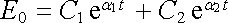 , , |
(5.169) |
kde
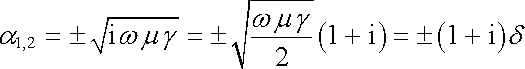 . . |
(5.170) |
Je tedy
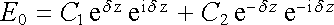 . . |
(5.171) |
Aby pole nenarůstalo do nekonečna, musíme položit C1 = 0 a z (5.166) a (5.171) máme
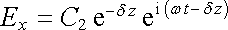 . . |
(5.172) |
To odpovídá proudové hustotě
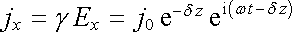 . . |
(5.173) |
Získané výsledky lze jednoduše aplikovat ve dvou situacích. Při kolmém dopadu elektromagnetické monochromatické rovinné vlny na hranici poloprostoru zaplněného vodivým prostředím bude složka elektrického pole rovnoběžná s rozhraním při pronikání do vodiče zmenšovat svou amplitudu s koeficientem útlumu
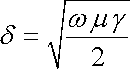 . . |
(5.174) |
Za druhé při protékání střídavého elektrického proudu vodičem v kvazistacionárním přiblížení bude velikost proudové hustoty (5.173) klesat exponenciálně v závislosti na vzdálenosti od povrchu vodiče. Převážná část proudu poteče tedy v povrchové vrstvě tloušťky 1/δ . Jde o takzvaný povrchový jev (skinefekt, z angl. skin = kůže) a projevuje se tím výrazněji, čím vyšší je kmitočet pole (v rámci použitého přiblížení) a vodivost vodiče.