Již v článku 4.1.1 bylo poukázáno na skutečnost, že v elektrických obvodech, ve kterých může docházet ke změnám proudu, existují složitější poměry než v obvodech stacionárních. Příčinou této situace je především jev elektromagnetické indukce, neboť při změnách proudu může v obvodu vznikat indukované elektromotorické napětí, které ovlivní proud tekoucí obvodem. Další rozdíly ve srovnání se stacionárním obvodem přináší uplatnění kapacit mezi jednotlivými vodiči. Uvedená komplikace je způsobena tím, že při změnách potenciálu vodičů dochází ke změnám v rozložení nábojů, a tudíž ke vzniku dodatečných proudů v jednotlivých částech obvodu.
Uvedené okolnosti nejsou samozřejmě zahrnuty ve vztazích, které byly pro stacionární obvod odvozeny v oddílu 3.2. Pro kvazistacionární obvod je třeba tyto vztahy zobecnit a kromě toho je třeba zobecnit i sám pojem elektrického obvodu, což je úkolem tohoto oddílu.
Uvažujme soustavu N vodivých, uzavřených smyček a předpokládejme, že v každé z nich mohou působit obecně časově proměnné vtištěné síly, jejichž vliv v i-té smyčce lze popsat výsledným, obecně časově proměnným elektromotorickým napětím E i(t) . Změny proudu v jednotlivých smyčkách budou dále v každé smyčce indukovat elektromotorické napětí E F,i(t) dané vztahem (4.18) . Doplněním tohoto napětí do rovnice (3.30) , vyjadřující Ohmův zákon pro uzavřený obvod, dostaneme v případě i-té smyčky podmínku
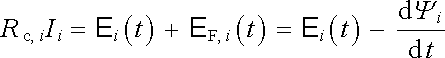 , , |
(4.34a) |
popř.
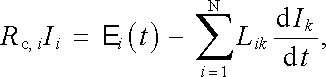 |
(4.34b) |
v níž Rc,i představuje celkový odpor této smyčky a Ii její proud. Ve speciálním případě jediné smyčky se soustava (4.34) zjednoduší na jedinou rovnici
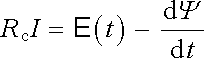 , , |
(4.35a) |
popř.
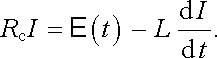 |
(4.35b) |
Rovnice (4.34) , popř. (4.35) , zřejmě nahrazují rovnici (3.30) pro náš obecnější případ, kdy se uplatní vliv jevu elektromagnetické indukce. Je z nich možné vypočítat proudy ve všech smyčkách I1(t), I2(t),..., IN(t) , jsou-li zadána vnější elektromotorická napětí E 1(t), E 2(t),..., E N(t) , celkové odpory Rc,1, Rc,2,..., Rc,N a vlastní i vzájemné indukčnosti Lik. (Jelikož jde o diferen-ciální rovnice prvního řádu, je pro určení konkrétního průběhu proudu třeba ještě znát počáteční podmínky, tj. například hodnotu proudu v určitém okamžiku.) Tyto rovnice však ještě nevystihují situaci v obvodech s proměnným proudem úplně. Není v nich totiž počítáno s vlivem kapacity mezi jednotlivými vodiči.
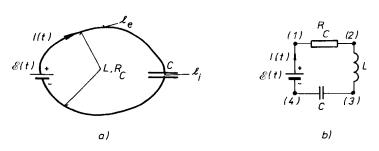
Obr. 4.11 Vodivá smyčka v kvazistacionárním přiblížení: a) realizace smyčky s odporem, indukčnosti a kapacitou, b) schéma smyčky v aproximaci soustředěných parametrů.
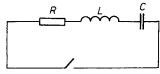
Abychom její vliv mohli poznat, uvažujme jednoduchý obvod podle obr. 4.11a. Předpokládejme, že tento obvod vznikl přerušením vodivého uzavřeného obvodu o celkovém odporu Rc a vlastní indukčnosti Lik, přičemž do místa přerušení byl zařazen kondenzátor kapacity C. Kapacity mezi jednotlivými částmi vodičů původního obvodu zatím zanedbáme, takže vlastnosti nové soustavy budou plně určeny veličinami Rc, L, C. Je samozřejmé, že takto upraveným "obvodem" již nemůže téci stacionární proud. Jeho vodiči však může protékat časově proměnný kondukční proud při změnách náboje na elektrodách kondenzátoru.
Předpokládejme dále, že ve vodičích obvodu působí vtištěné síly, jejichž vliv je možné popsat elektromotorickým napětím E (t) . Provedeme integraci Ohmova zákona (3.26) podél uzavřené křivky l, jejíž část le vedená vně kondenzátoru splývá s vodiči obvodu. Druhá část li, probíhající vnitřkem kondenzátoru, nechť je vedena libovolně. Budeme však předpokládat, že kondenzátor je malých rozměrů, takže bude le >> li, a uvedená libovůle příliš neovlivní velikost plochy ohraničené křivkou l. Pro integrál přes le dostaneme
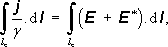
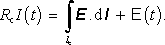
Tyto rovnice však ještě nezahrnují uplatnění indukovaného elektromotorického napětí. Po opravě ve smyslu (4.35a) , resp. (4.35b) bude platit
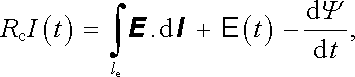 |
(4.36a) |
popř.
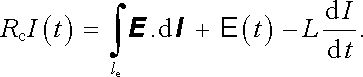 |
(4.36b) |
Rovnici (4.36) můžeme dát jasnější smysl, využijeme-li vlastnosti elektrického pole. Podle článku 4.1.3 víme, že kvazistacionární elektrické pole je potenciální. Pro jeho intenzitu E (r , t) bude tedy v každém okamžiku platit
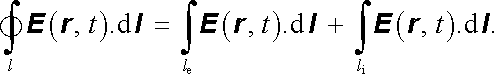 |
Veličina
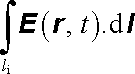 |
však představuje rozdíl elektrického potenciálu (tj. okamžitou hodnotu napětí) UC(t) mezi elektrodami kondenzátoru, který lze užitím (1.201) vyjádřit pomocí kapacity C a okamžité hodnoty náboje na kondenzátoru. Tedy
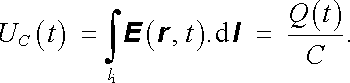 |
(4.37) |
Po dosazení do (4.36) dostaneme pro náš obvod rovnici
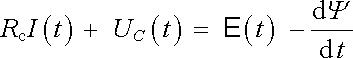 |
(4.38) |
nebo
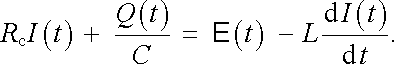 |
(4.38a) |
Rovnice (4.38) a (4.38a) mají pro obvod znázorněný na obr. 4.11a stejný význam jako rovnice (3.30) pro stacionární vodivě uzavřený obvod. Je z nich možno vypočítat proud, známe-li parametry E (t), Rc , L, C (a počáteční podmínky). Podobně jako v případě (4.34) a (4.35) mohou být i tyto rovnice převedeny na tvar lineární diferenciální rovnice (tentokrát druhého řádu), v nichž neznámou veličinou je proud jako funkce času. Uvědomíme-li si, že platí, viz (3.2) ,
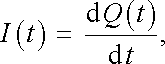 |
dostaneme po zderivování rovnic (4.38)
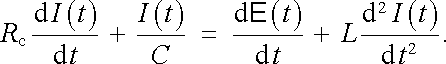 |
(4.39) |
Právě provedená úvaha ukazuje, za jakých podmínek může vodiči spojenými s elektrodami kondenzátoru protékat proud. Při působení časově proměnných elektromotorických napětí je nutné tyto vodiče (spolu s připojeným kondenzátorem) považovat za součást uvažovaných obvodů přesto, že nereprezentují elektricky vodivé spoje. Je tedy zřejmé, že v kvazistacionárním přiblížení je užitečné zobecnit pojem elektrického obvodu. V tomto zobecněném pojetí je třeba za elektrický obvod považovat libovolné spojení (homogenních i nehomogenních) vodičů, které je charakterizováno jejich odpory, elektromotorickými napětími, vlastními i vzájemnými indukčnostmi a také kapacitami mezi jednotlivými částmi vodičů.
Z rovnic (4.34) až (4.39) a také z rovnice kontinuity vyplývá, že v daném okamžiku je proud v každém průřezu nerozvětvené části vodiče stejný. Pro výpočet proudů a napětí na těchto úsecích není proto zapotřebí uvažovat skutečný tvar těchto vodičů. Ke zjednodušení úvah o kvazistacionárních obvodech se proto zavádí tzv. přiblížení soustředěných parametrů. Předpokládáme, že vlastní indukčnosti vodičů lze reprezentovat cívkami velmi malých rozměrů zhotovenými z ideálních vodičů, přičemž jednotlivým dvojicím cívek připisujeme odpovídající hodnoty vzájemných indukčností. Podobně kapacity mezi jednotlivými vodiči nahrazujeme kondenzátory, a o odporech předpokládáme, že jsou soustředěny do velmi malých úseků vodičů, které tvoří prvky nazývané rezistory. Libovolný obvod pak můžeme reprezentovat určitým spojením těchto základních prvků (zdrojů, cívek, kondenzátorů a rezistorů). O vodičích, které je propojují předpokládáme, že jsou ideální; jejich odpory, indukčnosti i kapacity mezi nimi již považujeme za nulové. Uvažovaný obvod podle obr. 4.11a může pak být při využití smluvených schematických značek překreslen do tvaru který, vidíme na obr. 4.11b.
Pro právě zavedený kvazistacionární obvod se soustředěnými parametry lze v podstatě reprodukovat úvahy článku 3.2.4 a odvodit Kirchhoffova pravidla.
Platnost I. Kirchhoffova pravidla ve tvaru uvedeném v čl. 3.2.4 je pro libovolný uzel a v každém okamžiku zřejmá, neboť pro kvazistacionární přiblížení požadujeme platnost rovnice kontinuity ve tvaru (3.16) (viz článek 4.1.3). Slovně může být jeho obsah vyjádřen takto:
Algebraický součet proudů přitékajících do uzlu musí být v každém okamžiku nulový.
Pokud jde o II. Kirchhoffovo pravidlo, je zřejmé, že na libovolnou smyčku v libovolně rozvětveném obvodu lze aplikovat stejný postup, který jsme použili v předchozí části tohoto článku k vyšetřování nerozvětveného obvodu. Dostali bychom výsledek:
Součet napětí na všech odporech a kondenzátorech ve smyčce je v každém okamžiku roven součtu elektromotorických napětí působících ve smyčce a elektromotorických napětí indukovaných ve všech cívkách podél smyčky.
Rovnice (4.34) až (4.39) , které vyjadřují toto tvrzení, je možné též považovat za vyjádření II. Kirchhoffova pravidla pro speciální případy uvažovaných nerozvětvených obvodů.
Při důsledné aplikaci přiblížení soustředěných parametrů můžeme zavést pojmy okamžitých napětí na jednotlivých prvcích obvodu, tj. na jednotlivých odporech, kapacitách a vlastních i vzájemných indukčnostech. Okamžitá hodnota napětí UR(t) odporu R je zřejmě dána Ohmovým zákonem, okamžitá hodnota napětí UC(t) na kondenzátoru C je dána vztahem (4.37) . Tedy
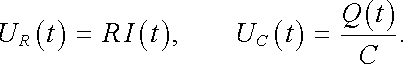 |
Okamžitou hodnotu napětí UL(t) na indukčnosti L lze zřejmě definovat vztahem
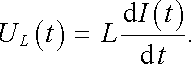 |
(4.40) |
Podle této definice UL(t) představuje okamžitou hodnotu rozdílu potenciálu na svorkách indukčnosti. (Například pro indukčnost L v obvodu znázorněném na obr. 4.11b jde o rozdíl potenciálu mezi svorkami (2) a (3), který je kladný, jestliže proud tekoucí v naznačeném směru vzrůstá.)
Využitím uvedených pojmů lze rovnici (4.38) také vyjádřit ve tvaru
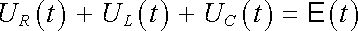 |
(4.38b) |
a II. Kirchhoffovo pravidlo slovně formulovat rovněž takto:
Součet napětí na všech odporech, kapacitách a indukčnostech zařazených do uzavřené smyčky je v každém okamžiku roven součtu elektromotorických napětí působících ve smyčce.
Rozdíl mezi rovnicemi (4.38) a (4.38b) je ovšem jen formální. Obě mohou být převedeny na rovnici druhého řádu typu (4.39) , v níž proud I(t) představuje neznámou hledanou funkci.
Viděli jsme, že zatímco aplikace Kirchhoffových pravidel na stacionární obvody vede obecně na lineární algebraické rovnice pro neznámé veličiny, v případě kvazistacionárních obvodů máme v podobné situaci co činit s lineárními diferenciálními rovnicemi (prvního či druhého řádu). Přesto jsou obecné metody řešení stacionárních a kvazistacionárních obvodů v mnohém podobné. (O obecných metodách řešení elektrických obvodů bude pojednáno v kapitole 8.) V následujících článcích tohoto oddílu probereme ještě některé speciální typy kvazistacionárních obvodů, důležité z praktického hlediska.
Zdrojem střídavého harmonického elektromotorického napětí nazýváme takové zařízení, které produkuje elektromotorické napětí, jehož časová závislost je dána vztahem
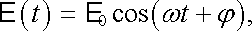 |
(4.41) |
v němž E 0 je amplituda napětí, ω jeho úhlová frekvence a φ fázová konstanta. Probereme dva nejdůležitější principy, které se v technice ke generaci střídavých harmonických elektromotorických napětí užívají.
 První
způsob, užívaný zejména v energetice, pracuje na principu elektrického
generátoru a využívá jevu elektromagnetické indukce ve vodičích pohybujících se
v magnetickém poli (srov. odst. 4.1.2b). Pro demonstraci principu činnosti
uvažujme nejdříve rovinnou cívku o N
závitech rotující v homogenním magnetickém poli B
konstantní úhlovou
frekvencí ω
kolem osy kolmé k ose souměrnosti cívky a ke směru magnetického pole (viz obr.
4.12a). Magnetický tok Φ
průřezem cívky S
bude záviset na čase podle vztahu
První
způsob, užívaný zejména v energetice, pracuje na principu elektrického
generátoru a využívá jevu elektromagnetické indukce ve vodičích pohybujících se
v magnetickém poli (srov. odst. 4.1.2b). Pro demonstraci principu činnosti
uvažujme nejdříve rovinnou cívku o N
závitech rotující v homogenním magnetickém poli B
konstantní úhlovou
frekvencí ω
kolem osy kolmé k ose souměrnosti cívky a ke směru magnetického pole (viz obr.
4.12a). Magnetický tok Φ
průřezem cívky S
bude záviset na čase podle vztahu
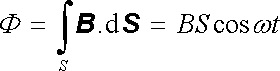 |
a v cívce se indukuje elektromotorické napětí
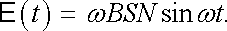 |
(4.42) |
Označením E 0 = ω BSN a vhodnou volbou fázové konstanty φ (tj. vhodnou volbou počátku odečítání času) je můžeme vyjádřit ve tvaru (4.41) .
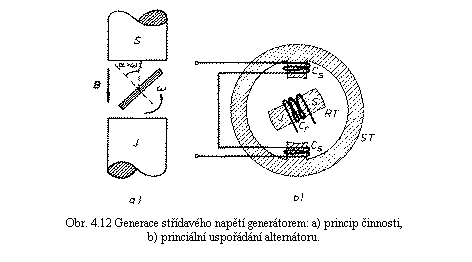
Z praktického hlediska je výhodnější konstrukce, kdy se střídavé elektromotorické napětí indukuje v nehybné cívce. Princip takového uspořádání, nazývaného alternátor, je uveden na obr. 4.12b. Sestává z tzv. statoru ST a rotoru RT. Stator je zhotoven z magneticky měkkého feromagnetika, na jehož pólových nástavcích tvořících plášť válcové dutiny je navinuta cívka Cs snímající indukované napětí. V dutině se pak otáčí magnet (nejčastěji elektromagnet buzený cívkou Cr), který v magnetickém obvodu statoru budí střídavý magnetický tok. Vhodnou konstrukcí tvaru pólů lze zajistit, že se ve statorové cívce indukuje elektromotorické napětí, jehož průběh je s dostatečnou přesností dán vztahem (4.41) .
V silnoproudé elektrotechnice se zpravidla užívají tzv. vícefázové (nejčastěji třífázové) soustavy, které spočívají ve vhodném propojení příslušného počtu zdrojů se synchronně proměnným a vzájemně fázově posunutým elektromotorickým napětím do jednoho systému (n-fázovou soustavu napětí lze například získat pomocí jediného 2n-pólového alternátoru). Podrobněji se otázkami vícefázových soustav ani technickými náležitostmi konstrukce generátorů v této knize zabývat nebudeme a odkazujeme na doporučenou literaturu - např. [9].
Druhý způsob generace střídavého harmonického napětí využívá vlastních kmitů v obvodu s indukčností, odporem a kapacitou. Uvažujme obvod podle obr. 4.13 a předpokládejme, že ve výchozím okamžiku t = 0, kdy zapneme spínač, je kondenzátor C nabit na napětí UC,0. Po zapnutí spínače se kondenzátor počne vybíjet přes odpor R a indukčnost L, takže obvodem poteče proud I(t) . Protože v obvodu nepůsobí žádné elektromotorické napětí, bude možné jej popsat rovnicemi (4.38) až (4.39) , ve kterých položíme E (t) = 0. Speciálně z (4.39) dostaneme pro proud I rovnici
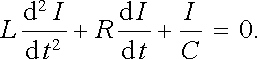 |
(4.43) |
Její obecné řešení má tvar
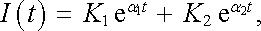 |
(4.44) |
kde K1, K2 jsou integrační konstanty a
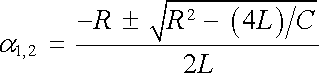 |
jsou kořeny charakteristické kvadratické rovnice.

Řešení
(4.44)
rovnice
(4.43)
má jak známo různý charakter v závislosti na hodnotě
diskriminantu D = R2 - (4L)/C. Pro D ℜ ≥
0
jsou α
1,
α
2
reálné. Proud pak má průběh, který je kvalitativně zobrazen na obr. 4.14. Tento
případ, který vyjadřuje tzv. aperiodický
stav obvodu, nás však nyní nebude zajímat. Obrátíme pozornost ke zbylé
možnosti D < 0. Zavedeme-li, jak je zvykem, reálné
veličiny
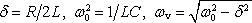 ,
dostaneme α
1,2 = -δ
+/- iω
v. Pomocí nových integračních konstant K,
φ
můžeme pak řešení
(4.44)
psát ve tvaru
,
dostaneme α
1,2 = -δ
+/- iω
v. Pomocí nových integračních konstant K,
φ
můžeme pak řešení
(4.44)
psát ve tvaru
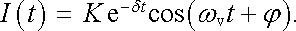 |
(4.45) |
Výsledek
(4.45)
ukazuje, že proud v obvodu může mít
charakter tlumených harmonických kmitů, které nazýváme vlastními kmity obvodu. Veličina δ
zřejmě charakterizuje
rychlost jejich tlumení, a nazývá se proto konstantou
útlumu; za dobu t = 1/δ
poklesne amplituda kmitů e-krát. Na hodnotě konstanty útlumu ovšem také závisí
kruhová frekvence vlastních kmitů
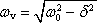 .
.
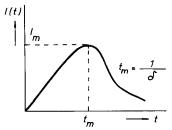
Uplatníme nyní v obecném řešení (4.45) předpokládané počáteční podmínky, které lze vyjádřit vztahy I(0) = 0, UC,0 + L(dI/dt )t = 0 = 0. Těmto počátečním podmínkám vyhovuje například hodnota fázové konstanty φ = -π /2. Pro konstantu K dostaneme K = UC,0/(ω vL), takže z (4.45) obdržíme průběh proudu
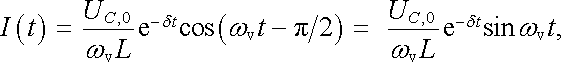 |
(4.46) |
který je kvalitativně zobrazen na obr. 4.15. Pomocí tohoto vztahu je možné snadno kvalitativně diskutovat děje probíhající v obvodu. Kondenzátor, který je ve výchozím stavu nabitý na napětí UC,0, se počne po zapojení spínače vybíjet a proud tekoucí obvodem rychle vzrůstá. S postupujícím vybíjením kondenzátoru klesá energie jeho elektrického pole a současně vzrůstá energie magnetického pole cívky. Po uplynutí čtvrtiny periody proud dosáhne maximální hodnoty. Kondenzátor je téměř vybitý a téměř všechna energie obvodu je soustředěna v magnetickém poli cívky. Jelikož je v tomto stavu dI/dt = 0, je napětí na cívce nulové. Od tohoto okamžiku počne proud klesat, čímž se v cívce indukuje elektromotorické napětí, které postupně nabíjí kondenzátor na opačnou polaritu. Po uplynutí poloviny periody je proud v obvodu nulový a všechna energie je opět soustředěna v elektrickém poli kondenzátoru. Kondenzátor se počne opět vybíjet a celý děj se opakuje.
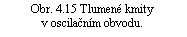
Vlastní kmity v obvodu jsou tedy podmíněny střídavou proměnou elektrického pole v magnetické a naopak. Současně ovšem dochází ke ztrátám v důsledku přeměny části energie v Jouleovo teplo, čímž postupně klesá amplituda kmitů. Tento pokles je samozřejmě tím pomalejší, čím menší je činitel tlumení δ . V praxi užívaných obvodech je často možné dosáhnout stav malého tlumení, kdy δ << ω 0. Vlastní kmity pak mají kruhovou frekvenci ω v = ω 0 závislou jen na indukčnosti a kapacitě, která je dána vztahem
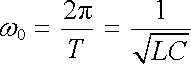 , , |
(4.47) |
jemuž někdy říkáme Thomsonův vzorec. Doba jejich trvání v obvodu může být mnohonásobně delší než perioda T.
Obvod R, L, C s malým tlumením, ve kterém mohou vznikat vlastní tlumené kmity, se nazývá oscilačním obvodem. Je možné doplnit takový obvod přídavným zařízením, které vhodným způsobem doplňuje ztráty energie, takže se v obvodu udržují trvale netlumené kmity. (Vhodným energeticky aktivním zařízením tohoto druhu může být například elektronka či tranzistor.) Obvod s netlumenými kmity může pak být například prostřednictvím vzájemné indukčnosti vázán s jinými obvody a může v nich budit harmonicky proměnné proudy. Z hlediska těchto sekundárních obvodů může být oscilační obvod považován za zdroj elektromotorického napětí E (t) , které lze popsat vztahem (4.41) .
Zdroje střídavého elektromotorického napětí harmonického průběhu představují patrně nejvíce užívaný typ zdrojů ve všech odvětvích elektrotechniky. Díky tomu mají také velký význam střídavé obvody. Rozumíme jimi libovolné spojení rezistorů, cívek a kondenzátorů, které je připojeno ke zdrojům střídavého elektromotorického napětí, nebo jsou v něm generovány střídavé proudy.
Střídavé obvody jsou speciálním případem kvazistacionárních obvodů. Platí pro ně tedy všechny zákonitosti odvozené v předchozím článku. Vzhledem k harmonickému průběhu elektromotorického napětí je však možné je vyjádřit v mnohem konkrétnějším a jednodušším tvaru. Tuto situaci budeme demonstrovat na jednoduchém, avšak dosti obecném a charakteristickém příkladu. Předpokládejme, že ke zdroji střídavého elektromotorického napětí (4.41) je připojena libovolná kombinace rezistorů, cívek a kondenzátorů, jejichž parametry jsou konstantní, nezávislé na protékajícím proudu (tj. vylučujeme např. cívky s feromagnetickými jádry). Z uvažovaného zdroje bude do obvodu dodáván obecně časově proměnný proud I(t) , pro který je možné užitím Kirchhoffových pravidel (viz čl. 4.2.1) sestavit příslušné diferenciální rovnice. Rozborem charakteru těchto rovnic (srov. článek 4.2.4) lze vždy ukázat, že za dostatečně dlouhou dobu po připojení zdroje bude mít proud I(t) protékající jednotlivými prvky harmonický průběh
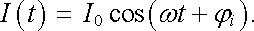 |
(4.48) |
Jeho amplituda I0 bude závislá jednak na amplitudě elektromotorického napětí, jednak na parametrech uvažovaného spojení a na frekvenci ω . Podobný charakter bude mít okamžitá hodnota napětí na daném prvku
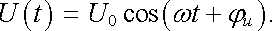 |
(4.49) |
Pro poměr amplitudy napětí a proudu na daném prvku (či na uvažované kombinaci několika prvků) je možné vždy psát
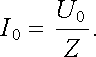 |
(4.50) |
Veličina Z je pro uvažované spojení prvků (rezistorů, cívek, kondenzátorů) charakteristická, závisí obecně na frekvenci a nazývá se impedancí tohoto spojení. Vztah (4.50) definující impedanci, je formálně shodný se vztahem (3.19) vyjadřujícím integrální tvar Ohmova zákona. Je proto možné ji považovat za veličinu v jistém smyslu analogickou odporu vodiče (její jednotkou je rovněž ohm). Je však nutné si uvědomit, že impedance ve smyslu vztahu (4.50) udává pouze relaci mezi amplitudami napětí a proudu. Souvislost mezi fázovými konstantami φ i, φ u je nutné určit z jiných parametrů obvodu.
Stav střídavého obvodu za dobu dostatečně dlouhou po zapnutí příslušných zdrojů elektromotorického napětí, kdy platí vztahy (4.48) až (4.50) a kdy je tedy možné zavést impedanci jednotlivých prvků, se nazývá ustáleným stavem. V opačném případě mluvíme o stavu neustáleném.[33] V článku 4.2.4 budou uvedeny příklady řešení střídavých obvodů v ustáleném i neustáleném stavu. V kapitole 8 pak bude podán systematický výklad metod řešení obecných střídavých obvodů v ustáleném stavu.
Dvojice elektrických obvodů vázaných vzájemnou indukčností představuje další, v praxi velmi důležitý typ kvazistacionárních obvodů. Abychom poznali jejich vlastnosti, uvažujme nejdříve obecnou dvojici uzavřených vodivých smyček podle obr. 4.16a o vlastních indukčnostech L1, L2 a odporech R1, R2. V první (primární) smyčce nechť působí obecně časově proměnný zdroj elektromotorického napětí E 1(t) a mezi oběma smyčkami nechť je vzájemná indukčnost L12. V přiblížení soustředěných parametrů, diskutovaném v článku 4.2.1, může být vyšetřovaná soustava znázorněna schématem, jež vidíme na obr. 4.16b.
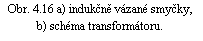
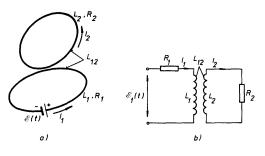
Podle II. Kirchhoffova pravidla platí pro oba obvody rovnice
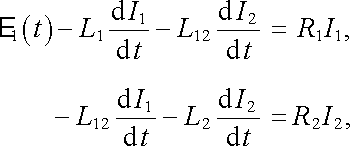 |
(4.51) |
ze kterých lze při známých počátečních podmínkách (a ovšem i všech parametrech obvodů) vypočítat časový průběh proudů I1 i I2. Některé důležité závěry lze však z rovnic (4.51) získat i bez konkrétní znalosti průběhu E 1(t) .
Všimněme si nejdříve situace, kdy je druhá (sekundární) smyčka rozpojena. Mezi konci jejích vodičů lze pak naměřit elektromotorické napětí E 20 = L 12 (dI1/dt) . Bude-li odpor R1 dostatečně malý tak, že bude možné člen na pravé straně první rovnice (4.51) považovat přibližně za nulový, dostaneme
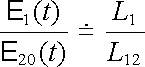 . . |
(4.52) |
Velmi zajímavá je dále otázka, jak se proud sekundární smyčky projeví na chování smyčky primární. Tuto otázku je možné snadno a velmi názorně vyřešit ve speciální situaci, kdy je odpor R2 dostatečně malý tak, že můžeme v každém okamžiku pravou stranu druhé rovnice (4.51) přibližně položit rovnou nule. Platí pak
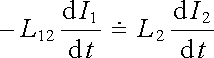 . . |
Po integraci (za předpokladu, že v čase t = 0, kdy byl do primárního obvodu zapojen zdroj, byly oba proudy nulové) dostaneme mezi proudy I1(t) a I2(t) v libovolném okamžiku vztah
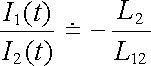 . . |
(4.53) |
Pomocí tohoto výsledku dostaneme z druhé rovnice (4.51)
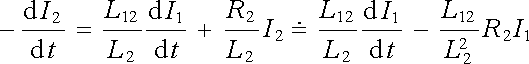 |
a po dosazení do rovnice první
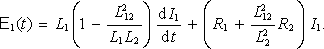 (4.54)
(4.54)
Z výsledku (4.54) plynou dva důležité závěry. Za prvé srovnáním s rovnicí (4.35) a s dynamickým definičním vztahem vlastní indukčnosti (4.17) vidíme, že se primární smyčka chová tak, jako kdyby měla efektivní indukčnost
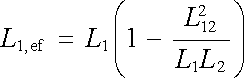 . . |
(4.55) |
Podobně jako pro libovolnou vlastní indukčnost musí i zde
platit L1,ef ℜ ≥
0 (viz úloha Ú 4.5). Přítomnost sekundární
uzavřené smyčky tedy zmenšuje efektivní indukčnost smyčky primární. Obvykle se
zavádí činitel vazby
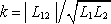 . Lze tedy psát
. Lze tedy psát
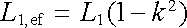 , , |
(4.56) |
přičemž
k ℜ ≤
1.
V mezním případě k = 1 je efektivní indukčnost primární smyčky
nulová. Tento stav těsné vazby, kdy by oběma smyčkami protékal stejný magnetický
tok, nelze ovšem ve skutečnosti dosáhnout; obě smyčky by se musely geometricky
ztotožnit. Pro reálné obvody proto vždy platí k < 1,
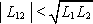 .
(srov.
příklad 4.1.5d), i když hodnoty k
blízké jedné může být vhodnou konstrukcí dosaženo.
.
(srov.
příklad 4.1.5d), i když hodnoty k
blízké jedné může být vhodnou konstrukcí dosaženo.
Ze srovnání výsledku
(4.54)
s rovnicí
(4.35)
pro osamocenou smyčku plyne i druhý závěr. Kromě zmenšení
indukčnosti na efektivní hodnotu L1,ef
se přítomnost sekundárního obvodu projeví také vzrůstem
efektivního odporu primárního obvodu o hodnotu
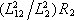 . To odpovídá skutečnosti, že zdroj v
primárním obvodu musí rovněž dodávat energii spotřebovanou při průchodu proudu
sekundárním obvodem na Jouleovo teplo.
. To odpovídá skutečnosti, že zdroj v
primárním obvodu musí rovněž dodávat energii spotřebovanou při průchodu proudu
sekundárním obvodem na Jouleovo teplo.
Soustava induktivně vázaných cívek konstruovaná pro různé obvody v jednotlivých odvětvích elektrotechniky se nazývá transformátor. Obecně může transformátor sestávat z více než dvou cívek s různými činiteli vzájemné vazby, v závislosti na účelu použití. Často je však žádoucí dosáhnout co nejtěsnější vazbu; v ideálním případě k = l mluvíme o ideálním transformátoru.
Pro dosažení maximální těsné vazby dvou cívek je nutné, aby plochami všech jejích závitů procházel společný magnetický tok. Relativně těsné vazby se například dosahuje mezi dvěma válcovými cívkami navinutými z tenkého vodiče těsně na společné kostře (viz 4.1.5e) nebo mezi podobně navinutými toroidními cívkami (srov. úlohu Ú 4.9). Vedle co nejtěsnější geometrie je možné činitele vazby zvýšit navinutím cívek na společné jádro zhotovené z materiálu o vysoké relativní permitivitě r >> 1 tak, aby tvořilo uzavřený magnetický obvod o co nejmenším magnetickém odporu (srov. čl. 3.5.5). Magnetický tok společný induktivně vázaným cívkám se pak uzavírá především tímto jádrem a těsná geometrie cívek přestává mít prvořadou důležitost. Na obrázku 4.17 jsou schematicky zobrazeny dvě nejužívanější konstrukce transformátorů. V případě obrázku 4.17a tvoří jádro jednoduchý magnetický obvod obdélníkového profilu, jímž se uzavírá magnetický tok. Primární a sekundární cívky jsou odděleně navinuty na protilehlých stranách jádra. U transformátoru podle obr. 4.17b jsou primární i sekundární cívky postupně navinuty na středním sloupku jádra. Společný magnetický tok procházející tímto sloupkem se pak uzavírá obvodem jádra, jak je na obrázku naznačeno.
Jádra transformátorů se zhotovují z magneticky uspořádaných feromagnetických či ferimagnetických materiálů (viz články 3.5.4 a 7.2.3). Vedle základního požadavku vysoké relativní permeability jsou na ně kladeny ještě požadavky další. Za prvé jde o to, že při změnách proudu v cívkách transformátoru se materiál jádra přemagnetovává, což je spojeno s přeměnou energie magnetického pole v teplo (srov. příklad 4.3.4b). Tyto procesy, označované jako hysterezní ztráty, jsou ovšem v transformátoru nežádoucí a je třeba je minimalizovat. Jádra transformátorů se tudíž zhotovují z magneticky měkkých materiálů s nízkým koercitivním polem.
Další faktor ovlivňující vlastnosti jádra transformátoru jsou tzv. vířivé (někdy též Foucaultovy) proudy. Tyto proudy jsou důsledkem zákona elektromagnetické indukce a indukují se v elektricky vodivém prostředí vždy, dochází-li v něm k časovým změnám magnetického pole.[34] V trans-formátorech se vířivé proudy projevují nežádoucím způsobem, je-li materiálem jádra elektricky vodivé kovové feromagnetikum. Elektricky vodivé jádro představuje totiž další vodivou smyčku induktivně vázanou s cívkami transformátoru. V důsledku indukovaných vířivých proudů vzniká v jádru Jouleovo teplo, pro něž je potřebná energie dodávána zdroji elektromotorického napětí působícími v obvodu transformátoru (srov. vztah (4.54) ). Pro konstrukci jader je proto třeba volit materiály s co nejnižší elektrickou vodivostí a uspořádat geometrii způsobem, který by velikost vířivých proudů omezil. Klasickým materiálem je magneticky měkká ocel s příměsí křemíku, který snižuje její měrnou vodivost. Další omezení vířivých proudů se dosahuje tím, že se potřebný průřez jádra skládá z tenkých, vzájemně elektricky izolovaných plechů.

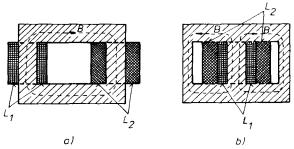
Pro ideální transformátor lze obecné závěry
(4.52)
,
(4.53)
a
(4.54)
vyjádřit v konkrétnějším tvaru, který ovšem
přibližně platí i pro reálné transformátory s těsnou vazbou k B
1.
Situaci budeme demonstrovat na jednoduchém příkladu transformátoru, jehož
primární a sekundární cívky mají postupně N1
a
N2 závitů a který je zapojen do obvodu podle obr. 4.16b.
(Předpokládáme přitom, že odpory R
1
a R2 reprezentují celkové odpory
primárního a sekundárního obvodu.) Za diskutovaných podmínek ideální těsné
vazby platí zřejmě
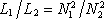 (srov. příklad 4.1.5e a úlohu Ú 4.9), odkud s
ohledem na relaci
(srov. příklad 4.1.5e a úlohu Ú 4.9), odkud s
ohledem na relaci
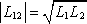 máme vztahy
máme vztahy
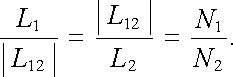 |
(4.57) |
Jejich dosazením do (4.52) a (4.53) dostáváme známé výsledky
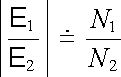 , , |
(4.58) |
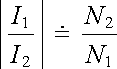 . . |
(4.59) |
Výraz (4.58) říká, že v transformátoru s rozpojeným sekundárem (transformátor naprázdno) se velikosti elektromotorického napětí transformují v poměru počtu závitů primáru k sekundáru. Proudy se naopak v transformátoru se zanedbatelným odporem sekundáru (transformátor nakrátko) podle (4.59) transformují v opačném poměru. Po dosazení (4.57) do (4.54) dostaneme dále
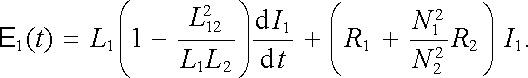 |
(4.60) |
Sekundární odpor R2 se tedy do primárního
obvodu transformuje v poměru čtverce počtu závitů. Z rovnic
(4.60)
rovněž
plyne, že efektivní indukčnost ideálního transformátoru je nulová.
Transformátor se tedy vůči zdroji E
1(t)
chová jako obvod s
čistě ohmickým odporem hodnoty
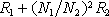 .
.
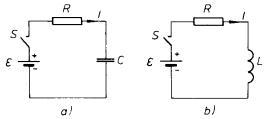
Vyšetřme poměry v obvodech s kapacitou a indukčností, v nichž působí časově neproměnné zdroje elektromotorického napětí (viz obr. 4.18). Odpor R představuje celkový odpor působící v obvodech, včetně vnitřního odporu zdroje. Budeme předpokládat, že spínač S je sepnut v čase t = 0, takže počínaje tímto okamžikem začne v obvodu působit zdroj časově neproměnného elektro-motorického napětí.
V případě obvodu s odporem a kapacitou (obr. 4.18a) dostaneme položením L = 0 v (4.39) pro proud I(t) rovnici


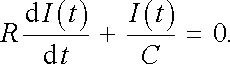 |
(4.61) |
Její obecný integrál má tvar
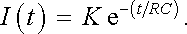 |
(4.62) |
Hodnotu integrační konstanty K určíme z počátečních podmínek. Při zapnutí obvodu má kondenzátor nulový náboj, takže podle (4.39) musí platit I(0)R = E . Dosazením do (4.62) dostaneme hledané partikulární řešení
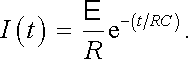 |
(4.63) |
Proud tekoucí obvodem nabíjí kondenzátor C. Pro okamžitou hodnotu napětí UC na kondenzátoru dostaneme z (4.37) podmínku I(t)R + UC = E , z níž po dosazení proudu podle (4.63) vyplyne
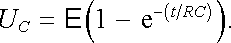 |
(4.64) |
Po
uplynutí dostatečně dlouhé doby je kondenzátor nabit na napětí UC,ℜ nekonecno
= E
a obvodem již dále neteče proud. Vypnutí spínače pak již nemá
vliv na poměry v obvodu; kondenzátor zůstane trvale nabit. V jeho dielektriku
zůstane elektrostatické pole o energii
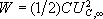 ,
která byla dodána zdrojem elektromotorického napětí.
,
která byla dodána zdrojem elektromotorického napětí.
Pro obvod znázorněný na obr. 4.18b platí rovnice (4.35) . Jde o nehomogenní lineární diferenciální rovnici prvního řádu. Její obecné řešení je dáno součtem libovolného partikulárního řešení a obecného řešení příslušné homogenní rovnice. Jelikož proud Iℜ nekonecno = E /R je triviálním řešením (4.35) , lze obecné řešení psát ve tvaru
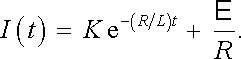 |
(4.65) |
Bezprostředně po zapnutí spínače bude mít proud obvodem nepatrnou hodnotu, neboť bude platit L(dI/dt) B E . Hodnotu integrační konstanty lze tedy určit užitím počátečních podmínek I(0) = 0 pro t = 0. Dostaneme pak hledané partikulární řešení
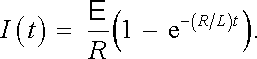 |
(4.66) |
Je z něj vidět, že proud v obvodu exponenciálně narůstá a asymptoticky se blíží k ustálené hodnotě Iℜ nekonecno = E /R. Na tuto ustálenou hodnotu proudu nemá již indukčnost L žádný vliv.
Při vypnutí spínače nastanou v obvodu složité poměry, neboť v indukčnosti L zaniká magnetické pole a jeho energie se musí nějakým způsobem zužitkovat. Nejčastěji nastává taková situace, že změnami proudu se v indukčnosti L indukuje elektromotorické napětí dostačující k tomu, aby mezi kontakty spínače zapálil jiskrový výboj. Tento výboj způsobí, že obvodem může téci proud ještě určitou dobu po vypnutí spínače a energie magnetického pole se částečně vyzáří a částečně přemění v Jouleovo teplo.
Obr. 4.19
Časová závislost napětí
a proudu v obvodech uvedených na obr. 4.18:
a) průběh proudu v obvodu s odporem a kapacitou, b) průběh napětí
na kondenzátoru,
c) průběh proudu v obvodu s indukčnosti.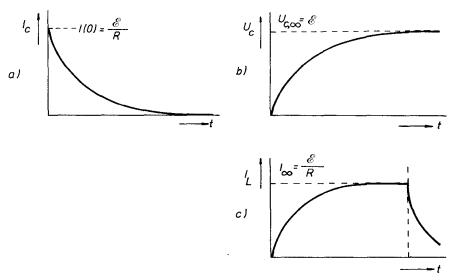
Odpor výbojové dráhy můžeme schematicky popsat zařazením odporu Rℜ' >> R paralelně ke kontaktům spínače. Proud obvodem po vypnutí spínače bude potom rovněž popsán obecným řešením (4.65) , v němž však je odpor R nahrazen odporem R'. Po dosazení počátečních podmínek I = E /R pro t = 0 a po zanedbání členu E /Rℜ' dostaneme pro průběh proudu
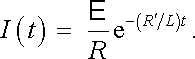 |
(4.67) |
Vidíme tedy, že proud po vypnutí spínače exponenciálně klesá. Na obrázku 4.19 jsou pro ilustraci uvedeny grafické závislosti vypočítaných veličin. Obrázek 4.19a zobrazuje proud obvodem s kapacitou, obr. 4.19b znázorňuje průběh napětí UC na kondenzátoru a konečně na obr. 4.19c vidíme průběh proudu v obvodu s indukčností.
Vyšetřme vlastnosti sériového spojení odporu R, indukčnosti L a kapacity C, které je připojeno k ideálnímu zdroji střídavého elektromotorického napětí frekvence ω , jehož okamžitá hodnota je dána vztahem (4.41) , ve kterém jsme pro zjednodušení položili φ = 0. (viz obr. 4.20).

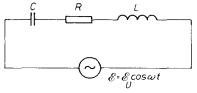
Aplikací II. Kirchhoffova pravidla dostaneme pro vyšetřovaný obvod rovnici, kterou lze převést na lineární diferenciální rovnici druhého řádu typu (4.39) , v níž je neznámou veličinou proud tekoucí obvodem
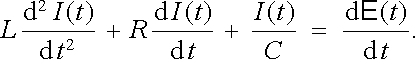 |
(4.68) |
Obecné řešení této rovnice lze, jak víme, vyjádřit jako sumu partikulárního řešení celé rovnice (4.68) a obecného řešení příslušné homogenní rovnice, tj. rovnice typu (4.43) , které má obecný tvar, viz (4.44) ,
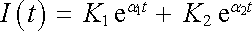 . . |
Konkrétní poměry v obvodu závisí jednak na charakteru kořenů α1, α2 charakteristické kvadratické rovnice a jednak na hodnotách integračních konstant K1, K2, jež jsou dány počátečními podmínkami. Příspěvek obecného integrálu (4.44) homogenní rovnice k celkovému proudu v obvodu závisí tedy mimo jiné na tom, ve kterém bodě periody elektromotorického napětí je zdroj k obvodu připojen.
Z diskuse vlastností řešení (4.44) provedené v článku 4.2.2 však plyne, že bez ohledu na konkrétní hodnoty parametrů obvodu či na hodnoty počátečních podmínek se jeho hodnota asymptoticky blíží k nule pro t ℜ → ℜ nekonecno . Po dostatečně dlouhé době od zapnutí zdroje můžeme příspěvek obecného integrálu homogenní rovnice k celkovému proudu zanedbat. Obecný integrál homogenní rovnice ovlivňuje tedy proud jen v neustáleném stavu a nebudeme se jím dále zabývat.
Ustálený stav obvodu je tudíž určen jen partikulárním řešením celé nehomogenní rovnice (4.68) . Je přirozené předpokládat, že po dostatečně dlouhé době od zapnutí zdroje bude charakter časové závislosti proudu v obvodu určen jen charakterem časové závislosti elektromotorického napětí. Partikulární řešení rovnice (4.68) budeme tedy hledat ve tvaru
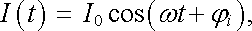 |
(4.69) |
přičemž hodnoty parametrů I0 a φ i , určíme z požadavku, aby toto řešení rovnici (4.68) vyhovovalo. Po provedení příslušných derivací a dosazení do (4.68) dostaneme podmínku
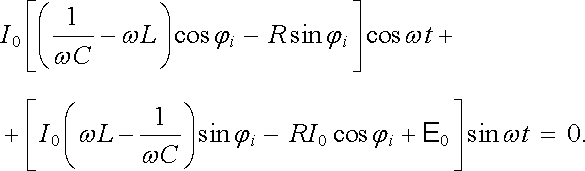 |
(4.70) |
Má-li být tato podmínka splněna v libovolném okamžiku, musí být koeficienty u cos ω t a sin ω t rovny nule. Tedy
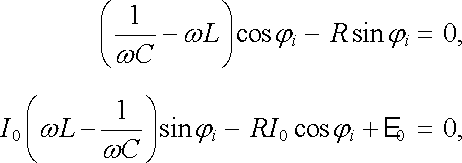 |
(4.71) |
což jsou rovnice pro hledané parametry φ i a I0. Z první rovnice (4.71) dostaneme pro φ i
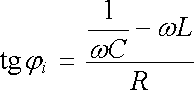 |
(4.72) |
a pro I0 platí
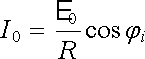 |
(4.73) |
nebo (s využitím identity
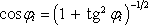 ) také
) také
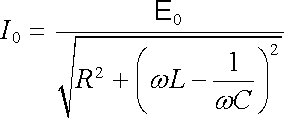 . . |
(4.74) |
Srovnáním s definičním vztahem (4.50) dostáváme pro impedanci sériového spojení odporu, indukčnosti a kapacity
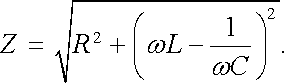 |
(4.75) |
Z výsledku (4.75) vidíme, že impedance, a tedy i amplituda proudu je nemo-notónní funkcí frekvence ω . Impedance má minimální hodnotu Zmin = R, platí-li ω L = 1/ω C, tj. je-li frekvence zdroje ω rovna frekvenci ω 0 podle vztahu (4.47) . Při této frekvenci má amplituda proudu maximální možnou hodnotu
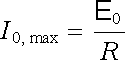 . . |
(4.76) |
Právě vyšetřovaný obvod (viz obr. 4.20) se nazývá sériovým rezonančním obvodem. Závislost amplitudy proudu na frekvenci zdroje se nazývá rezonanční křivkou obvodu. V případě, že pro frekvenci zdroje platí (4.47)
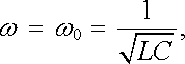 |
říkáme, že obvod je v rezonanci.
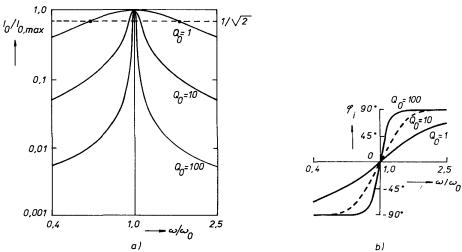
Obr. 4.21 Rezonanční křivky sériového rezonančního obvodu: a) redukovaná frekvenční závislost amplitudy napětí a proudu, b) redukovaná frekvenční závislost fázového úhlu.
Na obrázku 4.21 jsou uvedeny příklady tzv. redukované rezonanční křivky, která
představuje závislost I0
/I0
,max na ω
/
ω
0. Důležitým pojmem je tzv. pološířka rezonanční křivky Δ
ω
definovaná jako absolutní hodnota rozdílu frekvencí ω
1 a ω
2,
při nichž má proud hodnotu
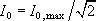 (viz obr. 4.21a). Pro frekvence ω
1
a ω
2
zřejmě platí
(viz obr. 4.21a). Pro frekvence ω
1
a ω
2
zřejmě platí
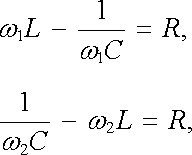 |
(4.77) |
takže
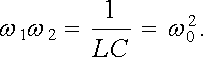 |
(4.78) |
Sečtením obou vztahů (4.77) dostaneme dále pro šířku rezonanční křivky výsledek
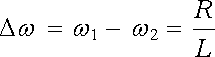 . . |
(4.79) |
V relativní míře pak platí
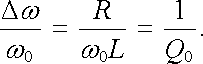 |
(4.80) |
Veličina Q0 charakterizující relativní šířku rezonanční křivky se nazývá (vlastním) činitelem jakosti obvodu.
Pro obvod v rezonanci platí podle (4.72) φ i = 0. Se vzdalováním od rezonance se konstanta φ i, charakterizující fázový posuv proudu vůči elektromotorickému napětí zdroje, blíží hodnotám ℜ ± π /2. Obrázek 4.21b demonstruje tuto závislost pro obvody o různém činiteli jakosti.
Uvažme dvojici obvodů s indukčností, odporem a kapacitou, vázané vzájemnou indukčností L12 (viz obr. 4.22). Pro vyšetření charakteru vlastních kmitů těchto obvodů musíme řešit soustavu lineárních diferenciálních rovnic
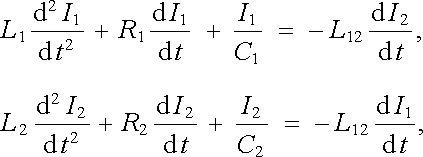 |
(4.81) |
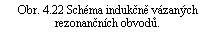
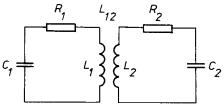
kterou dostaneme použitím II. Kirchhoffova pravidla. Pro jednoduchost se omezíme na dvojici identických obvodů s nulovým tlumením, tj. položíme L1 = L2 = L, C1 = C2 = C, R1 = R2 = 0. Místo (4.81) proto máme
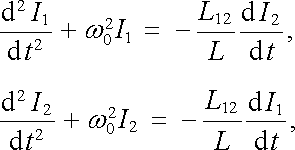 |
(4.82) |
kde
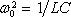 .
Zavedeme-li veličiny I (+) = I1 + I2,
I (-) = I1 - I2,
dostaneme sečtením a odečtením posledních rovnic
.
Zavedeme-li veličiny I (+) = I1 + I2,
I (-) = I1 - I2,
dostaneme sečtením a odečtením posledních rovnic
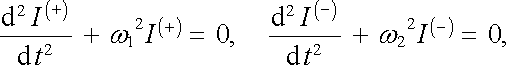 |
(4.83) |
v nichž jsme označili (srov. čl. 4.2.3)
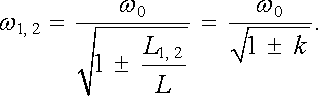 |
(4.84) |
Obecným řešením těchto rovnic je zřejmě
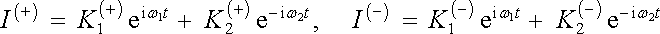 . . |
(4.85) |
V obvodech existují tedy současně kmity o dvou frekvencích ω 1 a ω 2 daných vztahem (4.84) .
Vázané oscilační obvody tvoří elektrickou analogii vázaných mechanických oscilátorů, neboť obě soustavy jsou popsány rovnicemi stejného typu. V elektrotechnice se obou prvků, i jejich vzájemné kombinace, hojně využívá především ke konstrukci frekvenčních filtrů.