---

---

4.3 Energie kvazistacionárního pole

4.3.1 Zákon zachování energie v kvazistacionárních soustavách

Dříve než přistoupíme k vlastnímu výkladu dané problematiky, krátce zrekapi­tulujeme, co bylo o energii vyloženo v předchozích kapitolách. V kapitole l byla věnována značná pozornost energii jednotlivých typů elektrostatických soustav (viz čl. 1.1.5, 1.2.8, 1.4.6 a 1.5.5). Nejdůležitější diskutovanou problematikou byly různé formy vyjádření energie elektrostatického pole, přičemž jsme tímto pojmem rozuměli záporně vzatou práci, kterou musely vykonat vnější síly při vytváření konečné konfigurace dané elektrostatické soustavy. Důležitý byl rov­něž předpoklad, že veškerá uvedená práce byla vynaložena na překonání elektro­statických sil mezi náboji. Tyto síly pak mohou při pohybu nábojů samy konat práci na vrub energie elektrostatického pole; v elektrostatickém stavu, kdy jsou všechny náboje v klidu, je však energie elektrostatického pole konstanta a elektrostatické pole žádnou práci nekoná.

V oddílu 3.2 byly uvedené pojmy zobecněny pro případ stacionárního elektrického pole. Díky tomu, že stacionární elektrické pole je popsáno formálně totožnými rovnicemi jako pole elektrostatické, je energie stacionárního elektrického pole rovněž konstantní a může být vyšetřována analogickým způsobem (viz článek 3.2.5). Kvalitativně novou skutečností je však platnost Jouleova zákona, který vyjadřuje zákon zachování energie pro stacionární pole ve vodiči. Stacionární elektrické pole ve vodiči může být trvale udržováno jen působením pole vtištěných sil, které trvale konají práci, jež se spojitě mění v Jouleovo teplo. V následujících oddílech kapitoly 3, ve kterých byly probírány vlastnosti stacionárního magnetického pole, nebylo nic řečeno o jeho energii. Důvodem tohoto rozdílného postupu je skutečnost, že ve stacionárním přiblížení není možné vzít v úvahu jev elektromagnetické indukce, jehož započtení umožňuje nový, obecnější pohled na řešenou problematiku. Výklad vlastností energie kvazistacionárního pole bude naším úkolem tohoto oddílu. Zákonitosti platné pro energii stacionárního magnetického pole vyplynou ze získaných výsledků jako speciální případ pro časově nezávislé magnetické pole.

Energetickou bilanci kvazistacionární soustavy vyšetříme nejdříve na pří­kladu obvodu (smyčky) sestávajícího ze sériového spojení indukčnosti L, kapa­city C a odporu R_c, ve kterém působí zdroj časově proměnného elektromotoric­kého napětí E (t) (viz obr. 4.11). Budeme sledovat děje v tomto obvodu, které nastanou ve velmi krátkém časovém intervalu dt, ve kterém proud I (t) tekoucí obvodem přenese libovolným průřezem vodiče náboj dQ = I(t)dt . Vynásobe­ním rovnice (4.38) tímto nábojem dostaneme

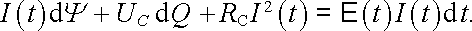(4.86)

Platnost získaného výsledku jako celku je nepochybná, neboť rovnice (4.86) je důsledkem obecných zákonitostí platných pro kvazistacionární soustavu. Otáz­kou však zůstává fyzikální interpretace jednotlivých členů, která může být ur­čena jen na základě experimentu. Tato interpretace musí být ovšem konzistentní s dříve vyloženými zákonitostmi pro elektrostatické a elektrické stacionární pole, jež můžeme chápat jako speciální případy pole kvazistacionárního.

Člen E (t)I(t)dt na pravé straně je totožný s výrazem udávajícím práci doda­nou do stacionárního obvodu vtištěnými silami v časovém intervalu dt (srov. čl. 3.2.5). Experiment dále ukazuje, že platnost vztahů pro práci vtištěných sil, uve­dených v citovaném článku, zůstává zachována i pro kvazistacionární soustavu; výraz

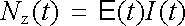(4.87)

tedy představuje okamžitý výkon dodávaný zdrojem elektromotorického napětí (vtištěnými silami) do kvazistacionárního obvodu. Podobná shoda je i u posled­ního členu na levé straně; výraz R_CI²(t) podle (3.45) vyjadřuje okamžitý výkon přeměňovaný ve vodičích obvodu na Jouleovo teplo.

Další shodu s dříve vyloženými zákonitostmi představuje i druhý člen U_CdQ na levé straně, který je podle článku 1.4.6 totožný s výrazem reprezentujícím změnu energie elektrostatického pole kondenzátoru, spojenou se změnou jeho náboje dQ. Tato shoda ovšem nepřekvapuje, neboť elektrostatické, elektrické stacionární i kvazistacionární pole je popsáno formálně shodnými rovnicemi. Veškerá dosavadní experimentální zkušenost dále potvrzuje, že (podobně jako v případě stacionárního elektrického pole) i pro vyjádření energie kvazistacio­nárního pole mohou být použity všechny postupy vyložené v článcích 1.2.8, 1.4.6 a 1.5.5.

Konečně zbývající první člen na levé straně (4.86) nemá v dosavadním vý­kladu obdobu. Je přirozené předpokládat, že reprezentuje energii dW_m potřeb­nou ke změně magnetického toku dΨ . Tedy

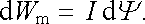(4.88)

Experiment tento předpoklad plně potvrzuje. V následujícím článku budou po­drobněji studovány procesy související s touto energií.

Dosud vyložená fakta umožňují formulovat konkrétní tvar zákona zachování energie pro kvazistacionární elektromagnetickou soustavu:

Energie dodávaná polem vtištěných sil se mění jednak na Jouleovo teplo, jednak je vynakládána na změny elektrického a magnetického pole.

Právě formulovaná věta o energii kvazistacionární soustavy a vzorec (4.88) mohou být využity pro vyjádření energie magnetického pole. V obecné formě je však tato problematika dosti složitá, neboť integrace vztahu (4.88) je možná jen při znalosti vlastností prostředí, v němž se pole nachází. Jednoduchá je situace pro lineární prostředí, kdy lze využít vztah (4.14) . Po integraci diferenciálu (4.88) lze získat vzorec pro energii W_m magnetického pole buzeného smyčkou (zhotovenou z vodiče o malém průřezu) o vlastní indukčnosti L, jíž protéká proud I vytvářející celkový magnetický tok Ψ , viz (4.91) ,

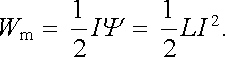Postup integrace i získaný výsledek je analogií vzorce (1.208) pro elektrostatic­kou energii nabitého vodiče. Podobnou analogií (a to opět v postupu i výsledku) je možnost vyjádřit energii magnetického pole v lineárním prostředí objemovým integrálem typu (1.266) z objemové hustoty energie, viz (4.100) ,

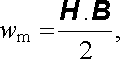která má i v kvazistacionární soustavě jen formální význam.

V následujícím článku je výraz (4.88) zobecněn pro libovolný počet smyček a problematika vyjádření energie magnetického pole (včetně odvození vztahů (4.91) a (4.100) ) je diskutována v relativně obecné formě.

4.3.2 Obecné vyjádření energie magnetického pole

Postup použitý v předchozím článku lze jednoduše zobecnit. Uvažujme soustavu N smyček tvořených vodiči zanedbatelného průřezu protékaných proudy I₁, I₂, ..., I_N. Energie δ W_m potřebná ke změně celkových magnetických toků δ Ψ ₁, δ Ψ ₂,..., δ Ψ _N jednotlivými smyčkami je podle předchozího článku zřejmě dána vztahem

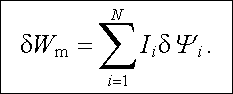(4.89)

Získaný výsledek představuje základní vztah pro výpočet energie magnetic­kého pole. Je však třeba si na tomto místě uvědomit, že veškerá energie δ W_m nemusí vždy reprezentovat energii vytvořeného magnetického pole, která může být soustavou navrácena při jeho zrušení. V závislosti na konkrétních vlastnos­tech daného hmotného prostředí může být část energie δ W_m spotřebována na nevratné procesy (především na přeměnu v teplo) spojené se změnou magneti­zace látek. Procesy tohoto druhu se uplatňují především v nelineárních magneti­kách jevících hysterezi (například ve feromagnetikách); konkrétní příklad tako­vého chování bude vyšetřen v 4.3.4b.

V případě, kdy je celý prostor vyplněn lineárním prostředím, může být vztah (4.89) jednoduše použit k vyjádření energie magnetického pole. Označíme-li vlastní indukčnosti jednotlivých smyček L₁, L₂, ..., L_N, L_ik vzájemnou indukč­nost mezi jejich libovolnou dvojicí a předpokládáme-li, že tyto indukčnosti ne­závisí na protékajících proudech smyčkami, můžeme vztah (4.89) jednoduše integrovat. Pro integraci lze použít stejný postup, který byl použit v článku 1.4.6 pro získání výrazu (1.209) . Integrujeme-li v mezích od nuly do konečných hod­not proudů I₁, I₂, ..., I_N, dostaneme pro energii magnetického pole

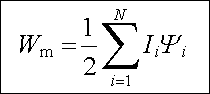(4.90a)

nebo, vyjádříme-li celkové magnetické toky jednotlivými smyčkami pomocí (4.16) ,

.

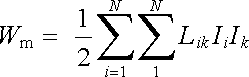(4.90b)

Speciálně pro jedinou smyčku platí

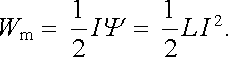(4.91)

Vztahy (4.90) představují analogii výrazu (1.209) pro energii elektro-statického pole soustavy vodičů. Podobně jako byla tato elektrostatická soustava (při dané geometrické konfiguraci) zadána potenciály a náboji jednotlivých vo­dičů, je naše magnetická soustava (při dané geometrii smyček) zadána jejich proudy a celkovými magnetickými toky. Hodnoty těchto toků mají však dobrý smysl jen tehdy, jsou-li všechny smyčky tvořeny vodiči zanedbatelného průřezu. Není-li tato podmínka splněna, nelze výrazy (4.88) až (4.91) použít a pro vyjád­ření energie je třeba volit jiný postup, který nyní naznačíme.

Magnetický tok Ψ _i i-tou smyčkou lze podle (4.20) vyjádřit pomocí vektoro­vého potenciálu

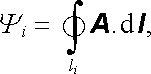(4.92)

přičemž naznačená integrace je brána přes celý obvod l_i smyčky. Podobně proud I_i můžeme vyjádřit pomocí proudové hustoty ve tvaru plošného integrálu typu (3.5)

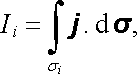(4.93)

přičemž naznačená integrace je uvažována přes libovolný průřez σ _i vodiče smyčky. Po dosazení do (4.89) můžeme energii δ W_m vyjádřit ve tvaru

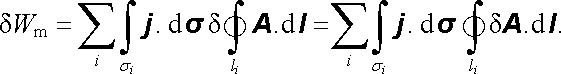Uvědomíme-li si, že platí dV = dσ  .dl , kde dV je element objemu vodiče, je zřejmé, že dvojí integraci v posledním výrazu, přes obvody a průřezy jednotli­vých vodičů, lze nahradit jediným objemovým integrálem přes celý objem vo­dičů V₀. Aniž bychom se zabývali matematickou stránkou této operace, která je podrobněji popsána například v [6], můžeme výsledek napsat ve tvaru

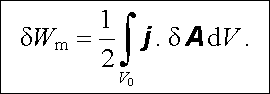(4.94)

Pro případ lineárního prostředí, kdy je vektorový potenciál A (r , t) úměrný proudu, lze jednoduše provést integraci (4.94) a vypočítat energii magnetického pole. Integrace v mezích od nuly do konečného rozdělení proudu dá pro tuto energii výsledek

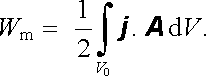(4.95)

Vztah (4.94) , popř. (4.95) , je alternativní k (4.89) , popř. (4.90) , pro vyjádření energie δ W_m , popř. W_m . Je zřejmé, že ve volbě oboru integrace v  (4.94) a (4.95) existuje značná libovůle. Vzhledem k tomu, že proudová hustota j je nulová mimo vodiče uvažovaných proudových smyček, může být obor integrace V₀ nahrazen libovolným objemem V obsahujícím celý objem vodičů, aniž se změní hodnoty integrálů.

Třetí obecnou možností je vyjádření energie magnetického pole pomocí vek­torů magnetické indukce a intenzity magnetického pole. Východiskem pro toto vyjádření může být vztah (4.94) , ve kterém proudovou hustotu j nahradíme rot  H podle Amp`erova zákona (3.138) . Integrovanou funkci δ A   .   rot  H je pak možné dále upravit využitím identit vektorové analýzy. Podle (D 1.55) platí

,

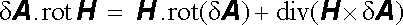odkud po záměně pořadí operací rotace a diferencování dostaneme

.

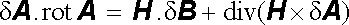Energie δ W_m může být tedy vyjádřena ve tvaru

,

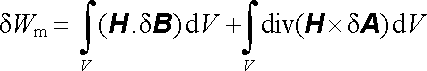(4.96)

přičemž ve smyslu uvedené poznámky může být obor integrace V zvolen libo­volně za předpokladu, že obsahuje objem V₀ všech vodivých smyček uvažované soustavy. Tato libovůle ve volbě oboru integrace není již ovšem tak průhledná jako v případě samotného vztahu (4.94) , neboť intenzita magnetického pole i magnetická indukce jsou obecně nenulové i v bodech s nulovou hustotou proudu. Z použitého postupu však vyplývá, že se změnou oboru integrace se změní jen podíl jednotlivých členů z pravé strany (4.96) na výsledné hodnotě δ W_m . Sama tato hodnota je však na volbě V nezávislá.

Uvedenou skutečnost je možné využít ke zjednodušení (4.96) , rozšíříme-li obor integrace na celý prostor. Použijeme-li totiž Gaussovu větu, můžeme druhý člen na pravé straně (4.96) převést na plošný integrál přes plochu S ohraničující objem V, který, jak víme, musí obsahovat všechny vodiče uvažované soustavy. Dostaneme tak

.

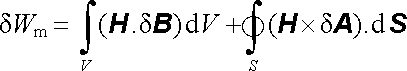(4.97)

Při rozšíření oboru integrace do nekonečna, V ℜ →  V_{ℜ nekonecno} , hodnota plošného integrálu klesne na nulu, neboť integrovaná funkce s r ℜ →  0 klesá jako r^-3, zatímco plocha S vzrůstá jen jako r². Celkem tedy platí

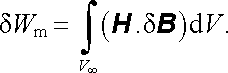(4.98)

Získaný výsledek představuje vedle (4.89) a (4.94) další možnost obecného vy­jádření přírůstku energie δ W_m souvisejícího s odpovídající změnou magnetic­kého pole. Jsou-li známy magnetické vlastnosti prostředí vyplňujícího prostor, je možné provést integraci (4.98) od počátečního nulového pole do jeho konečné hodnoty. Pro ideální (lineární) magneticky měkké prostředí popsané permeabi­litou dostaneme

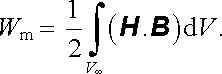(4.99)

Vztah (4.98) je analogický s výrazem (1.265) pro elektrostatické pole a podobně vztah (4.99) je analogický s (1.266) . Je tedy rovněž možné v analogii s (1.267) chápat veličinu

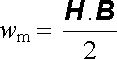(4.100)

jako objemovou hustotu energie magnetického pole. Avšak i v kvazistacionár­ním přiblížení platí o fyzikálním významu této veličiny totéž, co bylo o významu hustoty energie elektrostatického pole řečeno v kapitole l (srov. články 1.2.8, 1.4.6 a 1.5.5). Fyzikální význam má jen celková energie W_m a je lhostejné, kterým z výrazů (4.90) , (4.95) , (4.99) je vyjádřena.

Nakonec si ještě stručně všimneme potenciální energie magnetického tělesa ve vnějším magnetickém poli B ₀. Jelikož lze tento problém řešit v podstatě stej­ným způsobem jako problém potenciální energie dielektrického tělesa v elek­trickém poli (srov. čl. 1.5.5), uvedeme jen výsledky. (Podrobněji je tato proble­matika rozvedena například v [7].) Přírůstek hledané potenciální energie δ W je dán objemovým integrálem

,

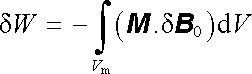(4.101)

přes objem V_m magnetického tělesa, v němž M je jeho magnetizace. Hustotu přírůstku této energie δ w lze pak vyjádřit vztahem

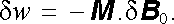(4.102)

Celkovou potenciální energii lze počítat jen v případě, známe-li vzájemnou sou­vislost M a B ₀. Situace je jednoduchá v případě ideálně tvrdého a ideálně měk­kého (lineárního) prostředí.

V případě ideálně tvrdého magnetika o magnetizaci M ₀ dostáváme (srov. vztah (1.271) a rovněž (3.107) )

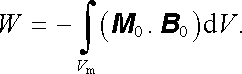(4.103)

V případě ideálně měkkého prostředí dostáváme analogicky s (1.273)

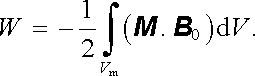(4.104)

Na rozdíl od dielektrika však veličina (M . B ₀) může být kladná i záporná; zá­porných hodnot nabývá pro diamagnetická tělesa.

4.3.3 Obecné vyjádření sil v magnetickém poli

Pro obecné vyjádření sil působících na vodič v magnetickém poli lze vyjít přímo z definičního vztahu pro magnetickou indukci (srov. čl. 3.3.1). Pro sílu f půso­bící na jednotkový objem vodiče s proudovou hustotou j platí (3.58)

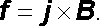Síla F působící na celý vodič, ve kterém se uzavírá daný proud, je pak dána inte­grálem přes jeho celý objem V. Tedy

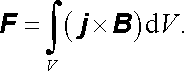(4.105)

Magnetická indukce B v (3.58) představuje celkovou magnetickou indukci v daném bodě, která může být obecně buzena jak vnějšími zdroji, tak i jinými částmi vlastního vyšetřovaného vodiče. Je však zřejmé, že vlastní magnetické pole buzené tímto vodičem nemůže mít žádný dynamický účinek na vodič jako celek (pokud jej považujeme za tuhou soustavu). Při integraci naznačené ve vztahu (4.105) je proto možné se omezit jen na pole buzené vnějšími zdroji.

Pro vodiče ve tvaru tenkých proudových smyček je možné výraz (4.105) vyjádřit i v jiném tvaru. Uvážíme-li korespondenci j dV  ℜ ↔  Id l (srov. čl. 3.3.3), můžeme místo (4.105) napsat

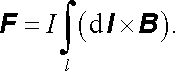(4.106)

Alternativně je možné vyjádřit síly působící na smyčku protékanou proudem i pomocí energie magnetického pole soustavy (srov. analogickou situaci v elektrostatickém poli - čl. 1.4.6). Uvažujme soustavu N tuhých nedeformovatelných smyček protékaných proudy I₁, I₂,..., I_N, v nichž působí vnější zdroje elektromotorických napětí E ₁, E ₂,..., E _N. Vzorce (4.90) ukazují, že v lineárním prostředí je energie magnetického pole soustavy W_m jednoznačnou funkcí vzájemné konfigurace smyček. Označíme-li tedy { &ksi; _i} soubor zobecněných souřadnic plně popisujících jejich prostorové rozmístění, můžeme za uvedeného předpokladu napsat

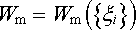(4.107)

a energetickou bilanci soustavy při změně souřadnic využít k výpočtu sil působících na jednotlivé smyčky.

Předpokládejme, že jedna ze smyček změní svou polohu tak, že se její souřadnice &ksi; _i změní o hodnotu Δ &ksi; _i , přičemž zbylé souřadnice zůstanou konstantní. Soustava zřejmě vykoná mechanickou práci A, již lze vyjádřit vztahem

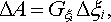v němž 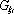představuje složku zobecněné síly příslušné souřadnici &ksi; _i . Při změně polohy smyčky se obecně změní také hodnoty magnetických toků tekoucích jednotlivými smyčkami o určité hodnoty Δ Ψ ₁,..., Δ Ψ _N a pohyb smyčky vyvolá vznik indukovaného elektromotorického napětí ve všech smyčkách. Budeme-li předpokládat, že se posunutí smyčky uskuteční v časovém intervalu Δ t , bude možné podle (4.86) vyjádřit energetickou bilanci každé smyčky vztahem

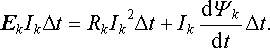Pro celou soustavu tedy dostaneme

.

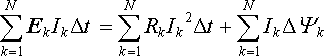(4.108)

Označme Δ W tu část energie dodané vnějšími zdroji elektromotorického napětí, která se nespotřebuje na Jouleovo teplo

.

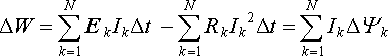(4.109)

S ohledem na zákon zachování energie v kvazistacionární soustavě (srov. čl. 4.3.1) je nutné soudit, že tato energie se spotřebuje jednak na změnu energie magnetického pole Δ W_m , jednak na vykonání mechanické práce Δ A . Musí tedy platit podmínka

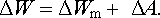(4.110)

V praxi jsou důležité dva speciální případy. Za prvé budeme předpokládat, že při posunutí smyčky zůstanou zachovány toky jednotlivými smyčkami (tj. že Δ Ψ _k  = 0 pro k = 1,..., N). Potom z  (4.109) plyne a podle (4.110) platí

.

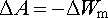(4.111)

Pro sílu 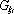tedy dostáváme

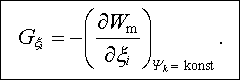(4.112)

Za druhé nechť při posunování smyčky zůstanou konstantní proudy I₁, I₂,..., I_N. Pro změnu energie magnetického pole soustavy pak z (4.90) plyne

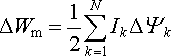a podle (4.109) platí Δ W  = 2Δ W_m . Po dosazení do podmínky (4.110) tedy dostaneme

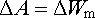(4.113)

a sílu 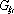můžeme vyjádřit ve tvaru

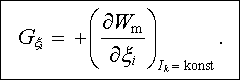(4.114)

Právě vyložený postup založený na bilanci energie byl v elementárnější formě použit v článku 3.4.2 při odvozování vztahů (3.108)

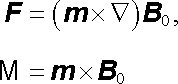pro sílu F a moment síly M působící na magnetický dipól s magnetickým momentem m ve vnějším magnetickém poli B ₀. Je zřejmé, že tyto vzorce budou přibližně použitelné i pro vyjádření sil působících na útvary konečných rozměrů s pevným, na vnějším magnetickém poli nezávislým magnetickým momentem m (tj. například na magneticky tvrdá zmagnetovaná tělesa či na proudové smyčky), pokud vnější magnetické pole nebude příliš nehomogenní.

4.3.4 Řešené příklady

a) Síly působící mezi póly elektromagnetu

Uvažujme elektromagnet podle obr. 4.23, tvořený magnetickým obvodem z feromagnetického materiálu o vysoké relativní permeabilitě _r, se vzduchovou mezerou délky l. Nechť proud I tekoucí cívkou vybudí v mezeře magnetické pole B ₀, které lze v prvním přiblížení považovat za homogenní.

Mezi póly magnetu bude působit síla F , která může být snadno vypočtena užitím vztahu (4.112) . Energie magnetického pole elektromagnetu může být vypočtena pomocí vztahu (4.99) , přičemž integrovat je obecně třeba přes celý objem mezery i jádra. V případě _r >>  1 je hustota energie magnetického pole v jádru w_m = H .B /2 =  mnohem nižší než ve vzduchové mezeře. Proto i když je objem jádra obecně větší než objem pole ve vzduchové mezeře, lze celkovou energii magnetického pole elektromagnetu v prvním přiblížení repre­zentovat jen energií pole v mezeře. Označíme-li plochu pólů magnetu S a budeme-li pole v mezeře považovat za homogenní, dostaneme pro tuto energii přibližný výraz

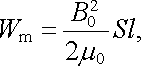(4.115)

podle něhož je energie lineární funkcí délky mezery l. V uvedeném přiblížení předpokládáme, že hustota energie w_m, a tedy i magnetická indukce B ₀, jsou nezávislé na délce mezery. Pro výpočet síly F lze tedy použít vztah (4.112) , čímž získáme výsledek

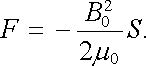(4.116)

Póly magnetu se tedy uvedenou silou přitahují.

b) Hysterezní ztráty ve feromagnetiku

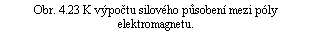
Již v úvodu článku 4.3.2, v komentáři ke vztahu (4.89) bylo zdůrazněno, že veš­kerá energie W_m spojená se změnou magnetického pole nemusí být rovna změně energie magnetického pole, která může být navrácena při jeho zániku. Situace závisí na konkrétních vlastnostech prostředí vyplňujícího prostor, v němž je magnetické pole vytvořeno. Typickým příkladem je chování feromagnetika, které nyní vyšetříme.

Vztah mezi magnetizací (respektive magnetickou indukcí) a intenzitou pole ve feromagnetiku je nejednoznačný a obvykle je popisován soustavou hysterez­ních smyček (srov. čl. 3.5.4). Předpokládejme například, že chceme vypočítat energii připadající na jednotkový objem feromagnetika, která je potřebná k jeho přemagnetování po klesající větvi hysterezní smyčky z bodu (B) do bodu (D) (viz obr. 3.33). Pro tento výpočet lze vyjít ze vztahu (4.98) , provedeme-li inte-graci energie δ w_m připadající na jednotkový objem v mezích od B_(B) do B_(D). Po integraci metodou per partes dostaneme

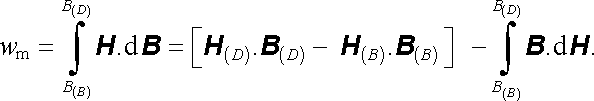(4.117)

Při cyklickém přemagnetování (například opět z výchozího bodu B_(B), kdy pra­covní bod proběhne postupně celou hysterezní smyčkou, bude výchozí a ko­nečné pole totožné. První člen v (4.117) bude tedy nulový a pro energii w_m do­staneme

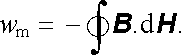(4.118)

Při průběhu jednoho cyklu hysterezní smyčky se energie magnetického pole nezmění. Celá energie w_m podle (4.118) se tedy spotřebovává na přemagneto­vání feromagnetika a je nevratně přeměněna v teplo. Obvykle se tato energie nazývá hysterezními ztrátami daného feromagnetika. Z geometrického významu integrálu (4.118) vyplývá, že hysterezní ztráty jsou dány plochou hysterezní smyčky.

c) Střední hodnota výkonu ve střídavém obvodu

V článku 4.3.1 bylo ukázáno, že okamžitá hodnota výkonu dodávaného zdroji elektromotorického napětí do kvazistacionárního obvodu je dána vztahem (4.87) . Tato veličina je ovšem obecně časově závislá a není vhodná pro prak­tické použití. Jednoduchá situace nastává v ustáleném stavu střídavého obvodu, kdy je možné dodávaný výkon charakterizovat časově nezávislou střední hod­notou, kterou nyní vypočteme.

Předpokládejme, že zdroj dodává do obvodu elektromotorické napětí, jehož časový průběh je dán vztahem (4.41) . V ustáleném stavu může být okamžitá hodnota proudu I(t) dodávaného do obvodu vyjádřena vztahem (4.48) . Střední hodnotu výkonu za dobu jedné periody T = 2π /ω můžeme získat jednoduchým výpočtem. Platí

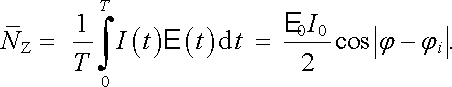(4.119)

Jak je vidět, dodávaný výkon závisí nejen na amplitudách elektromotorického napětí E ₀ a proudu I ₀ , ale také na jejich vzájemném fázovém posuvu | φ  -  φ _i | . Veličina cos| φ  - φ _i | se nazývá účiník.

Často se pro vyjadřování střídavých napětí a proudů zavádí pojem efektivních hodnot 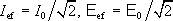. Jejich užitím lze výkon vyjádřit vztahem

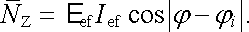(4.120)

Je zřejmé, že vztahy typu (4.119) , popř. (4.120) , lze vyjádřit nejen výkon 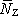dodávaný zdrojem do obvodu, ale také výkon ztracený na jednotlivých prvcích obvodu. Podobně lze výpočet střední hodnoty výkonu pomocí integrálu typu (4.119) , i zavedení efektivní hodnoty napětí a proudu zobecnit pro případ nesi­nusových periodických průběhů (srov. čl. 8.3.1).

d) Magnetoelektrický měřicí přístroj

Silových účinků magnetického pole na vodiče protékané proudem využívá vět­šina analogových přístrojů pro měření napětí a proudu. Nejužívanější z nich je tzv. magnetoelektrický systém (nazývaný též systém Deprezův-ďArsonvalův), jehož princip je uveden na obr. 4.24. Pólové nástavce trvalého magnetu jsou vytvarovány tak, aby mezi nimi vznikla válcová dutina, v níž je vloženo rovněž válcové jádro z feromagnetického materiálu. Podle výsledků příkladu 3.5.7a vznikne v mezeře mezi pólovými nástavci a jádrem radiální magnetické pole B . V této mezeře je dále umístěna obdélníková cívka, která je otočná kolem osy totožné s osou jádra. Cívka je zavěšena buď na torzním vlákně, nebo je uložena v hrotových ložiskách doplněných spirálovými pružinami sloužícími jako pří­vody. Závěs torzního vlákna, respektive spirálové pružiny slouží zároveň k vy­mezení rovnovážné klidové polohy cívky. Při jejím vychýlení z této klidové polohy vzniká vlivem elastické deformace vlákna či pružiny tzv. direkční mo­ment, který se snaží navrátit cívku do klidové polohy. Výchylka cívky z klidové polohy, charakterizovaná úhlem α , tvoří měřicí údaj přístroje. Je indikována buď mechanicky (ručkou), nebo opticky, pomocí zrcátka.

Obr. 4.24 Princip uspořádání magnetoelektrického měřicího přístroje.

Mechanické vlastnosti systému jsou charakterizovány jednak momentem setrvačnosti J _s cívky, jednak silovými momenty na ní působícími: momentem magnetických sil buzených proudem protékajícím cívkou D _m, direkčním mo­mentem D _d a brzdicím momentem D _b.

Podstatnou vlastností dané konstrukce přístroje je, že moment magnetických sil působících na cívku je nezávislý na její poloze, tj. na úhlu α jejího vytočení z rovnovážné polohy. Na cívku o N závitech, výšce l a šířce b, jejíž plocha S je tedy rovna S = lb, působí podle čl. 3.4.2 (při dané geometrii magnetického pole) moment

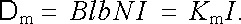(4.121)

Direkční moment D _d může být vyjádřen vztahem

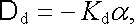(4.122)

v němž K_d je konstanta určená vlastnostmi závěsného systému. Brzdicí moment je dán jednak odporem vzduchu při pohybu cívky, zejména je však dán induko­vanými proudy vznikajícími při pohybu vodivých součástí cívky v magnetickém poli. Snadno se přesvědčíme, že výsledný brzdicí moment bude úměrný úhlové rychlosti cívky. Tedy

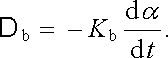(4.123)

Užitím 2. impulsové věty dostaneme pohybovou rovnici cívky

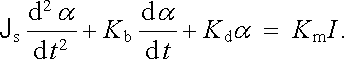(4.124)

Jde vlastně o rovnici torzního kyvadla, charakter jejíhož řešení závisí na hodno­tách kořenů charakteristické rovnice. Matematická stránka řešení (4.124) je po­dobná jako řešení rovnice (4.43) pro vlastní kmity obvodu RCL. V zásadě exis­tují dva typy řešení: periodické a aperiodické. Získá-li cívka systému v nulovém okamžiku určitou hybnost, která ji vychýlí z klidové polohy, pak v aperiodickém stavu se vrací do klidové polohy způsobem kvalitativně zobrazeným na obr. 4.14. V periodickém stavu naopak koná tlumené kmity kolem rovnovážné po­lohy, jejichž perioda T₀ je dána známým vztahem (srov. obr. 4.15)

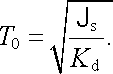(4.125)

Důležitý je tzv. kritický aperiodický stav, který představuje rozhraní mezi perio­dickým a aperiodickým stavem a odpovídá dvojnému kořenu charakteristické rovnice. V tomto stavu zaujímá systém rovnovážnou klidovou polohu nejrych­lejším možným způsobem.

Magnetoelektrický měřicí přístroj umožňuje několik typů použití: především jako měřidlo časově neproměnného proudu, dále jako měřidlo náboje (proudo­vého impulsu) a konečně jako měřidlo napěťového impulsu. Probereme stručně všechna tato použití.

Měření proudu představuje základní a nejdůležitější typ použití studovaného přístroje. Předpokládejme, že v časovém okamžiku t = 0 zapneme do cívky mě­řicího přístroje měřený, časově neproměnný proud I. Cívka systému se účinkem momentu D _m počne vychylovat ze své rovnovážné polohy α  = 0. Konkrétní charakter jejího pohybu bude ovšem záviset na stupni tlumení systému. Asym­ptotické řešení pohybové rovnice (4.124) pro t ℜ →  ℜ nekonecno však bude na tlumení nezá­vislé. Z rovnice (4.124) je zřejmé, že za dostatečně dlouhou dobu po zapnutí proudu zaujme novou, časově neproměnnou polohu charakterizovanou výchylkou

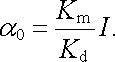(4.126)

Z výsledku (4.126) plyne, že výchylka α ₀ je přímo úměrná protékajícímu prou-du I. Magnetoelektrický měřicí přístroj má tedy lineární stupnici, což předsta­vuje jednu z jeho nejdůležitějších předností. Z praktického hlediska je žádoucí, aby tlumení systému bylo blízké kritickému stavu, v němž systém zaujme nej­rychleji novou rovnovážnou polohu. U méně citlivých robustnějších přístrojů je tohoto stavu dosaženo vhodnou konstrukcí pohyblivých částí. Tlumicí účinek proudů indukovaných ve vlastním obvodu přístroje při pohybu cívky je v tomto případě zanedbatelný a kritický aperiodický stav je v zásadě nezávislý na odporu obvodu, do kterého je přístroj zapojen. U citlivých přístrojů (galvanometrů) je naopak příspěvek proudů indukovaných ve vlastním obvodu dominantní a pro dosažení kritického aperiodického stavu je třeba dodržet určitou, konstrukcí přístroje jednoznačně určenou, hodnotu celkového odporu obvodu, do kterého přístroj zapojujeme. Tento tzv. aperiodický odpor musí být spolu s dalšími pa­rametry (vnitřní odpor cívky, citlivost, perioda vlastních kmitů T₀) výrobcem udán. Uvedené parametry určují užitné vlastnosti přístroje.

Měření náboje (proudového impulsu) tvoří další způsob klasické a dříve hojně užívané aplikace magnetoelektrického systému. Přístroj určený pro tento typ měření se obvykle nazývá balistický galvanometr. Podmínkou pro možnost měření celkového náboje prošlého v daném časovém intervalu τ  ℜ ≡  (0, τ ) cívkou přístroje je τ  <<  T₀. Je-li tato podmínka splněna, můžeme předpokládat, že celý měřený náboj projde cívkou přístroje dříve, než se cívka stačí znatelně vychýlit ze své klidové polohy. Předpokládáme-li dále platnost počátečních podmínek α  = 0, d α /dt  = 0 pro t = 0, můžeme pohybovou rovnici (4.124) jednoduše inte­grovat. Platí

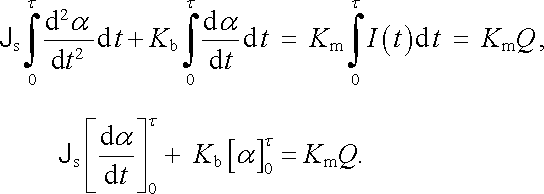Uplatníme-li uvedené počáteční podmínky a předpoklad α  B  0 pro t = τ , dosta­neme výsledek

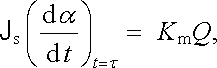(4.127)

který ukazuje, že celkový moment hybnosti (popř. maximální úhlová rych­lost) udělený proudovým impulsem měřicímu systému je za uvedených předpo­kladů úměrný celkovému prošlému náboji.

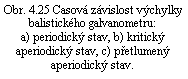
Jak jsme viděli v předchozím výkladu, z mechanického hlediska představuje měřicí systém magnetoelektrického přístroje torzní kyvadlo. Jeho maximální výchylka α _max je úměrná úhlové rychlosti, kterou systém má při průchodu rovnovážnou polohou. Podle (4.127) tedy lze psát

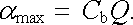(4.128)

Maximální výchylka α _max měřicího systému tedy může být využita k měření prošlého náboje Q. Konstanta C_b se nazývá balistická konstanta přístroje.

Pro měření náboje může být použit systém v periodickém i aperiodickém stavu. Časový průběh výchylky v jednotlivých režimech je kvalitativně zobrazen na obr. 4.25. Pro měření se obvykle využívají první maximální výchylky, které jsou vyznačeny na obrázku. Je zřejmé, že hodnota balistické konstanty závisí na stupni tlumení. Je proto třeba balistickou konstantu určovat vždy pro dané za­pojení s daným celkovým odporem obvodu. Dále je zřejmé, že pro měření ná­boje se hodí zejména přístroje s dlouhou periodou vlastních kmitů T₀. Přístroje používané pro tento účel v praxi mají zpravidla T₀ ℜ ≥  10  s.

Měření napěťového impulsu. V odstavci 4.1.2c bylo ukázáno, že při změně magnetického toku cívkou projde příslušným obvodem elektrický náboj, který je úměrný této změně toku. Balistický galvanometr může být tedy použit k měření změny magnetického toku, je-li tato změna dostatečně rychlá ve srovnání s do­bou vlastních kmitů T₀ přístroje. Magnetoelektrický měřicí systém však dovoluje ještě další způsob použití, který není závislý na rychlosti změny. Pro tento účel se dříve konstruovaly speciální přístroje se zanedbatelným direkčním momen­tem, které se z důvodů uvedených níže nazývají fluxmetry.

Předpokládejme, že uvedený přístroj je zapojen v obvodu, ve kterém po urči­tou omezenou dobu působí časově proměnné elektromotorické napětí E (t) . Označíme-li R_c celkový odpor obvodu a zanedbáme-li jeho indukčnost, bude okamžitá hodnota proudu tekoucího cívkou přístroje rovna I(t) =  E (t)/ R_c. Cívka se účinkem tohoto proudu vychýlí ze své původní polohy. Její pohyb se však bude utlumovat působením tlumicích mechanismů systému a přestane-li elektromotorické napětí působit, cívka se po určité době zastaví v nové poloze. Za uvedených podmínek lze pohybovou rovnici (4.124) opět jednoduše integro­vat v časovém intervalu Δ t = t₂ - t₁ , na jehož počátku i konci je měřicí systém v klidu, přičemž měřicí cívka změnila svoji polohu o úhel Δ α . Platí

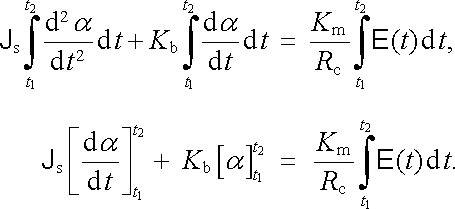Celková výchylka přístroje Δ α  =  α (t₂) -  α (t₁) je tedy úměrná napěťovému impulsu působícímu v obvodu, v podstatě nezávisle na době po kterou napětí působí, neboť z právě získaného výsledku dostáváme

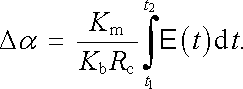(4.129)

Vztah (4.129) platí ovšem přesně pouze za předpokladu, že direkční moment systému je skutečně nulový. Ve skutečnosti však nelze otočné uložení cívky s přívody o absolutně nulovém direkčním momentu realizovat. Proto v závislosti na jakosti konstrukce daného přístroje existuje určité omezení shora pro časový interval měření Δ t .

Právě popsaná metoda se nejčastěji užívala pro měření magnetického toku či jeho změn, přičemž měřený napěťový impuls vznikal při změně magnetického toku měrnou cívkou (srov. odstavec 4.1.2c). Vzhledem k tomu, že dnes existují jiné a přesnější metody pro měření magnetického pole a magnetického toku, má právě popsané použití magnetoelektrického systému spíše jen historický vý­znam.

Naproti tomu jeho použití pro měření proudu a do jisté míry i použití pro měření proudového impulsu si přes bouřlivý rozvoj nových elektronických a číslicových metod svůj význam zachovává. Pro podrobnější poučení o kon­strukci jednotlivých typů přístrojů, jejich parametrech a konkrétních způsobech použití odkazujeme na citovanou literaturu, především [5].

---

---