---

---

4.1 Elektromagnetická indukce

4.1.1 Zákon elektromagnetické indukce

Zákon elektromagnetické indukce vyjadřuje (vedle silových účinků) další fyzi­kální projev magnetického pole. Objevil jej M. Faraday v r. 1831 na základě svých experimentů které ukázaly, že v uzavřeném elektrickém obvodu vzniká proud, jestliže v jeho okolí dochází k jakýmkoliv změnám magnetického pole.

Jev elektromagnetické indukce je možné studovat v několika situacích. Uva­žujme vodivou uzavřenou smyčku zhotovenou z homogenního vodiče, která je umístěna v blízkosti zdrojů magnetického pole. (Tyto zdroje mohou být libo­volné a mohou být tudíž tvořeny jakoukoliv soustavou vodičů protékaných proudem a zmagnetovaných těles.) Předpokládejme dále, že máme možnost mě­řit proud protékající smyčkou. Zjistíme, že smyčkou nepoteče žádný proud, jest­liže magnetické pole v jejím okolí bude neproměnné a smyčka bude v klidu. Naopak smyčkou počne protékat proud:

a) jestliže se smyčka počne vhodným způsobem pohybovat,

b) jestliže se vhodným způsobem počnou pohybovat zdroje magnetic­kého pole,

c) jestliže smyčka i zdroje magnetického pole zůstanou v klidu vůči labora­torní (pozorovací) soustavě, ale počne se měnit magnetické pole uvnitř smyčky (na­příklad tím, že se změní proudy v některých vodičích vytvářejících pole).

Výsledky experimentů ukazují, že na nositele proudu ve vodiči smyčky pů­sobí ve všech uvedených případech síly, které jsou schopny vyvolat proud. Po­dobně jako v čl. 3.2.3 je i zde výhodné popsat vzniklou situaci zavedením pří­slušné vtištěné intenzity 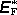a jí příslušného elektromotorického napětí, které nazýváme indukované elektromotorické napětí E _F. Na rozdíl od stacionárních soustav vyšetřovaných v předchozí kapitole, kdy mohlo elektromotorické napětí působit jen v nehomogenních vodičích, může indukované elektromotorické na­pětí vznikat při změnách magnetického pole i ve vodičích homogenních. Ozna­číme-li tedy R celkový odpor smyčky a I(t) okamžitou hodnotu v ní indukova­ného proudu, můžeme v analogii se vztahem (3.30) definovat okamžitou ho-dnotu indukovaného elektromotorického napětí E _F(t) pomocí rovnice

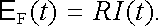(4.1)

Na základě podrobnějších pokusů s elektromagnetickou indukcí bylo uká­záno, že pro vznik indukovaného elektromotorického napětí jsou určující změny celkového magnetického toku procházejícího plochou smyčky. Z výsledků uvedených pokusů je možné stanovit kvantitativní vztah mezi hodnotou E _F(t) a těmito změnami toku:

Velikost indukovaného elektromotorického napětí je rovna velikosti totální časové derivace celkového magnetického toku smyčkou. Směr indukovaného proudu ve smyčce je vždy takový, že magnetické pole vytvořené tímto proudem se vždy snaží kompenzovat změny toku odpovědné za vznik indukovaného proudu. (Poznatek o směru indukovaného proudu se v literatuře často nazývá Lenzovo pravidlo.) Právě uvedené závěry se obvykle vyjadřují ve tvaru[30]

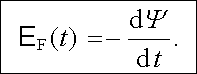(4.2)

Vztah (4.2) vyjadřuje správnou hodnotu indukovaného elektromotorického na­pětí nezávisle na tom, jakým způsobem změny toku nastávají. Jeho platnost je experimentem plně potvrzena ve všech uvedených případech (a) až (c) a také tehdy, probíhají-li tyto změny najednou.

Vzniká ještě otázka jednoznačnosti určení magnetického toku. Magnetický tok Ψ v (4.2) je totiž dán relací (3.59) , v níž plocha S představuje plochu použité smyčky, jejíž volba není jednoznačná. (V případě smyčky ve tvaru kružnice může být například za její plochu považována plocha příslušného kruhu, nebo část kulové plochy procházející smyčkou, nebo dokonce libovolná plocha ohra­ničená uvažovanou smyčkou.) Zákon elektromagnetické indukce vyjádřený vztahem (4.2) bude mít jednoznačný fyzikální smysl jedině tehdy, bude-li hod­nota magnetického toku Ψ nezávislá na tom, kterou z možných ploch S ohrani­čených uvažovanou smyčkou pro výpočet podle (3.59) zvolíme.

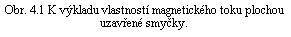
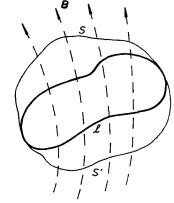
Uvedená vlastnost magnetického toku bude automaticky splněna, budeme-li předpokládat, že i pro kvazistacionární pole zůstává v platnosti vztah (3.72) , podle něhož je celkový magnetický tok procházející libovolnou uzavřenou plo­chou nulový. Daná plocha S ohraničená uzavřenou smyčkou l může být totiž vždy doplněna jinou libovolně vybranou plochou S ℜ' (rovněž ohraničenou křiv­kou l) na uzavřenou plochu S + S ℜ' (viz obr. 4.1). Z nulovosti magnetického toku plochou S + S ℜ' pak ihned plyne rovnost magnetických toků plochami S a S ℜ' . Magnetický tok procházející danou smyčkou bude tedy za uvedeného předpo­kladu jednoznačně určen jen její velikostí, tvarem a polohou v prostoru.

Vztah (3.72) představuje jednu ze základních vlastností magnetického pole i v kvazistacionárním přiblížení. Vyjadřuje skutečnost, že i v kvazistacionárním magnetickém poli jsou magnetickými indukčními čárami vždy uzavřené křivky. (Obecné vlastnosti kvazistacionárního pole budou diskutovány v čl. 4.1.3.)

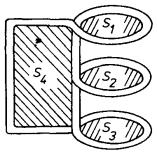
Při používání vztahu (4.2) je důležité si uvědomit, že tok Ψ musí být skutečně celkový magnetický tok procházející danou smyčkou. Na tuto okolnost je třeba dát pozor zejména tehdy, má-li použitý obvod složitější tvar. Na obrázku 4.2 je uveden příklad smyčky tvořené třemi kruhovými závity spojenými do zkratu. Celkový magnetický tok procházející touto smyčkou je dán například součtem toků tekoucích plochami S₁ až S₄.[31]

Při výkladu zákona elektromagnetické indukce jsme předpokládali, že všechna měření jsou prováděna ve vztažné soustavě pevně spojené s laboratoří. Pozorovatel pracující v této soustavě může považovat magnetické pole za funkci polohového vektoru a času B  ℜ ≡  B ( r , t) . Časová závislost vektoru magnetické indukce v daném bodě může být způsobena jednak změnou proudů ve vodičích tvořících zdroje magnetického pole a jednak pohybem těchto vodičů vůči labo­ratorní soustavě. Pozorovatel pracující v této soustavě nemusí mít vždy možnost rozlišit, kterou z uvedených možností jsou změny magnetického pole vyvolány. Elektromotorické napětí indukované ve smyčce l nehybné vůči laboratorní sou­stavě je možné vyjádřit speciálnějším vzorcem

.

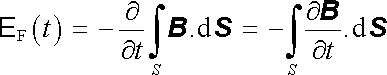(4.3)

Zdůrazněme ještě jednou, že tento poslední výraz neplatí na rozdíl od (4.2) obecně; zahrnuje pouze uvedené případy (b), (c). V případě, kdy smyčka koná pohyb vůči laboratorní soustavě, je nutné započíst ještě změny toku způsobené změnou polohy (popř. i velikosti a tvaru) plochy S.

Existence indukovaného elektromotorického napětí je jednou z příčin, že zákonitosti platné pro stacionární elektrické obvody (viz články 3.2.3 a 3.2.4) v kvazistacionárním přiblížení obecně neplatí. Pojem elektrického obvodu musí být zobecněn a musí být rovněž zobecněny příslušné vztahy popisující jeho vlastnosti. Docházíme k pojmu kvazistacionárního elektrického obvodu, jehož vlastnostmi se budeme zabývat ve oddílu 4.2.

Vzhledem k tomu, že zákon elektromagnetické indukce představuje vedle silových účinků druhý, z hlediska klasické fyziky nezávislý fyzikální projev magnetického pole,[32] může být vztah (4.2) stejně dobře jako Lorentzův vzorec (3.56) použit k definici vektoru magnetické indukce. Vyjadřování magnetického toku ve voltsekundách, které bylo zmíněno v čl. 3.3.1, je tedy s ohledem na vztah (4.2) plně fyzikálně oprávněno.

4.1.2 Souvislost mezi elektromagnetickou indukcí a silovými účinky
magnetického pole

Proberme nyní několik typických experimentálních situací, v nichž se projevuje jev elektromagnetické indukce.

a) Pohyb přímého vodiče v homogenním magnetickém poli

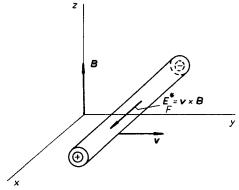
Uvažujme vodivou tyč orientovanou podél osy x dané inerciální soustavy sou­řadné. Nechť se tyč pohybuje ve směru osy y v homogenním magnetickém poli B orientovaném ve směru osy z (viz obr. 4.3). Podle Lorentzova vzorce bude na volné nositele náboje ve vodiči působit síla, která bude mít tendenci posunovat náboje různého znamení opačným směrem. Ve smyslu výkladu předchozího článku lze toto silové působení popsat vtištěnou intenzitou 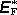, pro níž bude podle (3.56) platit

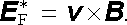(4.4)

Účinkem tohoto silového pole se bude tyč na jednom konci nabíjet kladně a na druhém konci záporně, takže uvnitř vodiče vznikne elektrické pole E . Rovno­vážný stav nastane, vykompenzuje-li toto elektrické pole vtištěnou intenzitu 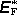, tedy

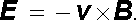(4.5)

Z výsledku vidíme, že v dané situaci vzniká uvnitř pohybujícího se vodiče elek­trické pole, které je důsledkem silových účinků magnetického pole na pohybující se náboje. Jev elektromagnetické indukce je tedy v tomto speciálním případě důsledkem silových účinků magnetického pole.

Je zajímavé si uvědomit, jakou situaci bude sledovat pozorovatel v soustavě souřadnic pevně spojené s vodičem. V této soustavě jev elektromagnetické in­dukce nenastává, neboť vodič je v homogenním poli v klidu. Elektrické pole E uvnitř vodiče musí tedy vymizet. To skutečně nastane, neboť v nové soustavě bude působit elektrické pole E ℜ'  = v  ℜ ×  B , které vznikne transformací původního magnetického pole (srov. příklad 2.2.5d). Náboje na povrchu vodiče můžeme považovat za důsledek působení tohoto elektrického pole. Výsledné elektrické pole uvnitř vodiče pak bude skutečně nulové.

b) Princip elektrického stroje

Vyšetřeme podmínky pro vznik elektrického proudu v uzavřené smyčce, který je důsledkem elektromagnetické indukce ve vodiči, pohybujícím se v magnetickém poli. Uvažujme vodivou smyčku ve tvaru obdélníka, zhotovenou z homogenního vodiče vyhovujícího Ohmovu zákonu, jejíž jedna strana p je pohyblivá (viz obr. 4.4a). Smyčka nechť je vložena do homogenního magnetického pole B kolmého k její rovině a mířícího za nákresnu.

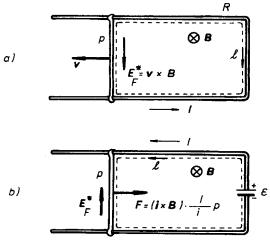
Bude-li se příčka p pohybovat účinkem vnější síly rychlostí v , nastane v ní situace stejná jako ve vodiči vyšetřovaném v předchozím odstavci. Na volné nositele náboje bude působit vtištěná intenzita 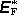podle (4.4) , která může zřejmě nahradit vtištěnou intenzitu E ^* ve vztahu (3.26) vyjadřujícím Ohmův zákon pro nehomogenní vodiče. Integrací tohoto výrazu podél celé smyčky lze vypočítat proud I tekoucí smyčkou (srov. postup, kterým byl získán vztah (3.30) ). Platí

.

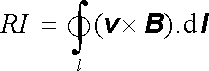(4.6)

Veličina na pravé straně má význam indukovaného elektromotorického napětí E _F . Jelikož 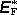je od nuly různé pouze podél příčky p, platí

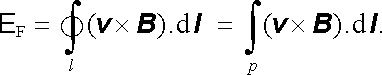(4.7)

Vzorec pro indukované napětí E _F lze dále upravit. Jelikož je 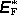konstantní po­dél celé příčky, dostaneme jednoduchý výraz

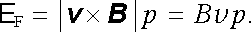(4.8)

Elektromotorické napětí E _F v (4.8) je kladná veličina, neboť jsme směr integrace volili souhlasně se směrem 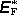, a tedy i se směrem proudu I. Lze snadno vyjádřit E _F ve tvaru obecného vzorce pro elektromagnetickou indukci (4.2) . Součin v p představuje totiž plochu, kterou opíše příčka p za jednotku času. Veličina Bv p pak zřejmě udává absolutní hodnotu změny magnetického toku smyčkou připa­dající na jednotku času. Jelikož pro výpočet celkového magnetického toku Ψ smyčkou musíme ponechat orientaci její plochy danou směrem protéka­jícího proudu, je - jak plyne z obr. 4.4a - tento tok záporný. Je tedy E _F  =  B v p  = - Δ Ψ /Δ t , což je hledaný tvar (4.2) .

Proud protékající obvodem vyvolává ve vodičích vznik Jouleova tepla. Energii potřebnou pro vznik tohoto tepla dodává vnější síla, která při pohybu příčky koná práci. Vidíme tedy, že jev elektromagnetické indukce umožňuje, aby v uvažovaném obvodu podle obr. 4.4a mohla být mechanická práce měněna na elektrickou energii.

Můžeme také vyšetřovat obrácený děj podle obr. 4.4b. Do smyčky nechť je zapojen vnější zdroj elektromotorického napětí E , který v ní vzbudí proud I. Na vodiče smyčky počne opět působit podle (3.58) síla. Předpokládejme, že jako v předchozím případě je smyčka pevná a pouze příčka p je pohyblivá. Příčka p se pak může účinkem síly F pohybovat a soustava je schopna konat mechanic­kou práci. Označíme-li rychlost příčky v  ℜ' , bude práce vykonaná za jednotku času zřejmě rovna

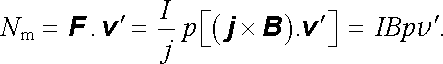(4.9)

Tato práce je konána na úkor energie dodané soustavě zdrojem elektromotoric­kého napětí E . Podle (3.48) je výkon dodaný tímto zdrojem do obvodu roven N_z = E I. Předpokládáme-li, že kromě zmíněné mechanické práce a Jouleova tepla neprobíhají v obvodu žádné procesy podílející se na energetické bilanci, můžeme na základě zákona zachování energie psát

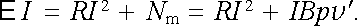(4.10)

Podle (4.8) však Bpv ' představuje absolutní hodnotu elektromotorického napětí 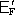, které se v příčce indukuje při jejím pohybu. Chceme-li vnější elektromoto­rické napětí považovat za kladnou veličinu, musíme za kladný směr integrace považovat směr proudu I. Pak ovšem

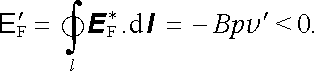Po dosazení do (4.10) můžeme energetickou bilanci v obvodu zapsat také ve tvaru

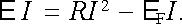(4.11)

O poměrech v obvodu máme tedy tento výsledný obraz. Vnější zdroj elektro­motorického napětí budí v obvodu proud, který vyvolává silové účinky na vodič p. Počne-li se vodič v důsledku těchto sil pohybovat, počne soustava konat me­chanickou práci. V pohybující se smyčce se indukuje elektromotorické napětí E _F , které působí proti vnějšímu napětí E , a způsobí tedy zmenšení proudu. Jeho konečná hodnota je dána vztahem (4.11) . Mechanická práce konaná při pohybu vodiče je konána na úkor energie dodané vnějším zdrojem elektromoto­rického napětí. Jelikož lze práci vykonanou za jednotku času vyjádřit ve tvaru -E _FI , můžeme také říci, že energie dodávaná vnějšími zdroji se spotřebovává na udržování proudu proti směru indukovaného elektromotorického napětí. Rozbor situace v tomto obvodu ukázal, že vznik indukovaného elektromotorického na­pětí je podstatný činitel umožňující proměnu elektrické energie v mechanickou práci.

Soustava na obrázku 4.4b popisuje fyzikální princip elektromotoru, zatímco soustava na obr. 4.4a princip elektrického generátoru. Z provedených úvah vy­plývá, že silové účinky na pohybující se vodič a indukování elektromotorického napětí v pohybujícím se vodiči představují dvě různé stránky obecnějšího fyzi­kálního projevu magnetického pole. Existence silových účinků magnetického pole podmiňuje existenci elektromagnetické indukce a naopak. Každý elektro­motor může principiálně sloužit jako generátor (je-li z vnějších zdrojů dodávána mechanická práce) a obráceně každý generátor může sloužit jako elektromotor (je-li dodávána elektrická energie z vnějších zdrojů elektromotorického napětí).

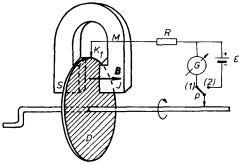
Na obrázku 4.5 je znázorněno principiální uspořádání jednopólového elektrického stroje s otáčivým pohybem (tzv. Barlowovo kolečko), který do značné míry věrně realizuje fyzikální situaci právě popsaných experimentů, viz obr. 4.4, a tudíž se často používá k demonstraci činnosti generátoru i elektro­motoru. Vodivý (nejčastěji měděný) disk D upevněný na otočném hřídeli je umístěn mezi póly trvalého magnetu M. Při otáčení hřídelem můžeme měřicím přístrojem G detekovat indukovaný proud (přepínač P v poloze (1). Naopak zapojíme-li do obvodu vnější zdroj elektromotorického napětí E tak, aby obvo­dem protékal proud stejného směru (přepínač P v poloze (2)), počne se kolečko otáčet opačným směrem.

c) Princip fluxmetru

Fluxmetrem je nazýván klasický přístroj, který se dříve hojně užíval k měření magnetického pole. Přístroj byl založen na možnosti převést měření změny mag­netického toku plochou vodivé smyčky na měření náboje prošlého obvodem, v němž je smyčka zapojena. I když se tento přístroj dnes téměř nepoužívá, je užitečné se seznámit s jeho principem, který velmi dobře demonstruje vlastnosti elektromagnetické indukce.

Uvažujme rovinnou cívku o N závitech umístěnou ve vnějším magnetickém poli B , dostatečně malého průřezu S tak, abychom v celém jejím objemu mohli magnetické pole považovat za homogenní. Nechť je cívka zapojena do obvodu o celkovém odporu R spolu s měřidlem umožňujícím měřit celkový prošlý náboj q. (O klasické možnosti měření prošlého náboje pomocí balistického galvano­metru pojednává příklad 4.3.4d.) Předpokládejme, že jsme v místě cívky jakým­koliv způsobem změnili magnetické pole z počáteční hodnoty B _i na konečnou hodnotu B _f. Ukážeme, že celkový náboj prošlý obvodem při změně pole nezávisí na charakteru této změny, ale jen na počáteční (Ψ _i ) a konečné (Ψ _f ) hodnotě magnetického toku procházejícího cívkou.

Pro počáteční a konečnou hodnotu celkového magnetického toku cívkou zřejmě platí

.

Označíme-li dále I(t) okamžitou hodnotu proudu indukovaného v obvodu cívky při změně magnetického pole, můžeme pro náboj q psát

,

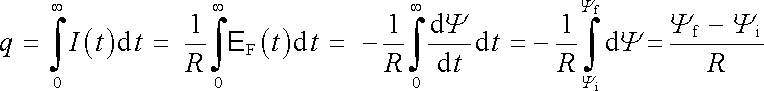(4.12)

čímž je vytčený úkol vyřešen.

V odstavcích 4.1.2a,b byla diskutována souvislost indukovaného elektro-motorického napětí a silových účinků magnetického pole. Bylo by však zá­sadně mylné považovat tyto úvahy za obecné odvození zákona elektromag­netické indukce ze silových účinků magnetického pole. Všechny uvedené úvahy se týkaly pouze indukovaného elektromotorického napětí v pohybujících se vodičích za předpokladu, že magnetické pole je vůči pozorovací vztažné sou­stavě časově neproměnné .

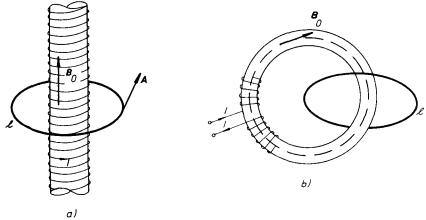
Obr. 4.6 Demonstrace elektromagnetické indukce ve smyčce umístěné v prostoru s nulovou magnetickou indukcí: a) smyčka obepínající nekonečně dlouhý solenoid, b) smyčka obepínající toroid.

Zákon elektromagnetické indukce, tak jak byl formulován v předchozím článku, představuje mnohem obecnější poznatek. Z hlediska klasické fyziky musí být považován za nový fyzikální zákon formulovaný na základě experi­mentu. Skutečnost, že jev elektromagnetické indukce nemůže být vždy vyložen na základě silových účinků magnetického pole na pohybující se náboje, lze de­monstrovat pomocí myšlenkového experimentu podle obr. 4.6a. Uvažujme kru­hovou vodivou smyčku l poloměru r, obepínající nekonečně dlouhý solenoid o poloměru a < r. Tato smyčka prochází celá prostorem s nulovou magnetickou indukcí, takže magnetické pole vytvořené solenoidem nemůže na nositele proudu ve smyčce silově působit ve smyslu vztahu (3.57) . Přesto však, platí-li zákon elektromagnetické indukce, bude se při změně proudu cívkou solenoidu ve smyčce indukovat proud, neboť se bude měnit magnetický tok tekoucí plo­chou smyčky. Pro okamžitou hodnotu elektromotorického napětí indukovaného ve smyčce E _F(t) platí podle (4.3) a podle výsledků příkladů 3.3.5e

.

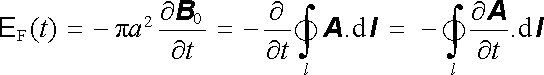(4.13)

Získaný výsledek ukazuje zároveň, že má reálný fyzikální smysl uvažovat vekto­rový potenciál i v těch částech prostoru, ve kterých je magnetická indukce nu­lová. (K diskusi o této otázce se ještě vrátíme v kapitole 6.) Uvedený experiment lze za téměř ideálních podmínek realizovat v uspořádání podle obr. 4.6b, kdy je nekonečný solenoid nahrazen toroidem (srov. příklad 3.3.5d).

Otázka vzájemné souvislosti silových účinků magnetického pole a jevu elektromagnetické indukce se ovšem jeví v jiném světle z hlediska relativistické fyziky. V kapitole 2 bylo například ukázáno, že alespoň v některých speciálních situacích je možné magnetické pole se všemi jeho projevy chápat jako specifický důsledek Coulombova zákona, svázaný s danou inerciální soustavou souřadnou.

4.1.3 Obecné vlastnosti kvazistacionárního pole

Jak bylo již naznačeno v úvodu této kapitoly, v kvazistacionárním přiblížení připouštíme "pomalé" časové změny příslušných charakteristik soustavy. Přede­vším je možné, aby se s časem měnilo rozložení makroskopických nábojů v prostoru, což znamená, že objemová hustota volných nábojů ρ ( r ,   t) i obje-mová hustota vázaných nábojů ρ _p( r ,   t) mohou být explicitní funkce času. "Pomalost" časových změn objemové hustoty volných nábojů je dána požadav­kem, aby druhý člen 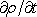v obecné rovnici kontinuity proudu (3.15) byl zane­dbatelný proti členu prvnímu, takže proudová hustota volných proudů j ( r ,   t) splňuje rovnici kontinuity (3.16)

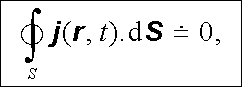popř. (3.17)

která je charakteristická pro stacionární soustavy. Je rovněž zřejmé, že v kvazi-stacionárním přiblížení se málo uplatní vázané proudy, včetně posuvného proudu v dielektrikách, jehož proudová hustota je dána časovou derivací vektoru polarizace (srov. vztah (3.12) ).

Časově závislé rozložení nábojů budí v okolním prostoru časově proměnné elektrické pole. Kvazistacionární elektrické pole je tedy obecně závislé na čase. Experimentální zkušenost ukazuje, že je v řadě konkrétních případů můžeme s dobrou přesností považovat za pole potenciální. Intenzita kvazistacionárního elektrického pole E ( r ,   t) tedy v každém okamžiku splňuje podmínku (1.61)

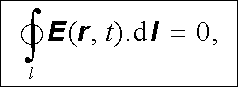respektive podmínku (1.63)

Skalární potenciál φ ( r ,   t) (obecně rovněž časově závislý) je definován známou relací (1.50)

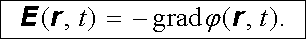Kvazistacionární elektrické pole splňuje rovněž Gaussův zákon. V přítomnosti látkového prostředí lze zavést vektor elektrické indukce vztahem typu (1.246) D ( r ,   t) =  ε ₀ E ( r ,   t) +   P ( r ,   t) . Platí pak vztah (1.247)

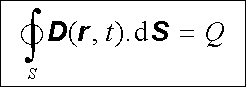nebo v diferenciálním tvaru vztah (1.248)

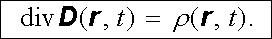Uvedené vlastnosti elektrického kvazistacionárního pole jsou, jak vidíme, fo­málně shodné s vlastnostmi pole stacionárního. V kapitole 5 uvidíme, že poten­ciální charakter kvazistacionárního elektrického pole je důsledkem určité nedů­slednosti v aplikaci zákona elektromagnetické indukce a představuje jen určité přiblížení. Veškerá elektrotechnická praxe však ukazuje užitečnost tohoto přiblí­žení, které je s dostatečnou přesností schopné popsat velkou třídu technicky důležitých situací. Přesto však, že elektrické stacionární a kvazistacionární pole jsou popsána formálně shodnými rovnicemi, existují rozdíly v působení obou polí na nabitou částici. I když například pro kvazistacionární pole v každém okamžiku platí vztah (1.61) , může (vzhledem k časové závislosti pole) nabitá čás-tice, pohybující se po uzavřené dráze konečnou rychlostí, konat nenulovou práci.

V úvodu oddílu 3.3 bylo zmíněno úsilí fyziků na přelomu devatenáctého a dvacátého století prokázat experimentálně ekvivalenci magnetických účinků všech mechanismů elektrického proudu. Navzdory pozitivním výsledkům těchto experimentů se v kvazistacionárním přiblížení (vzhledem k jeho charakteru při­pouštějícímu jen "pomalé" časové změny) zcela zanedbávají magnetické účinky posuvných proudů. V příští kapitole uvidíme, že tato aproximace podstatnou měrou ochuzuje popis elektromagnetických jevů.

Při zanedbání magnetických účinků polarizačních proudů v látkách nastane podobná situace jako ve stacionárním přiblížení. Za zdroje magnetického pole mohou být (vedle zmagnetovaných látek) považovány jen volné proudy, takže je přirozené předpokládat platnost Amp`erova zákona ve formálně stejném tvaru. Vlastnosti kvazistacionárního magnetického pole, které z tohoto předpokladu plynou, jsou v plné shodě s výsledky příslušných experimentů. (Možnosti de­monstrace platnosti Amp`erova zákona pro kvazistacionární pole v relativně obecném uspořádání popisuje příklad 4.1.5a.)

Pro obecnou situaci kvazistacionárního pole v látkách, které může být časově závislé, lze vedle magnetické indukce B ( r ,   t) zavést intenzitu magnetického pole H ( r ,   t) . Amp`erův zákon v integrálním tvaru lze pak vyjádřit podmínkou (3.137)

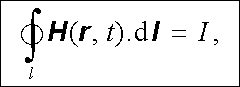v níž I je celkový volný proud protékající plochou uzavřené křivky l, a jeho dife­renciální tvar je dán rovnicí (3.138)

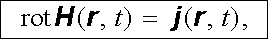v níž j ( r ,   t) je hustota volného proudu.

Z platnosti Amp`erova zákona a rovnice kontinuity ve speciálním tvaru (3.16) , popř. (3.17) , plyne dále možnost zavedení vektorového potenciálu A ( r ,   t) definičním vztahem (3.74) , který splňuje kalibrační podmínku (3.76) div  A ( r ,   t) = 0 . Odtud plyne, že pro kvazistacionární pole zůstávají v platnosti všechny závěry článku 3.3.3. Speciálně v každém bodě platí vztah (3.73)

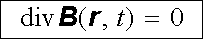a pro libovolnou uzavřenou plochu S je, viz (3.72) ,

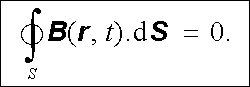Podmínky potřebné pro jednoznačnou formulaci zákona elektromagnetické in­dukce jsou tedy skutečně splněny.

Právě vyložené vlastnosti elektrického a magnetického kvazistacionárního pole je samozřejmě třeba doplnit zákonem elektromagnetické indukce formulo­vaným vztahem (4.2)

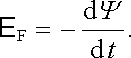Tento zákon přináší jednu z nejpodstatnějších nových kvalit kvazistacionárního pole ve srovnání s polem stacionárním. Ze zákona elektromagnetické indukce plyne, že časové změny magnetického pole vyvolávají změny v rozložení elek­trických nábojů, a tedy i změny elektrického pole. Tyto změny elektrického pole mohou naopak vyvolat změny v rozložení proudu, a tedy zpětně i změny mag­netického pole. Elektrické a magnetické pole přestávají být tedy navzájem nezávislé.

Pro kvazistacionární pole lze v mnoha případech zachovat platnost materiálo­vých vztahů tak, jak byly vyloženy v kapitolách l a 3. Speciálně v mnoha přípa­dech lze charakterizovat vlastnosti prostředí jeho permitivitou, permeabilitou a měrnou vodivostí, přičemž pro nepříliš rychlé změny pole lze tyto veličiny po­važovat za konstanty. Při používání Ohmova zákona však musíme mít na pa­měti, že na nositele proudu může působit navíc indukovaná vtištěná intenzita 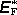, o kterou je třeba doplnit jeho obecnou formulaci (3.26) . Ani pro homogenní vodič nelze obecně užívat Ohmův zákon v prostém tvaru (3.22) , takže v kvazi-stacionárním poli neplatí obecně důsledky (3.24) , (3.25) . Při vhodném úplatnění elektromagnetické indukce může být i v homogenním prostředí nenulová hustota volných či vázaných nábojů.

Z matematického hlediska je kvazistacionární elektrické a magnetické pole popsáno formálně totožnými rovnicemi jako stacionární elektrické a stacionární magnetické pole. Fyzikální odlišnost kvazistacionárního pole je vyjádřena ji­nými okrajovými podmínkami, které musí brát v úvahu navíc pole indukované vtištěné intenzity .

4.1.4 Vlastní a vzájemná indukčnost vodičů

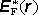Uvažujme vodivou smyčku protékanou proudem I(t) , která je uložena ve vakuu. Jak plyne z (3.82) , je magnetické pole B ( r ,   t), v daném bodě vybuzené touto smyčkou, lineární funkcí proudu I(t) . Směr vektoru B zůstává v každém bodě stálý; se změnami proudu se mění pouze jeho velikost. Magnetický tok Ψ libo­volnou plochou S je proto také lineární funkcí proudu I. Tato linearita zůstane zřejmě zachována i v případě, kdy bude prostor vyplněn hmotným prostředím, jehož permeabilita (resp. magnetická susceptibilita) není závislá na magnetickém poli. (Podle čl. 3.5.4 bude tato linearita dobře zachována v případě paramagne­tických a diamagnetických látek. Pro feromagnetické látky bude naopak vztah mezi magnetickým tokem a proudem I obecně nelineární.)

Uvažujme nyní speciální případ, kdy za plochu S zvolíme některou z ploch ohraničenou uvažovanou proudovou smyčkou l (srov. obr. 4.1). Mezi magnetic­kým tokem Ψ tekoucím touto plochou a proudem I bude zřejmě platit vztah

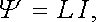(4.14)

ve kterém konstanta úměrnosti L, která se nazývá vlastní indukčností smyčky, je závislá pouze na geometrickém tvaru smyčky, popřípadě na permeabilitě pro­středí vyplňujícího prostor.

Vlastní indukčnost vodiče vyjadřuje jeho schopnost vytvářet magnetické pole. Jde tedy o veličinu, která je v jistém smyslu analogická kapacitě vodiče (srov. článek 1.4.5). Pro správné pochopení definičního vztahu (4.14) je třeba si uvědomit, že magnetický tok Ψ představuje skutečně celkový magnetický tok vytvořený smyčkou, podobně jako při formulaci zákona elektromagnetické indukce (srov. obr. 4.2).

Vlastní indukčnost může být zavedena nejen pro uzavřenou smyčku koneč­ných rozměrů, ale i pro libovolný vodič či jeho úsek. Při definici je třeba opět dbát na to, aby v definičním vztahu vystupoval celkový magnetický tok vytvo­řený uvažovaným úsekem. Například v případě dvojice přímých nekonečně dlouhých vodičů bude celkový magnetický tok vytvořený úsekem délky protékat vyšrafovanou plochou na obr. 4.9b. Je tedy třeba počítat nejen s tokem vně, ale i uvnitř vodičů. Výpočet indukčnosti L_d připadající na délku d vodičů je řešen v příkladu 4.1.5b.

Nyní budeme věnovat pozornost obecnějšímu problému. Nechť je v prostoru rozmístěno N smyček l₁, l₂,..., l_N, protékaných proudy I₁, I₂,..., I_N. Je zřejmé, že celkový magnetický tok Ψ _i, protékající i-tou smyčkou, bude obecně záviset na proudech ve všech uvažovaných N smyčkách. Podle toho co bylo řečeno na začátku článku je dále zřejmé, že příspěvek Ψ _ik k-té smyčky k celkovému toku Ψ _i bude možné vyjádřit vztahem

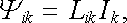(4.15)

ve kterém L_ik představuje opět veličinu závislou pouze na tvaru, velikosti, vzá­jemné poloze a orientaci příslušných smyček a na permeabilitě prostředí. Cel­kový tok Ψ _i libovolné z uvažovaných smyček (i = 1,..., N) bude tedy možné vyjádřit ve tvaru

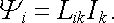(4.16)

Koeficienty se stejnými indexy L_kk (k = 1,..., N) představují zřejmě vlastní in­dukčnosti jednotlivých smyček. Koeficienty L_ik pro i ℜ ≠  k vyjadřují, jak proud v k-té smyčce přispívá k magnetickému toku i-tou smyčkou. Nazývají se vzá­jemnými indukčnostmi příslušných smyček.

Vztahy (4.14) , (4.15) a (4.16) představují tzv. statickou definici vlastní a vzájemné indukčnosti. Kromě nich se užívá také dynamických definičních vztahů, které udávají souvislost mezi indukovanými elektromotorickými napě­tími v jednotlivých smyčkách a změnami proudu. Tyto vztahy získáme snadno použitím výrazu (4.2) vyjadřujícího zákon elektromagnetické indukce. Budeme nejdříve uvažovat pouze jedinou smyčku, v níž může docházet ke změnám proudu I. Tyto změny proudu budou vyvolávat změny magnetického toku tekou­cího smyčkou, které je možné vyjádřit vztahem (4.14) . Změny magnetického toku budou dále vyvolávat ve smyčce indukované elektromotorické napětí E _F , pro které podle zákona elektromagnetické indukce dostaneme

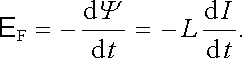(4.17)

Podobně pro uvažovanou soustavu N smyček bude elektromotorické napětí E _F,i , indukované v i-té smyčce v důsledku změn proudů I₁, I₂,..., I_N ve všech smyčkách, dáno vztahem

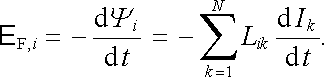(4.18)

Z energetických úvah (viz úlohu Ú 4.5) lze ukázat, že vlastní indukčnost vodiče je vždy kladná veličina. Vzájemná indukčnost může být naopak kladná i záporná v závislosti na tom, je-li (při dané orientaci příslušných ploch) příspěvek Ψ _ik v  (4.15) k celkovému toku Ψ _i kladný či záporný. Platí však obecně

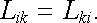(4.19)

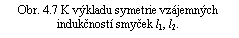
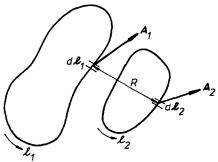
Pro dvojici smyček l₁, l₂ (například podle obr. 4.7) lze relaci (4.19) dokázat jed­noduše, vyjádříme-li magnetický tok pomocí vektorového potenciálu vztahem (3.59a) . Pro vzájemné indukčnosti smyček platí podle definice

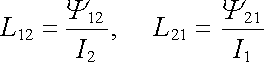(4.20)

a například pro L₁₂ dostaneme pomocí (4.20) a dále využitím (3.82)

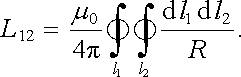(4.21)

Tento výraz je nezávislý na pořadí indexů (1) a (2), což dokazuje vztah (4.19) . Jeho platnost je možné dokázat i na základě energetických úvah - viz úlohu Ú 4.6.

Podmínka (4.19) vyjadřuje tzv. větu o vzájemnosti, kterou lze formulovat takto:

Jestliže proud I v k-tém obvodu přispívá k celkovému magnetickému toku i- tého obvodu hodnotou Ψ _ik , pak stejný proud v i-tém obvodu přispívá stejnou hodnotou magnetického toku k-tého obvodu.

V soustavě SI je jednotkou vlastní i vzájemné indukčnosti henry (H). Podle (4.14) , respektive (4.15) , platí: henry = weber/ampér = voltsekunda.ampér^-1.

4.1.5 Řešené příklady

a) Demonstrace platnosti Amp`erova zákona (měřicí transformátor)

Všimneme si konkrétního uspořádání, které umožňuje demonstrovat platnost Amp`erova zákona relativně obecným způsobem a které má také praktický vý­znam, neboť umožňuje měřit (periodicky proměnný) proud ve vodiči bez nut­nosti zařazovat měřicí přístroj do příslušného obvodu.

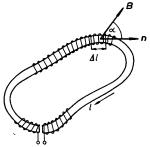
Uvažujme cívku o velkém počtu závitů navinutou na ohebném jádru malého průřezu Δ S zhotoveném z vhodného materiálu (kůže, plastická látka apod.). Z této cívky lze vytvořit uzavřenou smyčku l velmi obecného tvaru (viz obr. 4.8), přičemž lze předpokládat, že plocha každého závitu je v podstatě kolmá ke směru křivky l v daném místě.

Předpokládejme dále, že cívka je vložena do magnetického pole libovolné soustavy vodičů. Abychom mohli vypočítat celkový magnetický tok Ψ tekoucí touto cívkou, uvažujme nejdříve její malou část Δ l (viz obr. 4.8). Zavedeme jednotkový vektor n , jehož směr má směr tečny smyčky l v daném místě a jehož orientace souhlasí se zvolenou orientací smyčky. Lze pak napsat Δ l  = n Δ l, Δ S  = n Δ S. Magnetický tok Δ Φ tekoucí jedním závitem cívky vyjádříme ve tvaru Δ Φ  = B   .   Δ S . Nechť na jednotkovou délku cívky připadá 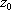závitů. Na úseku Δ l bude potom z₀Δ l závitů. Celkový magnetický tok Δ Ψ tekoucí všemi závity na úseku Δ l bude mít tvar

.

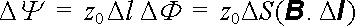Magnetický tok Ψ tekoucí celou cívkou tedy zajisté můžeme vyjádřit křivkovým integrálem

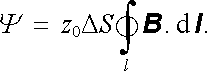(4.22)

Bude-li se magnetické pole měnit, bude se v cívce indukovat elektromotorické napětí E _F(t) , které bude mít hodnotu

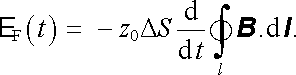(4.23)

Předpokládejme nyní, že v okamžiku t = 0 zapneme proud ve vodičích vytvářejí­cích studované magnetické pole. Proud v těchto vodičích a magnetické pole v jejich okolí začne od tohoto okamžiku narůstat, až po uplynutí dostatečně dlouhé doby dosáhne své rovnovážné hodnoty. V cívce se při tomto procesu bude indukovat elektromotorické napětí podle vztahu (4.23) . Jestliže bude cívka zapojena do uzavřeného obvodu, poteče jím proud. Snadno vypočítáme hodnotu celkového náboje Q, který proteče obvodem o celkovém odporu R po zapnutí (nebo také vypnutí) proudu ve zmíněných vodičích (srov. odstavec 4.1.2c). Zřejmě platí

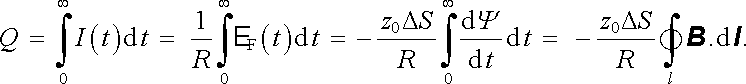(4.24)

Získaný vzorec ukazuje, že celkový náboj prošlý obvodem měrné cívky při za­pnutí pole je úměrný křivkovému integrálu (3.64) z konečných hodnot pole. Připojíme-li tedy měrnou cívku k měřicímu přístroji schopnému měřit celkový prošlý náboj, můžeme měřením pro různé polohy cívky ověřovat platnost vztahu (3.68) . Především se můžeme přesvědčit o tom, že prošlý náboj je nulový, neu­zavírá-li smyčka l vytvořená měrnou cívkou žádný proud. V opačném případě, kdy smyčka obepíná jistý proud I, je prošlý náboj úměrný tomuto proudu.

Praktický význam právě popsaného uspořádání spočívá v tom, že je možné za předpokladu platnosti Amp`erova zákona měřit proud ve vodičích podle jeho magnetických účinků, bez nutnosti zařazovat měřicí přístroj do příslušného ob­vodu. Výhody tohoto způsobu vyniknou zejména při měření velkých proudů, kdy by vlastní odpor měřicího přístroje mohl značně ovlivnit poměry v obvodu. Pro měření velkých střídavých proudů se komerčně zhotovují měrné cívky pev­ného tvaru, zpravidla na feromagnetickém jádru, které se nazývají měřicí trans­formátory.

b) Vlastní indukčnost přímých vodičů

Uvažujme nejdříve jediný nekonečně dlouhý velmi tenký vodič protékaný prou­dem I, vložený ve vakuu. Chceme-li určit vlastní indukčnost tohoto vodiče při­padající na délku d, můžeme postupovat tak, že zvolíme část radiální plochy šířky da a určíme celkový magnetický tok touto plochou (viz obr. 4.9a). Tok diferenciální ploškou dS bude dΨ  = Bd da a pro indukčnost dostaneme

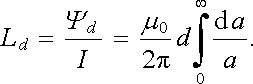Integrál však diverguje jak pro a ℜ →  0, tak pro a ℜ →  ℜ nekonecno , což ukazuje, že vyšetřo­vaný příklad je nepřípustně zidealizován. Divergenci pro a ℜ →  0 lze odstranit předpokladem konečného průměru vodiče. Pro a ℜ →  ℜ nekonecno však v případě jednoho nekonečného vodiče divergenci integrálu odstranit nelze, tudíž ani nelze najít konečnou hodnotu vlastní indukčnosti.

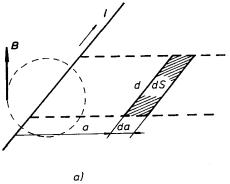
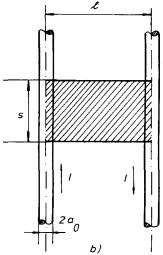
Obr. 4.9 K výpočtu indukčnosti přímých vodičů: a) jediný nekonečný vodič, b) dvojice přímých, rovnoběžných, nekonečně dlouhých vodičů.

Řešitelná je úloha o vlastní indukčnosti dvou přímých, rovnoběžných, neko­nečně dlouhých vodičů konečného průměru 2a₀, jejichž osy jsou vzdáleny o l a jimiž protéká proud I opačnými směry (viz obr. 4.9b). K určení celkového indukčního toku připadajícího na délku s vodičů stačí uvažovat část radiální plochy šířky s mezi osami obou vodičů. Předpokládejme nejdříve, že proud je rozdělen rovnoměrně po celém průřezu vodiče. Integraci magnetického toku je pak nutné rozdělit na dvě části; na část vně vodičů, kde je průběh magnetické indukce dán superpozicí příspěvků typu (3.86) , a na část uvnitř vodičů, kde prů­běh magnetického pole určuje vztah (3.87) . Za předpokladu, že vodiče mají re­lativní permeabilitu rovnou jedné a jsou umístěné ve vakuu, lze pro indukčnost L_s tedy psát

(4.25)

odkud po integraci dostaneme

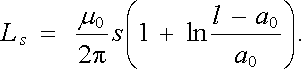(4.26)

Pro duté vodiče ovšem první člen v (4.25) i v (4.26) odpadne.

Zajímavé je srovnání výsledku pro duté vodiče s výsledkem příkladu 1.4.7f, ve kterém byla počítána kapacita dvojice válcových vodičů. Pro součin indukčnosti L₀ a kapacity C₀ připadající na jednotkovou délku platí

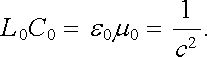(4.27)

c) Vlastní indukčnost kruhové smyčky

Máme určit vlastní indukčnost kruhové smyčky poloměru r vložené ve vakuu a protékané proudem I. Ze stejných důvodů jako v předchozím příkladu nemů­žeme smyčku považovat za nekonečně tenkou; budeme tedy předpokládat, že vodič má kruhový průřez o poloměru a₀.

K určení vlastní indukčnosti je třeba vypočítat magnetický tok kruhovou plochou ohraničenou osovou kružnicí smyčky. Přitom je třeba výpočet opět rozdělit na dvě části, tj. na tok uvnitř vodiče plochou ve tvaru mezikruží omezeného kružnicemi o poloměrech r a r - a₀ a na tok vně vodiče kruhovou plochou o polo­měru r - a₀.

Pro r >>  a₀ lze zanedbat zakřivení kružnice a vnitřní tok můžeme počítat jako v případě úseku přímého vodiče délky 2π r. Pokud jde o vnější část toku, pro jeho výpočet je nutná znalost průběhu magnetické indukce na celé kruhové ploše ohraničené smyčkou. Avšak jelikož vně smyčky můžeme proud I považovat za tekoucí nekonečně tenkou osovou kružnicí, je úloha ekvivalentní výpočtu vzá­jemné indukčnosti dvou tenkých koncentrických kruhových smyček o polo-měrech r a r - a₀ ležících v téže rovině. K tomu lze použít vzorec (4.21) . Vlastní výpočet integrálu není snadný. Položíme-li relativní permeabilitu vodiče rovnu jedné, vychází přibližný výsledek [6]

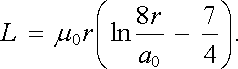(4.28)

d) Vlastní indukčnost solenoidu

Uvažujme dlouhý solenoid délky l a poloměru R, na němž je navinuto N_l závitů na jednotku délky. Zanedbáme-li okrajové efekty, můžeme magnetické pole uvnitř solenoidu považovat za homogenní s hodnotou magnetické indukce danou vztahem (3.95) . Celkový magnetický tok procházející všemi závity cívky Ψ je roven

,

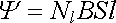kde S = π R² udává průřez solenoidu. Podle definice dostaneme pak pro vlastní indukčnost vztah

,

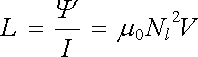(4.29a)

v němž V = Sl je objem solenoidu.

Přesnější výpočet zahrnující okrajové efekty (viz například [9]) dává

,

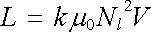(4.29b)

kde

.

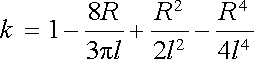e) Vlastní indukčnost toroidu

Toroidální cívky se uplatňují v celé řadě důležitých aplikací, nevyjímaje velká zařízení, jako je například tokamak, sloužící k udržení horkého plazmatu, nebo betatron (srov. 6.3.2d). Určíme vlastní indukčnost toroidu kruhového průřezu o poloměru b, na němž je navinuto celkem N závitů. Osová kružnice toroidu nechť má poloměr R₀ (viz obr. 4.10a).

Magnetické indukční čáry v toroidu jsou kružnice s osou v ose toroidu a veli­kost magnetické indukce ve vzdálenosti R od osy, která je je dána vztahem (3.96) , klesá s první mocninou R.

K určení vlastní indukčnosti musíme najít celkový magnetický tok Ψ uvnitř toroidu. Zvolíme kartézskou soustavu souřadnic s počátkem ve středu průřezu toroidu (obr. 4.10a), takže na povrchu průřezu platí x² + y² = b². Pro vlastní in­dukčnost pak máme

.

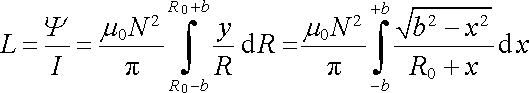Provedeme substituci x = bz a označíme R₀ = b C. Dostaneme

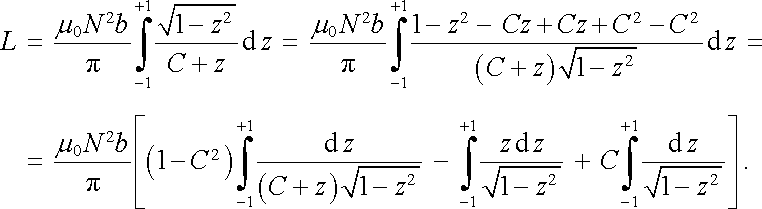První integrál v hranaté závorce řešíme substitucí 1/(C + z) = t, čímž dostaneme

,

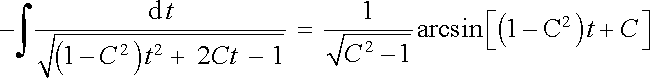druhý integrál je roven nule a třetí π . Celkově dostaneme tedy výsledek

.

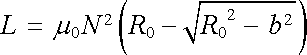(4.29c)

Pro tenký toroid, v přiblížení 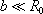, vychází

,

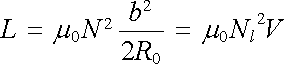(4.29d)

kde V = 2π ²R₀b² je objem toroidu a N_l počet závitů na jednotkové délce vinutí. Výsledek je tedy stejný jako u dlouhého solenoidu.

f) Vzájemná indukčnost dvou souosých smyček

Uvažujme vzájemnou indukčnost dvou souosých, stejně orientovaných smyček o poloměrech R₁, R₂, jejichž roviny leží ve vzdálenosti h (obr. 4.10b). Magnetická indukce vybuzená větší smyčkou ve středu smyčky menší je dána vzorcem

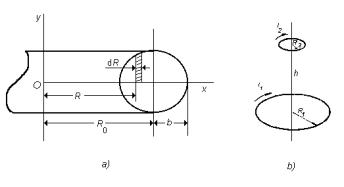
Obr. 4.10 K výpočtu a) vlastní indukčnosti toroidu, b) vzájemné indukčnosti dvojice souosých smyček.

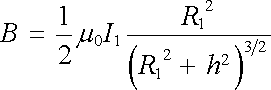a může být v průřezu této (menší) smyčky považována za homogenní. Pro hle­danou vzájemnou indukčnost pak ihned dostaneme

.

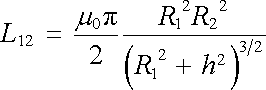(4.30a)

Speciálně pro koncentrické smyčky (h = 0) platí

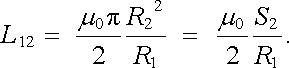(4.30b)

g) Vzájemná indukčnost dvojice souosých válcových cívek

Uvažme dvě válcové cívky o poloměrech R₁, R₂, počtech závitů N₁, N₂, a dél­kách l₁, l₂. Vypočtěme jejich vzájemnou indukčnost pro dva konkrétní případy:

1. Nechť obě cívky mají stejné rozměry, stejnou orientaci, jsou dostatečně dlouhé a jsou navinuty na společném jádru, takže magnetický tok jimi procháze­jící je totožný. Prochází-li cívkou (1) proud I₁, poteče jejím průřezem magne­tický tok Φ  = (₀I₁N₁S)/l . Celkové magnetické toky Ψ ₁, Ψ ₂₁ první a druhou cívkou budou tedy rovny

Odtud pro vlastní indukčnost a vzájemnou indukčnost obou cívek snadno dosta­neme výsledky

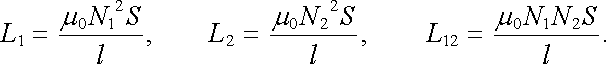(4.31)

Vidíme, že vzájemná indukčnost L₁₂ může také být vyjádřena ve tvaru

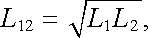(4.32)

což je nejvyšší mezní hodnota vzájemné indukčnosti dvou cívek a odpovídá situaci, kdy se obě cívky prostorově ztotožní a mají společný magnetický tok. (O různých stupních vazby dvou cívek bude jednáno ještě v čl. 4.2.3).

2. Nechť první cívka délky l₁ a poloměru R₁ je dostatečně dlouhá a druhá (krátká) cívka o poloměru R₂ <<  R₁ je do první cívky koaxiálně zasunuta. Obě cívky nechť mají souhlasnou orientaci. Pole vytvořené první cívkou můžeme v průřezu cívky druhé považovat za homogenní. Magnetický tok tekoucí průře­zem druhé cívky bude tedy roven (₀I₁N₁S)/l ₁ a pro vzájemnou indukčnost L₁₂ dostaneme

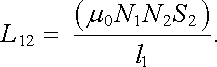(4.33)

---

---