Rovnicí (6,8) , respektive (6,9) jsme zavedli moment setrvačnosti jako charakteristiku rozložení hmotnosti tělesa která určuje průběh jeho otáčení kolem pevné osy. Po zavedení momentu setrvačnosti se nám podařilo přepsat větu (5,49) na tvar (6,13) . Rozšíříme nyní pojem momentu setrvačnosti tak, aby vystihoval vlastnosti tělesa při otáčení kolem pevného bodu. Zkusíme, zda je možno přepsat rovnici (5,49) na tvar (6,13) i pro otáčení tělesa kolem pevného bodu.
Počátek souřadnicové soustavy vložíme do bodu, kolem kterého se těleso reprezentované tuhou soustavou hmotných bodů otáčí. Potom dle (5,13) rychlost i-tého bodu soustavy
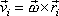 , , |
(6,28) |
kde
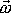 je okamžitá úhlová rychlost otáčení tělesa a
je okamžitá úhlová rychlost otáčení tělesa a
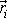 je polohový vektor i-tého bodu soustavy.
Dosadíme-li vyjádření rychlosti
(6,28)
do
(5,47)
, dostáváme pro celkový moment
hybnosti
je polohový vektor i-tého bodu soustavy.
Dosadíme-li vyjádření rychlosti
(6,28)
do
(5,47)
, dostáváme pro celkový moment
hybnosti
 soustavy vyjádření
soustavy vyjádření
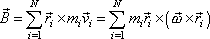 . . |
(6,29) |
Rovnici
(6,29)
rozepíšeme do složek, přičemž pořadové číslo i
jednotlivých hmotných
bodů budeme u jejich souřadnic psát nahoře. Vypočteme-li složky dvojitého
vektorového součinu
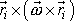 , dostáváme
, dostáváme
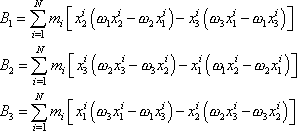 . . |
Po vytknutí složek vektoru úhlové rychlosti
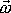 , který je společný pro celé těleso, můžeme poslední rovnici přepsat na tvar
, který je společný pro celé těleso, můžeme poslední rovnici přepsat na tvar
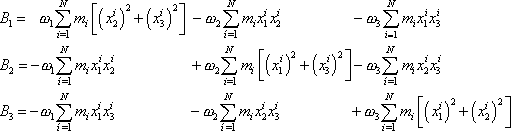 . . |
(6,30) |
Koeficienty u složek vektoru úhlové rychlosti mají rozměr shodný s rozměrem momentu setrvačnosti, označíme je
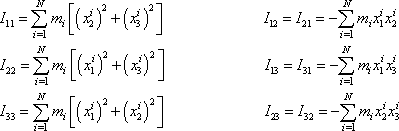 . . |
(6,31) |
Se zavedeným označením můžeme rovnice (6,30) přepsat na tvar
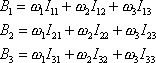 . . |
(6,31) |
Ve složkové symbolice zapíšeme rovnice (6,32) stručně jako
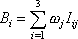 |
a užijeme-li sumačního (sčítacího) pravidla (viz dodatek D.1), můžeme celou soustavu (6,32) vystihnout jednoduchým zápisem
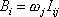 . . |
(6,33) |
Z rovnice
(6,12)
nebo z její stručné formy
(6,33)
plyne, že obecně nelze najít konstantu
 takovou, aby platilo
takovou, aby platilo
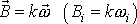 . Při otáčení tuhého tělesa kolem pevného bodu obecně není celkový moment
hybnosti tělesa
. Při otáčení tuhého tělesa kolem pevného bodu obecně není celkový moment
hybnosti tělesa
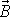 rovnoběžný s vektorem úhlové rychlosti otáčení
rovnoběžný s vektorem úhlové rychlosti otáčení
 .
.
Dosadíme-li za
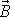 výraz
(6,33)
do rovnice
(5,49)
, dostáváme
výraz
(6,33)
do rovnice
(5,49)
, dostáváme
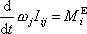 . . |
(6,34) |
Rovnice
(6,34)
formálně poněkud připomíná rovnici
(6,11)
.
Analogie však nemá hlubší smysl. Rovnice
(6,34)
platí v inerciální
souřadné soustavě. V té se však s časem mění souřadnice jednotlivých
bodů otáčejícího se tělesa a koeficienty
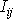 dané rovnicemi
(6,31)
obecně mění svou
velikost s časem. (Moment setrvačnosti vůči pevně dané ose užívaný
v předcházejícím článku závisí pouze na vzdálenostech bodů tělesa od osy,
což je neproměnná veličina nezávislá na volbě soustavy souřadné, a proto i
moment setrvačnosti je s časem konstantní.) Kromě toho výrazy
dané rovnicemi
(6,31)
obecně mění svou
velikost s časem. (Moment setrvačnosti vůči pevně dané ose užívaný
v předcházejícím článku závisí pouze na vzdálenostech bodů tělesa od osy,
což je neproměnná veličina nezávislá na volbě soustavy souřadné, a proto i
moment setrvačnosti je s časem konstantní.) Kromě toho výrazy
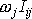 jsou součtem tří sčítanců. Rovnici
(6,34)
nelze upravit na tvar
(6,13)
, který má pohybová rovnice
(2,1)
hmotného bodu i
pohybová rovnice
(6,12)
pro otáčení tuhého tělesa kolem pevné osy a na který se
nám podařilo upravit větu
(5,33)
o hybnosti soustavy jejím převedením na tvar
(5,35)
. Rovnici tvaru
(6,13)
pro otáčení tuhého tělesa kolem bodu napsat nelze.
Rozbor pohybu se tím stává značně obtížný.
jsou součtem tří sčítanců. Rovnici
(6,34)
nelze upravit na tvar
(6,13)
, který má pohybová rovnice
(2,1)
hmotného bodu i
pohybová rovnice
(6,12)
pro otáčení tuhého tělesa kolem pevné osy a na který se
nám podařilo upravit větu
(5,33)
o hybnosti soustavy jejím převedením na tvar
(5,35)
. Rovnici tvaru
(6,13)
pro otáčení tuhého tělesa kolem bodu napsat nelze.
Rozbor pohybu se tím stává značně obtížný.
Rovnici
(6,29)
pro určení momentu hybnosti
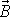 nemusíme chápat jen jako rovnici určující
nemusíme chápat jen jako rovnici určující
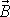 v inerciální soustavě souřadné nebo jak
budeme dále říkat pevné v prostoru, ale i jako výraz, kterým můžeme určit
vektor
v inerciální soustavě souřadné nebo jak
budeme dále říkat pevné v prostoru, ale i jako výraz, kterým můžeme určit
vektor
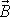 v soustavě souřadné spjaté
s otáčejícím se tělesem. Jedná se o prosté vyjádření vektoru
v soustavě souřadné spjaté
s otáčejícím se tělesem. Jedná se o prosté vyjádření vektoru
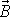 definovaného v inerciální soustavě
souřadné v jiné soustavě souřadné. Jinak by totiž, vzhledem k tomu,
že rychlosti jednotlivých bodů tělesa vůči soustavě pevně spjaté s tělesem
musí být nulové, moment hybnosti definovaný vůči soustavě souřadné spjaté
s tělesem neměl smysl. V soustavě souřadné spjaté s tělesem
označíme
definovaného v inerciální soustavě
souřadné v jiné soustavě souřadné. Jinak by totiž, vzhledem k tomu,
že rychlosti jednotlivých bodů tělesa vůči soustavě pevně spjaté s tělesem
musí být nulové, moment hybnosti definovaný vůči soustavě souřadné spjaté
s tělesem neměl smysl. V soustavě souřadné spjaté s tělesem
označíme
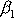 ,
,
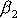 ,
,
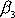 složky vektoru
složky vektoru
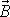 ,
,
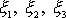 složky polohového vektoru
složky polohového vektoru
 a
a
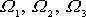 složky vektoru úhlové rychlosti
složky vektoru úhlové rychlosti
 . Nahradíme-li v rovnici
(6,30)
. Nahradíme-li v rovnici
(6,30)
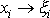 a
a
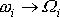 , dostaneme
, dostaneme
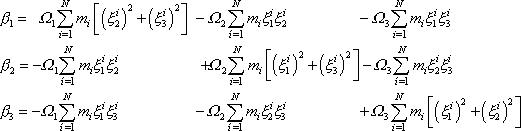 . . |
(6,35) |
Koeficienty u
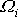 označíme nyní
označíme nyní
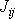 , tedy
, tedy
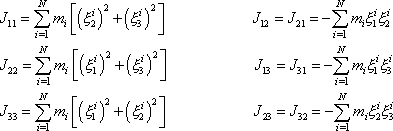 . . |
(6,36) |
Potom rovnice (6,35) můžeme stručně zapsat jako
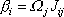 . . |
(6,37) |
V soustavě souřadné spjaté s tělesem (tuhou
soustavou hmotných bodů) jsou souřadnice
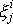
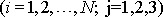 s časem stálé, a tedy i
koeficienty
s časem stálé, a tedy i
koeficienty
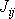 na rozdíl od koeficientů
na rozdíl od koeficientů
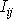 jsou s časem stálé neboli konstantní
veličiny. Koeficientům
jsou s časem stálé neboli konstantní
veličiny. Koeficientům
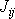 budeme říkat složky momentu setrvačnosti.
Výraz
budeme říkat složky momentu setrvačnosti.
Výraz
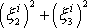 je roven čtverci vzdálenosti
je roven čtverci vzdálenosti
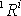 i-tého hmotného bodu od osy
i-tého hmotného bodu od osy
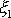 . Kdyby se těleso otáčelo kolem osy
. Kdyby se těleso otáčelo kolem osy
 , která by byla v tělese i v prostoru pevná, složka momentu
setrvačnosti
, která by byla v tělese i v prostoru pevná, složka momentu
setrvačnosti
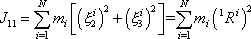 |
by byla rovna rovnicí
(6,8)
zavedenému momentu setrvačnosti.
Obdobný význam mají složky
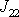 a
a
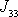 pro otáčení tělesa kolem druhé a třetí
souřadnicové osy pevně spjaté s tělesem. Složky se shodnými indexy
pro otáčení tělesa kolem druhé a třetí
souřadnicové osy pevně spjaté s tělesem. Složky se shodnými indexy
 budeme nazývat momenty setrvačnosti vůči souřadnicovým osám
a složky se smíšenými indexy
budeme nazývat momenty setrvačnosti vůči souřadnicovým osám
a složky se smíšenými indexy
 nazveme deviační momenty setrvačnosti.
nazveme deviační momenty setrvačnosti.
Převedeme rovnici
(5,49)
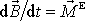 vyjadřující větu o momentu hybnosti
soustavy, tj. druhou větu impulsovou, do soustavy souřadné spjaté
s tělesem. Budeme předpokládat, že soustava souřadná pevná v tělese a
soustava souřadná pevná v prostoru mají společný počátek v bodě,
kolem kterého se těleso otáčí nebo v hmotném středu tělesa. Vektor
vyjadřující větu o momentu hybnosti
soustavy, tj. druhou větu impulsovou, do soustavy souřadné spjaté
s tělesem. Budeme předpokládat, že soustava souřadná pevná v tělese a
soustava souřadná pevná v prostoru mají společný počátek v bodě,
kolem kterého se těleso otáčí nebo v hmotném středu tělesa. Vektor
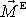 převedeme do soustavy souřadné spjaté s
tělesem jednoduše tak, že v této soustavě vyjádříme jeho složky; označíme
je
převedeme do soustavy souřadné spjaté s
tělesem jednoduše tak, že v této soustavě vyjádříme jeho složky; označíme
je
 . Chceme-li vyjádřit časovou změnu vektoru
. Chceme-li vyjádřit časovou změnu vektoru
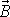 vůči soustavě souřadné spjaté
s tělesem
vůči soustavě souřadné spjaté
s tělesem
 , je vyjádření této derivace pomocí derivace
, je vyjádření této derivace pomocí derivace
 vektoru
vektoru
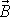 vůči soustavě souřadné pevné v prostoru
obtížnější. V následujícím odstavci si ukážeme na příkladu převodu vektoru
rychlosti mezi oběma soustavami, jak to lze udělat.
vůči soustavě souřadné pevné v prostoru
obtížnější. V následujícím odstavci si ukážeme na příkladu převodu vektoru
rychlosti mezi oběma soustavami, jak to lze udělat.
Polohový vektor
 určitého pevného bodu tělesa je v soustavě
souřadné spjaté s tělesem konstantní vektor. Polohový vektor téhož bodu
v prostoru se s časem mění. Rychlost bodu
určitého pevného bodu tělesa je v soustavě
souřadné spjaté s tělesem konstantní vektor. Polohový vektor téhož bodu
v prostoru se s časem mění. Rychlost bodu
 vůči soustavě souřadné spjaté s tělesem je nulová. Rychlost bodu
vůči soustavě souřadné spjaté s tělesem je nulová. Rychlost bodu
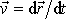 vůči soustavě souřadné pevné v prostoru je dána výrazem
(5,13)
vůči soustavě souřadné pevné v prostoru je dána výrazem
(5,13)
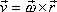 . . |
(5,13) |
Tedy derivace polohového vektoru
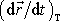 vůči soustavě souřadné spjaté s tělesem
a derivace téhož vektoru vůči soustavě souřadné pevné v prostoru
vůči soustavě souřadné spjaté s tělesem
a derivace téhož vektoru vůči soustavě souřadné pevné v prostoru
 se liší o výraz
se liší o výraz
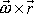 ;
;
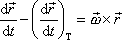 . . |
(6,38) |
U jiných vektorů, např. u vektoru
 , derivace vektoru vůči tělesu nemusí být nulová. Rozdíl
(6,38)
mezi derivací
vektoru
, derivace vektoru vůči tělesu nemusí být nulová. Rozdíl
(6,38)
mezi derivací
vektoru
 v prostoru a derivací
v prostoru a derivací
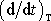 téhož vektoru vůči soustavě spjaté
s tělesem však zůstává. Mezi oběma derivacemi platí operátorový vztah (
téhož vektoru vůči soustavě spjaté
s tělesem však zůstává. Mezi oběma derivacemi platí operátorový vztah (
 , čl. 4 8,
, čl. 4 8,
 , čl. 229)
, čl. 229)
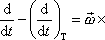 . . |
(6,39) |
Speciálně pro vektor celkové hybnosti tělesa
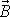 můžeme psát
můžeme psát
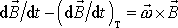 a po převedení derivace
a po převedení derivace
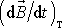 na druhou stranu rovnice máme
na druhou stranu rovnice máme
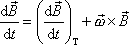 . . |
(6,40) |
Dosadíme-li vyjádření
(6,40)
do věty o momentu hybnosti soustavy
(5,49)
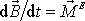 , dostáváme hledané vyjádření této věty v soustavě souřadné pevně spjaté
s tělesem
, dostáváme hledané vyjádření této věty v soustavě souřadné pevně spjaté
s tělesem
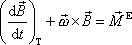 . . |
(6,41) |
Po rozepsání rovnice
(6,41)
do
složek, užijeme-li označení
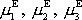 pro složky vektoru
pro složky vektoru
 v soustavě souřadné spjaté
s tělesem a pro složky ostatních vektorů stejného označení jako
v rovnici
(6,35)
, dostaneme
v soustavě souřadné spjaté
s tělesem a pro složky ostatních vektorů stejného označení jako
v rovnici
(6,35)
, dostaneme
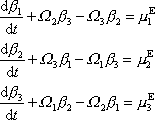 . . |
(6,42) |
Dosadíme-li do soustavy
(6,42)
vyjádření složek vektoru momentu hybnosti
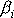 dle rovnice
(6,37)
dle rovnice
(6,37)
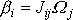 , kde
, kde
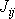 jsou složky momentu setrvačnosti vyjádřené
v soustavě souřadné spjaté s tělesem (
jsou složky momentu setrvačnosti vyjádřené
v soustavě souřadné spjaté s tělesem (
 jsou konstanty), přejde první z rovnic
(6,42)
na tvar
jsou konstanty), přejde první z rovnic
(6,42)
na tvar
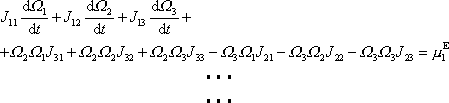 . . |
(6,43) |
Druhé dvě rovnice systému
(6,43)
, které lze získat
analogickým způsobem, nevypisujeme. Nahrazují je tečky. Rovnice
(6,43)
, které,
jak dále ukážeme, lze vhodnou volbou soustavy souřadné v tělese upravit na
jednodušší tvar, jsou pro stanovení pohybu tuhého tělesa otáčejícího se kolem
bodu vhodnější než formálně jednodušší rovnice
(6,34)
. V rovnicích
(6,43)
jsou totiž
 konstantní veličiny, jejichž hodnoty, při
dané volbě soustavy souřadné pevné v tělese, můžeme stanovit ještě před
řešením pohybové úlohy. Těchto šest čísel
konstantní veličiny, jejichž hodnoty, při
dané volbě soustavy souřadné pevné v tělese, můžeme stanovit ještě před
řešením pohybové úlohy. Těchto šest čísel
 ,
,
 ,
,
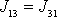 ,
,
 , které v rovnicích
(6,43)
charakterizují vlastnosti tělesa, spočítáme dle
definičních rovnic
(6,36)
.
, které v rovnicích
(6,43)
charakterizují vlastnosti tělesa, spočítáme dle
definičních rovnic
(6,36)
.
Při zadaných hodnotách
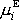 je soustava rovnic
(6,43)
soustavou tří
diferenciálních rovnic pro tři neznámé funkce
je soustava rovnic
(6,43)
soustavou tří
diferenciálních rovnic pro tři neznámé funkce
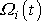 ; taková soustava je principiálně řešitelná. Soustava rovnic
(6,43)
nemá
jednoduchý tvar
(6,13)
, přesto však je hledanou úpravou rovnice
(5,49)
na
pohybovou rovnici tuhého tělesa, které se otáčí kolem pevného bodu. Rovnice
(6,43)
se nazývá Eulerova pohybová rovnice
a v této stati je uvedena ve své nejobecnější formě, jakou má
v libovolně volené soustavě souřadné. V souřadnicové soustavě, jejíž
osy jsou rovnoběžné s hlavními směry setrvačnosti, lze Eulerovu pohybovou
rovnici napsat v podstatně přehlednějším tvaru
(6,43´)
. Než tak učiníme,
musíme si vyložit, co jsou hlavní směry setrvačnosti.
; taková soustava je principiálně řešitelná. Soustava rovnic
(6,43)
nemá
jednoduchý tvar
(6,13)
, přesto však je hledanou úpravou rovnice
(5,49)
na
pohybovou rovnici tuhého tělesa, které se otáčí kolem pevného bodu. Rovnice
(6,43)
se nazývá Eulerova pohybová rovnice
a v této stati je uvedena ve své nejobecnější formě, jakou má
v libovolně volené soustavě souřadné. V souřadnicové soustavě, jejíž
osy jsou rovnoběžné s hlavními směry setrvačnosti, lze Eulerovu pohybovou
rovnici napsat v podstatně přehlednějším tvaru
(6,43´)
. Než tak učiníme,
musíme si vyložit, co jsou hlavní směry setrvačnosti.
Složky
(6,36)
 momentu setrvačnosti tvoří symetrický tenzor
2. řádu, pro který bývá užíván název tenzor momentu setrvačnosti.
momentu setrvačnosti tvoří symetrický tenzor
2. řádu, pro který bývá užíván název tenzor momentu setrvačnosti.
Pojem tenzoru vznikne rozšířením pojmu vektor; vektor je tenzor 1. řádu. Vektor lze jednoduše geometricky interpretovat jako orientovanou úsečku a z této interpretace snadno najdeme složky vektoru v libovolné soustavě souřadnic jako průměty úsečky do souřadnicových os. Změníme-li souřadnicovou soustavu, v které vyjadřujeme složky vektoru, změní se tedy jeho složky zcela určitým přesně definovaným způsobem. Stejně tak složky tenzoru při přechodu od jedné soustavy souřadné k druhé se mění (transformují) zcela určitým způsobem.
Geometrická interpretace tenzoru není již tak jednoduchá
jako u vektoru, protože počet jeho složek je větší, než je dimenze našeho
běžného prostoru. Někdy se pro symetrický tenzor druhého řádu, takový je i
tenzor momentu setrvačnosti, užívá znázornění elipsoidem. Šest nezávislých
složek symetrického tenzoru druhého řádu lze přiřadit šesti volitelným prvkům
elipsoidu, kterými jsou prostorová orientace os a velikosti tří vzájemně
kolmých poloos elipsoidu (viz např.
 ,
,
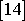 ). Odvodit způsob transformace složek tenzoru
druhého řádu z různých způsobů vyjádření elipsoidů v různých souřadnicových
soustavách není již tak jednoduché, jako je hledání průmětů orientované úsečky
do souřadnicových os, které postačí u tenzorů prvního řádu, tj. u vektorů.
Odvození transformačních rovnic tenzorů vyšších řádů v případě obecných
souřadnic potřebuje složitější matematický rozbor (viz např.
). Odvodit způsob transformace složek tenzoru
druhého řádu z různých způsobů vyjádření elipsoidů v různých souřadnicových
soustavách není již tak jednoduché, jako je hledání průmětů orientované úsečky
do souřadnicových os, které postačí u tenzorů prvního řádu, tj. u vektorů.
Odvození transformačních rovnic tenzorů vyšších řádů v případě obecných
souřadnic potřebuje složitější matematický rozbor (viz např.
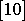 ,
,
 , kap. 8). V případě kartézských souřadnic, s kterými zde výhradně
budeme pracovat, je rozšíření formálně velmi jednoduché. Složky vektorů se
transformují stejně jako souřadnice (srov. vztah rovnic
(2,17)
a
(2,17´)
), mezi
složkami vektoru (tenzoru prvého řádu)
, kap. 8). V případě kartézských souřadnic, s kterými zde výhradně
budeme pracovat, je rozšíření formálně velmi jednoduché. Složky vektorů se
transformují stejně jako souřadnice (srov. vztah rovnic
(2,17)
a
(2,17´)
), mezi
složkami vektoru (tenzoru prvého řádu)
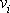 v čárkované a nečárkované souřadnicové soustavě platí vztah
v čárkované a nečárkované souřadnicové soustavě platí vztah
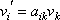 . . |
Tento vztah se pro případ tenzoru druhého řádu
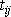 přirozeně rozšíří na tvar
přirozeně rozšíří na tvar
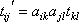 . . |
(6,44´) |
Čárkovaně jsou značeny složky tenzorů (vektoru a tenzoru
druhého řádu) v čárkované kartézské soustavě souřadnic, bez čárky složky
těchto tenzorů v nečárkované kartézské soustavě souřadnic,
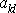 jsou koeficienty transformace (směrové
kosiny) popisující transformaci mezi čárkovanou a nečárkovanou souřadnicovou
soustavou.
jsou koeficienty transformace (směrové
kosiny) popisující transformaci mezi čárkovanou a nečárkovanou souřadnicovou
soustavou.
Podrobněji si význam transformačních rovnic (6,44´) ukážeme na příkladu momentu setrvačnosti, jehož složky se jakožto složky tenzoru
O platnosti transformačních rovnic (6,44) pro složky momentu setrvačnosti je možno se přesvědčit přímým dosazením souřadnic bodů tuhé soustavy hmotných bodů v čárkované a nečárkované soustavě do definičních rovnic složek (6,36) a zjištěním, zda získané složky rovnicím (6,44) vyhovují. Kladný výsledek potvrdí zde bez důkazu uvedené tvrzení, že složky momentu setrvačnosti tvoří tenzor druhého řádu.
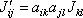 . . |
(6,44) |
 Máme-li v tuhém tělese dvě kartézské souřadnicové soustavy znázorněné na obr.63
(pro jednoduchost volíme společný počátek obou soustav), jsou složky
Máme-li v tuhém tělese dvě kartézské souřadnicové soustavy znázorněné na obr.63
(pro jednoduchost volíme společný počátek obou soustav), jsou složky
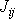 tenzoru momentu setrvačnosti
v nečár-kované soustavě a složky
tenzoru momentu setrvačnosti
v nečár-kované soustavě a složky
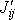 téhož ten-zoru v čárkované souřadnicové
soustavě vázány vztahy
(6,44)
. Koeficienty transformace
téhož ten-zoru v čárkované souřadnicové
soustavě vázány vztahy
(6,44)
. Koeficienty transformace
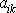 jsou složky (k je proměnný index)
jednotkového vektoru ležícího ve směru a smyslu i-té osy čárkované
soustavy souřadné vyjádřené v nečárkované soustavě souřadné, neboli
směrové kosiny i-té čárkované osy. Např.
jsou složky (k je proměnný index)
jednotkového vektoru ležícího ve směru a smyslu i-té osy čárkované
soustavy souřadné vyjádřené v nečárkované soustavě souřadné, neboli
směrové kosiny i-té čárkované osy. Např.
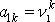 jsou složky v nečárkované soustavě
souřadné jednotkového vektoru ležícího v první čárkované ose (vektor
jsou složky v nečárkované soustavě
souřadné jednotkového vektoru ležícího v první čárkované ose (vektor
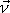 je na obr.63 vyznačen). V rovnici
(6,44)
jsou i, j
volitelné indexy a k, l sčítací indexy. Rovnice
(6,44)
reprezentuje tedy devět rovnic a na pravé straně každé rovnice je devět
sčítanců. Jelikož tenzor
je na obr.63 vyznačen). V rovnici
(6,44)
jsou i, j
volitelné indexy a k, l sčítací indexy. Rovnice
(6,44)
reprezentuje tedy devět rovnic a na pravé straně každé rovnice je devět
sčítanců. Jelikož tenzor
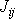 je symetrický, sníží se počet nezávislých
rovnic i sčítanců s různými koeficienty na šest.
je symetrický, sníží se počet nezávislých
rovnic i sčítanců s různými koeficienty na šest.
Známe-li tenzor momentu setrvačnosti
 a vektor úhlové rychlosti otáčení
a vektor úhlové rychlosti otáčení
 tělesa, můžeme dle rovnice
(6,37)
tělesa, můžeme dle rovnice
(6,37)
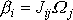 určit složky
určit složky
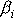 momentu celkové hybnosti tělesa
v soustavě souřadné spjaté s tělesem. Znalost vektoru
momentu celkové hybnosti tělesa
v soustavě souřadné spjaté s tělesem. Znalost vektoru
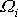 znamená, že známe směr osy otáčení
v tělese a rychlost rotace kolem ní. Předpokládejme, že osou rotace
proložíme třetí osu souřadnicové soustavy spjaté s tělesem. Pak
znamená, že známe směr osy otáčení
v tělese a rychlost rotace kolem ní. Předpokládejme, že osou rotace
proložíme třetí osu souřadnicové soustavy spjaté s tělesem. Pak
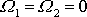 ,
,
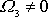 . Pro složku
. Pro složku
 momentu hybnosti dostáváme dle
(6,37)
obecné vyjádření
momentu hybnosti dostáváme dle
(6,37)
obecné vyjádření
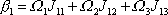 , , |
z kterého, je-li pouze
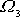 nenulové, plyne
nenulové, plyne
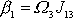 . Obdobně vypočítáme složky
. Obdobně vypočítáme složky
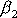 a
a
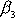 momentu hybnosti a dostaneme
momentu hybnosti a dostaneme
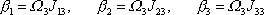 . . |
(6,45) |
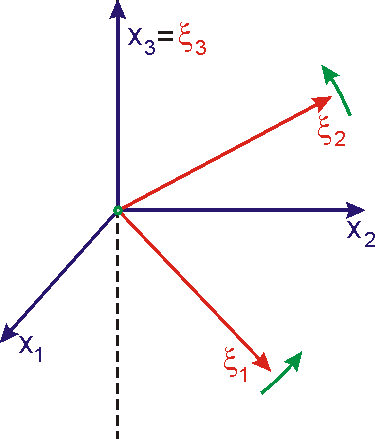 Jsou-li nenulové deviační složky tenzoru setrvačnosti
Jsou-li nenulové deviační složky tenzoru setrvačnosti
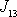 a
a
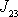 , má celkový moment hybnosti tělesa nejen složku
, má celkový moment hybnosti tělesa nejen složku
 do směru osy otáčení, ale i nenulové složky
do směru osy otáčení, ale i nenulové složky
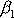 a
a
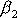 . Vektor
. Vektor
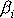 nemá tedy směr osy otáčení. V tomto
případě proložení třetí osy souřadnicové soustavy pevně spjaté s tělesem
osou otáčení lze učinit pouze v jednom okamžiku, v následujícím čase
se okamžitá osa otáčení z třetí souřadnicové soustavy odstěhuje.
nemá tedy směr osy otáčení. V tomto
případě proložení třetí osy souřadnicové soustavy pevně spjaté s tělesem
osou otáčení lze učinit pouze v jednom okamžiku, v následujícím čase
se okamžitá osa otáčení z třetí souřadnicové soustavy odstěhuje.
Je-li těleso upevněno na hřídeli nebo břitu, odpovídá
vyšetřovaný případ rotaci kolem pevné osy, která byla podrobně probírána
v minulém článku. Osou rotace o proložíme také osu
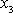 souřadnicové soustavy pevné v prostoru
(obr.64). To lze, neboť osa rotace je společnou přímkou obou soustav souřadnic.
Moment setrvačnosti J
definovaný rovnicí
(6,8)
je pak roven jak koeficientu
souřadnicové soustavy pevné v prostoru
(obr.64). To lze, neboť osa rotace je společnou přímkou obou soustav souřadnic.
Moment setrvačnosti J
definovaný rovnicí
(6,8)
je pak roven jak koeficientu
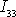 definovanému příslušnou rovnicí z
(6,31)
tak
složce
definovanému příslušnou rovnicí z
(6,31)
tak
složce
 tenzoru momentu setrvačnosti definované dle
(6,36)
;
tenzoru momentu setrvačnosti definované dle
(6,36)
;
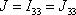 . . |
(6,46) |
Rovněž složky
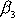 a
a
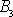 momentu hybnosti se sobě rovnají
momentu hybnosti se sobě rovnají
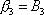 . . |
(6,47) |
Při rotaci kolem pevné osy jsou druhé dvě složky momentu hybnosti nulové v obou soustavách souřadných. Složky vypočtené rovnicemi (6,45) se sice snaží osu rotace v tělese změnit, ale upevnění hřídele (ložiska) či břit stěhování osy zabrání.
Vypočteme síly a momenty sil, kterými těleso roztočené kolem pevné osy působí na své uložení, tj. na ložiska nebo na břit. Roztočením tělesa přibudou k silám, které na uložení působí, i když těleso je v klidu (nejběžnější takovou silou je tíže tělesa), ještě odstředivá síla a momenty sil, které souvisí s výše zmíněnou snahou stěhovat osu rotace v tělese.
Odstředivá síla (soustava spojená s otáčející se
soustavou je neinerciální, a proto označení odstředivá síla je správné), působí
na hřídel (osu otáčení), když hmotný střed (těžiště) tělesa neleží na ose
otáčení. Její velikost je
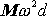 , kde M je hmotnost tělesa,
d vzdálenost těžiště od osy otáčení a w
úhlová rychlost otáčení. Má-li těleso
sloužit jako kolo, tzv. statickým vyvážením anulujeme vzdálenost d,
a tím i přídavnou odstředivou sílu působící na osu otáčení.
, kde M je hmotnost tělesa,
d vzdálenost těžiště od osy otáčení a w
úhlová rychlost otáčení. Má-li těleso
sloužit jako kolo, tzv. statickým vyvážením anulujeme vzdálenost d,
a tím i přídavnou odstředivou sílu působící na osu otáčení.
Pro výpočet momentů sil působících při roztočení na pevnou osu
otáčení procházející hmotným středem tělesa použijeme Eulerovu pohybovou
rovnici
(6,43)
. Její aplikace na uvažovaný případ rotace tuhého tělesa kolem
třetí osy (
 ,
,
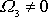 ) dává poměrně jednoduché rovnice
) dává poměrně jednoduché rovnice
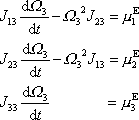 . . |
(6,48) |
Poslední rovnice soustavy
(6,48)
má stejný význam jako
rovnice
(6,12)
pro otáčení tuhého tělesa kolem pevné osy. Dle rovnice
(6,46)
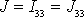 a jelikož třetí osy souřadnicové soustavy
pevné v prostoru a souřadnicové soustavy pevné v tělese splývají, je
také
a jelikož třetí osy souřadnicové soustavy
pevné v prostoru a souřadnicové soustavy pevné v tělese splývají, je
také
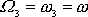 a
a
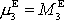 . Složka
. Složka
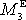 má pro rotaci kolem třetí osy význam momentu
má pro rotaci kolem třetí osy význam momentu
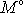 síly vůči ose.
síly vůči ose.
Rozborem prvních dvou rovnic soustavy
(6,48)
objasníme
význam deviačních momentů. Jsou-li deviační momenty
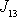 a
a
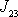 nenulové, je i při rovnoměrné rotaci tělesa,
tj. když
nenulové, je i při rovnoměrné rotaci tělesa,
tj. když
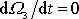 , nutno na těleso působit nenulovým momentem vnějších sil o složkách
, nutno na těleso působit nenulovým momentem vnějších sil o složkách
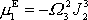 a
a
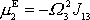 , aby se rotace kolem pevné osy udržela. Dle principu akce a reakce je potom
zřejmé, že těleso rotující kolem osy, vůči níž deviační momenty nejsou nulové,
působí na upevnění osy v prostoru nenulovým momentem síly o složkách
, aby se rotace kolem pevné osy udržela. Dle principu akce a reakce je potom
zřejmé, že těleso rotující kolem osy, vůči níž deviační momenty nejsou nulové,
působí na upevnění osy v prostoru nenulovým momentem síly o složkách
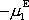 ,
,
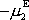 . Podrobný rozbor sil působících na ložiska, v kterých je osa rotujícího
tělesa upevněna, je podán např. v
. Podrobný rozbor sil působících na ložiska, v kterých je osa rotujícího
tělesa upevněna, je podán např. v
 , čl.220.
, čl.220.
V technických aplikacích soustav rotujících kolem pevné osy, např. u kol, se snažíme, aby při rotaci nepřistoupila k tíze tělesa žádná další síla působící na ložiska. Proto volíme za rotační takovou osu, na které leží těžiště soustavy a vůči které deviační momenty jsou nulové. Neprochází-li osa těžištěm soustavy, působí na ní při rotaci odstředivá síla. Nejsou-li deviační momenty vůči ose, kolem které se soustava otáčí, nulové, říkáme hantýrkou, že soustava (kolo) hází. I když soustavu navrhneme tak, aby obě výše uvedené podmínky byly splněny, konečné doladění jejich přesného splnění děláme experimentálně při tzv. vyvažování soustav. Již jsme uvedli, že doladění polohy těžiště se označuje jako statické vyvažování, doladění podmínky, aby deviační momenty vymizely, nazýváme dynamickým vyvažováním. Nejčastěji se setkáme s vyvažováním kol automobilu, které se má provést po každé výměně pneumatik. Vyvažují se však i složitější soustavy, např. turbosoustrojí elektráren.
Není-li osa rotace vazbami udržována v pevné poloze, nenulové hodnoty deviačních momentů v rovnici (6,48) způsobí, že osa rotace nebude mít vůči tělesu (a také v prostoru) stálou polohu. Osa začne tělesem putovat, a to i v případě, kdy výsledný moment vnějších sil je nulový. Tento případ podrobněji probereme v čl. 6.5.
Zodpovíme nyní otázku, zda jsou v tělese osy, vůči
kterým jsou deviační momenty nulové. V předchozí stati jsme si ukázali, že
pro takové osy je vektor momentu hybnosti
 rovnoběžný se směrem osy otáčení a tím též
s vektorem úhlové rychlosti
rovnoběžný se směrem osy otáčení a tím též
s vektorem úhlové rychlosti
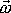 . Budeme tedy v tělese hledat osy, pro které, když jsou osami otáčení, je
moment hybnosti rovnoběžný s osou otáčení. Pak vektor momentu
hybnosti
. Budeme tedy v tělese hledat osy, pro které, když jsou osami otáčení, je
moment hybnosti rovnoběžný s osou otáčení. Pak vektor momentu
hybnosti
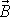 lze psát jako skalární násobek vektoru úhlové rychlosti otáčení
lze psát jako skalární násobek vektoru úhlové rychlosti otáčení
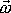 ,
,
 (
k
je konstanta), což v soustavě souřadné spjaté s tělesem zapíšeme ve
složkovém tvaru jako
(
k
je konstanta), což v soustavě souřadné spjaté s tělesem zapíšeme ve
složkovém tvaru jako
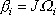 . . |
(6,49) |
V rovnici
(6,49)
jsme konstantu úměrnosti k označili J
, neboť má rozměr momentu setrvačnosti. Dosadíme-li požadovanou
vlastnost
(6,49)
vektoru
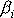 do obecné rovnice pro jeho vyjádření
(6,37)
, dostáváme
do obecné rovnice pro jeho vyjádření
(6,37)
, dostáváme
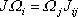 . . |
(6,50) |
Soustavu rovnic (6,50) rozepíšeme a všechny členy převedeme na levé strany rovnic, dostaneme
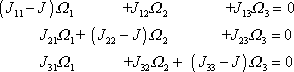 . . |
(6,51) |
Rovnice
(6,51)
tvoří homogenní soustavu lineárních
algebraických rovnic pro neznámé složky
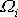 vektoru úhlové rychlosti otáčení. Aby soustava
rovnic
(6,51)
měla netriviální řešení, tj. takové řešení, kdy alespoň jedna ze
složek
vektoru úhlové rychlosti otáčení. Aby soustava
rovnic
(6,51)
měla netriviální řešení, tj. takové řešení, kdy alespoň jedna ze
složek
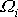 je různá od nuly, je nutné a stačí, aby
determinant soustavy byl roven nule (viz např.
je různá od nuly, je nutné a stačí, aby
determinant soustavy byl roven nule (viz např.
 , kap.1,
, kap.1,
 , kap.1). Tedy
, kap.1). Tedy
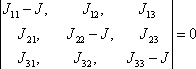 . . |
(6,52) |
Rozepíšeme-li determinant
(6,52)
, získáme kubickou rovnici
pro neznámou konstantu J. Bez důkazu uvedeme, že pro reálné hodnoty
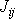 má rovnice
(6,52)
všechny tři kořeny reálné,
a tedy pro tři hodnoty konstant
má rovnice
(6,52)
všechny tři kořeny reálné,
a tedy pro tři hodnoty konstant
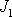 ,
,
 ,
,
 lze splnit rovnici
(6,52)
. Každé z konstant
lze splnit rovnici
(6,52)
. Každé z konstant
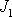 ,
,
 ,
,
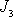 odpovídá jedno řešení rovnice
(6,51)
, tedy
jedna trojice složek
odpovídá jedno řešení rovnice
(6,51)
, tedy
jedna trojice složek
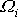 vektoru úhlové rychlosti otáčení. Rovnicemi
(6,51)
jsou však vektory
vektoru úhlové rychlosti otáčení. Rovnicemi
(6,51)
jsou však vektory
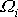 určeny až na libovolnou konstantu, jak se
lze přesvědčit přímým dosazením do soustavy rovnic
(6,51)
. (Je-li
určeny až na libovolnou konstantu, jak se
lze přesvědčit přímým dosazením do soustavy rovnic
(6,51)
. (Je-li
 jejich řešením, je řešením také
jejich řešením, je řešením také
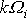 , neboť po dosazení do rovnic
(6,51)
lze konstantu k
ve všech rovnicích soustavy zkrátit.) Jako
charakteristické vektory řešení rovnic
(6,51)
vybereme jednotkové vektory
, neboť po dosazení do rovnic
(6,51)
lze konstantu k
ve všech rovnicích soustavy zkrátit.) Jako
charakteristické vektory řešení rovnic
(6,51)
vybereme jednotkové vektory
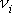 ve směru vektorů
ve směru vektorů
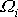 . Vektory
. Vektory
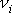 jsou jednotkovými vektory ve směru hledaných
os otáčení. Lze ukázat, že jsou-li všechny konstanty
jsou jednotkovými vektory ve směru hledaných
os otáčení. Lze ukázat, že jsou-li všechny konstanty
 ,
,
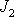 ,
,
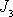 od sebe různé, jsou jim odpovídající vektory
od sebe různé, jsou jim odpovídající vektory
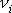 vzájemně kolmé. Podmínku
(6,49)
, aby vektory
vzájemně kolmé. Podmínku
(6,49)
, aby vektory
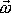 a
a
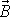 byly rovnoběžné, lze tedy splnit alespoň pro jednu trojici vzájemně kolmých vektorů.
byly rovnoběžné, lze tedy splnit alespoň pro jednu trojici vzájemně kolmých vektorů.
V libovolném tělese existují pro každý bod nejméně tři tímto bodem procházející osy takové, že při rotaci kolem nich celkový moment hybnosti tělesa je rovnoběžný se směrem osy otáčení.
Těmito osami můžeme proložit osy
kartézské souřadnicové soustavy s počátkem v uvažovaném bodě.
Uvažujme, že těleso rotuje kolem jedné z os takto zvolené souřadnicové
soustavy. Budeme ji pokládat za třetí osu. Jelikož moment hybnosti
v uvažované soustavě musí být rovnoběžný s osou otáčení, tedy
s třetí osou, jsou první a druhá složka momentu hybnosti nulové,
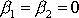 . Z prvých dvou rovnic
(6,45)
potom plyne, že ve zvolené soustavě souřadnic
musí být
. Z prvých dvou rovnic
(6,45)
potom plyne, že ve zvolené soustavě souřadnic
musí být
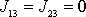 . Napíšeme-li rovnice typu
(6,45)
pro rotaci kolem druhých dvou souřadnicových os
a uvědomíme-li si, že při rotaci kolem kterékoli osy uvažované kartézské
soustavy souřadnic má moment hybnosti směr osy, dostaneme podmínku
. Napíšeme-li rovnice typu
(6,45)
pro rotaci kolem druhých dvou souřadnicových os
a uvědomíme-li si, že při rotaci kolem kterékoli osy uvažované kartézské
soustavy souřadnic má moment hybnosti směr osy, dostaneme podmínku
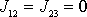 rozborem rotace kolem osy
rozborem rotace kolem osy
 a podmínku
a podmínku
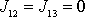 rozborem rotace kolem osy
rozborem rotace kolem osy
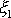 .
.
Proložíme-li osy kartézské souřadnicové soustavy těmi směry,
ve kterých při rotaci moment hybnosti má směr os otáčení, deviační momenty
vymizí. V takové souřadnicové soustavě jsou nenulové pouze složky
 ,
,
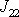 a
a
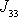 tenzoru momentu setrvačnosti a jeho složky se smíšenými indexy
tenzoru momentu setrvačnosti a jeho složky se smíšenými indexy
 ,
,
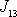 ,
,
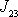 vymizí. Momenty setrvačnosti vůči osám jsou rovny kořenům rovnice
(6,52)
,
vymizí. Momenty setrvačnosti vůči osám jsou rovny kořenům rovnice
(6,52)
,
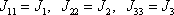 |
(6,53) |
a deviační momenty jsou nulové,
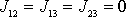 .
.
Osám, vůči nimž smíšené (deviační)
složky tenzoru setrvačnosti vymizí, říkáme hlavní osy
tenzoru momentu setrvačnosti a momentům setrvačnosti
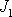 ,
,
 ,
,
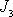 vůči těmto osám říkáme hlavní momenty setrvačnosti.
vůči těmto osám říkáme hlavní momenty setrvačnosti.
Šest údajů popisujících tenzor momentu setrvačnosti se
v případě jeho popisu v souřadnicové soustavě proložené hlavními
osami setrvačnosti (hlavní souřadnicové soustavě) skládá z tří údajů udávajících
polohu této soustavy v tělese a tří hodnot hlavních momentů setrvačnosti,
pro které se v této souřadnicové soustavě užívá jednosložkové
označení
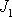 ,
,
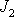 ,
,
 . Je-li těleso homogenní a má-li nějaké osy symetrie, jsou tyto osy symetrie
hlavními osami setrvačnosti.
. Je-li těleso homogenní a má-li nějaké osy symetrie, jsou tyto osy symetrie
hlavními osami setrvačnosti.
Naznačili jsme, jak lze řešit rovnici
(6,50)
. Řešením rovnic
tohoto typu, které se označují jako sekulární rovnice, určíme hlavní osy
libovolného symetrického tenzoru druhého řádu. V naznačeném postupu nebylo
nikde podstatné, že
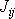 je tenzorem momentu setrvačnosti. Řešení sekulární rovnice je popsáno např. v
je tenzorem momentu setrvačnosti. Řešení sekulární rovnice je popsáno např. v
 ,
,
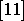 , kde jsou objasněna ta tvrzení, která zde byla uvedena bez důkazů. Pro rovinný
problém, kdy tenzor druhého řádu má jen čtyři složky (2x2), předvedeme řešení
sekulární rovnice na příkladu hledání hlavních směrů tenzoru napětí
popisujícího smyk (II, čl.1.4). Ukážeme, že smykové napětí lze vyjádřit
v hlavní soustavě souřadnic, která je proti původní otočena o 45o,
jako tah v rovině kolmé
na osu původně pravého úhlu vzorku tvaru kvádru, který se deformací zmenší, a
tlak v rovině na ní kolmé.
, kde jsou objasněna ta tvrzení, která zde byla uvedena bez důkazů. Pro rovinný
problém, kdy tenzor druhého řádu má jen čtyři složky (2x2), předvedeme řešení
sekulární rovnice na příkladu hledání hlavních směrů tenzoru napětí
popisujícího smyk (II, čl.1.4). Ukážeme, že smykové napětí lze vyjádřit
v hlavní soustavě souřadnic, která je proti původní otočena o 45o,
jako tah v rovině kolmé
na osu původně pravého úhlu vzorku tvaru kvádru, který se deformací zmenší, a
tlak v rovině na ní kolmé.
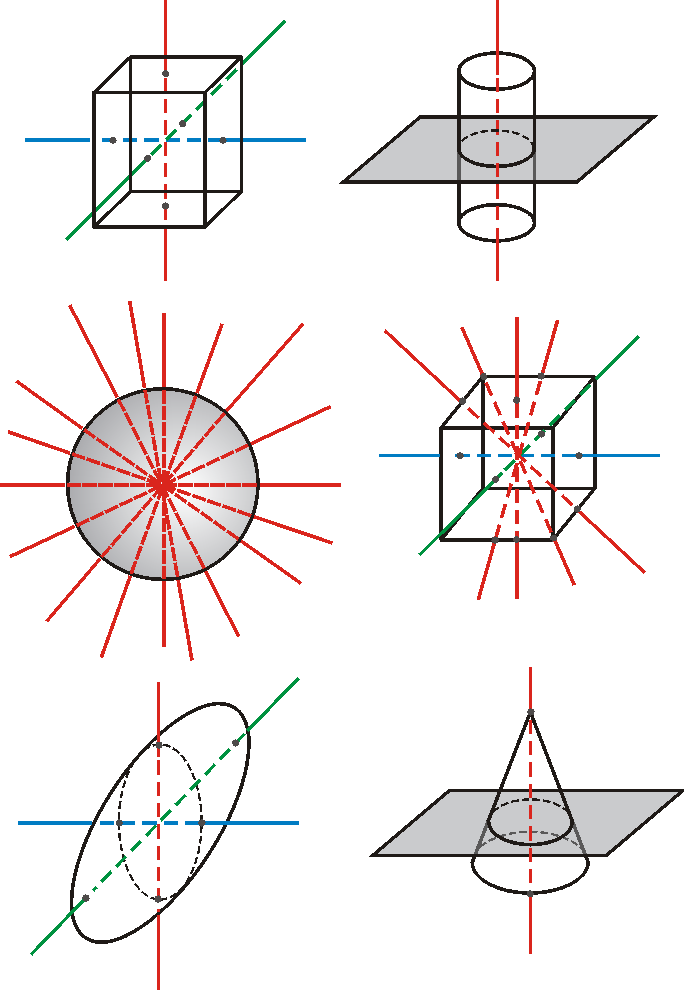 Směry hlavních os tenzoru momentu setrvačnosti pro homogenní
tělesa jednoduchých geometrických tvarů procházející jejich těžištěm jsou
vyznačeny na obr.65. Jelikož v rotačně
symetrickém tělese všechny osy kolmé k ose symetrie a různoběžné
s ní jsou identické, momenty setrvačnosti vůči nim jsou stejné a všechny
tyto osy jsou hlavními osami setrvačnosti. U homogenní koule všechny osy
procházející jejím hmotným středem jsou hlavními osami setrvačnosti. Totéž
platí i pro homogenní krychli. Symetrie homogenních těles umožní i
v dalších případech najít směr hlavních os setrvačnosti bez obtížného
řešení sekulární rovnice.
Směry hlavních os tenzoru momentu setrvačnosti pro homogenní
tělesa jednoduchých geometrických tvarů procházející jejich těžištěm jsou
vyznačeny na obr.65. Jelikož v rotačně
symetrickém tělese všechny osy kolmé k ose symetrie a různoběžné
s ní jsou identické, momenty setrvačnosti vůči nim jsou stejné a všechny
tyto osy jsou hlavními osami setrvačnosti. U homogenní koule všechny osy
procházející jejím hmotným středem jsou hlavními osami setrvačnosti. Totéž
platí i pro homogenní krychli. Symetrie homogenních těles umožní i
v dalších případech najít směr hlavních os setrvačnosti bez obtížného
řešení sekulární rovnice.
Zvolíme-li souřadnicovou soustavu pevnou v tělese ve směru hlavních os tenzoru momentu setrvačnosti, tedy hlavní souřadnicovou soustavu, deviační momenty jsou nulové a rovnice (6,43) , která vyjadřuje Eulerovu pohybovou rovnici v obecné souřadnicové soustavě spjaté s tělesem, se zjednoduší na tvar
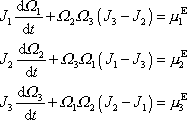 . . |
(6,43´) |
V rovnicích
(6,43´)
jsme momenty setrvačnosti
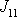 ,
,
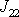 ,
,
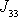 označili dle
(6,53)
jako
označili dle
(6,53)
jako
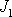 ,
,
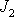 ,
,
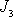 .
.
Rovnice (6,43´) udávají vyjádření věty (5,49) o momentu hybnosti soustavy v soustavě souřadnic zvolené v tělese tak, že osy souřadnic splývají se směry hlavních os tenzoru momentu setrvačnosti. Název Eulerovy pohybové rovnice (Eulerova pohybová rovnice) se někdy omezuje jen na rovnice napsané v přehledném tvaru (6,43´) .
Ukážeme, jak lze určit moment setrvačnosti J
vůči libovolné ose procházející bodem,
známe-li pro tento bod tenzor momentu setrvačnosti. Momentem setrvačnosti J
vůči ose rozumíme skalární veličinu definovanou
rovnicí
(6,8)
. Znalost tenzoru momentu setrvačnosti znamená, že známe hodnoty
jeho složek
 . Odvodíme vztah, který nám umožní stanovit hodnotu momentu setrvačnosti J
pro libovolnou osu procházející daným bodem,
známe-li směr této osy; ten určíme jednotkovým vektorem
. Odvodíme vztah, který nám umožní stanovit hodnotu momentu setrvačnosti J
pro libovolnou osu procházející daným bodem,
známe-li směr této osy; ten určíme jednotkovým vektorem
 mířícím ve směru osy.
mířícím ve směru osy.
Vyjdeme z rovnice pro otáčení tělesa kolem pevné osy, která byla podrobně rozebraná v minulém článku. Tuto rovnici lze získat z rovnice (5,49)
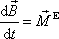 , , |
vyjadřující druhou větu impulsovou. Tuto rovnici promítneme
do směru osy, tj. skalárně ji vynásobíme jednotkovým vektorem
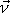 ve směru osy otáčení. Dostaneme
ve směru osy otáčení. Dostaneme
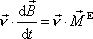 . . |
Jelikož
 je konstantní vektor
je konstantní vektor
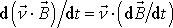 a dle
(6,14)
a dle
(6,14)
 , můžeme dále psát
, můžeme dále psát
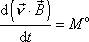 . . |
(6,54) |
Porovnáme-li rovnici (6,54) s rovnicí (6,11) , dostaneme
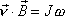 . . |
(6,55) |
Průmět vektoru celkového momentu hybnosti
 do osy otáčení je roven součinu momentu
setrvačnosti J a úhlové rychlosti
otáčení tělesa
do osy otáčení je roven součinu momentu
setrvačnosti J a úhlové rychlosti
otáčení tělesa
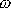 . Průmět momentu hybnosti do osy otáčení je stejná veličina, ať průmět popisujeme
v soustavě souřadné pevné v prostoru, v níž jsme provedli
předcházející úvahu, nebo v soustavě souřadné pevné v tělese. Platí
tedy též
. Průmět momentu hybnosti do osy otáčení je stejná veličina, ať průmět popisujeme
v soustavě souřadné pevné v prostoru, v níž jsme provedli
předcházející úvahu, nebo v soustavě souřadné pevné v tělese. Platí
tedy též
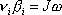 , , |
(6,56) |
kde
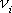 jsou nyní složky jednotkového vektoru ve
směru osy otáčení v soustavě souřadnic spjaté s tělesem. Do rovnice
(6,56)
dosadíme vyjádření
jsou nyní složky jednotkového vektoru ve
směru osy otáčení v soustavě souřadnic spjaté s tělesem. Do rovnice
(6,56)
dosadíme vyjádření
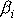 dle
(6,37)
, dostáváme
dle
(6,37)
, dostáváme
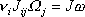 . . |
(6,57) |
Při otáčení kolem pevné osy má vektor
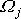 směr této osy, tedy
směr této osy, tedy
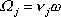 , , |
(6,58) |
kde
 je stejně jako na pravé straně rovnice
(6,57)
úhlová rychlost rotace (vektor v přímce, ne velikost vektoru).
Dosadíme-li
je stejně jako na pravé straně rovnice
(6,57)
úhlová rychlost rotace (vektor v přímce, ne velikost vektoru).
Dosadíme-li
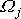 vyjádřené dle
(6,58)
do rovnice
(6,57)
,
dostaneme po přeskupení součinitelů na levé straně rovnice
vyjádřené dle
(6,58)
do rovnice
(6,57)
,
dostaneme po přeskupení součinitelů na levé straně rovnice
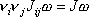 . . |
(6,59) |
Po zkrácení nenulové hodnoty
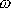 v rovnici
(6,59)
dostáváme hledané
vyjádření momentu setrvačnosti J
dle složek tenzoru momentu setrvačnosti
v rovnici
(6,59)
dostáváme hledané
vyjádření momentu setrvačnosti J
dle složek tenzoru momentu setrvačnosti
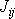 :
:
Dle rovnice
(6,60)
můžeme určit moment setrvačnosti J
tělesa vůči libovolné ose o
procházející bodem, pro který známe tensor momentu setrvačnosti. Na
obr.66 je uvažovaný bod označen A a je do něj položen počátek soustavy
souřadnic, v které vyjádříme složky tensoru setrvačnosti
 (obr.66 a)). Směr osy o
je určen jednotkovým vektorem
(obr.66 a)). Směr osy o
je určen jednotkovým vektorem
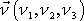 . Rozepsáním rovnice
(6,60)
dostaneme pro J vyjádření
. Rozepsáním rovnice
(6,60)
dostaneme pro J vyjádření
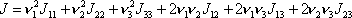 . . |
(6,60´) |
V rovnici
(6,60´)
jsme užili symetrie tensoru, tj.
vztahů
 a pořadí sčítanců jsme oproti sledu
naznačenému rovnicí
(6,60)
zpřeházeli.
a pořadí sčítanců jsme oproti sledu
naznačenému rovnicí
(6,60)
zpřeházeli.
Jak jsme ukázali ve stati 6.2.5, existuje pro bod A
v tělese taková kartézská soustava souřadnic, v které deviační
momenty (složky tenzoru
 se smíšenými indexy) jsou nulové. Je to
souřadnicová soustava, jejíž osy mají směr hlavních os setrvačnosti. Tato
soustava je znázorněná na obr.66 b).
Symboly os této význačné souřadnicové soustavy jsou označeny pruhem nad
označením osy.
se smíšenými indexy) jsou nulové. Je to
souřadnicová soustava, jejíž osy mají směr hlavních os setrvačnosti. Tato
soustava je znázorněná na obr.66 b).
Symboly os této význačné souřadnicové soustavy jsou označeny pruhem nad
označením osy.
Vyjádření momentu setrvačnosti J v pruhované soustavě, tj. v souřadnicové soustavě proložené hlavními osami setrvačnosti, je dáno výrazem
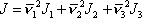 , , |
(6,60´´) |
 který pro tuto speciální souřadnicovou soustavu plyne z obecného vzorce
(6,60)
.
V rovnici
(6,60´´)
jsme užili pro momenty setrvačnosti vůči osám
zkráceného označení
který pro tuto speciální souřadnicovou soustavu plyne z obecného vzorce
(6,60)
.
V rovnici
(6,60´´)
jsme užili pro momenty setrvačnosti vůči osám
zkráceného označení
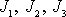 místo
místo
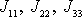 a složky jednotkového vektoru
a složky jednotkového vektoru
 v pruhované souřadnicové soustavě jsme označili
v pruhované souřadnicové soustavě jsme označili
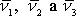 .
.