V předcházející stati jsme ukázali, že znalost tenzoru setrvačnosti v daném bodě znamená možnost stanovení momentu setrvačnosti vůči libovolné ose procházející daným bodem. V tuhém tělese taková znalost dokonce znamená možnost stanovit moment setrvačnosti vůči libovolné ose procházející tělesem, známe-li jeho celkovou hmotnost a polohu jeho hmotného středu. Momenty setrvačnosti vůči rovnoběžným osám jsou totiž vázány jednoduchým vztahem, který se nazývá Steinerova věta. Uvedeme její znění:
Moment setrvačnosti J
tělesa vůči libovolné ose o
je roven součtu momentu setrvačnosti
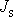 vůči ose
vůči ose
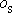 procházející hmotným středem tělesa
rovnoběžně s osou o
a součinu hmotnosti tělesa M
se čtvercem vzdálenosti d obou os;
procházející hmotným středem tělesa
rovnoběžně s osou o
a součinu hmotnosti tělesa M
se čtvercem vzdálenosti d obou os;
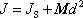 . . |
(6,61) |
Z věty bezprostředně plyne, že znalost tenzoru momentu setrvačnosti v hmotném středu (těžišti) tělesa umožní spočítat moment setrvačnosti tělesa vůči libovolné ose. Nejprve dle vzorce (6,60) spočítáme moment setrvačnosti vůči ose procházející hmotným středem tělesa rovnoběžně s osou, vůči které chceme moment setrvačnosti spočítat, a potom dle Steinerovy věty spočítáme hledaný moment setrvačnosti. Vztah mezi momenty setrvačnosti vůči libovolným rovnoběžným osám najdeme porovnáním čtverců jejich vzdáleností od hmotného středu. Ze Steinerovy věty vyplývá, že směry hlavních os setrvačnosti jsou ve všech bodech tuhého tělesa stejné.
 Nyní dokážeme platnost
Steinerovy věty. Zvolíme kartézskou soustavu souřadnic s počátkem
v hmotném středu S soustavy a třetí osou ve směru
Nyní dokážeme platnost
Steinerovy věty. Zvolíme kartézskou soustavu souřadnic s počátkem
v hmotném středu S soustavy a třetí osou ve směru
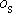 . První souřadnico-vou osu zvolíme tak, aby protínala osu o.
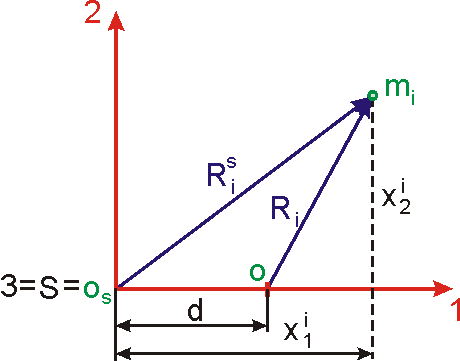
Pohled ve směru a proti smyslu třetí souřadnicové osy je na obr.67.
V obrázku je znázorněn i-tý bod
. První souřadnico-vou osu zvolíme tak, aby protínala osu o.
Pohled ve směru a proti smyslu třetí souřadnicové osy je na obr.67.
V obrázku je znázorněn i-tý bod
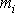 tuhé soustavy hmot-ných bodů, která
reprezentuje těleso. Jsou znázorněny souřadnice
tuhé soustavy hmot-ných bodů, která
reprezentuje těleso. Jsou znázorněny souřadnice
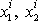 bodu
bodu
 , vzdálenost
, vzdálenost
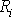 bodu
bodu
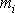 od osy o a vzdálenost
od osy o a vzdálenost
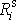 bodu
bodu
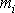 od osy
od osy
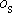 . Zřejmě platí
. Zřejmě platí
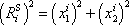 |
(6,62) |
a
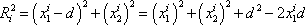 . . |
(6,63) |
Dle definiční rovnice
(6,8)
moment setrvačnosti J
tělesa vůči ose o je dán výrazem
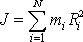 . Dosadíme-li do tohoto vyjádření za
. Dosadíme-li do tohoto vyjádření za
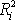 dle
(6,63)
, dostáváme
dle
(6,63)
, dostáváme
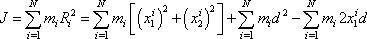 . . |
(6,64) |
První člen na pravé straně rovnice
(6,64)
lze
s přihlédnutím k rovnici
(6,62)
psát jako
 a je to tedy moment setrvačnosti
a je to tedy moment setrvačnosti
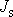 tělesa vůči ose
tělesa vůči ose
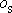 ;
;
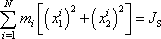 . . |
(6,65) |
V druhém členu na pravé straně rovnice
(6,64)
je
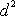 konstantní veličina a můžeme ji ze součtu vytknout,
konstantní veličina a můžeme ji ze součtu vytknout,
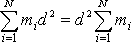 . Jelikož
. Jelikož
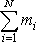 je celková hmotnost tělesa M, lze psát
je celková hmotnost tělesa M, lze psát
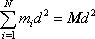 . . |
(6,66) |
Třetí člen na pravé straně rovnice
(6,64)
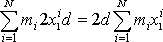 . Výraz
. Výraz
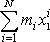 je dle
(5,7´)
roven první souřadnici
je dle
(5,7´)
roven první souřadnici
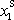 hmotného středu tělesa násobené hmotností M tělesa.
hmotného středu tělesa násobené hmotností M tělesa.
Počátek soustavy souřadnic, v které je prováděn
výpočet, je však zvolen v hmotném středu tělesa, a proto všechny
souřadnice hmotného středu jsou nulové, speciálně
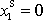 . Tedy
. Tedy
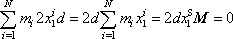 . . |
(6,67) |
Užijeme-li rovnice (6,65) , (6,66) a (6,67) , můžeme moment setrvačnosti J daný rovnicí (6,64) zapsat jako
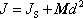 , , |
což je znění Steinerovy věty (6,61) , a tedy důkaz její platnosti je proveden..
Známe-li tensor momentu setrvačnosti pro hmotný střed
tělesa, můžeme dle rovnice
(6,60)
určit moment setrvačnosti vůči libovolné ose
procházející hmotným středem tělesa. Dle Steinerovy věty můžeme pak najít
moment setrvačnosti vůči libovolné ose procházející tělesem. K určení
momentu setrvačnosti tělesa vůči libovolné ose stačí znát šest konstant, šest
složek symetrického tensoru
 momentu setrvačnosti pro hmotný střed
tělesa. Znalost šesti složek tensoru momentu setrvačnosti lze též nahradit
znalostí hlavních momentů setrvačnosti
momentu setrvačnosti pro hmotný střed
tělesa. Znalost šesti složek tensoru momentu setrvačnosti lze též nahradit
znalostí hlavních momentů setrvačnosti
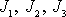 a směrů hlavních os pro hmotný střed.
K určení směru hlavních os je třeba tří údajů a spolu
s hodnotami
a směrů hlavních os pro hmotný střed.
K určení směru hlavních os je třeba tří údajů a spolu
s hodnotami
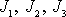 máme tak znovu šest konstant pro určení
momentu setrvačnosti tělesa vůči libovolné ose.
máme tak znovu šest konstant pro určení
momentu setrvačnosti tělesa vůči libovolné ose.
V článku 5.5 jsme odvodili Königovu větu
(5,74)
, dle
níž kinetickou energii
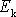 soustavy hmotných bodů lze rozložit na
člen
soustavy hmotných bodů lze rozložit na
člen
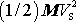 odpovídající pohybu hmotného středu soustavy
a na vnitřní kinetickou energii soustavy
odpovídající pohybu hmotného středu soustavy
a na vnitřní kinetickou energii soustavy
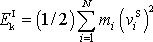 . Pro tuhou soustavu hmotných bodů a tuhé těleso lze rychlost
. Pro tuhou soustavu hmotných bodů a tuhé těleso lze rychlost
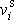 i-tého
bodu vůči hmotnému středu psát dle
(5,69)
jako
i-tého
bodu vůči hmotnému středu psát dle
(5,69)
jako
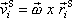 , , |
(5,69) |
kde
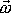 je okamžitý vektor úhlové rychlosti otáčení tělesa a
je okamžitý vektor úhlové rychlosti otáčení tělesa a
 vektor určující polohu i-tého
bodu vůči hmotnému středu tělesa. Dle
(5,21)
úhlová rychlost otáčení nezávisí
na bodu, vůči kterému ji uvažujeme, a proto otáčení tělesa určené vektorem
vektor určující polohu i-tého
bodu vůči hmotnému středu tělesa. Dle
(5,21)
úhlová rychlost otáčení nezávisí
na bodu, vůči kterému ji uvažujeme, a proto otáčení tělesa určené vektorem
 můžeme pokládat za otáčení kolem osy
procházející hmotným středem tělesa.
můžeme pokládat za otáčení kolem osy
procházející hmotným středem tělesa.
Směr osy je dán směrem vektoru
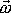 . Velikost rychlosti
. Velikost rychlosti
 je rovna součinu vzdálenosti
je rovna součinu vzdálenosti
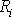 i-tého
hmotného bodu od uvažované okamžité osy otáčení tělesa a velikosti w
úhlové rychlosti otáčení;
i-tého
hmotného bodu od uvažované okamžité osy otáčení tělesa a velikosti w
úhlové rychlosti otáčení;
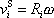 . . |
(6,67) |
Vnitřní kinetickou energii tělesa
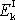 lze pak upravit na tvar
lze pak upravit na tvar
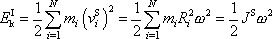 . . |
(6,68) |
Při rotaci kolem bodu se okamžitá
osa otáčení s časem mění a změní se tedy jak
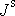 tak
tak
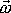 . Chceme-li vnitřní kinetickou energii
. Chceme-li vnitřní kinetickou energii
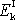 mít vyjádřenu pouze v závislosti na
změně vektoru úhlové rychlosti, musíme časově proměnné
mít vyjádřenu pouze v závislosti na
změně vektoru úhlové rychlosti, musíme časově proměnné
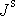 vyjádřit dle časově neproměnných složek
vyjádřit dle časově neproměnných složek
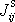 tensoru momentu setrvačnosti pro hmotný
střed tělesa. Dle
(6,60)
tensoru momentu setrvačnosti pro hmotný
střed tělesa. Dle
(6,60)
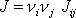 a dosadíme-li toto vyjádření za
a dosadíme-li toto vyjádření za
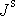 do
(6,68)
, dostáváme
do
(6,68)
, dostáváme
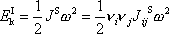 . . |
Čtverec
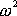 velikosti úhlové rychlosti otáčení je
veličina nezávislá na volbě soustavy souřadné, tedy
velikosti úhlové rychlosti otáčení je
veličina nezávislá na volbě soustavy souřadné, tedy
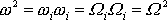 , kde
, kde
 jsou složky vektoru úhlové rychlosti
jsou složky vektoru úhlové rychlosti
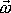 v souřadnicové soustavě spjaté
s tělesem. Veličinu
v souřadnicové soustavě spjaté
s tělesem. Veličinu
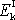 můžeme tedy dále upravit
můžeme tedy dále upravit
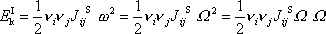 |
a jelikož dle
(6,68)
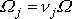 , platí
, platí
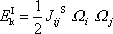 . . |
(6,69) |
Poslední rovnice je již hledaným vyjádřením vnitřní
kinetické energie
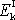 pro otáčivý pohyb tělesa kolem hmotného
středu. Rovnici
(6,69)
můžeme rozepsat a jelikož
pro otáčivý pohyb tělesa kolem hmotného
středu. Rovnici
(6,69)
můžeme rozepsat a jelikož
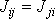 , dostaneme
, dostaneme
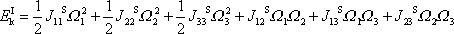 . . |
(6,69) |
Zvolíme-li soustavu souřadnic v tělese tak, že její osy
splývají se směrem hlavních os tensoru momentu setrvačnosti tedy hlavní
soustavu souřadnic, rozpis
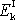 má jednodušší tvar
má jednodušší tvar
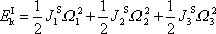 . . |
(6,69) |
Analogicky jako v rovnici
(6,60)
i zde jsme užili
zkráceného označení
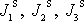 pro hlavní momenty setrvačnosti. Zde jsou to
hlavní momenty setrvačnosti vůči hlavním osám setrvačnosti procházejícím
hmotným středem tělesa.
pro hlavní momenty setrvačnosti. Zde jsou to
hlavní momenty setrvačnosti vůči hlavním osám setrvačnosti procházejícím
hmotným středem tělesa.
Je-li hmotný střed tělesa rotujícího kolem bodu
v klidu, je energie
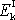 celkovou kinetickou energií tělesa
celkovou kinetickou energií tělesa
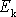 . Pro těleso, které se otáčí kolem pevné osy procházející hmotným středem, lze
tuto energii dle
(6,68)
vyjádřit jako
. Pro těleso, které se otáčí kolem pevné osy procházející hmotným středem, lze
tuto energii dle
(6,68)
vyjádřit jako
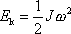 , , |
(6,70) |
kde J
je moment setrvačnosti tělesa vůči ose otáčení. Tento výsledek plyne
bezprostředně z rovnice
(5,74)
, neboť rychlost hmotného středu
 , a potom
, a potom
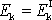 .
.
Když se těleso otáčí kolem osy, která neprochází jeho
hmotným středem, je celková kinetická energie
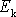 tělesa dle Königovy věty
(5,74)
dána součtem
tělesa dle Königovy věty
(5,74)
dána součtem
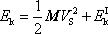 . . |
(5,74) |
Hmotný střed S tělesa je pevně svázán s tělesem, a tedy
jeho rychlost při otáčení kolem osy je dána výrazem
 , kde
, kde
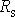 je vzdálenost hmotného středu S od osy otáčení a
je vzdálenost hmotného středu S od osy otáčení a
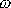 úhlová rychlost otáčení, tedy
úhlová rychlost otáčení, tedy
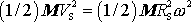 . Vnitřní kinetická energie je dle
(6,68)
. Vnitřní kinetická energie je dle
(6,68)
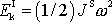 ; moment setrvačnosti uvažovaný pro vnitřní kinetickou
energii je momentem setrvačnosti vůči ose procházející hmotným středem tělesa.
Výraz
(5,74)
můžeme tak přepsat na tvar
; moment setrvačnosti uvažovaný pro vnitřní kinetickou
energii je momentem setrvačnosti vůči ose procházející hmotným středem tělesa.
Výraz
(5,74)
můžeme tak přepsat na tvar
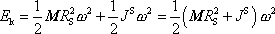 . . |
Moment setrvačnosti
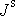 je momentem setrvačnosti vůči ose, která
prochází hmotným středem tělesa rovnoběžně s uvažovanou pevnou osou
otáčení tělesa, která v právě uvažovaném případě neprochází hmotným
středem,
je momentem setrvačnosti vůči ose, která
prochází hmotným středem tělesa rovnoběžně s uvažovanou pevnou osou
otáčení tělesa, která v právě uvažovaném případě neprochází hmotným
středem,
 je vzdálenost obou os. Dle Steinerovy věty
(6,61)
je výraz
je vzdálenost obou os. Dle Steinerovy věty
(6,61)
je výraz
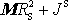 roven momentu setrvačnosti J kolem osy otáčení tělesa.
roven momentu setrvačnosti J kolem osy otáčení tělesa.
V původní formulaci Steinerovy věty (rov. (6,61) je moment setrvačnosti vůči hmotnému středu tělesa označen JS. Protože jsme v dalším rozboru uvažovali celý tenzor momentu setrvačnosti, museli jsme index S vystěhovat nahoru, aby se nepletl s indexy tenzoru. Proto je zde místo značení JS užito značení.
Tedy můžeme vyslovit závěr:
Kinetická energii tělesa, které se otáčí kolem pevné osy, vůči které má těleso moment setrvačnosti J, je dána výrazem
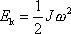 . . |
(6,70) |
Pro platnost tohoto vztahu (6,70) není důležité, zda osa otáčení prochází či neprochází hmotným středem tělesa. Z praktického hlediska je však nutno oba případy ostře odlišovat. Prochází-li osa otáčení hmotným středem (těžištěm) tělesa, má těleso charakter zobecněného kola, neprochází-li jím, jedná se o fyzické kyvadlo (viz čl. 7.2). Jak se vyvažováním snažíme zajistit, aby na osu kola nepůsobily při roztočení přídavné síly, jsme již probrali v stati 6.2.4.