V čl. 5.2 jsme nazvali otáčením tuhého tělesa kolem
pevné osy pohyb, při kterém jedna přímka pevná v tělese zachovává po celou
dobu pohybu stálou polohu v prostoru. Této přímce říkáme osa otáčení.
Pohyb tělesa otáčejícího se kolem osy je popsán, když je známa časová závislost
úhlu
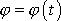 zavedeného v čl. 5.2. Najdeme rovnici, dle níž lze neznámou funkci
zavedeného v čl. 5.2. Najdeme rovnici, dle níž lze neznámou funkci
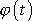 určit, tj. pohybovou rovnici tělesa, které se otáčí kolem pevné osy.
určit, tj. pohybovou rovnici tělesa, které se otáčí kolem pevné osy.
Vyjdeme z rovnice (5,49) . Pravotočivou kartézskou soustavu souřadnic pevnou v prostoru zvolíme tak, že její počátek bude ležet na ose otáčení a třetí osa bude mít směr osy otáčení. Hledanou pohybovou rovnici získáme úpravou třetí složky
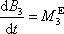 |
(6,1) |
rovnice
(5,49)
. Dle definice
(5,47)
je třetí složka
 celkového momentu hybnosti soustavy součtem
třetích složek
celkového momentu hybnosti soustavy součtem
třetích složek
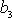 jednotlivých bodů soustavy, tj. součtem
třetích složek vektorových součinů
jednotlivých bodů soustavy, tj. součtem
třetích složek vektorových součinů
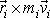 ;
;
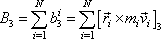 . . |
(6,2) |
Rozepíšeme třetí složku vektorového součinu
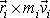 ;
;
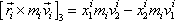 . . |
(6,3) |
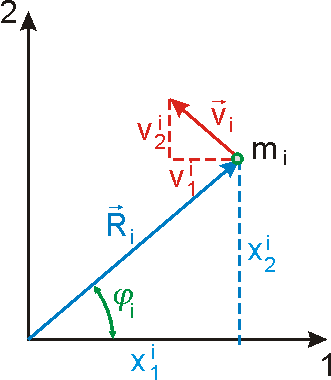 Stejně jako v článku 5.1 píšeme pořadová čísla i
bodů soustavy u souřadnic a složek rychlostí hmotných bodů nahoře
a dole píšeme číslo souřadnice. Na obr.60 je pohled ve směru a proti smyslu
třetí osy souřadnic. Je na něm znázorněn hmotný bod
Stejně jako v článku 5.1 píšeme pořadová čísla i
bodů soustavy u souřadnic a složek rychlostí hmotných bodů nahoře
a dole píšeme číslo souřadnice. Na obr.60 je pohled ve směru a proti smyslu
třetí osy souřadnic. Je na něm znázorněn hmotný bod
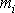 , jeho souřadnice
, jeho souřadnice
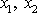 , složky jeho rychlosti
, složky jeho rychlosti
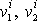 , vzdálenost bodu od osy otáčení
, vzdálenost bodu od osy otáčení
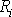 a úhel
a úhel
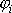 , který svírá
, který svírá
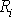 s kladným smyslem osy
s kladným smyslem osy
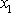 (jedná se zpravidla o úhel mimobě-žek). Vzdálenost
(jedná se zpravidla o úhel mimobě-žek). Vzdálenost
 je též poloměrem kružnice, po které se
hmotný bod
je též poloměrem kružnice, po které se
hmotný bod
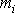 pohybuje. Zřejmě
pohybuje. Zřejmě
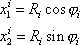 . . |
(6,4) |
Jelikož těleso nahrazujeme tuhou soustavou hmotných bodů, je
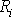 konstantní a složky rychlosti i-tého hmotného bodu jsou
konstantní a složky rychlosti i-tého hmotného bodu jsou
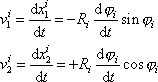 . . |
(6,5) |
Výraz
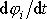 je úhlová rychlost
je úhlová rychlost
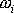 otáčení i-tého hmotného bodu. U tuhé
soustavy hmotných bodů jsou však úhlové rychlosti
otáčení i-tého hmotného bodu. U tuhé
soustavy hmotných bodů jsou však úhlové rychlosti
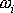 všech bodů stejné, tuhá soustava otáčející
se kolem osy má jednu úhlovou rychlost
všech bodů stejné, tuhá soustava otáčející
se kolem osy má jednu úhlovou rychlost
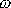 . Platí
. Platí
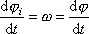 , , |
(6,6) |
kde
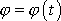 je hledaná funkce charakterizující otáčení
soustavy, za kterou můžeme volit např. některou z funkcí
je hledaná funkce charakterizující otáčení
soustavy, za kterou můžeme volit např. některou z funkcí
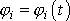 . Funkce
. Funkce
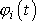 se vzájemně liší o konstantní hodnoty
odpovídající různým polohám bodů
se vzájemně liší o konstantní hodnoty
odpovídající různým polohám bodů
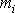 na počátku pohybu, tj. v čase
na počátku pohybu, tj. v čase
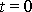 . Užijeme-li rovnic
(6,4)
a
(6,6)
, můžeme výraz
(6,3)
postupně upravit
. Užijeme-li rovnic
(6,4)
a
(6,6)
, můžeme výraz
(6,3)
postupně upravit
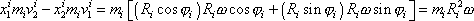 . . |
Pro třetí složku
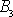 celkového momentu hybnosti danou rovnicí
(6,2)
tak dostaneme vyjádření
celkového momentu hybnosti danou rovnicí
(6,2)
tak dostaneme vyjádření
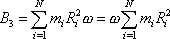 . . |
(6,7) |
Hodnota součtu
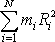 závisí pouze na hmotnostech
závisí pouze na hmotnostech
 jednotlivých hmotných bodů soustavy a na
jejich vzdálenostech
jednotlivých hmotných bodů soustavy a na
jejich vzdálenostech
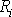 od osy otáčení. Pro tuhou soustavu hmotných
bodů, která se otáčí kolem pevné osy, je uvažovaný součet konstantní a nazýváme jej
momentem setrvačnosti J.
Definiční rovnici momentu setrvačnosti
od osy otáčení. Pro tuhou soustavu hmotných
bodů, která se otáčí kolem pevné osy, je uvažovaný součet konstantní a nazýváme jej
momentem setrvačnosti J.
Definiční rovnici momentu setrvačnosti
převedeme, dle analogie, která byla vysvětlena při úpravě rovnice (5,9) na rovnici (5,10) , pro tuhé těleso na tvar
Integrálem
(6,9)
je zaveden moment
setrvačnosti tuhého tělesa vůči pevné ose. Integruje se přes objem tělesa V,
R je proměnná vzdálenost jednotlivých bodů tělesa od osy otáčení
a
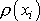 obecně proměnná hustota tělesa. Je-li těleso
homogenní, hustota nezávisí na souřadnicích
obecně proměnná hustota tělesa. Je-li těleso
homogenní, hustota nezávisí na souřadnicích
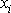 určujících polohu bodu v tělese; hustota je konstantní,
určujících polohu bodu v tělese; hustota je konstantní,
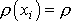 .
Příklady výpočtu a hodnoty momentů setrvačnosti homogenních těles význačného
tvaru vůči význačným osám jsou udány např. v
.
Příklady výpočtu a hodnoty momentů setrvačnosti homogenních těles význačného
tvaru vůči význačným osám jsou udány např. v
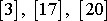 , kap.7.
, kap.7.
Se zavedeným pojmem momentu setrvačnosti můžeme rovnicí (6,1) s přihlédnutím k (6,7) psát ve tvaru
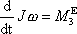 . . |
(6,10) |
Složku výsledného momentu vnějších sil
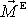 do směru osy otáčení nazýváme výsledným
momentem vnějších sil vůči ose a budeme ji označovat
do směru osy otáčení nazýváme výsledným
momentem vnějších sil vůči ose a budeme ji označovat
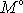 . Otáčí-li se těleso kolem třetí souřadnicové osy, je třetí složka výsledného
momentu vnější síly
. Otáčí-li se těleso kolem třetí souřadnicové osy, je třetí složka výsledného
momentu vnější síly
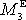 výsledným momentem vnějších sil vůči ose, můžeme ji označit
výsledným momentem vnějších sil vůči ose, můžeme ji označit
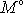 a rovnici
(6,10)
psát jako
a rovnici
(6,10)
psát jako
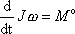 . . |
(6,11) |
Moment setrvačnosti J tuhého tělesa a tuhé soustavy hmotných bodů nezávisí na čase. Rovnici (6,11) můžeme tedy psát i takto:
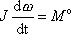 . . |
(6,12) |
Rovnice (6,11) a (6,12) jsou dva ekvivalentní tvary hledané pohybové rovnice.
Pohybová rovnice tuhého tělesa, které se otáčí kolem pevné osy
udává, že součin momentu setrvačnosti J
tělesa vůči ose otáčení a úhlového zrychlení
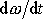 tělesa je roven výslednému momentu vůči ose
tělesa je roven výslednému momentu vůči ose
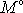 vnějších sil působících na těleso.
vnějších sil působících na těleso.
Všimneme si analogie mezi rovnicí
(2,1)
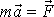 a rovnicí
(6,12)
. Obě mají tvar:
a rovnicí
(6,12)
. Obě mají tvar:
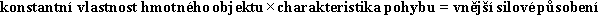 |
(6,13) |
V rovnici
(2,1)
konstantní vlastností hmotného objektu je hmotnost m,
v rovnici
(6,12)
moment setrvačnosti J.
Charakteristikou pohybu v rovnici
(2,1)
je zrychlení
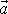 , v rovnici
(6,12)
úhlové zrychlení
, v rovnici
(6,12)
úhlové zrychlení
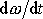 . Silové působení v rovnici
(2,1)
je dáno přímo silou
. Silové působení v rovnici
(2,1)
je dáno přímo silou
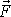 , v rovnici
(6,12)
momentem síly vůči ose
, v rovnici
(6,12)
momentem síly vůči ose
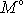 . Rovnice
(2,1)
je vektorovou rovnicí a rovnice
(6,12)
rovnicí skalární, ale
tento rozdíl není pro uvažovanou analogii podstatný.
. Rovnice
(2,1)
je vektorovou rovnicí a rovnice
(6,12)
rovnicí skalární, ale
tento rozdíl není pro uvažovanou analogii podstatný.
Pohybová rovnice
(6,12)
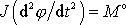 (dle
(6,6)
je
(dle
(6,6)
je
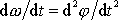 ) je diferenciální rovnicí pro určení neznámé funkce
) je diferenciální rovnicí pro určení neznámé funkce
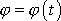 . Moment setrvačnosti J
je konstantní a lze jej pro dané těleso a pro danou osu stanovit dříve,
než začneme vyšetřovat pohyb tělesa. Výsledný moment vnějších sil vůči ose
. Moment setrvačnosti J
je konstantní a lze jej pro dané těleso a pro danou osu stanovit dříve,
než začneme vyšetřovat pohyb tělesa. Výsledný moment vnějších sil vůči ose
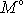 určíme tak, že vypočteme výsledný moment vnějších sil působících na těleso
určíme tak, že vypočteme výsledný moment vnějších sil působících na těleso
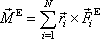 |
(5,48) |
vůči počátku soustavy souřadnic, který volíme na ose otáčení
a získaný vektor
 vynásobíme skalárně jednotkovým vektorem
vynásobíme skalárně jednotkovým vektorem
 , jenž má směr osy otáčení, tedy
, jenž má směr osy otáčení, tedy
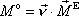 . . |
(6,14) |
Tím, jak volíme smysl vektoru
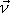 na ose otáčení, určíme, co budeme nazývat
kladným smyslem otáčení. Smysl otáčení je kladný, když
na ose otáčení, určíme, co budeme nazývat
kladným smyslem otáčení. Smysl otáčení je kladný, když
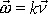 a k
je kladná konstanta,
a k
je kladná konstanta,
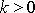 . Uvedený postup stanovení momentu
. Uvedený postup stanovení momentu
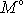 lze provést pro libovolnou orientaci osy
otáčení vůči soustavě souřadnic. Pro výše uvažované otáčení kolem třetí
souřadnicové osy má jednotkový vektor ve směru osy
lze provést pro libovolnou orientaci osy
otáčení vůči soustavě souřadnic. Pro výše uvažované otáčení kolem třetí
souřadnicové osy má jednotkový vektor ve směru osy
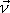 složky
složky
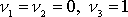 , zvolíme-li smysl
, zvolíme-li smysl
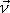 shodný s kladným smyslem třetí
souřadnicové osy. Z rovnice
(6.14)
pak dostáváme
shodný s kladným smyslem třetí
souřadnicové osy. Z rovnice
(6.14)
pak dostáváme
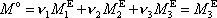 , , |
což je vztah, který jsme již uvažovali při odvození rovnic (6,11) a (6,12) .
V jednoduchých případech bývá výhodnější stanovit moment
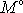 konstrukčně než právě uvedeným analytickým
postupem. Uvažujme těleso, které se otáčí kolem třetí souřadnicové osy. Vnější
síla
konstrukčně než právě uvedeným analytickým
postupem. Uvažujme těleso, které se otáčí kolem třetí souřadnicové osy. Vnější
síla
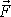 působí na těleso v bodě A, který není
bodem osy otáčení. Počátek souřadnicové soustavy leží na ose otáčení a bod A má
polohový vektor
působí na těleso v bodě A, který není
bodem osy otáčení. Počátek souřadnicové soustavy leží na ose otáčení a bod A má
polohový vektor
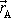 .
Průmět
.
Průmět
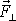 síly
síly
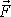 do roviny kolmé k ose otáčení je
znázorněn na obr.61a). Dle rovnic
(5,48)
a
(6,14)
příspěvek
do roviny kolmé k ose otáčení je
znázorněn na obr.61a). Dle rovnic
(5,48)
a
(6,14)
příspěvek
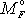 síly
síly
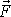 k výslednému momentu vnějších sil vůči ose je
k výslednému momentu vnějších sil vůči ose je
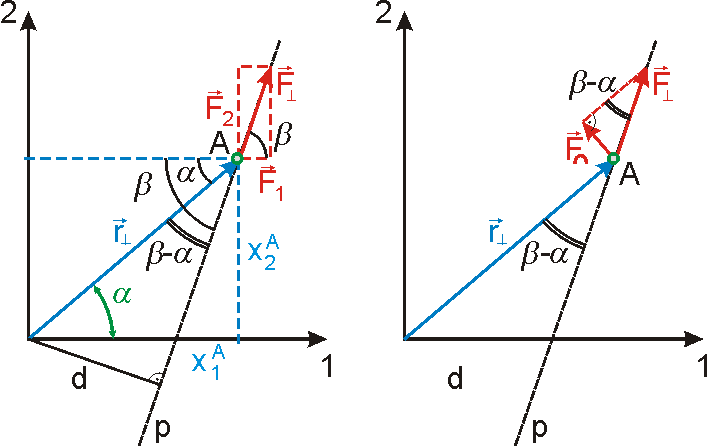
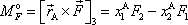 |
(6,15) |
. Průmět polohového vektoru
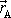 do roviny kolmé k ose otáčení označíme
do roviny kolmé k ose otáčení označíme
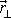 . Složkami vektoru
. Složkami vektoru
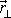 jsou prvá
jsou prvá
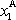 a druhá
a druhá
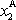 souřadnice bodu A a jeho velikost R
je rovna vzdálenosti bodu A od osy otáčení. Pro
souřadnice bodu A a jeho velikost R
je rovna vzdálenosti bodu A od osy otáčení. Pro
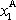 a
a
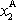 můžeme psát vyjádření
můžeme psát vyjádření
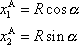 , , |
(6,16) |
kde
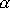 je úhel mezi vektorem
je úhel mezi vektorem
 a kladným smyslem osy
a kladným smyslem osy
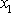 . Označíme-li
. Označíme-li
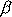 úhel mezi průmětem
úhel mezi průmětem
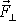 síly
síly
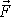 a kladným smyslem osy
a kladným smyslem osy
 , složky vektoru
, složky vektoru
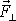 , které jsou zároveň prvými dvěma složkami vektoru
, které jsou zároveň prvými dvěma složkami vektoru
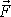 , lze vyjádřit jako
, lze vyjádřit jako
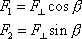 , , |
(6,17) |
kde
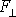 je velikost vektoru
je velikost vektoru
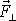 . Dosadíme-li vyjádření
(6,16)
a
(6,17)
do rovnice
(6,15)
, dostáváme
. Dosadíme-li vyjádření
(6,16)
a
(6,17)
do rovnice
(6,15)
, dostáváme
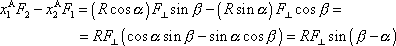 , , |
a tedy
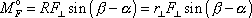 . . |
Z obr.61a)
lze vyčíst, že výraz
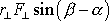 je roven vzdálenosti d přímky p
od osy otáčení, v které působí průmět
je roven vzdálenosti d přímky p
od osy otáčení, v které působí průmět
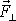 síly
síly
 . Příspěvek
. Příspěvek
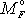 síly
síly
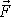 k momentu vnějších sil vůči ose je
roven součinu velikosti průmětu
k momentu vnějších sil vůči ose je
roven součinu velikosti průmětu
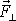 síly
síly
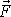 do roviny kolmé k ose otáčení a vzdálenosti d
osy otáčení od přímky p, v které průmět
do roviny kolmé k ose otáčení a vzdálenosti d
osy otáčení od přímky p, v které průmět
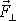 působí;
působí;
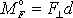 . Na obr.61 b) je znázorněna druhá možná interpretace výrazu
. Na obr.61 b) je znázorněna druhá možná interpretace výrazu
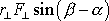 . Součin
. Součin
 je roven velikosti
je roven velikosti
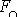 průmětu
průmětu
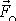 síly
síly
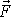 do směru kolmého k vektoru
do směru kolmého k vektoru
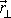 , který leží v rovině kolmé k ose otáčení. Tedy sílu
, který leží v rovině kolmé k ose otáčení. Tedy sílu
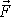 promítneme do popsaného směru a velikost
průmětu
promítneme do popsaného směru a velikost
průmětu
 vynásobíme vzdáleností
vynásobíme vzdáleností
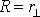 bodu A od osy otáčení, abychom získali
příspěvek
bodu A od osy otáčení, abychom získali
příspěvek
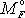 síly
síly
 k momentu
k momentu
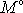 . Získané vyjádření
. Získané vyjádření
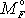 můžeme stručně zapsat,
můžeme stručně zapsat,
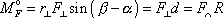 . . |
(6,18) |
Máme-li více sil
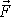 , lze jejich příspěvky
, lze jejich příspěvky
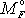 k výslednému momentu
k výslednému momentu
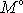 vnějších sil vůči ose sčítat. Musíme při tom
dbát toho, aby příspěvky, které se snaží otáčet tělesem v různém smyslu,
byly brány s opačným znaménkem.
vnějších sil vůči ose sčítat. Musíme při tom
dbát toho, aby příspěvky, které se snaží otáčet tělesem v různém smyslu,
byly brány s opačným znaménkem.
 Pohybová rovnice
(6,12)
pro otáčení tuhého tělesa kolem osy je velmi často užívána k řešení
konkrétních úloh. Dva příklady jejího užití ukážeme v čl. 7.2 a 7.3. Řadu
dalších lze nalézt v
Pohybová rovnice
(6,12)
pro otáčení tuhého tělesa kolem osy je velmi často užívána k řešení
konkrétních úloh. Dva příklady jejího užití ukážeme v čl. 7.2 a 7.3. Řadu
dalších lze nalézt v
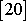 , kap. 7,
, kap. 7,
 . Zde vypočteme pohyb kladky, u které nezanedbáváme její vlastní hmotnost. Takové
kladce říkáme těžká. Je znázorněna na obr.62. Na kladce o známém momentu
setrvačnosti J a poloměru R
jsou zavěšena dvě závaží o hmotnostech
. Zde vypočteme pohyb kladky, u které nezanedbáváme její vlastní hmotnost. Takové
kladce říkáme těžká. Je znázorněna na obr.62. Na kladce o známém momentu
setrvačnosti J a poloměru R
jsou zavěšena dvě závaží o hmotnostech
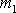 a
a
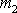 . Úsekem vlákna, na kterém je zavěšeno závaží o hmotnosti
. Úsekem vlákna, na kterém je zavěšeno závaží o hmotnosti
 , je přenášena síla o velikosti
, je přenášena síla o velikosti
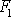 , druhým úsekem vlákna síla o velikosti
, druhým úsekem vlákna síla o velikosti
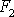 . Moment vnějších sil vůči ose otáčení o je
. Moment vnějších sil vůči ose otáčení o je
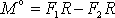 ; smysl otáčení, kdy závaží o hmotnosti
; smysl otáčení, kdy závaží o hmotnosti
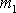 klesá, pokládáme za kladný. Závaží
o hmotnosti
klesá, pokládáme za kladný. Závaží
o hmotnosti
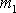 klesá se zrychlením a.
Dle rovnice
(2,1)
musí platit
klesá se zrychlením a.
Dle rovnice
(2,1)
musí platit
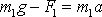 , kde
, kde
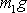 je tíha hmotnosti
je tíha hmotnosti
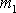 . Tedy
. Tedy
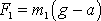 . Obdobně pro hmotnost
. Obdobně pro hmotnost
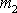 , která stoupá se zrychlením a, platí
, která stoupá se zrychlením a, platí
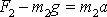 , a tedy
, a tedy
 . Dosadíme-li získanou hodnotu momentu
. Dosadíme-li získanou hodnotu momentu
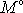 do rovnice
(6,12)
, dostaneme
do rovnice
(6,12)
, dostaneme
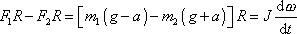 . . |
(6,19) |
Úhlová rychlost
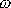 kladky a postupná rychlost v
závaží o hmotnosti
kladky a postupná rychlost v
závaží o hmotnosti
 jsou vázány vztahem
jsou vázány vztahem
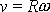 . Derivujeme-li rovnici
. Derivujeme-li rovnici
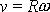 dle času t, získáme vztah mezi
postupným zrychlením a bodu
dle času t, získáme vztah mezi
postupným zrychlením a bodu
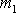 a úhlovým zrychlením
a úhlovým zrychlením
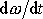 kladky
kladky
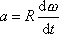 . . |
Dosadíme-li za
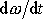 do rovnice
(6,19)
, dostáváme po úpravě
do rovnice
(6,19)
, dostáváme po úpravě
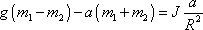 , , |
odkud
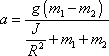 . . |
Zrychlení a je konstantní, tedy též úhlové zrychlení
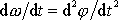 , které, jak jsme ukázali, je rovno
, které, jak jsme ukázali, je rovno
 , je konstantní. Pro časovou závislost úhlu
, je konstantní. Pro časovou závislost úhlu
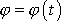 popisujícího otáčení kladky pak integrací dostáváme
popisujícího otáčení kladky pak integrací dostáváme
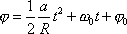 , , |
kde
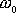 je úhlová rychlost otáčení kladky
v čase
je úhlová rychlost otáčení kladky
v čase
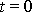 a
a
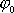 je úhel
je úhel
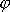 v čase
v čase
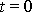 .
.
Mějme soustavu hmotných bodů, pro které moment vnějších sil
vůči jisté ose je nulový. Touto osou proložíme třetí osu soustavy souřadnic.
Potom třetí složka
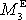 výsledného momentu vnějších sil působících na soustavu je nulová,
výsledného momentu vnějších sil působících na soustavu je nulová,
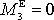 , a dle rovnice
(6,1)
také
, a dle rovnice
(6,1)
také
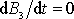 . Je-li
. Je-li
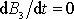 , je třetí složka
, je třetí složka
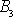 celkového momentu hybnosti soustavy
konstantní,
celkového momentu hybnosti soustavy
konstantní,
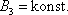 . . |
(6,20) |
Třetí složka
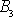 momentu hybnosti je dána rovnicí
(6,2)
,
jeden sčítanec součtu tvořícího
momentu hybnosti je dána rovnicí
(6,2)
,
jeden sčítanec součtu tvořícího
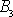 rovnicí
(6,3)
. O soustavě hmotných bodů
nebudeme předpokládat, že je tuhá. Souřadnice
rovnicí
(6,3)
. O soustavě hmotných bodů
nebudeme předpokládat, že je tuhá. Souřadnice
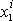 a
a
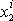 hmotných bodů volné soustavy můžeme také vyjádřit rovnicemi
(6,4)
hmotných bodů volné soustavy můžeme také vyjádřit rovnicemi
(6,4)
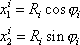 . . |
(6,4) |
Jelikož však soustava nemusí být tuhá, budeme pokládat za funkci času nejen
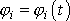 , ale i vzdálenost --tého bodu od osy otáčení
, ale i vzdálenost --tého bodu od osy otáčení
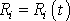 . Pro složky rychlosti
. Pro složky rychlosti
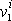 a
a
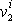 pak derivováním rovnic
(6,4)
získáme vyjádření
pak derivováním rovnic
(6,4)
získáme vyjádření
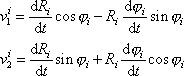 . . |
(6,21) |
Dosadíme-li (6,4) a (6,21) do (6,3) , dostáváme
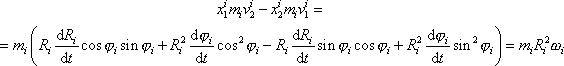 |
a dle
(6,2)
můžeme pak
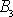 psát jako
psát jako
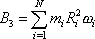 . . |
(6,22) |
Rovnice
(6,22)
je sice formálně
podobná rovnici
(6,7)
, ale jelikož se neomezujeme na tuhou soustavu hmotných
bodů, je
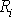 v rovnici
(6,22)
obecně funkcí času a
v rovnici
(6,22)
obecně funkcí času a
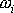 může být různé pro jednotlivé hmotné body soustavy. Uvažujeme případ
(6,20)
může být různé pro jednotlivé hmotné body soustavy. Uvažujeme případ
(6,20)
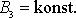 , a tedy
, a tedy
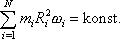 . . |
(6,23) |
Rovnice (6,23) je obecnou formulací zákona zachování momentu hybnosti pro volné soustavy, které lze pokládat za soustavy otáčející se kolem pevné osy.
Dle rovnice
(6,23)
můžeme např. řešit pohyb soustavy, která
se skládá z jednoho nebo více hmotných bodů pohybujících se vůči kotouči
otáčejícímu se kolem pevné osy. Výsledný moment vnějších sil působících na
kotouč a hmotné body musí být nulový. Člen
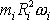 součtu
(6,23)
odpovídající kotouči nahradíme
součinem momentu setrvačnosti kotouče J
a jeho úhlové rychlosti otáčení
součtu
(6,23)
odpovídající kotouči nahradíme
součinem momentu setrvačnosti kotouče J
a jeho úhlové rychlosti otáčení
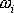 . Pokládáme-li člen odpovídající kotouči za první člen součtu
(6,23)
, označíme
jeho rychlost
. Pokládáme-li člen odpovídající kotouči za první člen součtu
(6,23)
, označíme
jeho rychlost
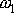 a součet
(6,23)
můžeme psát ve tvaru
a součet
(6,23)
můžeme psát ve tvaru
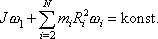 , , |
(6,24) |
kde N
je celkový počet prvků soustavy včetně kotouče. Známe-li pohyb hmotných
bodů vůči kotouči, známe časovou závislost hodnot
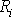 a
a
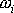 a z rovnice
(6,24)
můžeme pak určit,
jak se s časem změní úhlová rychlost
a z rovnice
(6,24)
můžeme pak určit,
jak se s časem změní úhlová rychlost
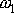 kotouče.
kotouče.
Často se uvažuje příklad, kdy osoba chodí po otáčejícím se kotouči. Na přednáškách provádíme demonstrační pokus, při kterém elektrický vláček jezdí po kolejích umístěných na obvodu točny volně se otáčející v ložiskách. Na stejné točně se nechá v radiálním směru jezdit elektricky poháněný a ovládaný traktůrek. Při rozjezdu vláčku se točna začne otáčet v opačném smyslu než vláček. Při zastavení se zastaví nejen vláček, ale i točna. Když traktůrek jede ke středu otáčející se točny, otáčení se zrychluje, když jede od středu, otáčení se zpomaluje. Lze demonstrovat i další situace potvrzující zachování momentu hybnosti soustavy při prováděném pokusu.
Ze zákona zachování momentu hybnosti nikterak neplyne, že je splněn též zákon zachování energie. Pohybuje-li se na otáčejícím se kotouči osoba z okraje do středu, musí překonávat odstředivou sílu a koná tedy prácí. Práce se projeví zvýšením kinetické energie (6,70) soustavy (na vodorovném kotouči se potenciální energie nemění).
Vnitřními silami nelze měnit hybnost ani moment hybnosti soustavy, ale lze měnit její energii.
Někdy lze uvažovanou volnou soustavu hmotných bodů
v určitých fázích pohybu pokládat za tuhou soustavu. Nechť osoba sedící na
otáčivé židli rozpaží ruce, v kterých má činky. Před rozpažením rukou
můžeme osobu, činky a židli pokládat za tuhou soustavu otáčející se společnou
úhlovou rychlostí
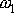 . Při rozpažování rukou není soustava tuhá. Má-li již osoba rozpaženo, znovu
můžeme soustavu pokládat za tuhou s úhlovou rychlostí otáčení
. Při rozpažování rukou není soustava tuhá. Má-li již osoba rozpaženo, znovu
můžeme soustavu pokládat za tuhou s úhlovou rychlostí otáčení
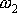 . Obecně, můžeme-li na počátku pohybu soustavu pokládat za tuhou, jsou
v součtu
(6,22)
. Obecně, můžeme-li na počátku pohybu soustavu pokládat za tuhou, jsou
v součtu
(6,22)
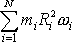 všechna
všechna
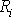 konstantní a
konstantní a
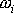 pro všechny body stejné. Společnou
hodnotu
pro všechny body stejné. Společnou
hodnotu
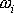 označíme
označíme
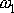 a součet
a součet
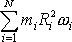 píšeme jako
píšeme jako
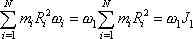 . . |
(6,25) |
Konstantní hodnotu
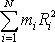 ve shodě s
(6,8)
pokládáme za moment setrvačnosti
ve shodě s
(6,8)
pokládáme za moment setrvačnosti
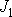 soustavy. Lze-li po přeskupení bodů soustavu
znovu pokládat za tuhou soustavu otáčející se okolo původní osy otáčení, můžeme
výraz
soustavy. Lze-li po přeskupení bodů soustavu
znovu pokládat za tuhou soustavu otáčející se okolo původní osy otáčení, můžeme
výraz
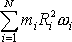 přepsat na tvar
přepsat na tvar
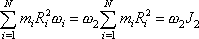 , , |
(6,26) |
kde
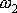 je nová úhlová rychlost otáčení a
je nová úhlová rychlost otáčení a
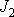 nový moment setrvačnosti soustavy. Dle
rovnice
(6,23)
musí se výrazy
(6,25)
a
(6,26)
sobě rovnat, tedy
nový moment setrvačnosti soustavy. Dle
rovnice
(6,23)
musí se výrazy
(6,25)
a
(6,26)
sobě rovnat, tedy
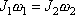 . . |
(6,27) |
Poslední rovnice je obvyklou formulací zákona zachování momentu hybnosti (5,61) pro soustavu, kterou lze v právě vyloženém smyslu chápat jako soustavu otáčející se kolem pevné osy.
Opakujeme, že podmínkou platnosti
rovnice
(6,27)
je nulová hodnota výsledného momentu vnějších sil vůči ose
otáčení. Dle rovnice
(6,27)
lze např. vysvětlit zmenšení úhlové rychlosti
otáčení, rozpaží-li osoba na otáčivé židli ruce nebo zvětšení úhlové rychlosti
otáčení krasobruslaře při piruetě. Osoba s rozpaženýma rukama má větší
moment setrvačnosti
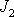 , než je její moment setrvačnosti
, než je její moment setrvačnosti
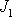 , má-li ruce připažené. Z rovnice
(6,27)
pak plyne že pro
, má-li ruce připažené. Z rovnice
(6,27)
pak plyne že pro
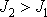 je
je
 . Řadu příkladů na právě probraný zákon zachování momentu hybnosti lze nalézt. v
. Řadu příkladů na právě probraný zákon zachování momentu hybnosti lze nalézt. v
 , kap.6.
, kap.6.