V článku 5.3 jsme ukázali, že věta o hybnosti soustavy (5,33) , případně její úprava (5,35) a věta o momentu hybnosti soustavy (5,49) jsou výchozími rovnicemi dynamiky tuhého tělesa. V těchto rovnicích je silové působení na tuhé těleso vystiženo výslednicí vnějších sil působících na těleso
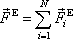 |
(5,32) |
a výsledným momentem vnějších sil působících na těleso
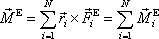 . . |
(5,48) |
Různé soustavy vnějších sil působících na těleso, jejichž
výslednice
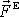 a výsledný moment
a výsledný moment
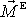 vzhledem k témuž bodu jsou stejné, mají
stejný dynamický účinek na těleso. O takových soustavách sil říkáme, že jsou
dynamicky ekvivalentní.
vzhledem k témuž bodu jsou stejné, mají
stejný dynamický účinek na těleso. O takových soustavách sil říkáme, že jsou
dynamicky ekvivalentní.
 Nejprve ukážeme, jak závisí výsledný moment vnějších sil
Nejprve ukážeme, jak závisí výsledný moment vnějších sil
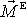 na volbě bodu, vůči kterému jej počítáme.
Budeme předpokládat, že moment je vyjádřen výrazem
na volbě bodu, vůči kterému jej počítáme.
Budeme předpokládat, že moment je vyjádřen výrazem
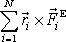 a je tedy počítán vůči počátku souřadnicové
soustavy. Počátek souřadnicové soustavy, v které je počítán moment
a je tedy počítán vůči počátku souřadnicové
soustavy. Počátek souřadnicové soustavy, v které je počítán moment
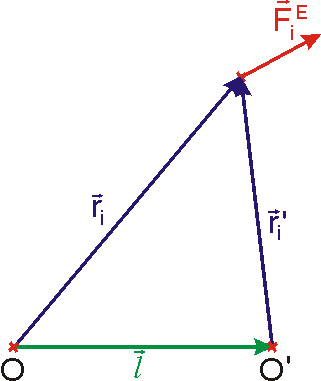
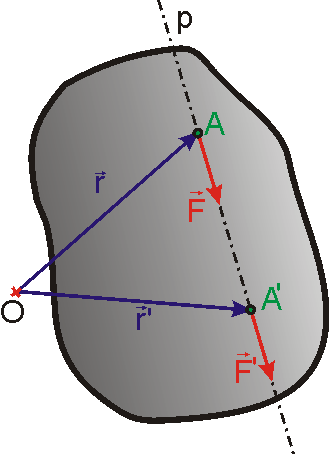
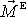 , označíme O (viz obr.49). Nyní posuneme počátek soustavy souřadné o vektor
, označíme O (viz obr.49). Nyní posuneme počátek soustavy souřadné o vektor
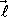 tak, že nový počátek se nachází v místě O.
Určíme vztah výsledného momentu
tak, že nový počátek se nachází v místě O.
Určíme vztah výsledného momentu
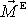 vnějších sil působících na soustavu
počítaného vůči bodu O, k výslednému momentu
vnějších sil působících na soustavu
počítaného vůči bodu O, k výslednému momentu
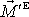 vnějších sil počítanému vůči bodu O .
Mezi polohovými vektory hmotných bodů
vnějších sil počítanému vůči bodu O .
Mezi polohovými vektory hmotných bodů
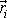 v soustavě souřadné s počátkem
v bodě O a polohovými vektory
v soustavě souřadné s počátkem
v bodě O a polohovými vektory
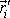 v soustavě souřadné s počátkem
v bodě O platí vztah
v soustavě souřadné s počátkem
v bodě O platí vztah
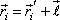 . . |
(5,96) |
Vektor
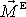 je dán vztahem
(5,48)
,
je dán vztahem
(5,48)
,
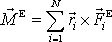 ,vektor
,vektor
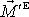 rovnicí
rovnicí
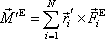 . . |
(5,97) |
Dosadíme-li do
(5,97)
za
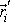 z
(5,96)
, dostáváme postupně
z
(5,96)
, dostáváme postupně
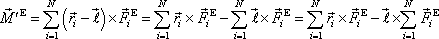 . . |
S přihlédnutím k rovnicím (5,32) a (5,48) můžeme výsledek stručně zapsat jako
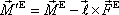 |
(5,98) |
a získáváme tak hledaný vztah mezi
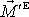 a
a
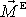 .
.
Změníme-li počátek souřadnicové soustavy, vůči kterému
počítáme výsledný moment vnějších sil působících na těleso, musíme od původního
momentu
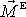 odečíst vektorový součin vektoru
odečíst vektorový součin vektoru
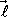 , o který jsme počátek posunuli, a výslednice vnějších sil
, o který jsme počátek posunuli, a výslednice vnějších sil
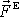 , abychom dostali vyjádření výsledného momentu vnějších sil
, abychom dostali vyjádření výsledného momentu vnějších sil
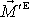 v nové soustavě souřadnic. Změna
počátku neovlivní výslednici vnějších sil
v nové soustavě souřadnic. Změna
počátku neovlivní výslednici vnějších sil
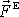 .
.
 Mějme tuhé těleso a na něj v místech
Mějme tuhé těleso a na něj v místech
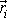 (i= 1, 2, ,N) působící vnější
síly
(i= 1, 2, ,N) působící vnější
síly
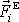 . Přímý a často také nejjednodušší postup jak zjistit dynamický účinek těchto sil
je vypočítat dle
(5,32)
výslednici
. Přímý a často také nejjednodušší postup jak zjistit dynamický účinek těchto sil
je vypočítat dle
(5,32)
výslednici
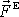 sil
sil
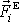 a dle rovnice
(5,48)
výsledný moment
a dle rovnice
(5,48)
výsledný moment
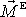 sil
sil
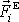 vzhledem k zvolenému počátku
souřadnicové soustavy. Jelikož stanovení účinku sil působících na těleso má
řadu technických aplikací, především při řešení statických úloh, kde často není
třeba řešit problém stanovení
vzhledem k zvolenému počátku
souřadnicové soustavy. Jelikož stanovení účinku sil působících na těleso má
řadu technických aplikací, především při řešení statických úloh, kde často není
třeba řešit problém stanovení
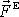 a
a
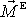 v plné obecnosti, rozvinula se řada
metod, jak nahrazovat složitější systémy sil působících na těleso dynamicky
ekvivalentními soustavami jednoduššími. S těmito metodami jste se již
seznámili v dřívějším studiu (viz [1]) a podrobně bývají
popsány v technicky zaměřených učebnicích mechaniky. Zde objasníme jen
některé nejdůležitější postupy.
v plné obecnosti, rozvinula se řada
metod, jak nahrazovat složitější systémy sil působících na těleso dynamicky
ekvivalentními soustavami jednoduššími. S těmito metodami jste se již
seznámili v dřívějším studiu (viz [1]) a podrobně bývají
popsány v technicky zaměřených učebnicích mechaniky. Zde objasníme jen
některé nejdůležitější postupy.
Působí-li v místě A o polohovém vektoru
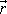 na těleso síla
na těleso síla
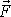 , lze ji přenést do libovolného jiného působiště podél přímky p,
která prochází bodem A ve směru vektoru síly
, lze ji přenést do libovolného jiného působiště podél přímky p,
která prochází bodem A ve směru vektoru síly
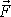 (viz obr.50). Pro přímku p užíváme označení
vektorová přímka. Účinek síly na těleso se nemění, když její
působiště posuneme podél vektorové přímky. Síla
(viz obr.50). Pro přímku p užíváme označení
vektorová přímka. Účinek síly na těleso se nemění, když její
působiště posuneme podél vektorové přímky. Síla
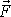 v bodě A´ o polohovém vektoru
v bodě A´ o polohovém vektoru
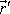 , přispěje do součtu sil
(5,32)
a do součtu momentů sil
(5,48)
stejně jako síla
, přispěje do součtu sil
(5,32)
a do součtu momentů sil
(5,48)
stejně jako síla
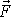 v bodě A o polohovém vektoru
v bodě A o polohovém vektoru
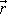 (původní působiště síly). Vektor
(původní působiště síly). Vektor
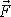 je v obou polohách stejný a platí i rovnost momentů
je v obou polohách stejný a platí i rovnost momentů
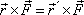 . . |
(5,99) |
Vektory
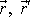 a
a
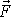 leží v jedné rovině, vektory
leží v jedné rovině, vektory
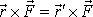 jsou rovnoběžné. Posunutím vektoru
jsou rovnoběžné. Posunutím vektoru
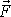 po přímce p se nemůže změnit smysl vektorového součinu, a proto vektory
po přímce p se nemůže změnit smysl vektorového součinu, a proto vektory
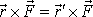 mají nejen stejný směr, ale i stejný smysl. Velikosti vektorů
mají nejen stejný směr, ale i stejný smysl. Velikosti vektorů
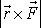 a
a
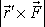 jsou stejné, jak bylo ukázáno při definici
(3,32)
momentu síly. Velikost momentu je rovna velikosti síly násobené kolmou
vzdáleností bodu, vůči kterému moment počítáme, od přímky, v které působí
síla
jsou stejné, jak bylo ukázáno při definici
(3,32)
momentu síly. Velikost momentu je rovna velikosti síly násobené kolmou
vzdáleností bodu, vůči kterému moment počítáme, od přímky, v které působí
síla
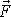 . V našem případě je uvažovanou vzdáleností vzdálenost bodu O od přímky p,
a ta je pro oba momenty stejná. Tedy vskutku platí vektorová rovnost
(5,99)
.
. V našem případě je uvažovanou vzdáleností vzdálenost bodu O od přímky p,
a ta je pro oba momenty stejná. Tedy vskutku platí vektorová rovnost
(5,99)
.
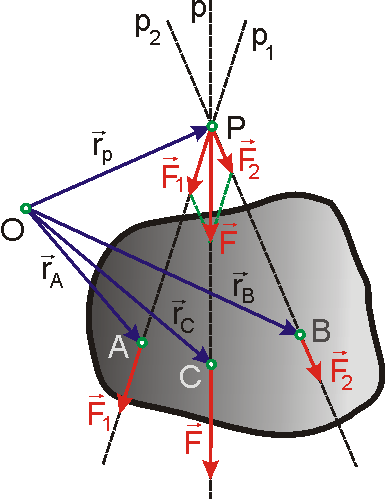 Na obr.51 je znázorněna další často uvažovaná
konstrukce pro skládání dvou sil působících na těleso, jejichž vektorové
přímky
Na obr.51 je znázorněna další často uvažovaná
konstrukce pro skládání dvou sil působících na těleso, jejichž vektorové
přímky
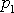 a
a
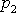 jsou různoběžné. Síly
jsou různoběžné. Síly
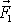 a
a
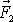 působící v bodech A a B můžeme, jak
bylo ukázáno, posunout do průsečíku P jejich vektorových přímek
působící v bodech A a B můžeme, jak
bylo ukázáno, posunout do průsečíku P jejich vektorových přímek
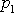 a
a
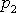 .
V průsečíku P síly vektorově složíme, získáme sílu
.
V průsečíku P síly vektorově složíme, získáme sílu
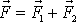 , kterou může-me libovolně posunout podél její vektorové přímky p
např. do bodu C, který je naznačen na obr.51. Nahradíme-li síly
, kterou může-me libovolně posunout podél její vektorové přímky p
např. do bodu C, který je naznačen na obr.51. Nahradíme-li síly
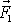 a
a
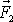 silou
silou
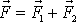 , nemá tato záměna zřejmě žádný vliv na součet
(5,32)
. Moment síly
, nemá tato záměna zřejmě žádný vliv na součet
(5,32)
. Moment síly
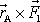 , je-li síla
, je-li síla
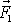 v bodě A, je stejný jako moment
v bodě A, je stejný jako moment
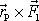 síly
síly
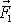 v bodě P, jak jsme již zdůvodnili u rovnosti
(5,99)
. Obdobně moment
v bodě P, jak jsme již zdůvodnili u rovnosti
(5,99)
. Obdobně moment
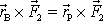 . Jelikož pro vektorový součin platí distributivní zákon,
. Jelikož pro vektorový součin platí distributivní zákon,
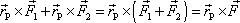 . . |
Posuneme-li sílu
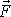 do bodu C, musí znovu platit
do bodu C, musí znovu platit
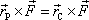 . . |
Shrneme-li získané výsledky, dostáváme
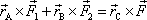 . . |
Součet momentů sil
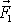 v bodě A a
v bodě A a
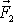 v bodě B vůči bodu O je stejný jako
monet síly
v bodě B vůči bodu O je stejný jako
monet síly
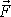 v místě C vůči témuž bodu O. Nahrazení
dvou sil
v místě C vůči témuž bodu O. Nahrazení
dvou sil
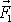 a
a
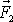 jednou silou
jednou silou
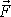 postupem naznačeným na obr.51 nemá tedy
žádný vliv ani na součet momentů sil
(5,48)
. Síla
postupem naznačeným na obr.51 nemá tedy
žádný vliv ani na součet momentů sil
(5,48)
. Síla
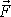 v bodě C a dvě síly
v bodě C a dvě síly
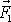 v bodě A a
v bodě A a
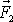 v bodě B jsou dynamicky ekvivalentní.
Podobným způsobem lze vysvětlit oprávněnost dalších vám známých (viz [1])
konstrukcí, např. konstrukce pro skládání dvou souhlasně a nesouhlasně
rovnoběžných sil.
v bodě B jsou dynamicky ekvivalentní.
Podobným způsobem lze vysvětlit oprávněnost dalších vám známých (viz [1])
konstrukcí, např. konstrukce pro skládání dvou souhlasně a nesouhlasně
rovnoběžných sil.
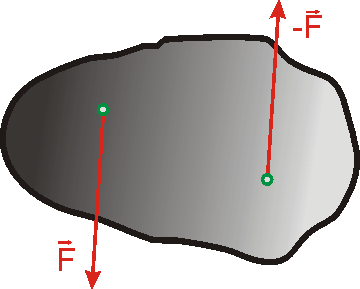 Konstrukčně neřešitelný případ skládání dvou sil nastane, je-li třeba složit dvě stejně
velké síly stejného směru, ale opačného smyslu (nesouhlasně rovnoběžné)
působící v různých místech tuhého tělesa (viz obr.52). Při konstrukci
nahrazujeme dvě síly
Konstrukčně neřešitelný případ skládání dvou sil nastane, je-li třeba složit dvě stejně
velké síly stejného směru, ale opačného smyslu (nesouhlasně rovnoběžné)
působící v různých místech tuhého tělesa (viz obr.52). Při konstrukci
nahrazujeme dvě síly
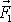 a
a
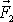 jednou, vhodně položenou silou
jednou, vhodně položenou silou
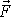 , která je rovna součtu sil
, která je rovna součtu sil
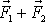 .
.
Jsou-li dvě síly stejně velké a nesouhlasně rovnoběžné, je jejich součet nulový,
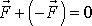 a obvyklý konstrukční postup nelze provést.
Takové dvě síly, nepůsobí-li podél stejné vektorové přímky p,
jsou nejjednodušší soustavou sil, pro kterou součet sil
(5,32)
je nulový, ale
součet momentů
(5,48)
je nenulový. Působí-li taková soustava sil znázorněná na
obr.52 na těleso, říkáme, že na těleso působí
dvojice sil. Spočteme příspěvek dvojice sil do součtu momentů
(5,48)
. Nachází-li se síla
a obvyklý konstrukční postup nelze provést.
Takové dvě síly, nepůsobí-li podél stejné vektorové přímky p,
jsou nejjednodušší soustavou sil, pro kterou součet sil
(5,32)
je nulový, ale
součet momentů
(5,48)
je nenulový. Působí-li taková soustava sil znázorněná na
obr.52 na těleso, říkáme, že na těleso působí
dvojice sil. Spočteme příspěvek dvojice sil do součtu momentů
(5,48)
. Nachází-li se síla
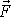 v místě A o polohovém vektoru
v místě A o polohovém vektoru
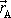 , její moment vůči počátku O soustavy souřadnic je
, její moment vůči počátku O soustavy souřadnic je
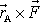 a obdobně moment síly
a obdobně moment síly
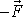 působící v bodě B je
působící v bodě B je
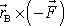 (viz obr.53). Tyto dva sčítance přispívají do součtu
(5,48)
výrazem
(viz obr.53). Tyto dva sčítance přispívají do součtu
(5,48)
výrazem
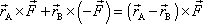 , , |
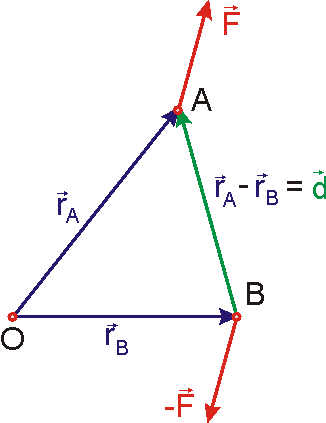 který nazveme momentem dvojice sil
který nazveme momentem dvojice sil
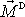 . Vektor
. Vektor
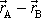 označíme
označíme
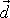 . Vektor
. Vektor
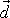 spojuje působiště obou sil, přičemž jeho
smysl volíme tak, aby směřoval k působišti té z obou sil, s níž
vektorovým násobením v pořadí
spojuje působiště obou sil, přičemž jeho
smysl volíme tak, aby směřoval k působišti té z obou sil, s níž
vektorovým násobením v pořadí
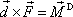 |
(5,100) |
vytvoří moment dvojice sil. Změníme-li počátek soustavy
souřadné, tj. zaměníme-li bod O nějakým jiným bodem O , vektor
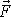 ani vektor
ani vektor
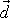 se nezmění. Na rozdíl od momentu síly
nemusíme u momentu silové dvojice uvažovat o bodu, vůči kterému je počítán.
Analogicky důkazu (viz čl.3.7), že velikost momentu síly je rovna velikosti
síly násobené kolmou vzdáleností její vektorové přímky od bodu, vůči kterému
moment počítáme, lze dokázat, že velikost
se nezmění. Na rozdíl od momentu síly
nemusíme u momentu silové dvojice uvažovat o bodu, vůči kterému je počítán.
Analogicky důkazu (viz čl.3.7), že velikost momentu síly je rovna velikosti
síly násobené kolmou vzdáleností její vektorové přímky od bodu, vůči kterému
moment počítáme, lze dokázat, že velikost
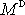 momentu
momentu
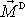 je rovna součinu velikosti F jedné ze sil tvořící dvojici a kolmé
vzdálenosti
je rovna součinu velikosti F jedné ze sil tvořící dvojici a kolmé
vzdálenosti
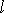 rovnoběžných vektorových přímek obou sil,
rovnoběžných vektorových přímek obou sil,
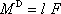 . . |
(5,101) |
Po zavedení pojmu moment dvojice sil můžeme vyslovit další pravidlo o skládání sil působících na těleso:
Přeneseme-li sílu
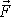 z bodu A do bodu B, její dynamický účinek na těleso se nezmění, přidáme-li k síle
z bodu A do bodu B, její dynamický účinek na těleso se nezmění, přidáme-li k síle
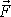 v bodu B silovou dvojici o momentu
v bodu B silovou dvojici o momentu
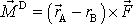 .
.
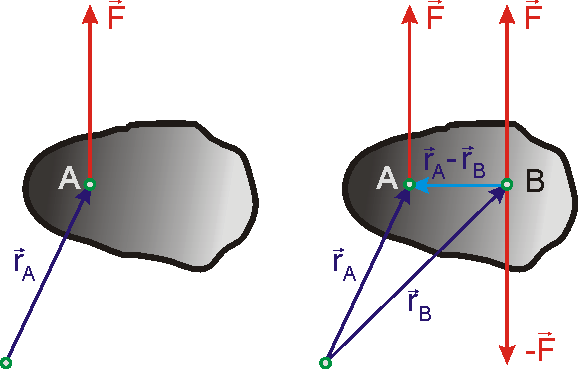 Na obr.54 a) je znázorněna síla
Na obr.54 a) je znázorněna síla
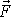 v bodě A, na obr. 54 b) síla
v bodě A, na obr. 54 b) síla
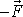 v bodě B a dvojice sil kompenzující
přenesení síly z bodu A do bodu B. Výsledný příspěvek soustavy na
obr.54 a) k výslednici sil
(5,32)
je stejný jako příspěvek soustavy z obr.54 b) a rovná se
v bodě B a dvojice sil kompenzující
přenesení síly z bodu A do bodu B. Výsledný příspěvek soustavy na
obr.54 a) k výslednici sil
(5,32)
je stejný jako příspěvek soustavy z obr.54 b) a rovná se
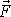 . K výslednému momentu vnějších sil
(5,48)
přispívá soustava
z obr.54 a) výrazem
. K výslednému momentu vnějších sil
(5,48)
přispívá soustava
z obr.54 a) výrazem
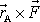 a soustava z obr.54 b) výrazem, který lze rozepsat jako
součet momentu dvojice sil
a soustava z obr.54 b) výrazem, který lze rozepsat jako
součet momentu dvojice sil
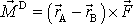 a momentu
a momentu
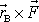 síly
síly
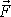 v bodě B. Protože vektorový součin je
distributivní, zřejmě platí, že oba výrazy jsou stejné
;
v bodě B. Protože vektorový součin je
distributivní, zřejmě platí, že oba výrazy jsou stejné
;
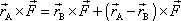 . . |
Soustavy na obr.54 a) a 54 b) přispívají stejně jak
k výslednici sil
(5,32)
, tak i k výslednému momentu sil
(5,48)
, a
jsou tedy dynamicky ekvivalentní. K tomuto závěru lze dojít přímo z názoru,
neboť síly
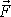 a
a
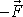 v bodě B se ruší a s nulovou silou
v bodě B je soustava 54 b)
zřejmě stejná jako soustava 54 a).
v bodě B se ruší a s nulovou silou
v bodě B je soustava 54 b)
zřejmě stejná jako soustava 54 a).
Právě probraným postupem můžeme přenést všechny síly
působící na těleso do hmotného středu tělesa. Působí-li v místech
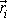 na těleso vnější síly
na těleso vnější síly
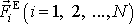 , bude po přenesení v hmotném středu, jehož polohový vektor označíme
, bude po přenesení v hmotném středu, jehož polohový vektor označíme
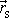 , působit všech N sil
, působit všech N sil
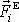 . Pro kompenzaci přenesení musíme připojit N
momentů dvojic sil
. Pro kompenzaci přenesení musíme připojit N
momentů dvojic sil
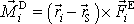 . Přenesením sil
. Přenesením sil
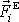 se zřejmě nezmění jejich součet
se zřejmě nezmění jejich součet
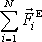 , a tedy výslednice vnějších sil působících na soustavu
(5,32)
je pro původní i
konečnou soustavu stejná. Součet
, a tedy výslednice vnějších sil působících na soustavu
(5,32)
je pro původní i
konečnou soustavu stejná. Součet
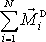 momentů dvojic sil
momentů dvojic sil
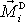 nazveme momentem výsledné silové dvojice. Můžeme jej vyjádřit jako
nazveme momentem výsledné silové dvojice. Můžeme jej vyjádřit jako
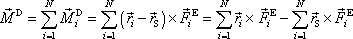 . . |
Uvědomíme-li si, že
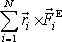 je součet
(5,48)
, tj. výsledný moment
je součet
(5,48)
, tj. výsledný moment
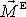 vnějších sil působících na těleso, a že se nesčítá přes
vnějších sil působících na těleso, a že se nesčítá přes
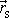 , můžeme poslední rovnici upravit na tvar
, můžeme poslední rovnici upravit na tvar
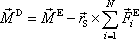 . . |
(5,102) |
Na základě rovnice
(5,102)
můžeme říci, že výsledný moment
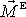 vnějších sil působících na soustavu je roven momentu
vnějších sil působících na soustavu je roven momentu
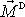 výsledné dvojice sil zvětšenému o moment výslednice vnějších sil
výsledné dvojice sil zvětšenému o moment výslednice vnějších sil
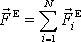 umístěné v hmotném středu soustavy.
Tedy přenesením sil do hmotného středu a přidáním kompenzujících momentů
silových dvojic se nezmění výsledný moment
(5,48)
vnějších sil působících na
soustavu. Jelikož jsme již ukázali neměnnost součtu
(5,32)
, dokázali jsme, že
nová soustava po přidání momentu výsledné silové dvojice je dynamicky
ekvivalentní s původní soustavu, kdy síly
umístěné v hmotném středu soustavy.
Tedy přenesením sil do hmotného středu a přidáním kompenzujících momentů
silových dvojic se nezmění výsledný moment
(5,48)
vnějších sil působících na
soustavu. Jelikož jsme již ukázali neměnnost součtu
(5,32)
, dokázali jsme, že
nová soustava po přidání momentu výsledné silové dvojice je dynamicky
ekvivalentní s původní soustavu, kdy síly
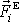 se nacházely v místech
se nacházely v místech
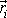 .
.
Posuneme-li bod, vůči kterému počítáme výsledný moment vnějších sil působících na soustavu, do hmotného středu soustavy, dostáváme dle (5,98)
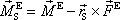 |
(5,103) |
a porovnání rovnic (5,103) a (5,102) dá výsledek
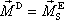 . . |
(5,104) |
Výsledný moment vnějších sil působících na těleso počítaný
vůči hmotnému středu soustavy
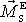 je roven momentu výsledné silové dvojice
působící na těleso. Je-li speciálně výsledná vnější síla
je roven momentu výsledné silové dvojice
působící na těleso. Je-li speciálně výsledná vnější síla
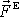 působící na těleso rovna nule, je dle
(5,98)
výsledný moment vnějších sil
působící na těleso rovna nule, je dle
(5,98)
výsledný moment vnějších sil
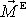 nezávislý na volbě bodu, vůči kterému je
počítán a dle rovnice
(5,102)
je roven momentu výsledné dvojice sil.
nezávislý na volbě bodu, vůči kterému je
počítán a dle rovnice
(5,102)
je roven momentu výsledné dvojice sil.
Ukážeme, proč se pro hmotný střed tělesa užívá též názvu
těžiště. Mějme soustavu hmotných bodů
(5,1)
v tíhovém poli (viz čl.4.2).
Potom na každý hmotný bod
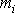 soustavy působí jeho tíha
soustavy působí jeho tíha
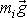 jakožto jediná vnější síla
jakožto jediná vnější síla
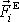 . Výsledná vnější síla působící na soustavu
. Výsledná vnější síla působící na soustavu
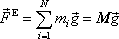 |
(5,105) |
je rovna tíze celé soustavy (M je celková hmotnost soustavy). Výsledný moment vnějších sil působících na soustavu
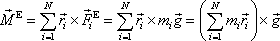 . . |
Výraz
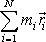 je však dle definice
(5,7)
hmotného středu soustavy roven
je však dle definice
(5,7)
hmotného středu soustavy roven
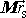 , a tedy
, a tedy
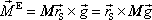 . . |
(5,106) |
Výsledný moment tíhových sil působících na soustavu hmotných
bodů (těleso) je roven momentu tíhy
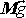 celé soustavy (tělesa), předpokládáme-li, že
tíha se nachází v hmotném středu soustavy. Soustavu sil působící na tuhé
těleso v tíhovém poli lze tedy nahradit jedinou silou tíhou tělesa
umístěnou v hmotném středu tělesa.
celé soustavy (tělesa), předpokládáme-li, že
tíha se nachází v hmotném středu soustavy. Soustavu sil působící na tuhé
těleso v tíhovém poli lze tedy nahradit jedinou silou tíhou tělesa
umístěnou v hmotném středu tělesa.
Hmotný střed bývá nazýván těžištěm, protože je působištěm síly, která na těleso působí v tíhovém poli.