 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Isolovanou nebo též uzavřenou soustavu hmotných bodů
nazýváme takovou soustavu, na jejíž hmotné body nepůsobí žádné vnější síly.
Jsou-li vnější síly
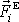působící na každý hmotný bod soustavy nulové, je dle
(5,32)
nulová výslednice
vnějších sil působících na soustavu a dle
(5,48)
je nulový i výsledný moment
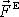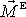vnějších sil působících na soustavu. Pro
isolovanou soustavu platí věta
(5,52)
o zachování hybnosti soustavy i věta
(5,61)
o zachování momentu hybnosti soustavy. Jelikož všechny síly
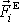v rovnici
(5,48)
jsou nulové, je výsledný moment
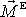vnějších sil působících na soustavu nulový, ať jsou hodnoty polohových vektorů
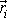jakékoliv. Pro isolovanou soustavu je výsledný moment
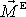nulový pro každou volbu bodu, vůči kterému
je počítán. Věta o zachování momentu hybnosti
(5,61)
se pak pro isolovanou
soustavu zjednoduší: Celkový moment hybnosti
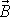isolované soustavy hmotných bodů je
s časem konstantní. Moment hybnosti zachovává v průběhu času svou
velikost, směr i smysl.
Zákon zachování hybnosti, zákonzachování momentu hybnosti a zákon zachování energie mají základní význam v celé fyzice. Jsou to zákony, které v případě, že jsou splněny podmínky jejich platnosti, udávají 7 mechanických veličin energii, 3 složky vektoru hybnosti a 3 složky vektoru momentu hybnosti, které v průběhu vyšetřovaného děje zůstávají konstantní. Tyto konstantní veličiny, které jsou funkcemi pouze času, souřadnic a rychlostí udávají prvé integrály (viz [14],str.50, [24], kap.17) pohybových rovnic a to takové prvé integrály,jejichž tvar lze určit fyzikálním rozborem řešeného problému.
Znalost prvých integrálůzjednodušuje řešení pohybových rovnic. Je-li počet stupňů volnosti vyšetřovaného systému malý, nebo v případech, kdy nepotřebujeme znát všechny údaje o vyšetřovaném ději, stačí často znalost zákonů zachování k úplnému řešení problémů. Řadu takto vyřešených příkladů lze najít např. v [20] a to především v kapitolách 3, 6 a 7. Určenírychlosti bloku rovnicí (5,58) může také sloužit jako příklad na užití zákona zachování hybnosti k řešení problému. Ve složitějších případech dochází k početnímu zjednodušení rovnic dávajících řešení vyšetřovaného problému. Rovnice odpovídající zákonům zachování obsahují nejvýše první derivace souřadnic (rychlosti), na rozdíl od původních pohybových rovnic, které obsahují druhé derivace souřadnic (zrychlení). Snížení řádu derivace je důvodem, proč zákony zachování označujeme jako prvé integrály pohybových rovnic.
S významem zákonů zachováníse podrobněji seznámíte v analytické mechanice (např. [11], [12]) a později se s nimi jako s výchozími principysetkáte i v dalších partiích teoretické fyziky.
Zákony zachování jsme již užiliv čl. 4.3 při řešení Keplerovy úlohy. Problém jsme pokládali za pohyb
jednoho bodu hmotnosti m
v silovém poli
(4,3)
. Počátek souřadnicové soustavy, tj. bod o polohovém vektoru
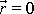, jsme umístili do hmotného bodu o hmotnosti M.
Takto zvolená soustava souřadná není inerciální a pro vyřešení pohybu bychom správně měli vedle pravé
síly gravitační uvažovat i síly zdánlivé . Abychom námi zvolenou soustavu
souřadnou mohli alespoň přibližně pokládat za inerciální, učinili jsme
předpoklad, že hmotnost M
je mnohokrát větší než hmotnost m; M>>m
. Pro Keplerovu úlohu je takový předpoklad oprávněný,protože hmotnost Slunce je mnohem větší než hmotnost
kterékoliv z planet a i než součet hmotností všech planet.
Dále je zvolený postup výhodný iz toho hlediska, že získané výsledky řešení můžeme aplikovat na kteroukoliv planetu a Keplerovy zákony vyslovit jako zákony platné pro celý planetární systém. Ve zvolené aproximaci se nám tak podaří vyřešit problém pohybu více těles, který je exaktně neřešitelný. Exaktně, tj. bez aproximací, lze řešit jen problém pohybu dvou těles, mezi kterými působí interaktivní síla. Jak lze postup použitý v čl. 4.3 upřesnit a v případě dvou těles libovolných hmotností aplikováním výsledků získaných v této kapitole exaktně vyřešit, ukážeme v následující stati.
V čl.4.3 jsme při řešeníKeplerovy úlohy vyšetřovali pohyb bodu hmotnosti m v gravitačním poli bodu o hmotnosti M, přičemž jsme předpokládali, že hmotnost M je natolik větší než hmotnost m, že takováto formulace problému je adekvátní.
Nyní nebudeme činit žádnépředpoklady o poměru hmotností obou hmotných bodů a problém vyřešíme přesně, bez aproximací. Dva hmotné body o hmotnostech m a M budeme pokládat za izolovanou soustavu. Předpokládáme tedy, že na body m a M nepůsobí vnější síly. Jedinou působící silou je mezi body působící gravitační síla (4,2)
 , |
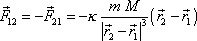(4,2) |
která je vnitřní silou soustavy.V rovnici
(4,2)
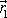je polohový vektor bodu o hmotnosti m a
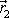polohový vektor bodu o hmotnosti M.
Dle věty
(5,59)
hmotný střed soustavy je buď v klidu nebo
v rovnoměrném přímočarém pohybu. Z různých inerciálních soustav
vybereme pro popis tu, v které hmotný střed soustavy je v klidu.
V ní zákon zachování hybnosti dává pro naši soustavu rovnici
 |
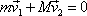(5,76) |
a zákon zachování momentu hybnostirovnici
 . |
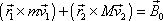(5,77) |
Jelikož síla (4,2) jekonzervativní, jsou splněny podmínky pro platnost zákona zachování mechanické energie a můžeme jej zapsat v tvaru
 . |
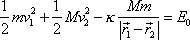(5,78) |
Poslední člen levé strany rovnice
(5,78)
je potenciální energie
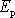odpovídající síle
(4,2)
. Je to veličina
závislá pouze na vzdálenosti hmotných bodů m a M.
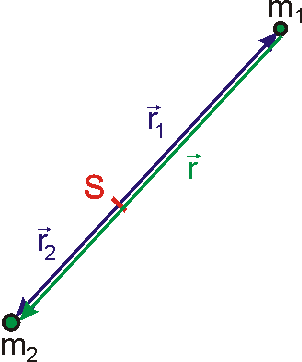
Hmotný střed soustavy je zapředpokladu
velmi blízko bodu o hmotnosti M.
Počátek soustavy souřadné položíme do hmotného středu S soustavy hmotných bodů
(viz obr.46). Potom z obecného výrazu
(5,7)
pro polohový vektor hmotného
středu v případě
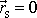dostáváme
 . |
(5,79) |
Vektory
a
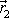jsou rovnoběžné a
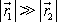. Z rovnice
(5,76)
plyne, že hybnosti
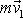a
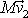jsou stejně velké a rovnoběžné. Úhly mezi vektory
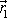a
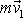a mezi vektory
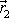a
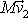na obr.46 označené
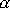jsou stejné. Z uvedených skutečností
plyne, že absolutní hodnota prvého členu na levé straně rovnice
(5,77)
je
podstatně větší než absolutní hodnota druhého členu
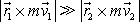. Je-li dle
(5,77)
konstantní hodnota součtu
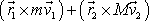, bude pak v dobrém přiblížení konstantní i hodnota
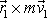, jak jsme předpokládali v rovnici
(4,25)
. Z rovnice
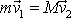při
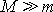plyne
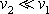, a tedy též
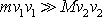. Člen
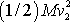v rovnici
(5,78)
lze zanedbat oproti členu
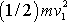, a tím rovnice
(5,78)
přechází na rovnici
(4,33)
. Právě provedenými úvahami jsme
ospravedlnili přibližnou správnost všech výchozích rovnic, které jsme při
řešení Keplerova problému užívali v čl.4.3.
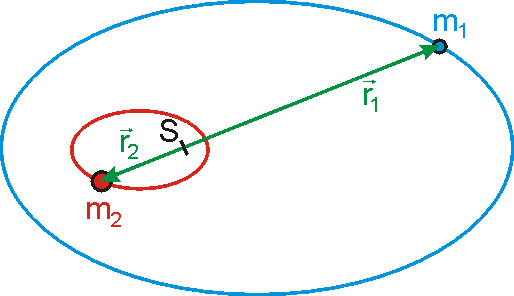
Ukážeme dále, jak lze pohyb izolované soustavy dvou hmotných bodů,budeme je nyní označovat
a
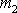, převést na řešení pohybu jednoho bodu v centrálním silovém poli. Počátek
souřadné soustavy položíme do hmotného středu
S soustavy. Potom dle
(5,79)
dostáváme mezi polohovými vektory
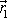hmotného bodu
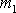a
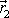hmotného bodu
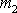vztah
 . |
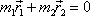(5,80) |
Zavedemevektor
 . |
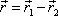(5,81) |
Je to vektor, jehož počátek ležív bodě
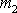a konec v bodě
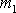. Vzhledem k speciální volbě počátku soustavy souřadné v hmotném středu
soustavy bodů má vektor
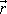stejný směr s vektory
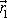a
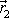(viz obr.47). Z rovnic
(5,80)
a
(5,81)
plyne vyjádření vektorů
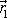a
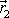pomocí vektoru
;
 . |
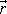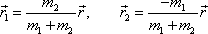(5,82) |
Pro rychlosti
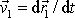a
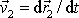z
(5,82)
plyne:
SETEQS2('knihI51do_soubory/eq0094M.gif','knihI51do_soubory/eq0095M.gif','(3,83)',',','.','2.26','.68');
kde
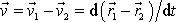. Předpokládáme-li, že mezi body soustavy působí pouze konzervativní síly, které
mají potenciální energii
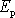, můžeme napsat rovnici vyjadřující zákon zachování mechanické energie soustavy
 . |
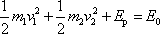(5,84) |
Dosadíme-liz
(5,83)
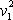za
a
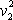do rovnice
(5,84)
, dostáváme po úpravě
 . |
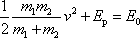(5,85) |
Zákonzachování momentu hybnosti (5,77) pro nyní užívané označení je dán rovnicí
 . |
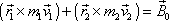(5,77) |
Zavedeme-lido rovnice
(5,77)
vyjádření
,
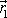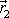dle
(5,82)
a
,
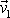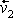dle
(5,83)
, můžeme ji postupně upravovat
 . |
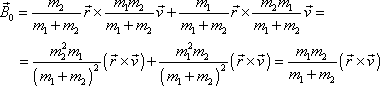Výsledekúpravy můžeme také zapsat v tvaru
 . |
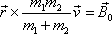(5,86) |
Dosadíme-lido rovnice
(5,85)
za
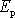potenciální energii vzájemného gravitačního působení bodů o hmotnostech
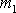a
 , |
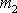
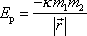(5,87) |
liší serovnice
(5,85)
a
(5,86)
od rovnic
(4,33)
a
(4,25)
, z kterých jsme
vycházeli v čl.4.3 při řešení Keplerova problému, pouze tím, že u rychlosti v
a u jejího čtverce
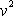v nich místo hmotnosti m obíhající částice vystupuje výraz
 , |
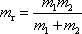(5,88) |
kterýnazveme redukovanou hmotností soustavy hmotných bodů
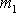a
.
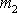Rovnice
(5,85)
a
(5,86)
se řešíformálně stejným způsobem jako rovnice řešené v čl.4.3. Výsledkem je
nalezení funkce
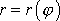, která má tvar polární rovnice kuželoseček. Z nalezené závislosti
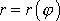určíme dráhy
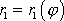a
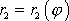hmotných bodů
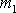a
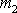dle rovnic plynoucích pro absolutní hodnoty vektorů z rovnic
(5,82)
. Je-li
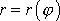rovnicí kuželosečky, jsou zřejmě
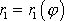a
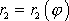rovnicemi podobných kuželoseček. Mezi vektory
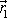a
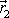platí rovnice
(5,80)
, z které plyne, že rozměry kuželoseček, po kterých se pohybují hmotné body
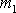a
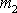, jsou v poměru
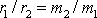. Dvě takové eliptické dráhy jsou znázorněny na obr.48.
V článku 4.3 jsme užívalioznačení
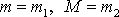a předpokládali jsme
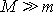. Potom pro redukovanou hmotnost
(5,88)
platí přibližné vyjádření
 . |
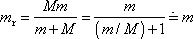Je-li
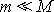, je
.
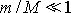Obdobně, užijeme-li rovnici
(5,82)
, dostaneme přibližné vyjádření pro vektor
,
 . |
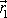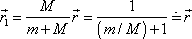Nemusíme-lirozlišovat mezi vektory
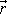a
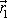a mezi redukovanou hmotností
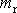a skutečnou hmotností oběžnice m,
řešení Keplerova problému podané v čl.4.3 je správné. Znovu zde na základě
přesného rozboru problému vidíme, že podmínka
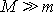je dosta-tečná pro to, aby řešení Keplerova
problému podané v čl.4.3 ve velmi dobrém přiblížení odpovídalo skutečnosti.
Ukázalijsme, že problém pohybu izolované soustavy dvou těles (přesně hmotných bodů)
lze převést na řešení pohybu jednoho hmotného bodu v známém silovém poli,
které je udáno svou potenciální energií
.
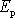Kromě gravitačního potenciálu
(5,87)
lze problém řešit i pro jiné tvary
potenciální energie, jak je ukázáno např. v [11], [12].
Máme-liizolovanou soustavu hmotných bodů, není možné, aby posunutím nebo rotací soustavy jako celku v prostoru byla na soustavu vykonána práce.
Uvažujmeelementární posuvný pohyb (translaci) izolované soustavy hmotných bodů
(5,1)
,
tj. pohyb, při kterém se každý hmotný bod soustavy posune o stejný vektor
.
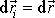Protože soustava je izolovaná, musí být vykonaná práce nulová:
 . |
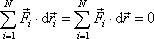(5,88) |
Posunutí
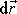je libovolné, a proto rovnici
(5,88)
lze splnit jen, když
 . |
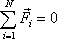(5,89) |
Síla
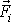působící na i-tý hmotný bod je rovna změně
hybnosti i-tého hmotného bodu;
 . |
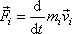Z rovnice (5,89) tedy plyne
 . |
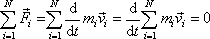(5,90) |
Derivacecelkové hybnosti soustavy
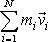je nulová, a tedy celková hybnost soustavy je konstantní;
 . |
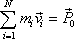(5,91) |
Předpokládáme-li,že práce
(5,88)
vykonaná při elementárním posunutí (translaci) izolované
soustavy hmotných bodů jako celku (všechna
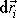stejná) je rovna nule, zjistíme, že musí být
splněna rovnice
(5,91)
zákon zachování hybnosti. Získaný výsledek bývá
formulován tak, že věta o zachování hybnosti je důsledkem homogenity prostoru.
Homogenitou se rozumí neměnnost vlastností při posunutí.
Spočítáme nyní práci vykonanou na
soustavu, která jako celek vykoná elementární rotaci. Při rotaci s úhlovou rychlostí
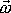se za čas dt posune každý bod soustavy o úsek dráhy
 . |
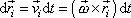Elementární práci
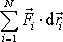můžeme pak při rotaci vyjádřit jako
 . |
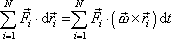(5,92) |
Pro izolovanou soustavu musí být elementární práce nulová, tedy
 . |
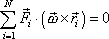(5,93) |
Do rovnice
(5,93)
dosadíme
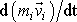za
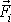a provedeme úpravu dle vzorce
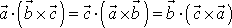, dostaneme
 , |
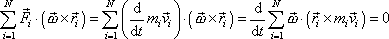odkud plyne
 . |
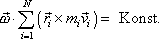(5,94) |
Z rovnice
(5,94)
plyne, že
průmět vektoru
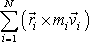do směru
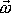je konstantní, tedy s časem stálý. Jelikož však vektor
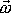je volen libovolně, je průmět vektoru
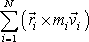do libovolného směru, a tedy i vektor sám s časem konstantní;
 . |
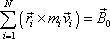(5,95) |
Vektor
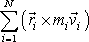je celkový moment hybnosti
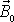soustavy a rovnice
(5,95)
říká ve shodě s
větou o zachování momentu hybnosti soustavy, že tento moment je konstantní.
Analogicky jako v případě posuvného pohybu soustavy, můžeme právě
provedený výpočet interpretovat tak, že věta o zachování momentu hybnosti
izolované soustavy hmotných bodů je důsledkem izotropie prostoru.
Izotropií se rozumí nezávislost vlastností na otočení, tedy na směru pozorování.
V teoretické mechanice odvodíte zákon zachování hybnosti a zákon zachování momentu hybnosti izolované soustavy hmotných bodů jako důsledek nezávislosti chování soustavy na posuvu a otočení souřadnicové soustavy, kterou použijete k popisu soustavy hmotných bodů. Ukážete si též, že zákon zachování mechanické energie lze odvodit jako důsledek libovůle ve volbě počátečního okamžiku (translace v čase), od kterého se počítají děje probíhající v soustavě (viz např. [11], [12]).
|
|
|
|
|
|
|
|
|