---

---

5.5 Energie soustavy hmotnýchbodů

Kinetickou energií soustavyhmotných bodů rozumíme součet

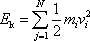(5,62)

kinetických energií jednotlivýchbodů soustavy. Stejně jako v rovnici (5,23) označíme 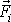sílu působící na i-tý hmotný bod. Přejdou-li body soustavy z jedné polohy označíme ji I do druhé polohy, kterou označíme II, síly 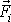vykonají na hmotné body soustavy práci, jejíž celková hodnota

.

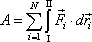(5,63)

Integrál 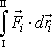(přes i se nesčítá) značí práci vykonanou na i-tý hmotný bod, přejde-li ze své původní polohy označíme ji 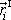do konečné polohy 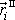. Tato práce je dle (3,11) rovna přírůstku kinetické energie i-tého hmotného bodu,

.

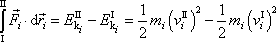(5,64)

V rovnici (5,64) 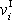značí velikost rychlosti i-tého hmotného bodu v poloze I, 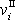velikost rychlosti i-tého hmotného bodu v poloze II. Dosadíme-li vyjádření integrálu (5,64) do rovnice (5,63) , dostáváme

,

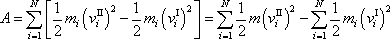což můžeme s přihlédnutím k (5,62) stručně zapsat jako

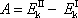(5,65)

a formulovat větu o kinetické energii soustavy: Práce A vykonaná vnějšími i vnitřními silami na soustavu hmotných bodů, přejde-li z polohy I do polohy II, je rovna přírůstku kinetické energie soustavy, tj. rozdílu 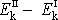mezi kinetickou energií soustavy v poloze II a kinetickou energií soustavy v poloze I.

Zdůrazňujeme,že změny kinetické energie ovlivňují jak vnější tak i vnitřní síly. Síla 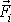uvažovaná při odvozování věty (5,65) je dle (5,24) součtem výslednice vnějších a vnitřních sil působících na i-tý hmotný bod soustavy. Vnitřní síly ovlivňují změny kinetické energie jen u volné soustavy hmotných bodů. V tuhé soustavě hmotných bodů nebo v tuhém tělese vnitřní síly vzhledem k pevným vzdálenostem mezi body těchto systémů práci nekonají. Volná soustava může měnit svou kinetickou energii, i když na soustavu žádné vnější síly nepůsobí.

Jsou-li vnější i vnitřní sílypůsobící na soustavu konzervativní, je práci A vykonanou na systém možno vyjádřit jako úbytek potenciální energie 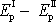soustavy, přejde-li soustava z polohy I do polohy II;

.

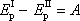(5,66)

Porovnáním rovnic (5,65) a (5,66) dostáváme zákon zachování mechanické energie

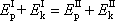(5,67)

pro soustavu hmotných bodů, nakterou působí pouze konzervativní síly. Je-li některá z působících sil, ať vnější nebo vnitřní, disipativní, zákon zachování mechanické energie (5,67) pro takovou soustavu neplatí. V soustavě hmotných bodů může také probíhat děj (např. výbuch), jehož působením se celková mechanická energie systému zvýší, potom také rovnice (5,67) neplatí. Ani nepřítomnost vnějších sil působících na soustavu nezaručí platnost rovnice (5,67) , jsou-li vnitřní síly nekonzervativní.

Uvedeme ještě zjednodušené zněnírovnic (5,65) a (5,67) pro tuhou soustavu hmotných bodů a pro tuhé těleso, v kterých práce vnitřních sil je nulová. Rovnici (5,65) lze pak interpretovat takto:

Zákon zachování mechanické energie (5,67) lze pro tuhé těleso (tuhou soustavu) vyslovit takto:

Kinetickouenergii 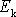soustavy hmotných bodů danou rovnicí (5,62) rozložíme na dva členy. Rychlost 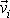i-tého hmotného bodu soustavy budeme pokládat za součet rychlosti hmotného středu soustavy 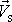a rychlosti 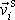i-tého bodu vůči hmotnému středu

.

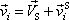(5,68)

Pro tuhé těleso odpovídá rozklad (5,68) rozkladu (5,16) , je-li za bod, který má rychlost 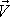volen hmotný střed a není-li rychlost 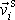, která v případě tuhého tělesa je pouze rotační rychlostí, rozepsána jako

.

(5,69)

V rovnici (5,69) je 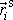značen polohový vektor i-tého hmotného bodu vůči hmotnému středu tělesa. Dosadíme vyjádření (5,68) do rovnice (5,62) , dostaneme

.

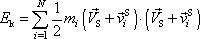(5,70)

Skalární součin

,

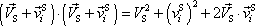(5,71)

a tedy

.

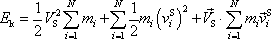(5,72)

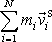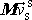Výraz je celková hybnost soustavy vůči jejímu hmotnému středu. Postupem užitým při úpravě rovnice (5,32) na tvar (5,35) lze výraz přepsat na tvar , kde M je celková hmotnost soustavy a 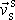rychlost hmotného středu soustavy vůči hmotnému středu soustavy. Veličina 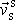je zřejmě nulová, a tedy i

.

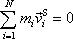(5,73)

Pro celkovou kinetickou energii soustavy hmotných bodů tak dostáváme vyjádření, které bývá označováno jako Königova věta:

.

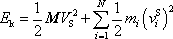(5,74)

Kinetická energie 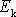se skládá z výrazu 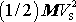, což je kinetická energie bodu o hmotnosti rovné celkové hmotnosti soustavy M, který má rychlost 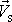hmotného středu soustavy, a z kinetické energie 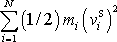pohybu hmotných bodů soustavy vůči jejímu hmotnému středu.

Člen

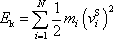(5,75)

bývá nazýván vnitřní kinetickáenergie soustavy. Königova věta je tedy větouo rozkladu kinetické energie soustavy na vnitřní kinetickou energii soustavy a člen 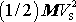, který představuje kinetickou energii hmotného středu soustavy, myslíme-li si v něm soustředěnu veškerou hmotnost soustavy.

---

---