Uvažujme nyní soustavu hmotných bodů (5,1) , pro kterou výslednice vnějších sil působících na soustavu
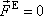 . . |
(5,51) |
Z věty o hybnosti
(5,33)
pro takovou soustavu plyne
 , a tudíž
, a tudíž
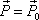 , , |
(5,52) |
kde
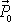 je konstantní vektor.
je konstantní vektor.
Celková hybnost
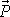 soustavy hmotných bodů zachovává
v průběhu času svou velikost, směr a smysl, když výslednice vnějších sil
působících na soustavu je nulová. Vyslovená věta se nazývá
věta o zachování hybnosti soustavy
a platí zřejmě pouze v případě, když
výslednice vnějších sil působících na soustavu je nulová;
soustavy hmotných bodů zachovává
v průběhu času svou velikost, směr a smysl, když výslednice vnějších sil
působících na soustavu je nulová. Vyslovená věta se nazývá
věta o zachování hybnosti soustavy
a platí zřejmě pouze v případě, když
výslednice vnějších sil působících na soustavu je nulová;
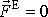 .
.
Tato věta je z elementárního výkladu známá pro případ dvou hmotných bodů, na které nepůsobí vnější síly. Užívá se pro ni název zákon zachování hybnosti. Rozepsáním rovnice (5,52) pro dva body dostáváme
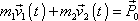 , , |
(5,53) |
kde
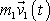 je s časem t proměnná hybnost
je s časem t proměnná hybnost
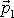 prvého hmotného bodu a
prvého hmotného bodu a
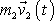 s časem t proměnná hybnost
s časem t proměnná hybnost
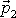 druhého hmotného bodu.
druhého hmotného bodu.
Nejčastěji se rovnice
(5,53)
užívá k vyšetřování případů, kdy v nějakém časovém
intervalu dochází k interakci mezi hmotnými body a mimo tento interval
vzájemné působení hmotných bodů je zanedbatelné. V době před časovým
intervalem, v kterém dochází k interakci, jsou pak rychlosti
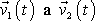 prakticky konstantní a zavedeme pro ně
označení
prakticky konstantní a zavedeme pro ně
označení
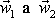 . Rychlosti hmotných bodů po interakci označíme
. Rychlosti hmotných bodů po interakci označíme
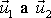 . Protože dle
(5,53)
. Protože dle
(5,53)
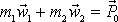 a stejnému konstantnímu vektoru
a stejnému konstantnímu vektoru
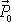 je roven i výraz
je roven i výraz
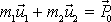 , dostáváme
, dostáváme
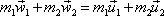 . . |
(5,54) |
V elementárním
výkladu zvláštní pozornost je věnována případu, kdy před interakcí jsou oba
hmotné body v klidu, tedy
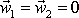 , a tudíž i
, a tudíž i
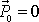 . Potom pro rychlosti
. Potom pro rychlosti
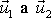 z rovnice
(5,54)
plyne
z rovnice
(5,54)
plyne
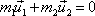 , , |
tedy
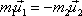 . . |
(5,55) |
Dva hmotné body, jež jsou původně v klidu, se po interakci rozletí stejným směrem v opačném smyslu a velikost jejich rychlosti je v opačném poměru než velikost jejich hmotností.
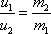 . . |
(5,56) |
Z rovnice
(5,55)
plyne totiž pro velikosti vektorů rovnice
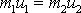 a z té pak již zřejmým způsobem rovnice
(5,56)
. Lze udat řadu příkladů ilustrujících právě probraný případ:
a z té pak již zřejmým způsobem rovnice
(5,56)
. Lze udat řadu příkladů ilustrujících právě probraný případ:
Stojím-li na vozíku, který je v klidu a posléze z něj vyskočím, rozjede se vozík na opačnou stranu, než na kterou jsem vyskočil. Velikost mé rychlosti k rychlosti vozíku je v opačném poměru než velikost mé hmotnosti k hmotnosti vozíku. Při stejném impulsu síly, který vynaložím na své rozběhnutí, dosáhnu tím větší rychlosti vůči podlaze, na kterou skočím, čím větší bude hmotnost vozíku.
Při výstřelu z pušky střela o hmotnosti
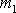 se pohybuje rychlostí
se pohybuje rychlostí
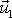 . Dle rovnice
(5,55)
by se puška měla pohybovat rychlostí
. Dle rovnice
(5,55)
by se puška měla pohybovat rychlostí
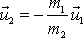 , kde
, kde
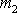 je hmotnost pušky. Puška se skutečně po
výstřelu hodlá pohybovat udanou rychlostí proti smyslu výstřelu, je však držena
střelcem, který tento pohyb zmaří za cenu nepříjemného úderu do ramene, známého
pod názvem zpětný náraz. Podobně při výstřelu z děla hlaveň koná zpětný
pohyb (zákluz), který je na určité dráze brzděn a přenášen na podvozek (lafetu)
děla. Kromě právě uvedených existují i zbraně odlišné konstrukce, tzv.
bezzákluzové. U těchto zbraní je hlaveň na obou koncích otevřená a střela získá
svou hybnost na úkor plynů spálených při výstřelu, které se stejně velkou
hybností jako střela opustí hlaveň opačným směrem. Podobný princip je užíván i
při pohonu raket, kde však na rozdíl od bezzákluzových zbraní vypouštění
spáleného paliva zvyšující hybnost rakety probíhá po delší dobu. Raketový pohyb
bude rozebrán v článku 7.4.
je hmotnost pušky. Puška se skutečně po
výstřelu hodlá pohybovat udanou rychlostí proti smyslu výstřelu, je však držena
střelcem, který tento pohyb zmaří za cenu nepříjemného úderu do ramene, známého
pod názvem zpětný náraz. Podobně při výstřelu z děla hlaveň koná zpětný
pohyb (zákluz), který je na určité dráze brzděn a přenášen na podvozek (lafetu)
děla. Kromě právě uvedených existují i zbraně odlišné konstrukce, tzv.
bezzákluzové. U těchto zbraní je hlaveň na obou koncích otevřená a střela získá
svou hybnost na úkor plynů spálených při výstřelu, které se stejně velkou
hybností jako střela opustí hlaveň opačným směrem. Podobný princip je užíván i
při pohonu raket, kde však na rozdíl od bezzákluzových zbraní vypouštění
spáleného paliva zvyšující hybnost rakety probíhá po delší dobu. Raketový pohyb
bude rozebrán v článku 7.4.
Kromě případu, kdy na začátku děje jsou oba hmotné body v klidu, je často také
elementárně sledován případ, kdy jeden např. první hmotný bod je před
interakcí v klidu a druhý se pohybuje rychlostí
 a po interakci se oba body spojí. Z rovnice
(5,54)
dostáváme pro tento případ rovnici
a po interakci se oba body spojí. Z rovnice
(5,54)
dostáváme pro tento případ rovnici
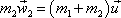 , , |
(5,57) |
kde společnou rychlost obou hmotných bodů po interakci jsme označili
 . V uvažovaném případě se po interakci oba hmotné body pohybují stejným směrem
i smyslem jako hmotný bod před interakcí, přičemž, jak plyne z rovnice
(5,57)
, velikost společné rychlosti
. V uvažovaném případě se po interakci oba hmotné body pohybují stejným směrem
i smyslem jako hmotný bod před interakcí, přičemž, jak plyne z rovnice
(5,57)
, velikost společné rychlosti
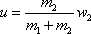 . . |
(5,58) |
Zasáhne-li
střela dřevěný blok, který do zásahu byl v klidu, a uvízne v něm, lze
dle vzorce
(5,58)
vypočítat rychlost bloku poté, kdy v něm střela uvízla.
Musíme ovšem znát hmotnost a rychlost střely i hmotnost bloku a zanedbat vnější
síly působící na blok. Zpravidla se zanedbání vnějších sil působících na blok
vztahuje pouze na dobu, po kterou se střela v bloku brzdí a rychlost
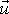 se pokládá za počáteční rychlost pohybu
bloku po zásahu střelou. Většinou při sledovaném ději nebývá počítána
rychlost
se pokládá za počáteční rychlost pohybu
bloku po zásahu střelou. Většinou při sledovaném ději nebývá počítána
rychlost
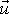 , ale rychlost střely
, ale rychlost střely
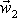 (viz např. [20] , kap.6, [17], čl.
2.2.1.2). Často bývá blok, do kterého se střílí zavěšen tak, že tvoří kyvadlo.
Zařízení se nazývá balistické kyvadlo
a rychlost střely se určuje z maximální výchylky (amplitudy kyvu), kterou
kyvadlo po zásahu střelou dosáhne. Kyvadlo se pohybuje podstatně pomaleji než
střela a výchylka se dá snadno změřit. V analogii s balistickým
kyvadlem se nazývají balistické i další metody užívané v měrné fyzice, při
nichž se rychle probíhající děje transformují na pomalejší snadněji měřitelné
děje.
(viz např. [20] , kap.6, [17], čl.
2.2.1.2). Často bývá blok, do kterého se střílí zavěšen tak, že tvoří kyvadlo.
Zařízení se nazývá balistické kyvadlo
a rychlost střely se určuje z maximální výchylky (amplitudy kyvu), kterou
kyvadlo po zásahu střelou dosáhne. Kyvadlo se pohybuje podstatně pomaleji než
střela a výchylka se dá snadno změřit. V analogii s balistickým
kyvadlem se nazývají balistické i další metody užívané v měrné fyzice, při
nichž se rychle probíhající děje transformují na pomalejší snadněji měřitelné
děje.
V obecném případě, kdy se dva hmotné body před interakcí i po ní pohybují samostatně, nestačí rovnice (5,54) na úplné řešení problému. Některé závěry týkající se tohoto obecného případu probereme v článku 7.1.
Z rovnice
(5,35)
pro soustavu hmotných bodů, pro kterou výslednice
 vnějších sil působících na soustavu je nulová, plyne
vnějších sil působících na soustavu je nulová, plyne
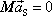 , , |
(5,59) |
a tedy hmotný střed takové soustavy má nulové zrychlení
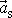 . Formulujeme tedy pro tento případ následující závěr:
. Formulujeme tedy pro tento případ následující závěr:
Působí-li na soustavu hmotných bodů nulová výsledná vnější síla
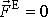 , je hmotný střed soustavy v klidu nebo koná rovnoměrný přímočarý pohyb. O
tom, který z obou pohybů nastane, rozhodují počáteční podmínky pohybu
soustavy.
, je hmotný střed soustavy v klidu nebo koná rovnoměrný přímočarý pohyb. O
tom, který z obou pohybů nastane, rozhodují počáteční podmínky pohybu
soustavy.
Mějme soustavu hmotných bodů (5,1) , pro které vzhledem k nějakému bodu A výsledný moment vnějších sil působících na soustavu je nulový,
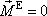 . . |
(5,60) |
Potom dle rovnice
(5,49)
 a celkový moment hybnosti soustavy vzhledem k bodu A je konstantní,
a celkový moment hybnosti soustavy vzhledem k bodu A je konstantní,
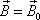 . . |
(5,61) |
V rovnici
(5,61)
je
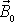 označen konstantní vektor. Závěr můžeme formulovat jako
větu o zachování momentu hybnosti soustavy:
označen konstantní vektor. Závěr můžeme formulovat jako
větu o zachování momentu hybnosti soustavy:
Je-li vůči některému bodu výsledný moment vnějších sil působících na soustavu po jistou dobu nulový, potom po tuto dobu je celkový moment hybnosti soustavy vzhledem k uvažovanému bodu konstantní.
Konkrétní důsledky plynoucí z této věty pro otáčení tuhého tělesa kolem pevné osy probereme v čl. 6.1 a pro případ rotace kolem bodu v čl. 6.5.