 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Mějme soustavu N hmotných bodů zadanou údaji
(5,1)
. Na i-tý hmotný bod působí síla
a platí pro něj podle druhého Newtonova zákona
(2,1)
rovnice
 . |
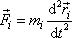(5,23) |
Sílu
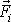můžeme rozložit na dvě části: na výslednici sil, kterými na i-tý hmotný bod
působí ostatní hmotné body soustavy označíme ji
a na výslednici
sil, kterými na i-tý hmotný bod působí hmotné body a
jiné objekty, které nepatří do uvažované soustavy hmotných bodů. Síly,
z kterých je složena síla
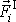nazýváme vnitřními (interními) silami
soustavy a síly, z kterých je složena
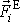nazýváme vnějšími (externími) silami působícími na soustavu. Síla
je výslednice vnitřních sil a
výslednice vnějších sil působících na i-tý hmotný bod soustavy. Síla
z rovnice
(5,23)
je rovna jejich vektorovému součtu,
 . |
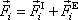(5,24) |
Na následující stránce je na obr.44 znázorněna soustava sestávající se ze tří
hmotných bodů
. Pružina mezi prvním a druhým bodem znázorňuje pružnou vazbu, pokládáme-li ji za
nehmotnou. Při protažení pružiny se body přitahují, jak je naznačeno na
obrázku; při stlačení pružiny se body odpuzují. Síly, kterými pružina působí na
1. a 2. hmotný bod jsou vnitřními silami soustavy. Předpoklá-dejme, že celá
soustava se nachází v tíhovém poli. Tíhy hmotných bodů
jsou vnějšími silami působícími na soustavu. Kdybychom
však Zemi zahrnuli jako čtvrtý bod do
uvažované soustavy, staly by se tíhy vnitřními silami soustavy.
Rozdělení sil na vnější a vnitřní zřejmě závisí na tom, které prvky do soustavy zahrneme. Máme-li soustavu elektricky nabitých částic, jsou coulombovské síly mezi nimi působící vnitřními silami soustavy. Vložíme-li soustavu do vnějšího elektrického pole, budou síly působící na částice od tohoto pole vnějšími silami. Zahrneme-li však do soustavy i zdroje elektrického pole, budou obojí výše uvažované síly vnitřními silami soustavy.
Výslednici
vnitřních sil působících na i
-tý hmotný bod soustavy lze psát jako součet
 . |
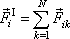(5,25) |
kde symbol
značí sílu působící od k-tého na i-tý
hmotný bod soustavy. Sílu, kterou působí bod sám na sebe je zřejmě nutné
pokládat za nulovou, tedy v dané symbolice
.
Zavedeme-li do rovnice (5,23) vyjádření (5,24) a (5,25) , dostáváme
 . |
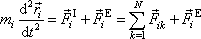(5,26) |
Sečteme-li rovnice (5,26) platné pro jednotlivé body soustavy, dostaneme
 . |
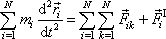(5,27) |
Rozepíšeme výraz
, platí
 . |
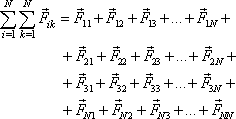Kromě výrazů se stejnými indexy
, které jsou nulové, se celý součet rozpadne na součty
dvou sil symetricky rozložených kolem diagonály
tvořené výrazy se stejnými indexy. Síla
, kterou k-tý bod působí na i-tý bod a síla
, kterou i-tý bod působí na k-tý, jsou dle Newtonova zákona akce a
reakce (třetí zákon) stejně velké, stejného směru, ale opačného smyslu:
 . |
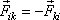(5,28) |
Každá dvojice
dá nulový příspěvek do dvojitého součtu
, a tedy
 . |
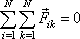(5,29) |
Uvědomíme-li si, že hmotnost
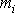každého bodu je konstantní a součet derivací je roven derivaci součtu, můžeme na levé straně rovnice
(5,27)
místo
psát
. Vzhledem k tomu, že platí
(5,29)
, dostáváme tak z
(5,27)
rovnici
 . |
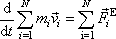(5,30) |
Výraz
jakožto součin hmotnosti
a rychlosti
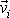i-tého hmotného bodu soustavy je hybností
tohoto bodu. Součet
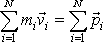je součtem hybností hmotných bodů soustavy. Zavedeme pro něj označení
 |
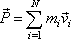(5,31) |
a nazveme jej celkovou hybností soustavy.
Výraz
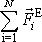znamená součet všech výslednic vnějších sil
působících na jednotlivé body soustavy. Zavedeme pro něj označení
 |
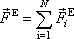(5,32) |
a nazveme jej výslednicí vnějších sil působících na soustavu. S označeními (5,31) a (5,32) lze rovnici (5,30) stručně zapsat
 . |
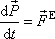(5,33) |
Poslední rovnice bývá označována jako věta o hybnosti soustavy nebo též první impulsová věta. Uvedeme její slovní formulaci: Časová derivace celkové hybnosti soustavy je rovna výslednici vnějších sil působících na soustavu.
Rovnici
(5,33)
lze též upravit na tvar dávající pohybovou
rovnici hmotného středu soustavy. Hmotný střed soustavy je definován rovnicí
(5,7)
. Pohybují-li se hmotné středy soustavy, jsou jak polohové vektory
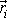jednotlivých jejích bodů, tak polohový vektor
hmotného středu funkcemi času. Časová závislost
udává trajektorii hmotného středu soustavy, výraz
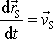udává rychlost a
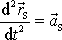zrychlení hmotného středu soustavy. Definiční rovnici
(5,7)
hmotného středu soustavy hmotných bodů vynásobenou
celkovou hmotností M soustavy
 |
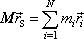derivujeme dle času t, dostáváme
 . |
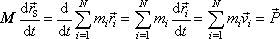(5,34) |
Dle
(5,34)
dosadíme
za hybnost soustavy
do rovnice
(5,33)
.a její levou stranu upravíme:
 . |
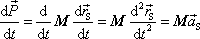Místo rovnice (5,33) tak dostaneme rovnici:
 . |
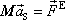(5,35) |
Obsah poslední rovnice bývá označován jako
věta o pohybu hmotného středu soustavy.
Slovní formulace vyplývá z analogie mezi rovnicí
(5,35)
a pohybovou
rovnicí hmotného bodu
(2,1)
: Hmotný střed soustavy se pohybuje jako hmotný bod,
který má hmotnost rovnou celkové hmotnosti M soustavy a na nějž
působí výslednice vnějších sil
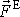působících na soustavu.
Rovnice
(5,35)
je tedy pohybovou rovnicí jednoho, rozložením hmotných bodů pevně
určeného, bodu soustavy hmotného středu. Výhodná je formální shodnost rovnice
(5,35)
s rovnicí
(2,1)
. Zjistíme-li výslednici
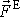vnějších sil působících na soustavu, můžeme
metodami podrobněji popsanými v článku 2.3 hledat trajektorii hmotného
středu soustavy. Pohyb hmotného středu soustavy, a tedy též pohyb těžiště
tělesa, se vyšetřuje stejnými metodami jako pohyb hmotného bodu.
Nacházejí-li se např. všechny hmotné body soustavy
(5,1)
v tíhovém poli, působí na
každý hmotný bod vnější síla rovná tíze hmotného bodu
. Budeme předpokládat, že na soustavu žádné další síly kromě tíhových nepůsobí.
Potom výslednice vnějších sil působících na soustavu
 . |
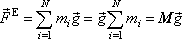(5,36) |
Rovnice
(5,35)
pro pohyb hmotného středu soustavy pro
dané rovnicí
(5,36)
má tvar
 , |
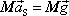(5,37) |
a je tedy formálně shodná s rovnicí (2,7) .
Řešení rovnice (5,37) je shodné s řešením rovnice (2,7) . Podle počátečních podmínek pohybu se hmotný střed soustavy, jejíž všechny body se nacházejí v tíhovém poli, a na které kromě tíhových jiné vnější síly nepůsobí, pohybuje po některé z parabolických nebo přímkových trajektorií určených rovnicemi (2,9) . Koná tedy některý z vrhů.
Rovnice (5,35) ospravedlňuje běžnou praxi, kdy výsledky získané pro pohyb hmotného bodu aplikujeme na pohyb těles. Nezajímá-li nás rotace tělesa a nehrají-li podstatnou roli konečné rozměry tělesa, je to možné.
Vyšetříme nyní, jaký vliv na pohyb soustavy mají momenty sil působící na jednotlivé její hmotné body. Vyjdeme z rovnice (3,36)
 , |
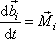(3,36) |
která platí pro (libovolný) i-tý hmotný bod soustavy. Zvolíme-li
počátek soustavy souřadné za bod, vůči kterému počítáme moment hybnosti i-tého
hmotného bodu a moment síly
působící na i-tý hmotný bod, můžeme rovnici
(3,36)
rozepsat na tvar
 . |
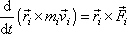(5,38) |
V rovnici
(5,38)
je
polohový vektor,
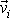rychlost a
hmotnost i-tého bodu soustavy. Sílu
působící na i-tý hmotný bod soustavy
rozložíme dle
(5,24)
na výslednici vnitřních sil
a výslednici vnějších sil
působících na i-tý bod soustavy;
. Rovnice
(5,38)
platné pro jednotlivé body sečteme přes všechny body soustavy, dostaneme:
 . |
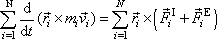(5,39) |
Užijeme-li pravidla o součtu derivací a distributivnosti vektorového součinu, můžeme přepsat rovnici (5,39) na tvar
 . |
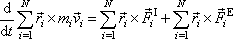(5,40) |
Dosadíme za
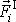dle
(5,25)
a výraz
přepíšeme na tvar
.
Dle distributivního zákona pro vektorový součin platí
 . |
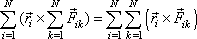(5,41) |
Jelikož pro
jsou
a vektorový součin s jedním nulovým
součinitelem je nulový, lze rozložit dvojitou sumu na pravé straně rovnice
(5,41)
na dvojice sčítanců
 , |
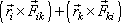(5,42) |
kde
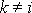. Mezi
platí vztah
(5,28)
, a tedy
 . |
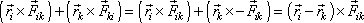(5,43) |
Je-li síla působící mezi i-tým a k-tým bodem centrální, je vektor
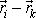rovnoběžný s vektorem
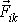a výraz
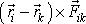je nulový (viz též obr.45). Potom je nulový
každý součet
(5,42)
, a tedy i celý dvojitý součet
(5,41)
 . |
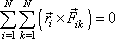(5,44) |
Rozložíme-li síly na síly působící mezi dvěma body, je předpoklad o jejich centrálnosti velmi obecný, a proto jej jako omezení platnosti dále odvozených vět nebudeme znovu zdůrazňovat.
Při důkazu tvrzení (5,44) můžeme též vyjít z rovnosti výrazů
 . |
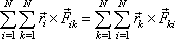Potom
 . |
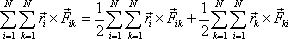Alejelikož též
 , |
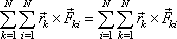je
 . |
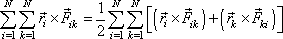(5,45) |
Za sumačním znamením na pravé straně rovnice
(5,45)
jsou součty tvaru
(5,42)
,
které pro
jsou nulové dle výše provedeného rozboru a pro
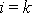jsou nulové, jelikož
pro
.
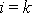Z rovnice (5,44) plyne, že je nulový prvý člen na pravé straně rovnice (5,40) , a tedy
 . |
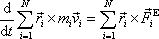(5,46) |
Výraz
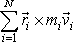je součtem momentů hybnosti
jednotlivých hmotných bodů soustavy vzhledem k počátku soustavy souřadné. Zavedeme pro něj označení
 |
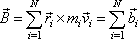(5,47) |
a název celkový moment hybnosti soustavy hmotných bodů.
Výraz na pravé straně rovnice
(5,46)
je součtem momentů
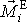výslednic vnějších sil
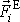působících na jednotlivé hmotné body
soustavy vůči počátku soustavy souřadné. Zavedeme pro něj označení
 |
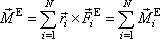(5,48) |
a název výsledný moment vnějších sil působících na soustavu hmotných bodů. Se zavedeným označením můžeme rovnici (5,46) zapsat stručně:
 . |
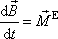(5,49) |
Poslední rovnice je obvykle užívaným zápisem věty o momentu hybnosti soustavy, která bývá též označována jako druhá věta impulsová. Uvedeme její slovní formulaci: Časová derivace celkového momentu hybnosti soustavy hmotných bodů je rovna výslednému momentu vnějších sil působících na soustavu. Podmínkou rovnosti je, že moment hybnosti a moment síly je počítán vzhledem k témuž bodu.
Větu o hybnosti soustavy
(5,33)
i větu o momentu hybnosti soustavy
(5,49)
jsme
odvodili pro libovolnou soustavu hmotných bodů. Věty tedy zřejmě platí pro
tuhou soustavu hmotných bodů a tím i pro tuhé těleso. Tuhé těleso, stejně jako
tuhá soustava hmotných bodů, má šest stupňů volnosti, jak jsme ukázali v článku
5.1.
Pro tuhé těleso jsou dvě vektorové rovnice
(5,33)
a
(5,49)
jeho pohybovými rovnicemi.
Šest skalárních rovnic, které tyto dvě vektorové rovnice
reprezentují, tvoří úplný systém rovnic pro určení šesti funkcí kinematicky
určujících pohyb tuhého tělesa. Za těchto šest funkcí volíme dvě vektorové
funkce
(5,22)
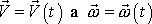. Úpravou věty o hybnosti soustavy pro stanovení funkce
je věta
(5,35)
o pohybu hmotného středu
soustavy. Při kinematických úvahách předcházejícího článku jsme bod tělesa na
obr.42 označený A, který se pohybuje rychlostí
a vůči němuž uvažujeme rotaci tělesa, volili
libovolně. Vybereme-li za tento bod hmotný střed (těžiště) tělesa, je rovnice
(5,35)
jeho pohybovou rovnicí. Rychlost
, jedná-li se o rychlost hmotného středu tělesa, označíme
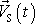a rovnici
(5,35)
zapíšeme ve tvaru
 . |
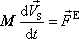(5,50) |
Známe-li výslednici
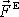vnějších sil působících na těleso, je
rovnice
(5,50)
pohybovou rovnicí hmotného středu tělesa, tj. soustavou
diferenciálních rovnic pro určení neznámé funkce
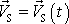. Podstatně obtížnější úpravou rovnice
(5,49)
na rovnici pro stanovení druhé
z funkcí
(5,22)
se budeme podrobněji zabývat v kapitole
6.
Některé další závěry plynoucí z rovnice (5,33) a (5,49) pro volné i tuhé soustavy hmotných bodů uvedeme v následujícím článku.
|
|
|
|
|
|
|
|
|