Kinematiku bodu jsme probrali v kapitole 1. Tam jsme
ukázali, že pohyb je určen, jsou-li dány tři parametrické rovnice
(1,2)
, tj.
rovnice udávající časovou závislost souřadnic
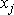 bodu. Tři parametrické rovnice odpovídají
třem stupňům volnosti hmotného bodu. Chceme-li popsat pohyb volné soustavy
hmotných bodů, musíme znát pohyb všech jejích bodů, tj. časový průběh
všech N polohových vektorů
bodu. Tři parametrické rovnice odpovídají
třem stupňům volnosti hmotného bodu. Chceme-li popsat pohyb volné soustavy
hmotných bodů, musíme znát pohyb všech jejích bodů, tj. časový průběh
všech N polohových vektorů
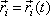 |
(5,11) |
popisujících dle (5,1) soustavu. Znát (5,11) znamená znát 3N funkcí parametrických rovnic
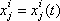 |
(i=1, 2, ,N; j= 1, 2, 3) udávajících časový průběh všech souřadnic všech bodů soustavy.
Tuhá soustava hmotných bodů a tuhé těleso mají pouze šest stupňů volnosti, jak bylo
ukázáno v předchozím článku. Jejich poloha je stanovena udáním šesti
souřadnic. Zjistíme-li časovou závislost šesti souřadnic, určíme tím pohyb
tuhého tělesa nebo tuhé soustavy hmotných bodů. Budeme hledat vhodnou volbu
těchto souřadnic. Myslitelné by bylo stanovit časovou závislost polohy tří bodů
užívaných k určení polohy tuhého tělesa v předcházejícím článku.
Znamenalo by to stanovit časovou závislost polohových vektorů
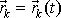 ,
,
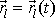 a
a
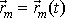 . Počet nezávisle volitelných funkcí by byl redukován z devíti na šest tím,
že by musely být dodrženy vztahy
(5,2)
, kde vzdálenosti
. Počet nezávisle volitelných funkcí by byl redukován z devíti na šest tím,
že by musely být dodrženy vztahy
(5,2)
, kde vzdálenosti
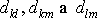 jsou s časem konstantní. Takový postup
se však pro jeho nepřehlednost zpravidla v kinematice tuhého tělesa neužívá.
jsou s časem konstantní. Takový postup
se však pro jeho nepřehlednost zpravidla v kinematice tuhého tělesa neužívá.
 Místo stanovení polohy tří pevných bodů v tělese, vázaných relacemi
(5,2)
lze
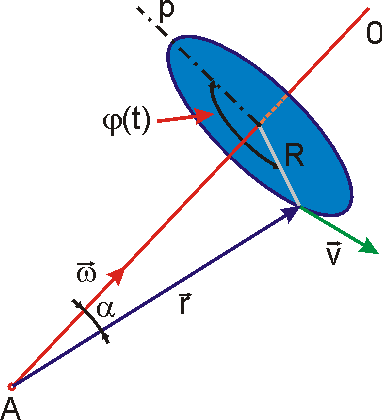
stanovit polohu tělesa v prostoru i jinými šesti údaji. Pro východisko
kinematických úvah je nejvhodnější, když stanovíme polohu jednoho bodu, tímto
bodem procházející osy a určíme natočení tělesa vůči této ose. Postup je
znázorněn na obr.39, kde bod je označen A, osa o
a natočení je charak-terizováno úhlem j
mezi přímkou pevnou v tělese značenou
plně a přímkou pevnou v prostoru značenou čárkovaně. Obě přímky tvořící
úhel j jsou kolmé k ose o.
Poloha bodu A je určena třemi údaji (např. kartézskými souřadnicemi
Místo stanovení polohy tří pevných bodů v tělese, vázaných relacemi
(5,2)
lze
stanovit polohu tělesa v prostoru i jinými šesti údaji. Pro východisko
kinematických úvah je nejvhodnější, když stanovíme polohu jednoho bodu, tímto
bodem procházející osy a určíme natočení tělesa vůči této ose. Postup je
znázorněn na obr.39, kde bod je označen A, osa o
a natočení je charak-terizováno úhlem j
mezi přímkou pevnou v tělese značenou
plně a přímkou pevnou v prostoru značenou čárkovaně. Obě přímky tvořící
úhel j jsou kolmé k ose o.
Poloha bodu A je určena třemi údaji (např. kartézskými souřadnicemi
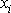 bodu A), směr osy je určen dvěma údaji (např. složkami jednotkového vektoru
bodu A), směr osy je určen dvěma údaji (např. složkami jednotkového vektoru
 ve směru osy o, mezi kterými platí
vztah
ve směru osy o, mezi kterými platí
vztah
 redukující počet nezávislých údajů na dva) a úhel j
representuje jeden údaj. Dohromady máme opět
šest údajů odpovídajících šesti stupňům volnosti tělesa.
redukující počet nezávislých údajů na dva) a úhel j
representuje jeden údaj. Dohromady máme opět
šest údajů odpovídajících šesti stupňům volnosti tělesa.
Přejdeme od stanovení polohy k vyšetřování pohybu tělesa. Nejprve vyšetříme speciální případ, kdy bod A a osa o jím procházející zachovávají po celou dobu pohybu v tělese i v prostoru stálou polohu. Pak jedinou časově proměnou veličinou je úhel j a udáme-li jeho časovou závislost
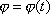 , , |
(5,12) |
bude pohyb plně kinematicky určen. Popsaný pohyb se nazývá otáčení (rotace)
tuhého tělesa kolem pevné osy. Otáčení kolem osy lze popsat jedinou parametrickou
rovnicí
(5,12)
. Je to pohyb s jedním stupněm volnosti. Otáčí-li se těleso
kolem pevné osy, konají všechny jeho body (s výjimkou klidných bodů na ose)
v rovině kolmé k ose o
kruhový pohyb popsaný rovnicemi
(1,42)
. Všechny body mají společnou úhlovou rychlost
 . Zavedeme vektor úhlové rychlosti
. Zavedeme vektor úhlové rychlosti
 (viz též rovnici
(2,24)
) jakožto vektor velikosti
(viz též rovnici
(2,24)
) jakožto vektor velikosti
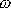 , jehož směr je shodný se směrem osy otáčení. Pak můžeme rychlost
, jehož směr je shodný se směrem osy otáčení. Pak můžeme rychlost
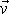 libovolného bodu tělesa otáčejícího se kolem osy vyjádřit jako
libovolného bodu tělesa otáčejícího se kolem osy vyjádřit jako
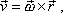 |
(5,13) |
 kde
kde
 je vektor vedený z jednoho pevného bodu
na ose otáčení (např. z bodu A) do místa, v němž se nachází bod,
jehož rychlost
je vektor vedený z jednoho pevného bodu
na ose otáčení (např. z bodu A) do místa, v němž se nachází bod,
jehož rychlost
 chceme určit. Aby výraz
(5,13)
byl správný,
je nutno ještě předpokládat, že smysl vektoru
chceme určit. Aby výraz
(5,13)
byl správný,
je nutno ještě předpokládat, že smysl vektoru
 na ose o
byl zvolen tak, že vektory
na ose o
byl zvolen tak, že vektory
 v uvedeném pořadí tvoří pravotočivý
systém, což lze vyjádřit také tak, že při pohledu ve směru a smyslu
vektoru
v uvedeném pořadí tvoří pravotočivý
systém, což lze vyjádřit také tak, že při pohledu ve směru a smyslu
vektoru
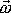 probíhá pohyb ve směru otáčení hodinových ručiček. Vektory
probíhá pohyb ve směru otáčení hodinových ručiček. Vektory
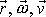 , přímka p pevná v prostoru a proměnný úhel
, přímka p pevná v prostoru a proměnný úhel
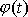 jsou znázorněny na obr.40. Pro velikost v vektoru rychlosti
jsou znázorněny na obr.40. Pro velikost v vektoru rychlosti
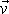 dostáváme z
(5,13)
dostáváme z
(5,13)
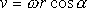 , kde a je úhel mezi vektory
, kde a je úhel mezi vektory
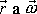 . Výraz
. Výraz
 je však roven kolmé vzdálenosti od osy otáčení bodu, v němž rychlost
je však roven kolmé vzdálenosti od osy otáčení bodu, v němž rychlost
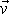 počítáme. Tato vzdálenost je poloměrem
kružnice, po které se zmíněný bod otáčí, a na obr.40 je označena R.
Pro velikost rychlosti kruho-vého pohybu pak dostáváme z
(5,13)
již dříve (viz
(1,37)
) známé vyjádření
počítáme. Tato vzdálenost je poloměrem
kružnice, po které se zmíněný bod otáčí, a na obr.40 je označena R.
Pro velikost rychlosti kruho-vého pohybu pak dostáváme z
(5,13)
již dříve (viz
(1,37)
) známé vyjádření
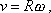 |
(5,13´)
kde
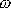 podobně jako v nerovnoměrném kruhovém pohybu je obecnou funkcí času
podobně jako v nerovnoměrném kruhovém pohybu je obecnou funkcí času
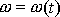 .
.
Dále vyšetříme pohyb tělesa, při kterém jeden jeho bod můžeme si jej představit jako bod A z obr.39 zachovává po celou dobu pohybu v tělese i prostoru stálou polohu. Takový pohyb nazveme otáčení tuhého tělesa kolem pevného bodu.
Je možno dokázat, že v každém okamžiku lze otáčení tuhého tělesa kolem pevného bodu vyjádřit jako otáčení tuhého tělesa kolem pevné osy procházející pevným bodem.
V průběhu času se mění jak poloha osy otáčení v prostoru a v tělese tak i velikost rychlosti otáčení kolem osy. Rychlost libovolného bodu tělesa otáčejícího se kolem pevného bodu lze pak vyjádřit vzorcem (5,13)
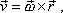 |
kde však nyní nejen velikost vektoru
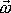 , ale i jeho směr se s časem mění, tedy celý vektor úhlové rychlosti
, ale i jeho směr se s časem mění, tedy celý vektor úhlové rychlosti
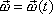 |
(5,14) |
je funkcí času.
Právě vyslovené tvrzení je obsahem Eulerovy věty, jejíž důkaz může čtenář najít např. v [11], [14], [16].

 Pro pohyb, při kterém v každém okamžiku všechny body tělesa mají stejný vektor
rychlosti
Pro pohyb, při kterém v každém okamžiku všechny body tělesa mají stejný vektor
rychlosti
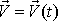 , užíváme ně-kterého z názvů posuvný, postupný pohyb
nebo translace. Jelikož časový průběh rychlosti
všech bodů tělesa je stejný, mají trajektorie všech bodů při posuvném pohybu
shodný tvar a liší se pouze v důsledku různé počáteční polohy bodů.
Trajektorie několika bodů tuhého tělesa konajícího posuvný pohyb jsou
znázorněny na obr.41.
, užíváme ně-kterého z názvů posuvný, postupný pohyb
nebo translace. Jelikož časový průběh rychlosti
všech bodů tělesa je stejný, mají trajektorie všech bodů při posuvném pohybu
shodný tvar a liší se pouze v důsledku různé počáteční polohy bodů.
Trajektorie několika bodů tuhého tělesa konajícího posuvný pohyb jsou
znázorněny na obr.41.
Libovolný pohyb tuhého tělesa lze složit z posuvného pohybu (translace) a otáčení
(rotace) kolem pevného bodu. Toto tvrzení bývá nazýváno Chaslesovou větou
(např. [11]). Rychlost
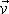 libovolného bodu tuhého tělesa určíme jako součet rychlosti
libovolného bodu tuhého tělesa určíme jako součet rychlosti
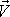 jed-noho libovolně zvoleného bodu tělesa A
a rychlosti
jed-noho libovolně zvoleného bodu tělesa A
a rychlosti
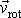 otáčení kolem tohoto zvole-ného bodu. Rychlost
otáčení kolem tohoto zvole-ného bodu. Rychlost
 bodu A pokládá-me za rychlost posuvného
pohybu tělesa a rychlost rotace kolem bodu A určíme dle vzorce
(5,13)
,
stejně jako v případě rotace kolem pevného bodu. Pro rychlost
bodu A pokládá-me za rychlost posuvného
pohybu tělesa a rychlost rotace kolem bodu A určíme dle vzorce
(5,13)
,
stejně jako v případě rotace kolem pevného bodu. Pro rychlost
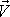 libo-volného bodu tělesa tak dostáváme vyjádření
libo-volného bodu tělesa tak dostáváme vyjádření
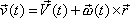 , , |
(5,16) |
kde
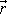 je vektor vedený z bodu A do bodu, jehož rychlost
je vektor vedený z bodu A do bodu, jehož rychlost
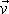 určujeme (viz obr.42). Popis pohybu, jak je
formulován rovnicí
(5,16)
, vychází z určení polohy tuhého tělesa způsobem
naznačeným na obr.39. Určíme rychlost pohybu bodu A a rotaci kolem osy o.
Osu o však v rovnici
(5,16)
nevolíme
libovolně jako při určení polohy tělesa, ale je to okamžitá osa otáčení tělesa.
Osa otáčení je význačná tím, že zachovává svou polohu v prostoru i
v tělese. Okamžitá osa otáčení je v rovnici
(5,16)
uvažována jako osa
procházející pohyblivým bodem A. Nemůžeme tedy mluvit přímo o zachování polohy
v prostoru, ale v diferenciálním časovém intervalu zachovává osa svůj
směr v prostoru.
určujeme (viz obr.42). Popis pohybu, jak je
formulován rovnicí
(5,16)
, vychází z určení polohy tuhého tělesa způsobem
naznačeným na obr.39. Určíme rychlost pohybu bodu A a rotaci kolem osy o.
Osu o však v rovnici
(5,16)
nevolíme
libovolně jako při určení polohy tělesa, ale je to okamžitá osa otáčení tělesa.
Osa otáčení je význačná tím, že zachovává svou polohu v prostoru i
v tělese. Okamžitá osa otáčení je v rovnici
(5,16)
uvažována jako osa
procházející pohyblivým bodem A. Nemůžeme tedy mluvit přímo o zachování polohy
v prostoru, ale v diferenciálním časovém intervalu zachovává osa svůj
směr v prostoru.
 Zjistíme, jak závisí vyjádření rychlosti
libovolného bodu tělesa na volbě bodu A. Zvolíme v tělese dva body: bod A,
který se pohybuje rychlostí
Zjistíme, jak závisí vyjádření rychlosti
libovolného bodu tělesa na volbě bodu A. Zvolíme v tělese dva body: bod A,
který se pohybuje rychlostí
 a bod A´, který se pohybuje rychlostí
a bod A´, který se pohybuje rychlostí
 (obr.43). Určíme rychlost
(obr.43). Určíme rychlost
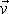 libovolného bodu tělesa, který je na obr.43
označen X. Pokládáme-li bod A za bod, vůči kterému je uvažována rotace tělesa, je
libovolného bodu tělesa, který je na obr.43
označen X. Pokládáme-li bod A za bod, vůči kterému je uvažována rotace tělesa, je
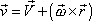 . . |
(5,16) |
Pokládáme-li
bod A´ za střed rotace, dostáváme pro rychlost
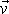 vyjádření
vyjádření
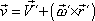 . . |
(5,17) |
V rovnici
(5,17)
je
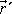 vektor s počátkem v bodě A´ a koncem v bodě X a
vektor s počátkem v bodě A´ a koncem v bodě X a
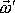 vektor úhlové rychlosti rotace tělesa vůči bodu A´. Vyjádříme rychlost
vektor úhlové rychlosti rotace tělesa vůči bodu A´. Vyjádříme rychlost
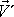 bodu A´ dle vzorce
(5,16)
, dostáváme
bodu A´ dle vzorce
(5,16)
, dostáváme
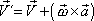 . . |
(5,18) |
Vektor
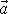 má počátek v bodě A a konec v bodě A´. Mezi vektory
má počátek v bodě A a konec v bodě A´. Mezi vektory
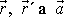 platí vztah
platí vztah
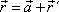 . . |
(5,19) |
Dosadíme-li vyjádření vektoru
 dle
(5,19)
do rovnice
(5,16)
, dostáváme
dle
(5,19)
do rovnice
(5,16)
, dostáváme
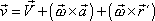 . . |
Dle (5,18)
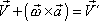 , , |
a tedy
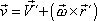 . . |
(5,20) |
Porovnáním rovnic (5,20) a (5,17) dostáváme důležitou rovnost
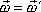 . . |
(5,21) |
Úhlová rychlost otáčení tělesa
 nezávisí na volbě bodu, vůči kterému otáčení
uvažujeme. Rychlosti dvou různých bodů tělesa zde označené
nezávisí na volbě bodu, vůči kterému otáčení
uvažujeme. Rychlosti dvou různých bodů tělesa zde označené
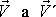 jsou obecně různé. Velikost posuvné
rychlosti uvažované v rovnici
(5,16)
na volbě bodu A závisí.
jsou obecně různé. Velikost posuvné
rychlosti uvažované v rovnici
(5,16)
na volbě bodu A závisí.
Rovnice (5,16)
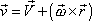 |
(5,16) |
je základní rovnicí kinematiky tuhého tělesa. Určuje významnou kinematickou veličinu rychlost libovolného bodu tuhého tělesa z časového průběhu dvou vektorových funkcí
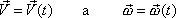 . . |
(5,22) |
V tomto smyslu jsou rovnice
(5,22)
analogické kinematickým rovnicím
(1,3)
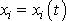 , resp.
(1,4)
, resp.
(1,4)
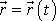 , hmotného bodu. Analogie však není úplná.
Rovnice
(1,3)
, resp.
(1,4)
, určují trajektorii hmotného bodu, tj. časovou
závislost jeho polohy. Rovnice
(5,16)
určuje pouze rychlost libovolného bodu
tuhého tělesa v jednom okamžiku a ne jeho trajektorii.
, hmotného bodu. Analogie však není úplná.
Rovnice
(1,3)
, resp.
(1,4)
, určují trajektorii hmotného bodu, tj. časovou
závislost jeho polohy. Rovnice
(5,16)
určuje pouze rychlost libovolného bodu
tuhého tělesa v jednom okamžiku a ne jeho trajektorii.
Trajektorie jednotlivých bodů tuhého tělesa nelze snadno stanovit, i když známe funkce
(5,22)
. Pomineme-li potíže při integraci rovnice
(5,16)
, podstatnou překážkou
stanovení trajektorií je určení vektoru
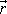 , který vystupuje v rovnici
(5,16)
. V soustavě souřadné pevné
v prostoru nelze jednoduše stanovit určitý bod tuhého tělesa.
Pokládáme-li
, který vystupuje v rovnici
(5,16)
. V soustavě souřadné pevné
v prostoru nelze jednoduše stanovit určitý bod tuhého tělesa.
Pokládáme-li
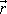 za vektor stálý v prostoru, budou se
v jeho koncovém bodě v průběhu času nacházet různé body tuhého
tělesa. Budeme-li pokládat vektor
za vektor stálý v prostoru, budou se
v jeho koncovém bodě v průběhu času nacházet různé body tuhého
tělesa. Budeme-li pokládat vektor
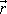 za vektor, jehož koncový bod se nachází ve
zcela určitém bodu tuhého tělesa, stává se rovnice
(5,16)
neurčitou. Časovou
závislost vektoru
za vektor, jehož koncový bod se nachází ve
zcela určitém bodu tuhého tělesa, stává se rovnice
(5,16)
neurčitou. Časovou
závislost vektoru
 pevného v tělese neznáme totiž dříve,
než určíme trajektorie bodů tuhého tělesa. Některé způsoby řešení uvedeného
problému ukážeme v kapitole 6.
pevného v tělese neznáme totiž dříve,
než určíme trajektorie bodů tuhého tělesa. Některé způsoby řešení uvedeného
problému ukážeme v kapitole 6.
V minulém odstavci jsme ukázali nedostatky rovnice (5,16) . Přesto je tato rovnice nejpřehlednějším závěrem kinematiky tuhého tělesa. Naznačuje hlavní úkol dynamiky tuhého tělesa, kterým je stanovení dvou vektorových funkcí (5,22) ze znalosti sil působících na těleso.