Soustavou hmotných bodů rozumíme více hmotných bodů. Jejich
počet označíme N. Soustava je určena,
známe-li hmotnosti
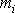 a polohy jednotlivých jejích bodů. Polohu
bodů soustavy můžeme určit např. jejich polohovými vektory
a polohy jednotlivých jejích bodů. Polohu
bodů soustavy můžeme určit např. jejich polohovými vektory
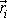 Udáním hodnot
Udáním hodnot
 |
(5,1) |
určíme soustavu. Ke stanovení polohy soustavy je třeba N
polohových vektorů
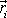 . Každý polohový vektor
. Každý polohový vektor
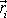 má tři složky souřadnice
má tři složky souřadnice
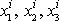 i-tého hmotného bodu.Poloha soustavy je udána 3N souřadnicemi
i-tého hmotného bodu.Poloha soustavy je udána 3N souřadnicemi
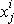 , kde j nabývá hodnot j = 1, 2, 3
a nezávisle i hodnot i = 1, 2, , N.
Pořadové číslo bodu píšeme jako vrchní index u symbolu x , číslo udávající souřadnici jako
spodní index.
, kde j nabývá hodnot j = 1, 2, 3
a nezávisle i hodnot i = 1, 2, , N.
Pořadové číslo bodu píšeme jako vrchní index u symbolu x , číslo udávající souřadnici jako
spodní index.
Počet nezávislých souřadnic (nemusí být kartézské), kterými určíme jednoznačně polohu
nějakého mechanického objektu, nazýváme počtem stupňů volnosti tohoto objektu.
Jsou-li polohové vektory
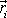 z
(5,1)
vzájemně nezávislé, nazýváme soustavu, která je jimi určena,
volnousoustavou hmotných bodů. Volná soustava hmotných bodů má pak zřejmě 3N
stupňů volnosti. Je-li v
(5,1)
N = 1, máme místo soustavy
jediný bod, tj. objekt, jehož chování jsme vyšetřovali v předcházejících
kapitolách. Počet stupňů volnosti hmotného bodu je tedy tři. Může-li se hmotný
bod pohybovat pouze v ploše, má dva stupně volnosti a hmotný bod vázaný na
křivku jeden stupeň volnosti.
z
(5,1)
vzájemně nezávislé, nazýváme soustavu, která je jimi určena,
volnousoustavou hmotných bodů. Volná soustava hmotných bodů má pak zřejmě 3N
stupňů volnosti. Je-li v
(5,1)
N = 1, máme místo soustavy
jediný bod, tj. objekt, jehož chování jsme vyšetřovali v předcházejících
kapitolách. Počet stupňů volnosti hmotného bodu je tedy tři. Může-li se hmotný
bod pohybovat pouze v ploše, má dva stupně volnosti a hmotný bod vázaný na
křivku jeden stupeň volnosti.
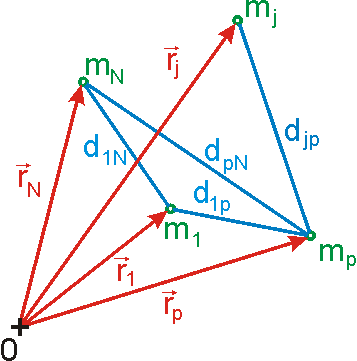 Kromě volné soustavy hmotných bodů zavedeme tuhou soustavu hmotných bodů. Tuhá
soustava má neproměnné vzdálenosti mezi jednotlivými hmotnými body soustavy. Na
obr.37 je znázorněna soustava N
hmotných bodů. Jsou-li vzdálenosti
Kromě volné soustavy hmotných bodů zavedeme tuhou soustavu hmotných bodů. Tuhá
soustava má neproměnné vzdálenosti mezi jednotlivými hmotnými body soustavy. Na
obr.37 je znázorněna soustava N
hmotných bodů. Jsou-li vzdálenosti
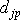 ( j a p nabývají nezávisle hodnot 1, 2, ,N,
z nichž některé jsou na obrázku znázorněny, neproměnné, jedná se o tuhou
soustavu hmotných bodů. Z geometrického názoru je zřejmé, že udáním polohy
tří hmotných bodů tuhé soustavy, které všechny neleží v jedné přímce, je
jednoznačně určena poloha všech bodů soustavy. Udání polohy tří bodů znamená
stanovení hodnot tří polohových vektorů
( j a p nabývají nezávisle hodnot 1, 2, ,N,
z nichž některé jsou na obrázku znázorněny, neproměnné, jedná se o tuhou
soustavu hmotných bodů. Z geometrického názoru je zřejmé, že udáním polohy
tří hmotných bodů tuhé soustavy, které všechny neleží v jedné přímce, je
jednoznačně určena poloha všech bodů soustavy. Udání polohy tří bodů znamená
stanovení hodnot tří polohových vektorů
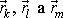 , kde
, kde
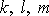 jsou pevně daná, vzájemně různá, celá čísla z intervalu
jsou pevně daná, vzájemně různá, celá čísla z intervalu
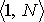 . Tři vektory
. Tři vektory
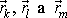 mají devět souřadnic
mají devět souřadnic
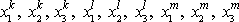 . Vzdálenosti
. Vzdálenosti
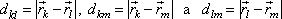 |
(5,2) |
bodů
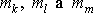 jsou pevně dány, a proto není všech devět souřadnic
jsou pevně dány, a proto není všech devět souřadnic
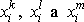 nezávislých. Platí mezi nimi vztahy
nezávislých. Platí mezi nimi vztahy
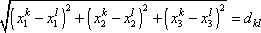 |
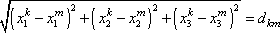 , , |
(5,3) |
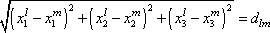 |
které jsou do složek rozepsanými
rovnicemi
(5,2)
. Tři rovnice
(5,3)
se známými hodnotami na pravé straně
ukazují, že z devíti souřadnic
 můžeme nezávisle volit pouze šest, zbývající
tři pak již určíme z rovnice
(5,3)
. Poloha tuhé soustavy hmotných bodů je
určena udáním šesti souřadnic, její počet stupňů volnosti je 6.
můžeme nezávisle volit pouze šest, zbývající
tři pak již určíme z rovnice
(5,3)
. Poloha tuhé soustavy hmotných bodů je
určena udáním šesti souřadnic, její počet stupňů volnosti je 6.
Shrneme nejčastěji uvažované stupně volnosti. Volný hmotný bod má tři stupně volnosti, bod vázaný na plochu má dva stupně volnosti, bod vázaný na křivku jeden stupeň volnosti. Volná soustava N hmotných bodů má 3N stupňů volnosti. Tuhá soustava hmotných bodů a dále probírané tuhé těleso mají šest stupňů volnosti.
 Důležitým objektem našich dalších úvah bude
tuhé těleso. Pojem tuhé těleso vznikne abstrakcí reálného tělesa. Při této
abstrakci se zachovává tvar a rozložení hmotnosti reálného tělesa, předpokládá
se však, že vzájemné vzdálenosti jednotlivých bodů tělesa zůstávají neproměnné
při libovolných silách působících na těleso. Abstraktní pojem tuhé těleso
umožní především vyšetřit podstatné otázky svázané s rotací reálného
tělesa a dále dá základní představy při vyšetřování problémů, v kterých
nelze zanedbat konečné rozměry reálných těles. Obě tyto otázky nebylo možno
vyšetřit, bylo-li hmotné těleso nahrazeno hmotným bodem. Avšak ani tuhé těleso
nedá správný obraz o chování reálného tělesa v případech, kdy podstatnou
roli hrají pružné nebo obecně reologické vlastnosti (viz II, kapitola 2)
reálného tělesa.
Důležitým objektem našich dalších úvah bude
tuhé těleso. Pojem tuhé těleso vznikne abstrakcí reálného tělesa. Při této
abstrakci se zachovává tvar a rozložení hmotnosti reálného tělesa, předpokládá
se však, že vzájemné vzdálenosti jednotlivých bodů tělesa zůstávají neproměnné
při libovolných silách působících na těleso. Abstraktní pojem tuhé těleso
umožní především vyšetřit podstatné otázky svázané s rotací reálného
tělesa a dále dá základní představy při vyšetřování problémů, v kterých
nelze zanedbat konečné rozměry reálných těles. Obě tyto otázky nebylo možno
vyšetřit, bylo-li hmotné těleso nahrazeno hmotným bodem. Avšak ani tuhé těleso
nedá správný obraz o chování reálného tělesa v případech, kdy podstatnou
roli hrají pružné nebo obecně reologické vlastnosti (viz II, kapitola 2)
reálného tělesa.
Tuhé těleso je určeno, udáme-li jeho hustotu r jako funkci sou-řadnic
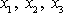 ;
;
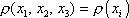 . . |
(5,4) |
Hustotou r zde rozumíme limitní hodnotu poměru hmotnosti m obsažené v objemu V k objemu V, zmenšujeme-li libovolným způso-bem objem V obklopující bod, v němž hustotu chceme stanovit;
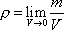 . . |
(5,5) |
Přitom, jak bývá ve fyzice zvykem, bez důkazu předpokládáme existenci limity.
Představa o existenci limity vychází v tomto případě z představy spojitého rozložení hmotnosti v tělese. V těchto mechanických úvahách ignorujeme atomickou strukturu hmoty. Limitní proces musíme zastavit dříve, než lineární rozměry zvolených objemů (krychliček) dosáhnou přibližně rozměrů atomických nehomogenit, tj. řádu 1010 m. Hustota tělesa přiřazená tímto limitním procesem jeho jednomu geometrickému bodu je tak pro daný bod jakousi nejpravděpodobnější hodnotou hustoty z jeho dostatečně širokého okolí. Při tomto postupu odpovídajícímu přibližně postupům matematické teorie distribucí (např. [56]) jsou úvahy vycházející z dřívějšího chápání analýzy, jako nauky o malých přírůstcích, oprávněné.
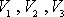 , které lze použít, zjistíme-li jejich hmotnosti
, které lze použít, zjistíme-li jejich hmotnosti
 ke stanovení limity
(5,5)
, tj. hustoty v bodě A.
ke stanovení limity
(5,5)
, tj. hustoty v bodě A.
Limitu
(5,5)
jakožto limitu podílu lze pokládat za derivaci
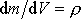 . Tuto derivaci můžeme přepsat jako vztah mezi diferenciály
. Tuto derivaci můžeme přepsat jako vztah mezi diferenciály
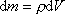 . . |
(5,6) |
Zadáním výrazu
(5,4)
je současně určena i hranice tuhého tělesa. Těleso se nachází tam,
kde hustota je různá od nuly (
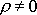 ). Mimo těleso je hustota rovná nule (
). Mimo těleso je hustota rovná nule (
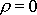 ).
).
Soustava hmotných bodů je určena údaji (5,1) . Z nich výrazem
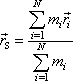 |
(5,7) |
určíme polohu bodu, který nazveme hmotný střed
soustavy hmotných bodů. Poloha
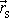 hmotného středu soustavy je plně určena
rozložením hmotných bodů soustavy a zpravidla nesplývá s polohou žádného
bodu soustavy. Pro tuhé těleso definuje polohu
hmotného středu soustavy je plně určena
rozložením hmotných bodů soustavy a zpravidla nesplývá s polohou žádného
bodu soustavy. Pro tuhé těleso definuje polohu
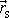 hmotného středu podíl objemových integrálů
hmotného středu podíl objemových integrálů
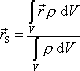 , , |
(5,8) |
kde obor integrace zahrnuje celý objem tělesa. V tuhém tělese hmotný střed
obvykle splývá s některým bodem tělesa. Dle rovnice
(5,6)
zřejmě
 , kde M je označena celková hmotnost tělesa. Taktéž
v rovnici
(5,7)
, kde M je označena celková hmotnost tělesa. Taktéž
v rovnici
(5,7)
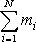 je rovna celkové hmotnosti M
soustavy hmotných bodů. Z rovnic
(5,7)
a
(5,8)
plynou pro
jednotlivé souřadnice hmotného středu, které označíme
je rovna celkové hmotnosti M
soustavy hmotných bodů. Z rovnic
(5,7)
a
(5,8)
plynou pro
jednotlivé souřadnice hmotného středu, které označíme
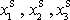 , rovnice:
, rovnice:
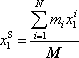 |
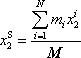 |
neboli složkově
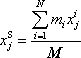 |
(5,7´) |
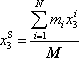 |
a
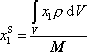 |
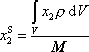 |
neboli složkově
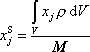 |
(5,8´) |
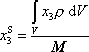 |
Hmotný střed tělesa je bod, který je též známý pod názvem těžiště tělesa. Důvod tohoto druhého označení bude vysvětlen v čl. 5.7.
Součet
(5,7´)
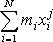 pro soustavu hmotných bodů je pro tuhé těleso nahrazen integrálem
pro soustavu hmotných bodů je pro tuhé těleso nahrazen integrálem
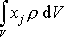 přes objem tělesa V. Např. diskrétní hodnoty souřadnice
přes objem tělesa V. Např. diskrétní hodnoty souřadnice
 z první rovnice
(5,7´)
jsou nahrazeny v první rovnici
(5,8´)
spojitě proměnnou
z první rovnice
(5,7´)
jsou nahrazeny v první rovnici
(5,8´)
spojitě proměnnou
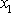 , kterou je nutno v součinu s funkcí všech tří proměnných
, kterou je nutno v součinu s funkcí všech tří proměnných
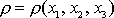 integrovat přes celý objem tělesa V.
Tento postup je typický pro přechod mezi vzorci odvozenými pro soustavu
hmotných bodů a pro tuhé těleso. Výrazy pro soustavu hmotných bodů získáme ve
tvaru
integrovat přes celý objem tělesa V.
Tento postup je typický pro přechod mezi vzorci odvozenými pro soustavu
hmotných bodů a pro tuhé těleso. Výrazy pro soustavu hmotných bodů získáme ve
tvaru
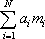 , , |
(5,9) |
kde
 je nějaká veličina vztahující se k i-tému
hmotnému bodu. Analogický výraz pro tuhé těleso má tvar integrálu
je nějaká veličina vztahující se k i-tému
hmotnému bodu. Analogický výraz pro tuhé těleso má tvar integrálu
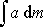 přes hmotnost tělesa. Jelikož je nevhodné integrovat přes hmotnost tělesa, převede se
integrál
přes hmotnost tělesa. Jelikož je nevhodné integrovat přes hmotnost tělesa, převede se
integrál
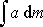 dle vztahu
(5,6)
na integrál
dle vztahu
(5,6)
na integrál
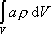 |
(5,10) |
přes objem tělesa V.
Analogie mezi výrazy (5,9) a (5,10) , kterou zde uvádíme bez hlubšího matematického rozboru, je velmi často užívána při odvozování závěrů platných pro tuhé těleso. Většinu dalších výpočtů provedeme pro soustavu hmotných bodů a analogií (5,9) Ž (5,10) výsledky převedeme na tuhé těleso. Přitom na tuhé těleso budeme převádět jen takové závěry, které mají smysl pro tuhou soustavu hmotných bodů. Tuhá soustava hmotných bodů má stejný počet stupňů volnosti jako tuhé těleso a byla zavedena především proto, aby modelovala chování tuhého tělesa. Výpočty pro soustavu hmotných bodů se provádějí ve tvaru součtů a jsou tedy přehlednější než výpočty pro tuhé těleso, které mají integrální tvar.