Málokterá fyzikální vlastnost látek se může měnit v tak širokém rozmezí jako elektrická vodivost. Tak zatímco stříbro má při pokojové teplotě měrnou vodivost γ asi 6.107 (sup>-1, pro diamant platí γ ~ 3.10-17(Ω .m-1). Navíc při nízkých teplotách přecházejí některé látky do tzv. supravodivého stavu s téměř nulovým měrným elektrickým odporem. Při hrubém dělení podle hodnoty elektrické vodivosti se obvykle rozlišují tři typy látek: vodiče, polovodiče a nevodiče. Za vodiče se obvykle považují látky, jejichž měrná vodivost je větší než 106 (sup>- 1. O nevodičích mluvíme v případě, že měrná vodivost je menší než 10-8 (sup>-1. Konečně za polovodiče považujeme látky, pro něž měrná vodivost leží v intervalu (10-8-106) (sup>-1. Uvedené hranice mají ovšem pouze orientační charakter. Vodivost některých látek (zejména polovodičů) se totiž mění i o několik řádů v závislosti na teplotě, osvětlení a jiných faktorech, takže by proto nemělo žádný smysl stanovovat hranice přesně. Fyzikálně hlubším znakem než hodnota měrné vodivosti je její teplotní závislost. Později uvidíme, že velké množství polovodičů má velkou teplotní závislost měrné vodivosti, zatímco pro většinu dobrých vodičů (zejména kovů) je její teplotní závislost mnohem menší.
Pro elektrickou vodivost fyzikálně homogenních pevných látek je chara-kteristická velmi dobrá platnost Ohmova zákona až do velmi vysokých hodnot elektrického pole. Chování fyzikálně nehomogenních soustav naopak ve většině případů nelze popsat jen hodnotou elektrické vodivosti, neboť se v takových soustavách uplatňuje působení vtištěných sil. S nejdůležitějšími jevy tohoto druhu se seznámíme v článku 7.3.3.
Charakter vodivosti velmi silně závisí na tom, jaké objekty tvoří nositele proudu. V látkách různého typu mohou náboje přenášet volné elektrony nebo ionizované atomy či molekuly. V prvním případě mluvíme o vodivosti elektronové, ve druhém případě o vodivosti iontové.[57] Pro nepatrnou hmotnost ele-ktronů není elektronová vodivost spojena se znatelným transportem hmoty. Iontovou vodivost transport hmoty naopak vždy doprovází.
Iontová vodivost v pevných látkách se vyskytuje zejména v iontových krystalech (např. NaCl, AgCl, AgBr a dalších), jejichž krystalová mřížka je vybudována z kladných a záporných iontů. Některé z nich se mohou účinkem vnějšího elektrického pole přemisťovat, čímž přispívají ke zvodivění krystalu. Dále se ion tová vodivost vyskytuje u některých nekrystalických pevných látek, například u skel.
Iontová vodivost zpravidla se vzrůstající teplotou silně vzrůstá. Tento vzrůst vodivosti je podmíněn tím, že při vzrůstající teplotě se zvyšuje počet iontů schopných volného pohybu uvnitř látky.
Jak bylo již uvedeno, je iontová vodivost vždy spojena s transportem látky, který je vždy konečným kritériem, zda u dané látky jde o vodivost iontovou či elektronovou. V látce, kterou delší dobu procházel iontový proud, jsou vždy pozorovatelné změny. Necháme-li například procházet proud krystalem chloridu sodného NaCl, můžeme po určité době pozorovat vylučování sodíku na ploše tvořící záporný pól. Zkušenost totiž ukazuje, že při nepříliš vysoké teplotě jsou v krystalové mřížce pohyblivé pouze ionty Na+. Vylučování chloru na kladné elektrodě je patrné teprve při teplotách blízkých bodu tání, kdy se zvyšuje i pohyblivost iontů Cl-. Množství vyloučené látky je úměrné prošlému náboji a splňuje Faradayovy zákony elektrolýzy (viz článek 7.4.2).
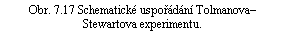
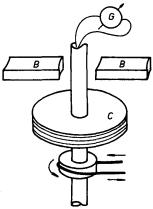
Kovy a polovodiče jsou typickými představiteli látek s elektronovou vodivostí. Současná fyzika pevných látek má k dispozici velké množství experimentálních i teoretických argumentů pro podporu tohoto tvrzení. Z historického hlediska je pro svou principiální jednoduchost a názornost významný Tolmanův-Stewartův experiment, jehož výsledky byly publikovány v roce 1917. Jde o elektromechanický pokus, který vychází z předpokladu, že při prudkém zabrždění pohybujícího se kovu musí dojít k vzájemnému pohybu mezi systémem volných elektronů a krystalovou mřížkou, což se projeví proudovým impulsem. Jednoduchým výpočtem (viz dálší výklad) lze ukázat, že celkový proteklý náboj je úměrný poměru náboje q a hmotnosti m nositelů proudu, tj. veličině q/m. Zmínění autoři provedli experiment pro případ stříbra, mědi a hliníku. Pro q/m získali hodnoty ležící v intervalu (1,49 až 1,60). 1011 C.kg-1, současná nejpřesnější hodnota pro elektron činí 1,758820174(71).1011 C. kg-1 (viz Dodatek 2.).
Tolman a Stewart realizovali experiment způsobem, jehož schéma je uvedeno na obr. 7.17. Ze zkoumaného kovu zhotovili cívku C o značném počtu závitů, kterou připojili do obvodu balistického galvanometru G schopného měřit celkový prošlý náboj Q. Cívku uvedli do rychlé rotace a po určité době ji pomocí brzdicích čelistí B během krátkého časového intervalu Δ t zabrzdili a sledovali prošlý náboj.
Po zabrzdění cívky budou volní nositelé náboje určitou dobu v pohybu vůči krystalové mřížce kovu a budou tedy reprezentovat jistý elektrický proud I. Postupně budou předávat svoji kinetickou energii krystalové mřížce ve formě tepla, které může být rovněž vyjádřeno jako Jouleovo teplo. Uvažujeme vodič délky l a průřezu S, který v jednotce objemu obsahuje n0 volných nositelů nesoucích náboj q a majících hmotnost m. Nechť celkový elektrický odpor vodiče je R, jeho počáteční rychlost v 0, která se zbrzdí na nulu během časového intervalu Δ t . Jestliže za velmi krátký časový interval dt poklesne rychlost v nositele o - d v a obvodem proteče elektrický náboj dQ = I dt , lze pro tento časový interval vyjádřit energetickou bilanci ve tvaru
 |
odkud po integraci v mezích (v 0, 0) můžeme vyjádřit celkový prošlý náboj
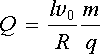 . . |
(7.18) |
Autoři ve svém experimentu používali cívku o celkové délce vodiče asi 500 m. Používaná obvodová rychlost cívky byla 300 m.s-1 a doba brzdění Δ t ~ 0,1s.


Průchod elektrického proudu kovem či polovodičem je doprovázen obecným jevem spočívajícím ve vzniku příčné intenzity elektrického pole, je-li vzorek vložen do příčného pole magnetického. Tento jev, nazývaný Hallovým jevem, má rovněž značnou důležitost pro objasnění mechanismu elektrické vodivosti daného vodiče. Geometrická konfigurace umožňující pozorování Hallova jevu je zobrazena na obr. 7.18. Vnější elektrické pole E x orientované ve směru osy x budí ve vzorku elektrický proud o hustotě j x. Přiložíme-li magnetické pole B z ve směru osy z, objeví se ve vzorku příčné elektrické pole E H,y ve směru osy y, které na vzorku vytvoří měřitelné příčné napětí UH = EH,y d. Intenzita EH,y, respektive napětí UH se nazývá Hallovou intenzitou, respektive Hallovým napětím. Experiment ukazuje, že Hallova intenzita je úměrná proudové hustotě jx a magnetické indukci Bz
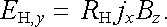 |
(7.19a) |
Konstanta RH, která nezávisí na rozměrech vzorku, se nazývá Hallovou konstantou, a představuje důležitou charakteristiku daného vodiče.
Hallův odpor
Vedle Hallovy konstanty
R
H
se k charakterizaci Hallova jevu užívá i tzv.
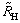 definovaný jako
poměr Hallova napětí UH
a proudu Ix = jxad,
definovaný jako
poměr Hallova napětí UH
a proudu Ix = jxad,
reprezentovaného hustotou jx ve vzorku o průřezu S = ad (viz obr. 7.18). Vzhledem k tomu, že vzorek má velmi často tvar tenkého proužku, lze v těchto případech proud tekoucí ve směru osy x chápat jako proud plošný IS,x = jS,xd, přičemž jS,x = jxad. Pro Hallův odpor tedy platí

a Hallovo napětí respektive Hallovu intenzitu je pak možné alternativně k (7.19a) vyjádřit vztahy
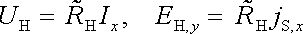 , , |
(7.19b) |
obsažena v Hallově odporu
které reprezentují explicitní závislost UH na proudu Ix, (respektive EH na proudové hustotě jS,x ), zatímco závislost na magnetickém poli je implicitně
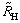 .
.
Zajímavé je, že Hallovo napětí, a tedy i Hallova konstanta RH, může mít pro různé materiály nejen různé hodnoty, ale i různá znamení. Například zatímco pro stříbro je RH(Ag) = - 8,4 . 10-11 m3(As)-1, pro zinek platí RH(Zn) = + 3,3 . 10- 11 m3(As)-1. V článku 7.6.4, ve kterém vyložíme jednoduchou teorii Hallova jevu, ukážeme, že kladné znamení Hallovy konstanty souvisí s podílem tzv. děrové vodivosti na celkové vodivosti látky. Vedle již zmíněné možnosti studia mechanismu elektrické vodivosti látek má Hallův jev významné aplikace i v experimentální technice, především pro měření magnetického pole. Průmy-slově vyráběné magnetometry s Hallovou sondou dnes prakticky vytlačily klasické přístroje založené na jevu elektromagnetické indukce (viz kapitola 4).[58]
V článku 7.1.2 bylo poukázáno na souvislost elektronové struktury látky s její elektrickou vodivostí. Bylo ukázáno (srov. obr. 7.5), že látky, které za teploty absolutní nuly obsahují jen zcela zaplněné a zcela prázdné energetické pásy, jsou při dostatečně nízkých teplotách nevodiče, zatímco látky s pásy zaplněnými částečně jsou vodiče. Při vyšších teplotách je skutečné chování látek právě klasifikovaných jako nevodiče dáno šířkou pásu zakázaných energií Eg mezi posledním zaplněným (valenčním) a prvním prázdným (vodivostním) pásem. Při nenulové teplotě mohou být totiž některé elektrony tepelně excitovány, takže překonají energii zakázaného pásu a obsadí některé stavy v prázdném vodivostním pásu, čímž se současně uvolní odpovídající stavy pásu valenčního. Látka v takovém stavu je pak schopna vést elektrický proud. Pravděpodobnost tepelné excitace při dané teplotě ovšem klesá se vzrůstající šířkou zakázaného pásu. Látky s vysokou hodnotou Eg budou i za vyšších teplot nevodiče, látky s nízkou hodnotou Eg se budou chovat jako polovodiče. Například velmi dobrý nevodič diamant, který má při pokojové teplotě měrnou vodivost γ = 3.10-17(Ω .m)-1, má šířku zakázaného pásu Eg = 5,4 eV. Naproti tomu krystal velmi čistého germania má při pokojové teplotě již měrnou vodivost γ ~ 20(Ω .m)-1, přičemž šířka zakázaného pásu germania Eg ~ 0.66 eV. Obě látky přitom mají krystalovou strukturu stejného typu.
Vlastnosti polovodičů podrobněji studujeme v článku 7.3.4. Uvidíme, že při dané teplotě je vodivost polovodiče velmi silně závislá na čistotě. Z tohoto důvodu je třeba uvedenou hodnotu měrné vodivosti germania považovat jen za řádově informativní.
Většina prvků kovového charakteru a jejich slitin patří mezi dobré vodiče. Je pro ně charakteristická velmi dobrá platnost Ohmova zákona. Důležitou charakteristiku elektrické vodivosti kovů tvoří její teplotní závislost, která je zpravidla nevýrazná ve srovnání s jinými typy pevných látek, například s polovodiči. Obecně řečeno, se vzrůstající teplotou elektrická vodivost kovů klesá, tj. měrný odpor roste. V okolí pokojových teplot je zpravidla možné s dobrou přesností vyjádřit měrný odpor kovu jako lineární funkci teploty. V širším oboru teplot a při větších nárocích na přesnost, je možné teplotní závislost měrného odporu aproximovat polynomem druhého stupně. Označíme-li ρ R(t) měrný odpor při teplotě t v Celsiově stupnici, ρ R,0 měrný odpor při 0 °C, platí
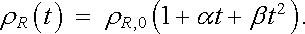 |
(7.20) |
Tabulka 7.7 Parametry elektrické vodivosti vybraných kovů a slitin.
|
látka |
rezistivita γ (Ω .m-1) |
tepl. součinitel odporu α (K-1) |
|
stříbro měď platina železo (čistoty 99,98%) olovo hliník mosaz (Cu 66%,Zn 34%) nichrom konstantan (Cu 84%, Ni 43%) manganin (Cu 84%, Mn 12%, Ni 4%) |
6,14 . 107 5,8 1,0 1,0 0,45 3,54 1,4 0,1 0,2 0,23 |
4,0 . 10-3 4 4 5 4 4 2 4 0,01 0,002 |
Veličiny α a β jsou lineární a kvadratický teplotní součinitel odporu, které je třeba pro jednotlivé kovy určit měřením.
Pro získání konkrétní představy uvádíme v tabulce 7.7 hodnoty měrné vodivosti (rezistivity) při pokojové teplotě a teplotní součinitel odporu α některých kovů. Z tabulky jsou vidět některé závislosti, které mají obecnější charakter. Obecně řečeno, čisté kovy mají větší teplotní součinitel odporu než jejich slitiny. U některých slitin připravovaných za tímto účelem (konstantan, manganin) je možné dokonce dosáhnout snížení o několik řádů. Uváděné prvky mají přitom téměř stejný součinitel odporu, i když se hodnoty jejich měrné vodivosti značně liší. Uváděné slitiny mají dále řádově menší měrnou vodivost než příslušné čisté kovy.
Závislosti demonstrované na několika příkladech podle tabulky 7.7 mají obecnější platnost a souvisí s mechanismem pohybu nositelů proudu. Ukazuje se, že pro hodnotu měrné vodivosti (respektive měrného odporu) je určující interakce vodivostních elektronů s krystalovou mřížkou kovu. Tyto elektrony interagují s krystalovou mřížkou především prostřednictvím jejího elektrického pole, přičemž na hodnotu měrného odporu mají vliv zejména odchylky od jeho periodičnosti. Obvykle se mluví o rozptylu elektronů na nehomogenitách, které v zásadě mohou být způsobeny příčinami dvojího druhu: příměsemi cizích atomů a tepelnými kmity atomů krystalové mřížky. Experiment ukazuje, že při malých koncentracích rozptyl vodivostních elektronů způsobený příměsemi téměř nezávisí na teplotě. Naproti tomu rozptyl vlivem tepelných kmitů na teplotě samozřejmě závisí. Uvedenou skutečnost vyjadřuje tzv. Matthiessenovo pravidlo. Celkový měrný odpor kovu ρ R s malou koncentrací příměsí je dán součtem teplotně nezávislého příspěvku ρ R,p vyjadřujícího rozptyl vodivostních elektronů na cizích atomech a teplotně závislého příspěvku ρ R,k(T) charakterizujícího rozptyl na tepelných kmitech mřížky
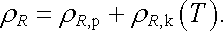 |
(7.21) |
Matthiessenovo pravidlo dovoluje kvalitativně pochopit závislosti demonstrované v tabulce 7.7. V čistých kovech je měrný odpor v zásadě dán jen příspěvkem ρ R,k(T) a má charakteristickou teplotní závislost, která bude diskutována v dalším výkladu. U kovů s příměsemi a u slitin naopak hraje hlavni roli rozptyl na nehomogenitách ve složení krystalu, s nulovou či menší teplotní závislostí.
Jak bylo ukázáno, měrná vodivost kovu je velmi závislá na jeho čistotě. Proto se u velmi čistých kovů používá měrné vodivosti (zejména měřené při nízkých teplotách) k charakterizování jejich čistoty. Měrná vodivost je však závislá i na koncentraci poruch krystalové mřížky (vakancí, intersticiál apod.), a je tudíž závislá i na tepelném zpracování a mechanické deformaci. Studium vodivosti je důležitou metodou pro studium poruch krystalové mřížky. Naproti tomu u některých ušlechtilých kovů v definovaném stavu je měrná vodivost velmi stálou veličinou. Proto se její teplotní závislosti užívá k měření teploty. Nejvýhodnější vlastnosti pro tento účel má platina, pro jejíž teplotní závislost měrného odporu platí vztah typu (7.20)
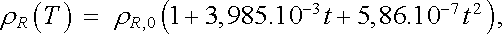 |
(7.22) |
který - jak je známo - tvoří součást Mezinárodní teplotní stupnice (viz například [5, 11]).
Důležitý parametr popisující vlastnosti kmitů krystalové mřížky je tzv. Debyeova teplotaD. Lze proto očekávat, že hodnota měrné vodivosti kovu při dané teplotě bude na Debyeově teplotě závislá. Na Debyeově teplotě jsou závislé i jiné fyzikální vlastnosti kovu, které jsou podmíněny kmity krystalové mřížky. (Jedním z takových parametrů je například měrné teplo - viz např. [10].) Na základě experimentálního studia těchto vlastností pak může být Debyeova teplota určena.
Debyeova teplota je parametr charakterizující tzv. Debyeův model kmitů krystalové mřížky. Tento model vychází z předpokladu, že každý atom, jako bodová částice vázaná kvazielastickými silami v uzlovém bodu krystalu, má tři stupně volnosti a jeho kmity mohou být popsány kmity trojice lineárních harmonických oscilátorů. Celý krystal obsahující N atomů pak může být reprezentován soustavou 3N vzájemně vázaných harmonických oscilátorů. Z mechaniky víme (viz např. [12]), že pro takovou soustavu mohou být zavedeny tzv. vlastní kmity, charakterizované vlastními frekvencemi ω i kterých je celkem 3N. Nejvyšší z těchto vlastních frekvencí ω i,max charakterizuje kmity o nejvyšší možné energii. Debyeova teplota je parametr, který v jednotkách teploty charakterizuje tuto nejvyšší frekvenci ve spektru kmitů krystalové mřížky. Ta je definována vztahem
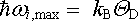 . . |
(7.23) |
Na základě uvedených skutečností nepřekvapí, že měrný odpor čistého kovu při dané teplotě T je do značné míry určen poměrem x = T/D. Tuto souvislost popisuje tzv. Grüneisenova formule, která může být zapsána ve tvaru
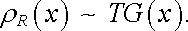 |
(7.24) |
Funkce G(x) je tzv. Grüneisenova funkce. Její tvar je dán určitým integrálem, který nelze jednoduše obecně vyjádřit pomocí elementárních funkcí. Grünei-senův vztah však lze jednoduše aproximovat v mezních situacích T << D a T >> D, pro které z něj plyne [59]
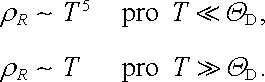 |
(7.25) |
Grüneisenův vztah je velmi dobře splněn pro mnohé kovy ve velmi širokém intervalu teplot. Situaci dobře demonstruje obr. 7.19, který pro řadu čistých kovů vyjadřuje experimentální závislosti ρ R(T)/ ρ R( D) na x = T/D spolu s teoretickou křivkou (reprezentovanou plnou čarou) podle (7.24) .[60] Z uvedeného výkladu je mimo jiné patrná i oprávněnost vztahu (7.20) pro aproximaci teplotní závislosti odporu v okolí pokojové teploty.

Obr. 7.19 Srovnání experimentálních hodnot teplotní závislosti
měrného odporu kovů s Grüneisenovým vztahem.
Vedle teplotní závislosti elektrické vodivosti je pro kovy charakteristická i souvislost mezi elektrickou vodivostí a elektronovým příspěvkem Λ k tepelné vodivosti. Souvislost obou veličin udává experimentálně stanovený Wiedemannův-Franzův zákon, dobře splněný v oboru vyšších teplot. Podle Wiedemannova-Franzova zákona platí vztah
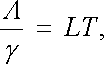 |
(7.26) |
v němž T je absolutní teplota a konstanta L = 2.10-8 W.Ω .K-2 je stejná pro všechny kovy.
Elektrická vodivost je velmi důležitý parametr charakterizující vlastnosti kovů. Mimo jiné sehrála i významnou roli při vymezení platnosti modelu elektronového plynu (srov. čl. 7.1.3). Elementy mikroskopické teorie vodivosti kovů založené na tomto modelu budou uvedeny v článku 7.6.5.
Již v úvodu článku 7.3.1 bylo uvedeno, že vedení elektrického proudu ve fyzikálně nehomogenních soustavách nelze popsat jen elektrickou vodivostí γ . V řadě situací je třeba počítat s působením pole vtištěných elektromotorických sil (srov. čl. 3.2.3), respektive elektromotorických napětí.
Jedním z důležitých jevů tohoto druhu je existence kontaktních napětí mezi kovy při jejich vzájemném styku. Tento jev byl objeven A. Voltou již na konci 18. století. Volta zjistil, že při dotyku dvou různých kovů vzniká mezi nimi samovolně potenciálový rozdíl, jehož velikost je závislá na druhu kovu. Na základě podrobných pokusů sestavil Volta řadu kovů, z nichž se každý při dotyku s libovolným následujícím kovem nabíjí kladně. Tato řada obsahuje kovy:
Al, Zn, Sn, Cd, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd.
Volta dále zjistil, že velikost kontaktního rozdílu potenciálu řady složené z většího počtu kovů (viz obr. 7.20) není závislá na počtu a druhu vnitřních členů řady; závisí pouze na chemickém složení prvního a posledního kovu A, N v řadě.
|
|
|
|
Obr. 7.20 K výkladu vlastností kontaktních napětí. |
Obr. 7.21 Metoda detekce kontaktních napětí elektroskopem. |
Tato specifická vlastnost kontaktního rozdílu potenciálu (kontaktního napětí) komplikuje do jisté míry jejich experimentální studium, neboť kontaktní napětí samotné nemůže za normálních podmínek vytvořit v uzavřeném obvodu elektrický proud. Spojíme-li totiž první kov A a poslední kov N z řady znázorněné na obr. 7.20 jakýmkoliv kovovým vodičem V, nepoteče obvodem proud, poněvadž kontaktní napětí UAV, UVN vyrovnají díky právě uvedené vlastnosti původní kontaktní napětí UAN mezi konci řady. K měření je proto nutné volit jiné, speciální metody.
Na obrázku 7.21 je uvedeno nejprostší uspořádání, které principiálně umožňuje kontaktní napětí detekovat. Na měřicí elektrodu elektroskopu, jehož obal udržujeme pomocí uzemnění Z na nulovém potenciálu, je připojena rovinná deska zhotovená z kovu A. Přes izolační vrstvu I je na ni přiložena deska zhotovená z kovu B a obě desky jsou vodivě spojeny vodičem C. Podle toho co bylo řečeno, vznikne mezi deskami A, B kontaktní napětí nezávislé na materiálu spojky C. Přerušíme-li nyní spojení vodičem C, zůstanou obě desky nabity určitým nábojem Q, jehož velikost odpovídá hodnotě kontaktního napětí a vzájemné kapacitě obou desek. Po oddálení desky B náboj na desce A zůstane a způsobí výchylku elektroskopu.
E
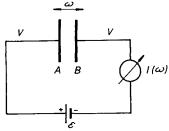
Právě vyložená metoda, i když měření kontaktního napětí principiálně umožňuje, není příliš vhodná pro praktické použití, především pro malou citlivost elektroskopu a pro značnou závislost elektrostatických měření na okolních vlivech. Obrázek 7.22 znázorňuje princip dokonalejší metody. Rovinné desky A, B zhotovené z kovů, jejichž kontaktní napětí chceme měřit, tvoří deskový kondenzátor. Spojíme-li je libovolným vodičem V, nabije se kondenzátor na kontaktní napětí UAB a náboje na jednotlivých deskách budou záviset na velikosti jejich vzájemné kapacity. Při změně vzdálenosti desek se tyto náboje budou měnit a vodičem V poteče proud. Pro praktické měření je výhodné nechat desky kmitat určitou frekvencí ω a přístrojem v obvodu detekovat střídavý proud. Hodnotu kontaktního napětí lze nejsnáze přímo změřit kompenzační metodou. Zařadíme-li totiž do obvodu zdroj vhodné polarity, bude jeho elektromotorické napětí kompenzovat kontaktní napětí. Při rovnosti obou napětí přestane obvodem protékat proud a z odpovídající velikosti kompenzačního elektromotorického napětí zdroje E je možné usuzovat na kontaktní napětí.
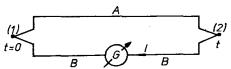
Experimentální zkušenost ukazuje, že kontaktní napětí závisí na teplotě. Tato teplotní závislost je příčinou vzniku tzv. termoelektrických jevů. Uvažujme obvod vytvořený podle obr. 7.23a, zhotovený ze dvou kovů A a B spojených v místech (1) a (2). Bude-li celý obvod na konstantní teplotě, nepoteče vzhledem k uvedeným vlastnostem kontaktního napětí obvodem proud. Budeme-li však spoje (1) a (2) udržovat na různých teplotách T1 a T2, zjistíme, že obvodem proud protéká. Tento jev se nazývá termoelektrickým Seebeckovým jevem. Velikost protékajícího proudu je závislá na druhu obou kovů a na velikosti teplotního rozdílu obou spojů.
Vznik Seebeckova jevu lze kvalitativně snadno vysvětlit na základě teplotní závislosti kontaktního napětí. Budeme-li předpokládat, že kontaktní napětí je funkcí teploty UAB = UAB(T) a označíme-li symbolem R celkový odpor obvodu, bude proud I tekoucí obvodem dán vztahem
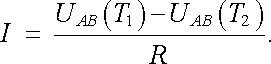 |
(7.27) |
Celkové elektromotorické napětí E S působící v obvodu se nazývá Seebeckovým termoelektrickým napětím a je rovno rozdílu kontaktních napětí obou spojů
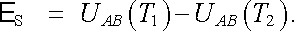 |
(7.28) |
E
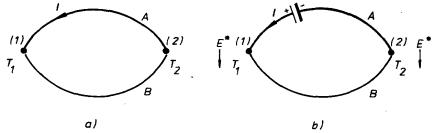
Obr. 7.23 K výkladu termoelektrických jevů: a) Seebeckův jev, b) Peltierův jev.
Inverzním jevem k Seebeckovu jevu je tzv. jev Peltierův. Je možné jej pozorovat v obvodu znázorněném na obr. 7.23b, který je opět zhotoven ze dvou různých kovů A a B a do něhož je zařazen vnější zdroj elektromotorického napětí E . Vnější zdroj vybudí v obvodu proud I a při jeho průchodu se bude teplota jednoho spoje zvyšovat a druhého snižovat. Bude-li proud procházet směrem naznačeným na obrázku, bude teplota spoje (2) vyšší než teplota spoje (1); T1 > T2.
Vedle Seebeckova a Peltierova jevu existuje ještě termoelektrický jev Thomsonův. Tento jev, objevený v polovině devatenáctého století, říká, že elektromotorické napětí vzniká samovolně i v homogenním vodiči, jsou-li jeho jednotlivé části udržovány na různých teplotách. Thomsonův jev může být popsán pomocí Thomsonova elektromotorického napětí E T , které působí mezi částmi vodiče s různými teplotami T 1 , T2. Je zvykem vyjadřovat je ve tvaru
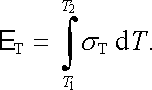 |
(7.29) |
Veličina σ T se nazývá Thomsonův koeficient a závisí na typu látky.
Seebeckův jev se často užívá k měření teploty. Zařízení konstruovaná k tomuto účelu se nazývají termoelektrické články. Sestávají ze tří částí vodičů zhotovených ze dvou vhodných kovů A a B, spojených v místech (1) a (2) (viz obr. 7.24). Jeden se spojů je udržován na definované teplotě (obvykle na teplotě 0 °C, a to ponořením do směsi ledové tříště s vodou), zatímco druhý je umístěn na měřené teplotě t. Termoelektrické napětí, popř. proud I tekoucí obvodem, se měří přístrojem G. Závislost termoelektrického napětí E na teplotě (v Celsiové stupnici) je možné s dostatečnou přesností aproximovat kvadratickou závislostí
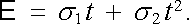 |
(7.30) |

Parametry σ 1 , respektive σ 2 je třeba pro každý termočlánek určit měřením. Pro ilustraci velikosti jevu jsou v tabulce 7.8 uvedeny informativní hodnoty konstanty σ 1 pro nejčastější užívané termočlánky. Podrobnější údaje je možné nalézt například v [11].
Tabulka 7.8 Parametry termoelektrického napětí některých termočlánků
|
termočlánek |
σ 1 (V K-1) |
|
měď-konstantan |
4,0.10-5 |
|
železo-konstantan |
5,0.10-5 |
|
platina-platina rhodium (90%Pt, 10%Rh) |
0,5.10-5 |

Obr. 7.25 K výkladu vzniku kontaktního napětí.
Vznik kontaktního napětí a termoelektrických jevů je podmíněn tím, že některé volné elektrony mohou při styku dvou kovů přecházet z jednoho do druhého. Podrobná kvantitativní analýza těchto jevů vyžaduje podrobnější znalosti o elektronových stavech v kovech a je úkolem fyziky pevných látek. Omezíme se proto jen na názorný kvalitativní výklad mechanismu vzniku kontaktního napětí založený na modelu volných vodivostních elektronů (srov. čl. 7.1.2). Obrázek 7.25a zobrazuje schematicky situaci volných elektronů ve vodivostním pásu dvou kovů A a B při teplotě absolutní nuly za situace, kdy kovy nejsou ve styku. Vodivostní pásy obou kovů jsou zaplněny po Fermiho hladinu, která je v každém kovu jiná. Kov mohou nejsnáze opustit právě tyto elektrony, získají-li energie eφ A a eφ B, nazývané výstupními pracemi. Po styku obou kovů je výchozí situace v obsazení elektronových stavů energeticky nevýhodná. Některé vodivostní elektrony tedy počnou přecházet z kovu A do kovu B, kde mohou obsadit volné stavy s nižší energií. Kov B se počne nabíjet záporně. Proces bude pokračovat tak dlouho, dokud vzniklé elektrické pole nezabrání dalšímu transportu náboje. Rovnovážný stav je tedy charakterizován napětím UAB mezi oběma kovy, které snižuje potenciální energii elektronů v kovu A. Platí UAB = φ B - φ A. Fermiho hladiny v obou kovech jsou vyrovnány. Fenomenologicky může být tento proces popsán polem vtištěných sil intenzity E * mezi oběma kovy.
Užitím pojmu intenzity vtištěných sil E * je možné kvalitativně vyložit i vznik Peltierova jevu. Ve spoji (1) (viz obr. 7.23b) souhlasí směr intenzity E * se směrem proudu. Vtištěné síly tedy urychlují nositele proudu, čímž jim dodávají energii. Tuto energii musí dodávat vodič, čímž se snižuje jeho teplota. Ve spoji (2) je naopak vtištěná intenzita E * orientovaná proti směru proudu. Vnější elektrické pole tedy musí překonávat její působení, čímž dodává vodiči energii zvyšující jeho teplotu.
V článku 7.3.1 byl vyložen rozdíl v elektronové struktuře nevodičů a polovodičů. Při teplotě absolutní nuly jsou obě tyto látky nevodivé, neboť všechny elektrony jsou vázány k jednotlivým atomům a látky neobsahují žádné volné nositele proudu. Rozdíl v obou typech látek je dán jen různou energií vazby elektronů v atomech (jinými slovy různou šířkou zakázaného pásu Eg, která je u polovodičů značně nižší). Mechanismy vzniku elektrické vodivosti polovodičů při nenulových teplotách popíšeme na příkladu dnes nejužívanějšího klasického polovodiče - křemíku.
Křemík má kubickou krystalovou strukturu typu diamantu. Jeho každý atom má čtyři valenční elektrony, které se všechny podílejí na vzájemných vazbách v krystalu. Proto v absolutně čistém křemíku při velmi nízké teplotě nejsou volní nositelé proudu a krystal se chová jako nevodič. Vazby valenčních elektronů však mají malou energii, při vyšších teplotách se snadno poruší, čímž vznikne určitý počet volných elektronů (ve vodivostním pásu - srov. čl. 7.1.2) schopných reagovat na vnější elektrické pole, a tudíž vést proud. Vzniklá uprázdněná místa u jednotlivých atomů, tzv. "díry", které reprezentují "kladné náboje" v krystalové mřížce (a současně neobsazené stavy ve valečním pásu - viz opět čl. 7.1.2), mohou migrovat ve směru elektrického pole a přispívat rovněž k elektrické vodivosti. Celková vodivost ideálně čistého krystalu je tedy dána jednak pohybem uvolněných elektronů a současně pohybem uprázdněných vazeb (děr) u jednotlivých atomů. Takto vzniklý typ vodivosti se nazývá vlastní vodivostí polovodiče.
Je zřejmé, že - díky vlastnostem Fermiho-Diracova rozdělení - počet uvolněných elektronů (a tedy i počet nositelů proudu) poroste silně s teplotou. Podrobnější rozbor mechanismu vodivosti i experiment ukazují, že teplotní závislost měrné vodivosti polovodiče může být v oboru vyšších teplot vyjádřena vztahem
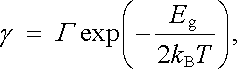 |
(7.31) |
ve kterém Eg je šířka zakázaného pásu (srov. čl. 7.1.2) charakterizující energii vazby valenčních elektronů, Γ je konstanta slabě závislá na teplotě a kB je Boltzmannova konstanta.
V zásadě důležitější než vlastní vodivost je tzv. vodivost příměsová, která je způsobena přítomností cizích atomů. Mohou nastat dva případy: Za prvé mohou mít atomy příměsových prvků větší počet valenčních elektronů než atomy křemíku, za druhé může být jejich počet menší. Probereme speciálně situaci vzniklou přimísením prvků s pěti valenčními elektrony (P, As, Sb) a se třemi valenčními elektrony (B, AI, Ga, In).
Jsou-li v krystalové mřížce germania přítomné atomy s pěti valenčními elektrony, jsou na krystalovou mřížku vázány pouze čtyři elektrony, zatímco pátý je na svůj atom vázán jen velmi nepatrně. Může se tudíž uvolňovat i při relativně nízkých teplotách a zvyšovat vodivost krystalu. Nečistoty dodávající krystalu takto slabě vázané elektrony se nazývají donory a příspěvek k vodivosti působený těmito uvolněnými elektrony nazýváme vodivost typu n.
Jsou-li naopak v krystalové mřížce přítomny atomy se třemi valenčními elektrony, zůstane v místě nečistoty nezaplněna vazba jednoho elektronu k elektronům sousedních atomů křemíku. Do tohoto "volného místa" může přeskočit elektron z neporušené části krystalové mřížky a může v něm být po určitou dobu držen. (Z atomu příměsi tím vznikne záporný iont.) V neporušené části krystalu ovšem vznikne u příslušného atomu vzhledem k chybějícímu elektronu přebytek kladného náboje, tj. podobně jako v případě vlastní vodivosti vznikne díra, která reprezentuje kladný náboj a při působení vnějšího elektrického pole (díky své pohyblivosti v objemu krystalu) může přispívat ke zvýšení vodivosti. Příměsi zachycující elektrony vlastních atomů krystalu se nazývají akceptory a příspěvek k vodivosti vzniklý pohybem děr nazýváme vodivost typu p.
Polovodič, jehož vodivost je způsobena především pohybem děr, se nazývá polovodič typu p. Naopak polovodič, jehož vodivost realizují především volné elektrony, se nazývá polovodič typu n.
Právě uvedené mechanismy vlastní a příměsové vodivosti polovodiče, které jsme vyložili jako důsledek ionizace jednotlivých atomů krystalu, je možné velmi názorně popsat pomocí pásového modelu. Situaci jednotlivých typů vodivosti schematicky znázorňuje obr. 7.26. Obrázek 7.26a se týká vlastní vodivosti. Uvolnění valenčního elektronu atomu reprezentuje jeho přechod do vodivostního pásu, k čemuž je zapotřebí energie Eg. Současně s přechodem elektronu do vodivostního pásu vznikne ve valenčním pásu díra. Vlastní vodivost polovodiče je tedy vždy realizována stejným počtem elektronů a děr.
Vliv příměsí donorového typu, které působí vodivost typu n, je zobrazen na obr. 7.26b. Energie donorových stavů leží zpravidla v zakázaném pásu velmi blízko "dna" vodivostního pásu. Elektrony lokalizované na donorových stavech mohou být tudíž uvolněny a převedeny do vodivostního pásu podstatně menší energií než Eg. Donorové příměsi přispívají tedy jen k elektronové vodivosti a vytvářejí polovodiče typu n.[61]
Konečně obr. 7.26c zobrazuje vliv akceptorových příměsí. Elektronové stavy lokalizované na akceptorech mají obvykle energie ležící v zakázaném pásu, a to velmi blízko "horního okraje" valenčního pásu. Relativně malá energie je tedy dostatečná k tomu, aby elektron byl lokalizován na akceptoru, čímž vznikne ve valenčním pásu díra. Akceptory tedy přispívají jen k děrové vodivosti a vytvářejí polovodiče typu p.


Mimořádně zajímavé a pro technické aplikace důležité vlastnosti má hraniční oblast rozdělující polovodiče typu p a typu n, nazývaná přechodem p-n. Všimněme si nyní jeho nejdůležitějších vlastností. Uvažujeme krystal, jehož jedna část je typu p a druhá typu n (viz obr. 7.27). V počátečním stadiu obsahuje volné elektrony pouze část n, zatímco díry obsahuje pouze část typu p. Obě části jsou elektricky neutrální, poněvadž volné elektrony kompenzují kladné náboje ionizovaných donorů a díry kompenzují záporné náboje ionizovaných akceptorů. Není však žádný důvod k předpokladu, že tento stav zůstane zachován. Naopak s ohledem na energetickou bilanci lze soudit, že (podobně jako v případě kovů - viz čl. 7.3.3) volné elektrony budou mít tendenci přecházet do části typu p a díry budou mít tendenci přecházet do části typu n. Tím se ovšem část typu n bude nabíjet kladně a část typu p záporně. Vzniklé elektrické pole EC bude bránit přechodu dalších nositelů, takže po určité době nastane rovnovážný stav. Tento stav bude charakterizován určitou koncentrací volných elektronů v části typu p a určitou koncentrací děr v části typu n (viz obr. 7.27a). Přesto však zůstanou za tohoto rovnovážného stavu elektrony hlavními (majoritními) nositeli proudu v části typu n a díry zůstanou majoritními nositeli proudu v části typu p.
Sledujme nyní vodivost přechodu. Přiložme zdroj vnějšího elektromotorického napětí E nejdříve kladným pólem k části typu p. Pak nastane situace podle obr. 7.27b. Vnější elektrické pole Ee se odečte od vlastního pole přechodu EC, takže další volné elektrony budou moci přecházet do části typu p a další díry do části typu n. Přechodem poteče proud. Říkáme, že vnější pole je k přechodu připojeno v propustném směru.
Přiložíme-li naopak vnější zdroj záporným pólem k části typu p, nastane situace znázorněném na obr. 7.27c. Pole zdroje se přičte k vnitřnímu poli přechodu, čímž budou díry vtahovány do části typu p a volné elektrony do části n. Oblast v okolí přechodu tak zůstane téměř bez nositelů proudu. Přechod p-n vede tudíž proud v tomto směru velmi špatně; říkáme, že vnější zdroj je připojen v nepropustném směru.


Na obrázku 7.28 je schematicky zobrazen průběh tzv. voltampérové charakteristiky přechodu p-n, což je závislost proudové hustoty j tekoucí přechodem na přiloženém napětí U. V propustném směru (A) může přechodem procházet značná proudová hustota již při napětí 0,1 V, zatímco v nepropustném směru (B) teče přechodem nepatrný proud do napětí 10 V. Zajímavý jev (tzv. Zenerův jev) nastane, dosáhne-li přiložené napětí v nepropustném směru určité kritické hodnoty UZ (Zenerovo napětí). Proud tekoucí přechodem počne při tomto napětí prudce vzrůstat, přičemž napětí na přechodu zůstává v podstatě konstantní na hodnotě UZ. Uvedený jev je způsoben tím, že dostatečně vysoké vnější elektrické pole může v oblasti p-n přechodu indukovat transport elektronů z valenčního do vodivostního pásu. Důsledkem je lavinovitý vzrůst koncentrace volných nositelů proudu se vrůstajícím napětím, čímž se zvyšuje vodivost přechodu.
Zmíněný lavinovitý vzrůst koncentrace volných nositelů proudu může být působen dvěma odlišnými mechanismy, které se uplatňují v různé míře u různých typů přechodu p-n. Za prvé může být průchod elektronů zakázaným pásem v oblasti přechodu p-n umožněn tzv. tunelovým jevem, který má čistě kvantově mechanickou povahu. Jeho uplatnění je v dané situaci podmíněno dostatečně vysokým spádem potenciálu na přechodu tak, aby horní okraj valenčního pásu v části p polovodiče byl na vyšší energii než dno vodivostního pásu v části n. Elektrony pak mohou tunelovat zakázaným pásem bez změny energie.
Druhý mechanismus spočívá v lavinovité ionizaci. Volní nositelé proudu realizující proud v nepropustném směru, interagují totiž s atomy v krystalu a při určité hodnotě elektrického pole získají energii potřebnou k jejich ionizaci, tj. k převedení dalších elektronů z valenčního do vodivostního pásu. Nehledě na různost fyzikální situace, může být tento způsob produkce volných nositelů proudu přirovnán k poměrům v plynu při nasazení doutnavého výboje (srov. čl 7.5.2).

Pokud je vhodnou konstrukcí přechodu zajištěn dostatečný odvod tepla vznikajícího průchodem značného proudu, a je tedy zamezeno nadměrnému zvýšení teploty přechodu, které by mohlo způsobit nevratné změny v jeho parametrech, vrátí se poměry v přechodu po snížení napětí do původního stavu. Přechod p-n může za uvedených podmínek pracovat i v oblasti Zenerova jevu.
Z obrázku 7.28 je vidět, že proud tekoucí přechodem p-n je složitou funkcí přiloženého napětí. Přechod p-n tedy není lineárním vodičem a neplatí pro něj Ohmův zákon. Specifické vlastnosti přechodu se využívají ke konstrukci rozmanitých elektronických prvků, které jsou základem moderní polovodičové elektroniky. Prvky obsahující jeden přechod p-n se nazývají diody. Jejich použití je mnohostranné. Na prvním místě je třeba jmenovat použití k usměrňovacím účelům, kdy se využívá nesymetrie voltampérové charakteristiky. (Usměrňované napětí musí ovšem být menší než napětí Zenerovo.) V současné době se k usměrňování používají zejména diody germaniové a křemíkové. Přechody p-n v křemíku mají v některých ohledech výhodnější vlastnosti (mimo jiné mohou pracovat při vyšší teplotě bez nebezpečí destrukce), a jsou proto pro usměrňovací účely používány téměř výhradně. Již na počátku tohoto článku bylo uvedeno, že vodivost polovodičů závisí značně na teplotě, neboť se změnou teploty může docházet k silným změnám koncentrace volných nositelů proudu. Snadno pochopíme, že podobný vliv mohou mít i další fyzikální podmínky, například osvětlení. Kvanta elektromagnetického záření (fotony) mohou totiž (podobně jako tepelné excitace) dodávat potřebnou energii pro tvorbu volných nositelů proudu. Víme, že vodivost přechodu p-n v nepropustném směru při osvětlení značně vzrůstá. Vhodně konstruované diody mohou být tudíž používány jednak jako detektory záření (fotodiody, fototranzistory), jednak jako optoelektronické zdroje světla (elektroluminiscenční diody, polovodičové lasery).
Vedle prvků s jedním přechodem p-n je možné konstruovat i složitější prvky obsahující větší počet přechodů. Podstatná je přitom skutečnost, že při vhodné konstrukci je možné dosáhnout vzájemného ovlivňování jednotlivých přechodů prvku, čímž vznikají kvalitativně nové možnosti využití. Historicky první a patrně nejvýznamnější je objev tranzistorového jevu a na něm založeného prvku - tranzistoru, který je tvořen polovodičovým krystalem, jehož krajní části jeví vodivost jednoho typu a střední část jeví vodivost druhého typu. Jednotlivé části jsou odděleny přechody p-n, takže tranzistor představuje vlastně dvojici diod, které se vzájemně ovlivňují.
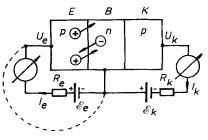
Na obrázku 7.29 je schematicky zobrazen tranzistor, jehož střední část je typu n. (Tento typ tranzistoru se nazývá PNP; tranzistor, jehož střední část je typu p, se nazývá NPN). K jednotlivým oblastem krystalu jsou připojeny elektrody nazývané obvykle emitor E, báze B, kolektor K.
Podle obr. 7.29 budeme kvalitativně sledovat možnost vzájemného ovlivňování obou přechodů, tj. situaci, kdy proud tekoucí jedním z nich ovlivňuje proud v druhém přechodu. Mezi bázi a kolektor připojíme zdroj elektromotorického napětí E k polarizovaný v nepropustném směru a v obvodu emitoru nahradíme na chvíli zdroj E e krátkým spojením s bází (čárkovaný spoj na obrázku). V přechodu p-n mezi kolektorem a bází nastane situace, kterou vidíme na obr. 7.27c. Přechod bude zbaven téměř všech nositelů proudu a obvodem kolektoru nepo-teče téměř žádný proud. Rozpojíme-li nyní krátké spojení mezi bází a emitorem a připojíme-li k emitoru zdroj E e polarizovaný v propustném směru, počne přechodem emitor-báze protékat proud. V tomto přechodu nastane situace zobrazená na obr. 7.27b, do střední části vodiče počnou proudit díry, jak je schematicky naznačeno na obr. 7.29. Za předpokladu, že střední část krystalu je dostatečně tenká, mohou tyto díry difundovat k přechodu kolektor-báze. Tím se v něm poruší rovnovážný stav a kolektorem počne protékat proud.

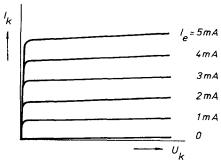
Na obrázku 7.30 jsou uvedeny tzv. kolektorové charakteristiky tranzistoru, které udávají závislost kolektorového proudu Ik na kolektorovém napětí Uk pro různé hodnoty proudu emitorového Ie . Vidíme, že každá křivka vlastně představuje charakteristiku diody v nepropustném směru (samozřejmě pro Uk < UZ ); nasycené proudy různých křivek však rostou se vzrůstem proudu Ie . Při dané hodnotě Uk kolektorového napětí je tedy kolektorový proud funkcí proudu emitorového. (Obráceně, jelikož proud v emitorovém obvodu je ovlivňován proudem kolektorovým, je možné konstruovat i emitorové charakteristiky udávající závislost emitorového proudu Ie na emitorovém napětí Ue pro různé hodnoty proudu kolektorového. Podrobněji ještě o chování tranzistoru v obvodech pojednáme v odst. 8.3.3b.)
Vhodnou konstrukcí tranzistoru lze dosáhnout toho, že malým emitorovým výkonem lze regulovat značné výkony kolektoru. Je proto možné využívat tranzistoru jako zesilovacího prvku. Vedle uvedených prvků, jako je dioda a tranzistor, je možné vlastnosti polovodičů a zejména vlastnosti přechodu p-n využívat pro konstrukci řady dalších prvků různých vlastností a kromě toho je možné využívat různé technologie přípravy p-n přechodu, čímž vznikají prvky rozdílných parametrů. Rozvoj polovodičové technologie umožňuje navíc zmenšovat rozměry jednotlivých prvků a sdružovat je ve značném počtu do integrovaných funkčních celků, které jsou při malých rozměrech a malé spotřebě energie schopné vykonávat velmi složité operace.
Kvalitativním skokem v uvedeném procesu znamenalo zavedení technologie epitaxní přípravy dokonalých polovodičových vrstev, která umožnila zhotovit tzv. heteropřechody (čímž se rozumí technologie přípravy dokonalého spojení dvou různých polovodičů) či heterostruktury (čímž se rozumí příprava několika heteropřechodů za sebou). Tato technologie znamenala nejen kvalitativní skok v procesu miniaturizace a integrace polovodičových součástek, ale také kvalitativní skok v parametrech různých typů součástek; především vysokofrekvenčních tranzistorů, polovodičových detektorů záření, slunečních fotovoltaických článků, eletroluminiscenčních diod a polovodičových laserů.
Vlastnosti polovodičů a vlastnosti přechodu p-n se tak staly základem pro bouřlivý rozvoj elektroniky a výpočetní techniky v posledních desetiletích. Objev tranzistorového jevu je z tohoto hlediska možné považovat za jeden z nejvýznamnějších objevů fyziky 20. století. Podrobnější výklad o vlastnostech, konstrukci a použití jednotlivých typů polovodičových prvků přesahuje možnosti této učebnice. Některá nejjednodušší použití v nelineárních obvodech budou ještě vysvětlíme v kapitole 8. Pro další poučení, zejména o klasických metodách měření parametrů polovodičových prvků, odkazujeme na učebnici [5] a dále na speciálnější technickou literaturu.[62]
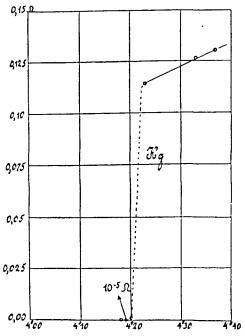
Supravodivost objevil holandský fyzik H. Kammerling-Onnes v roce 1911 krátce po tom, co se mu podařilo zkapalnit helium, čímž byly vytvořeny předpoklady pro studium vlastností látek při nízkých teplotách. Kammerling-Onnes studoval teplotní závislost elektrického odporu rtuti. Zatímco při vyšších teplotách se odpor choval obvyklým způsobem (srov. obr. 7.19), přibližně při teplotě 4,2 K klesla náhle jeho hodnota téměř na nulu. Obrázek 7.31 ukazuje autentické výsledky jeho měření.[63]
Později byla supravodivost nalezena u řady dalších látek kovového charakteru; v současné době je supravodivost známa u 26 prvků za normálního tlaku a u několika dalších za zvýšeného tlaku, kromě toho je známo mnoho set supravodivých slitin a sloučenin. Téměř nulová hodnota elektrického měrného odporu při teplotách nižších než jistá kritická teplota Tc však není jedinou významnou vlastností supravodivého stavu. Stejně významné a anomální je chování supravodičů v magnetickém poli.
Bylo zjištěno, že supravodivý stav při dané teplotě může být zrušen vnějším magnetickým polem, a rovněž, že kritická teplota Tc na magnetickém poli závisí. Při zvyšování magnetického pole kritická teplota Tc klesá. Překročí-li magnetické pole určitou, pro danou látku charakteristickou, hodnotu, látka nepřejde do supravodivého stavu při sebenižší teplotě. Dále bylo zjištěno, že supravodivost prvků je zpravidla zrušena již relativně nízkým magnetickým polem, zatímco u některých slitin a intermetalických sloučenin supravodivost existuje i do znač-ně vysokých polí. Oba typy látek v supravodivém stavu přitom mají různé magnetické vlastnosti. Typ supravodivosti vyskytující se u prvků se nazývá supravodivostí I. typu, supravodivost sloučenin a slitin, která se zachová i ve vysokých polích, se nazývá supravodivostí II. typu.



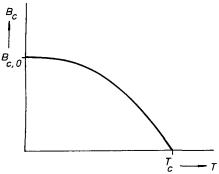
Obrázek 7.32 ukazuje teplotní závislost kritického pole Bc, při kterém látka přechází do normálního stavu, pro supravodiče I. typu. V poli vyšším než Bc,0 nepřejde látka do supravodivého stavu při žádné teplotě. Další důležitou vlastností supravodičů I. typu je platnost tzv. Meissnerova-Ochsenfeldova jevu, podle něhož je v supravodiči dostatečně velkých rozměrů[64] za každých okolností magnetická indukce nulová, tj. B = 0.
Na první pohled by se mohlo zdát, že nulovost magnetické indukce je důsledkem zákona elektromagnetické indukce v prostředí o nulovém měrném odporu. Skutečně, z Ohmova zákona E = ρ R j vyplývá, že v prostředí s nulovým měrným odporem (ρ R = 0) musí být za předpokladu konečné proudové hustoty všude E = 0 a z Maxwellovy rovnice (5.5) dostáváme
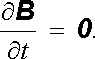 |
Je-li tedy v počátečním stavu všude B = 0 , musí magnetická indukce zůstat nulová i nadále; při libovolných změnách vnějšího magnetického pole tyto změny indukují v supravodiči elektrický proud, který podle Lenzova pravidla vnější pole kompenzuje.
Zákon elektromagnetické indukce se však netýká situace, kdy je vzorek ochlazován pod kritickou teplotu v konstantním nenulovém magnetickém poli. V normálním stavu je i ve vzorku nenulová magnetická indukce, při ochlazení pod kritickou teplotu (a tedy při přechodu do supravodivého stavu) by zákon elektromagnetické indukce připouštěl rovněž nenulové pole uvnitř vzorku. Experiment však ukazuje, že i v takové situaci je při přechodu do supravodivého stavu magnetické pole z objemu vzorku vytlačeno. Pro supravodiče I. typu je tedy supravodivý stav charakterizován dvěma nezávislými podmínkami:
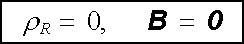 |
(7.32) |
v celém objemu (s výjimkou velmi tenké povrchové vrstvy).
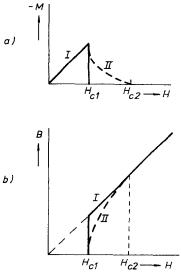
Z podmínky B = 0 pro supravodič I. typu vyplývá M = -H . Látka se tedy chová jako "ideální diamagnetikum" s hodnotou magnetické susceptibility χ m = -1. Plné křivky na obr. 7.33 ukazují průběh magnetizace M a magnetické indukce v supravodiči I. typu, který již při poli Hc,1 přechází skokem do normálního stavu. Jiné chování jeví supravodiče II. typu. U těchto látek existuje ještě interval magnetických potí (Hc,1, Hc,2), v němž má látka téměř nulový měrný odpor, magnetická indukce v supravodiči však již nemusí být nulová. Její hodnota postupně vzrůstá a magnetizace klesá, až při kritickém poli Hc,2 přejde vzorek do normálního stavu.
Podrobnější studium vlastností supravodičů II. typu ukázalo, že v intervalu polí (Hc,1, Hc,2) není v supravodivém stavu celý objem vzorku. Magnetické pole vniká do vzorku jen v určitých vláknech, která jsou v normálním stavu a jsou obklopena supravodivým prostředím, jež vlastně způsobuje nulový elektrický odpor. Objem látky v supravodivém stavu se při vzrůstajícím poli zmenšuje a při poli Hc,2 se stává nulovým. Elektrický odpor v tomto okamžiku vzroste na normální hodnotu.

Díky tomu, že supravodivý stav v supravodičích II. typu může existovat do značně vysokých magnetických polí, mají především tyto látky technický význam pro vedení velkých proudů bez ztrát jouleovým teplem. V nejlepších dosud připravených kovových supravodičích může proudová hustota dosahovat hodnot v řádu 109 A.m-2, což je přibližně o tři řády více, než je možné v nor-málních vodičích.
Tabulka 7.9 Kritické teploty a kritické pole vybraných supravodičů
|
prvky (supravodiče I. typu) |
sloučeniny, slitiny (supravodiče II. typu) |
||||
|
látka |
Tc (K) |
Bc (T) |
látka |
Tc (K) |
Bc (T) |
|
rtuť (Hg) hliník (Al) olovo (Pb) cín (Sn) kadmiu (Cd) vanad (V) zinek (Zn) niob (Nb) |
4,154 1,175 7,196 3,722 0,517 5,40 0,85 9,25 |
4,11 . 10-2 1,04 . 10-2 8,03 . 10-2 3,05 . 10-2 2,80 . 10-3 1,41 . 10-1 5,30 . 10-3 2,06 . 10-1 |
Nb3Sn Nb3Al Nb3Al0,75Ge0,25 Nb3Ge Nb-Zr Nb-Ti |
18-18,3 18,7 18,5 23,2 9-11 8-10 |
22,5-23,5 29,5 42
6-9 9-12 |
V tabulce 7.9 jsou pro ilustraci uvedeny kritické teploty a kritická pole pro několik kovových supravodičů I. a II. typu. Rekordní kritická teplota Tc = 23,2 K, která je již nad bodem varu vodíku (20,4 K), byla u těchto supravodičů dosažena v případě Nb3Ge.
V roce 1986 objevili pracovníci laboratoří firmy IBM v Curichu K. A. Müller a J. G. Bednorz jistý druh supravodivosti u látek zcela jiného typu, a to u ke-ramických materiálů se strukturou minerálů zvaných perovskity. Kritické teploty některých těchto látek bohatě přesahují bod varu dusíku (77,3 K); například u materiálu o složení HgBa2Ca2Cu3O8 byla spolehlivě prokázána kritická teplota 134 K. Experimenty ukazují že jde o supravodiče II. typu, jejichž kritické pole Hc,2 i kritická hustota supravodivého proudu mohou dosahovat značně vysokých hodnot. V případě, že by se podařilo připravit dobře technicky využitelné mate-riály tohoto typu, mohl by zmíněný objev, dnes běžně nazývaný vysokoteplotní supravodivost, způsobit revoluci v mnoha odvětvích techniky. Více než dese-tiletý intenzivní výzkum však dosud nevedl k jeho významnějšímu praktickému uplatnění.
Plného pochopení fyzikální podstaty supravodivého stavu klasických kovových supravodičů bylo dosaženo až téměř za půl století po jeho objevu. V třicátých letech byla vypracována Londonova fenomenologická teorie, reprezentovaná tzv. Londonovými rovnicemi, jež dovolují fenomenologický popis chování supravodičů I. typu. Pozdější Ginzburgova-Landauova teorie umožnila vysvětlit i chování supravodičů II. typu, plné pochopení podstaty supravodivosti však přinesla teprve kvantová mikroskopická teorie, kterou v roce 1957 vypracovali J. Bardeen, L. N. Cooper a J. R. Schriffer. Takzvaná BCS teorie patří bezesporu k největším úspěchům teoretické fyziky 20. století.
Podstatou supravodivosti je vznik dvojic vzájemně vázaných vodivostních elektronů, tzv. Cooperových párů, které se mohou v kovu tvořit při dostatečně nízkých teplotách díky elektrické interakci elektronů s krystalovou mřížkou. Elektrická interakce vodivostniho elektronu s krystalovou mřížkou může totiž v jeho okolí ovlivnit spektrum kmitů krystalové mřížky, čímž může vzniknout energeticky výhodná situace pro zachycení jiného vodivostniho elektronu s opačným momentem hybnosti. Energie vazby elektronů v tomto páru je velmi malá; řádu 10- 4 eV. Přesto se mohou oba elektrony v krystalu korelovaně pohybovat, přičemž je podstatné, že pár jako celek má nulový vlastní moment hybnosti, takže pro něj neplatí Pauliho princip a korelace zůstává zachována na vzdálenostech mnohem větších, než je mřížková konstanta krystalu. Nehomogenity v periodicitě krystalové mřížky pak přestanou znatelně ovlivňovat pohyb elektronů vázaných v Cooperových párech.
Párování nositelů proudu do útvarů s nulovým vlastním momentem hybnosti je nepochybně základní podmínkou pro vznik jakékoliv supravodivosti. Dnes je však již zřejmé, teorie BCS ve své klasické podobě není schopna vyložit vysokoteplotní supravodivost.
V roce 1962 předpověděl B. Josephson, že korelace v pohybu elektronů může zůstat zachována i v případě, kdy dvě části supravodiče jsou odděleny tenkou vrstvou nevodiče. Předpověděl tak existenci jevů, dnes nazývaných Josephsonovými jevy (respektive slabou supravodivostí), na jejichž základě vznikly nové měřicí metody elektrického napětí a magnetického toku, které umožnily o mnoho řádů zvýšit citlivost a přesnost měření těchto veličin ve srovnání s metodami tradičními.[65]
Experimentální zkušenost ukazuje, že za určitých podmínek mohou z povrchu kovů (ale i polovodičů) vystupovat volné elektrony. Podmínkou pro vznik tohoto jevu, který se nazývá elektronová emise, je získání dostatečně vysoké energie. Tato energie bude zřejmě dána rozdílem mezi energií volného elektronu ve vakuu a energií volných elektronů v látce, která může být v prvním přiblížení charakterizována polohou Fermiho hladiny. Podle obr. 7.25 v článku 7.3.3 je tato energie rovna eφ a nazývá se výstupní prací.
Existuje několik mechanismů jak získat energii potřebnou pro uvolnění elektronu z pevné látky. Podle typu tohoto mechanismu rozeznáváme různé druhy elektronové emise:
Termickou emisi (termoemisi), která nastává při dostatečném zvýšení teploty dané látky, kdy je dostatečný počet elektronů excitován tepelným pohybem.
Fotoemisi vznikající při ozáření látky elektromagnetickým, především krátkovlnným (viditelným, ultrafialovým, rentgenovým) zářením. Potřebná energie je elektronům dodávána interakcí s fotony.
Autoemisi, ta zahrnuje "vytrhování" volných elektronů z látky vnějším magnetickým polem. Vzniká při přiložení elektrického pole dostatečné intenzity k povrchu látky. (Efekt je obvykle pozorovatelný při intenzitách vyšších než 107 V.m-1.)
Sekundární emisi, jež je vyvolána dopadem dostatečně rychlých elektronů (eventuálně jiných hmotných částic) na povrch sledované látky; tyto částice pak mohou předat svoji energii elektronům ve vodivostním pásu.


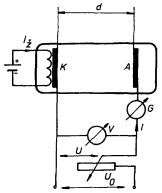
Všechny uvedené typy emise elektronů mají v dnešní době své uplatnění v různých technických aplikacích. Jelikož se však nejčastěji setkáme s termo-emisí a fotoemisí, všimneme si jejich vlastností poněkud podrobněji. Termoemisi lze pozorovat v uspořádání, které je schematicky znázorněno na obr. 7.34. V evakuované baňce jsou umístěny dvě elektrody. Elektroda K (zvaná katoda), která je zhotovena z materiálu, jehož emisi zkoumáme, je připojena k zápor-nému pólu zdroje napětí U0. Druhá elektroda A (anoda) je přes vhodný přístroj (klasicky přes galvanometr) umožňující měřit emisní proud připojena k jeho kladnému pólu. Katoda je udržována na žádoucí teplotě T, například prostřednictvím tepelného kontaktu s topnou spirálou vytápěnou pomocným proudem Iz. Pro jednoduchost předpokládáme, že obě elektrody jsou rovinné, mají plochu S a jsou vzájemně rovnoběžné.

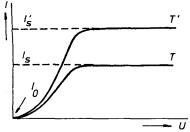
Budeme-li v popsaném uspořádání měřit při dané konstantní teplotě katody závislost emisního proudu I na přiloženém napětí U, dostaneme závislost uvedenou na obr. 7.35. Proud, jehož hodnota není zcela nulová při U = 0, bude se vzrůstajícím napětím nejdříve vzrůstat a po dosažení určité nasycené hodnoty Is nebude již dále na napětí závislý. Hodnota proudu v nenasycené oblasti není určena vlastnostmi materiálu katody. Zákonitosti určující jeho průběh v závislosti na napětí budeme studovat v následujícím článku. Nasycená hodnota protékajícího proudu je naopak určena materiálem katody a její teplotou. Při zvýšení teploty katody na hodnotu T ℜ' naměříme novou křivku podobného průběhu s vyšší hodnotou nasyceného proudu.
Vlastnosti nasyceného emisního proudu lze popsat tzv. Richardsonovým-Dushmanovým vztahem, který lze odvodit na základě modelu elektronového plynu, pro jehož rozdělení energie použijeme Fermiho-Diracovo rozdělení. Pak je možné vypočítat četnost elektronů ve vodivostním pásu, které mají dostatečnou energii pro opuštění látky, a tedy i hustotu emisního proudu. Richardsonův-Dushmanův vztah vyjadřuje hustotu nasyceného emisního proudu js jako funkci teploty T a výstupní práce eφ daného materiálu. Platí
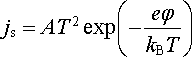 , , |
(7.33) |
kde kB je Boltzmannova konstanta. Pro veličinu A vyplývá z teorie, že by měla být téměř stejná pro všechny látky a blízká hodnotě 1,2.106 A.m-2.K-2. Ve skutečnosti je však nutné ji určovat pro jednotlivé látky experimentálně z naměřené teplotní závislosti emisního proudu.
Fotoemisi lze pozorovat v principiálně stejném uspořádání. Katoda, která je zdrojem emitovaných elektronů (srov. obr. 7.34), není ovšem žhavena, musí však být uzpůsobena tak, aby bylo možné její povrch přilehlý k anodě ozařovat žádaným elektromagnetickým zářením. Pro vyšetřování vlastností fotoemise je rovněž žádoucí možnost změny polarity napětí zdroje U0.
Při kladné polaritě anody vůči katodě, tj. ve stejném uspořádání jako při měření napěťové závislosti emisního proudu termoemise, bude mít napěťová závislost emisního proudu (při konstantní intenzitě záření) kvalitativně stejný průběh jako v případě termoemise (srov. obr. 7.35); hodnota nasyceného emisního proudu bude přitom vzrůstat s rostoucí intenzitou záření dopadajícího na katodu.
Velmi zajímavé a důležité je studium závislosti emisního proudu na vlnové délce a frekvenci dopadajícího záření, tj. měření napěťové závislosti emisního proudu při osvětlení monochromatickým zářením. Při měření především zjistíme, že při záření o větší vlnové délce, než je jistá kritická hodnota λ 0 = c/v0, v0 = ω 0/2π , fotoemise vůbec nenastává. Další zajímavou vlastnost lze zjistit měřením napěťové závislosti emisního proudu v opačné polaritě (tj. s kladným pólem zdroje připojeným k fotokatodě a záporným pólem připojeným k anodě); s rostoucím napětím proud klesá, přičemž klesne na nulu při určité hodnotě napětí závislé na vlnové délce (frekvenci) použitého záření. Budeme-li měřit Ug,ω pro záření různých vlnových délek, zjistíme přímou úměrnost mezi Ug,λ a ω .
Uvedené vlastnosti fotoemise lze snadno vysvětlit pomocí předpokladu, že dopadající foton předá veškerou svoji energii Ef = hω emitovanému elektronu. Předpokládáme-li dále zachování energie při srážce fotonu s elektronem, dostaneme pro energetickou bilanci podmínku (Einsteinův vztah)
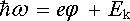 , , |
(7.34) |
podle níž se předaná energie spotřebuje na výstupní práci a zbytek bude tvořit kinetickou energii Ek = mev 2/2 emitovaného elektronu. Podle podmínky (7.34) je pak zřejmé, že fotony o energii menší než výstupní práce hω < eφ nemohou emisi vyvolat. Fotoemise nastává při prahové frekvenci ω 0
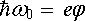 . . |
(7.35) |
Při nulovém nebo malém záporném napětí mezi katodou a anodou teče obvodem jistý emisní proud díky nenulové kinetické energii emitovaných elektronů. Proud klesne na nulu, budou-li emitované elektrony zcela zbržděny přiloženým napětím, tj. bude-li platit Ek = eUg,ω . Z (7.34) lze potom získal závislost Uk,ω na frekvenci ω
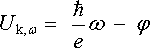 . . |
(7.36) |
Vidíme, že závislost je skutečně lineární. Na základě měření Uk,ω pro několik frekvencí lze z (7.36) určit poměr h/e a i výstupní práci použitého materiálu katody.
Jev elektronové emise se stal základem klasické vakuové elektroniky, která si přes bouřlivý rozvoj polovodičové elektroniky stále zachovává svůj význam. Kromě toho v historii fyziky jev elektronové emise významně přispěl k rozvoji poznání mikrostruktury látek a k formulování základních postulátů kvantové mechaniky. Speciálně termoemise i fotoemise dávají dobré možnosti pro měření výstupní práce elektronů v různých typech látek. V tabulce 7.10 jsou pro informaci uvedeny některé hodnoty získané oběma metodami.
Tabulka 7.10 Výstupní práce elektronů některých kovů
|
termoemise |
fotoemise |
||
|
emitující látka |
eφ (eV) |
emitující látka |
eφ (eV) |
|
Ag Cs Ni Pt Ta W |
4,8 2,1 4,6 5,3 4,2 4,5 |
Ag Al Cs Ni Ta W |
4,3 4,2 1,8 5,0 4,1 4,5 |
Nyní obrátíme pozornost na studium zákonitostí emisního proudu v nena-syceném stavu. V předchozím článku jsme viděli, že zatímco nasycený emisní proud je dán výhradně emisními schopnostmi katody, proud při nižších napětích je zřejmě dán podmínkami jiného druhu. Pro nalezení těchto podmínek se vrátíme k experimentálnímu uspořádání podle obr. 7.34, s kladnou polaritou zdroje na anodě.
Uspořádání s rovinnými elektrodami umožňuje řešit úlohu jako rovinný problém. Položme osy y, z souřadné soustavy do roviny katody a osu x volme tak, aby její kladný směr mířil k anodě. V ustáleném stavu, kdy obvodem teče stacionární proud, musí vzhledem k rovnici kontinuity proudu existovat i v prostoru mezi elektrodami stacionární rozložení hustoty konvekčního proudu. Jelikož záporně nabité elektrony proudí od katody k anodě, platí pro ni j ℜ ≡ (-j, 0, 0), j = | j | > 0. Podle (3.11) je možné hustotu j vyjádřit pomocí rychlosti elektronů v a pomocí objemové hustoty jejich náboje ρ ; j = ρ v . Obecně je nutné předpokládat, že obě tyto veličiny jsou funkcí souřadnice x.
V prostoru mezi katodou a anodou existuje elektrické pole, které je dáno jednak napětím U přiloženým na elektrody, jednak prostorovým rozložením elektronů. Potenciál tohoto pole je rovněž funkcí souřadnice x a musí vyhovovat Poissonově rovnici
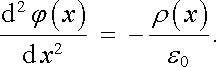 |
(7.37) |
Předpokládejme, že elektrony vystupují z katody s nulovou
rychlostí, takže platí v
(0) = 0.
Ve vzdálenosti x od katody bude
jejich rychlost v
(x)
určena rovností mezi potenciální a kinetickou energií. Budeme-li povrch katody
považovat za hladinu o nulovém potenciálu φ
(0)
= 0,
můžeme napsat v
(
x
)
=
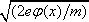 .
Po dosazení do
(7.37)
dostaneme pro potenciál diferenciální rovnici
.
Po dosazení do
(7.37)
dostaneme pro potenciál diferenciální rovnici
 |
(7.38) |
Jelikož jde o
diferenciální rovnici druhého řádu, je nutné pro nalezení jejího partikulárního
řešení předepsat okrajovou podmínku nejen pro hodnotu potenciálu, ale také pro
hodnotu jeho derivace. Kromě φ
(0)
= 0
budeme požadovat
 (později tuto podmínku fyzikálně zdůvodníme).
Potom, vynásobíme-li rovnici
(7.38)
derivací d
φ
/dx
, můžeme její první integrál psát ve
tvaru
(později tuto podmínku fyzikálně zdůvodníme).
Potom, vynásobíme-li rovnici
(7.38)
derivací d
φ
/dx
, můžeme její první integrál psát ve
tvaru
 |
(7.39) |
Tuto rovnici lze již integrovat separací proměnných
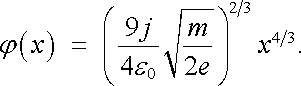 |
(7.40) |
Speciálně pro x = d platí φ (d) = U a
 |
(7.41) |
Proudová hustota j, a tedy i proud v obvodu jsou úměrné U3/2.
Tento výsledek, zvaný někdy Langmuirův
třípolovinový vztah, platí ovšem pouze za předpokladu, že je splněna
podmínka
 ,
která požaduje nulovost intenzity pole povrchu katody. Podmínka může být
zřejmě splněna pouze za předpokladu, že v prostoru mezi anodou a katodou
existuje prostorový náboj elektronů dostatečné velké hustoty ρ
(x)
. (Kdyby tento náboj neexistoval, bylo
by v celém prostoru mezi elektrodami homogenní pole o intenzitě E0 = U/d.)
Je dokonce nutné, aby se vzrůstající hodnotou přiloženého napětí hustota
prostorového náboje v daném bodě vzrůstala. To je však možné jen tehdy,
je-li proud tekoucí obvodem menší než emisní schopnost katody, tj. menší než
nasycený proud Is.
,
která požaduje nulovost intenzity pole povrchu katody. Podmínka může být
zřejmě splněna pouze za předpokladu, že v prostoru mezi anodou a katodou
existuje prostorový náboj elektronů dostatečné velké hustoty ρ
(x)
. (Kdyby tento náboj neexistoval, bylo
by v celém prostoru mezi elektrodami homogenní pole o intenzitě E0 = U/d.)
Je dokonce nutné, aby se vzrůstající hodnotou přiloženého napětí hustota
prostorového náboje v daném bodě vzrůstala. To je však možné jen tehdy,
je-li proud tekoucí obvodem menší než emisní schopnost katody, tj. menší než
nasycený proud Is.
Podmínka
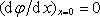 vyjadřuje rovnovážný stav mezi elektrony
uvnitř katody a elektronovým oblakem v prostoru mezi katodou a anodou. Je nutná
pro existenci stacionárního proudu. Kdyby totiž při dané hustotě proudu j bylo
vyjadřuje rovnovážný stav mezi elektrony
uvnitř katody a elektronovým oblakem v prostoru mezi katodou a anodou. Je nutná
pro existenci stacionárního proudu. Kdyby totiž při dané hustotě proudu j bylo
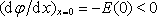 ,
elektrony, které podle předpokladu vystupují z katody s nulovou rychlostí, by
tímto polem byly vráceny zpět na katodu a proud obvodem by musel nutně klesat.
Obráceně, kdyby platilo
,
elektrony, které podle předpokladu vystupují z katody s nulovou rychlostí, by
tímto polem byly vráceny zpět na katodu a proud obvodem by musel nutně klesat.
Obráceně, kdyby platilo
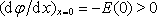 ,
byly by z katody odváděny další elektrony a proud obvodem by stoupal tak
dlouho, dokud by se plně nevyužilo emisní schopnosti katody.
,
byly by z katody odváděny další elektrony a proud obvodem by stoupal tak
dlouho, dokud by se plně nevyužilo emisní schopnosti katody.
Uspořádání podle obr. 7.34 reprezentuje vlastně nejjednodušší typ elektronky (diody), která se, jak známo, nejčastěji užívala k usměrňování střídavého napětí. Zařazením dalších elektrod do blízkosti katody je možné získat další typy elektronek. Například umístíme-li do blízkosti katody jednu elektrodu (tzv. mřížku) ve tvaru kovové síťky, která umožňuje průlet elektronů, získáme triodu. Napětím přivedeným z vnějšího zdroje na mřížku lze řídit prostorový náboj elektronů, a tedy i proud elektronkou. Tvar charakteristik uvedený na obr. 7.35 bude tedy v nenasyceném stavu záviset na napětí mřížky. Vzhledem k tomu, že malými změnami mřížkového napětí je možné získat značné změny proudu elektronkou, je elektronku možné použít například k zesilování malých časově proměnných napětí.