V kapitolách l a 3 jsme ukázali, že vliv látkového prostředí na elektrické a magnetické pole je popsán vektory elektrické polarizace P e( r ) a magnetické polarizace P m( r ) (respektive magnetizace M ( r ) ), jejichž hodnoty jsou závislé na intenzitách příslušných polí v daném látkovém prostředí. Dále jsme poznali, že pro dosti velké množství látek je možné tuto závislost dobře aproximovat lineárními vztahy mezi okamžitými hodnotami uvedených veličin, čímž jsou definovány tzv. materiálové konstanty - elektrická a magnetická susceptibilita, respektive permitivita a permeabilita.
Uvedené definiční vztahy pro elektrickou susceptibilitu χ e, respektive permitivitu ε (1.255) , (1.259) a pro magnetickou susceptibilitu χ m, respektive permeabilitu μ (3.140) až (3.142) jsou zcela analogické. Uvidíme dále, že určité analogie jsou i ve vlastnostech elektrických a magnetických materiálových konstant, i když v původu elektrických a magnetických momentů atomů a molekul jsou podstatné rozdíly (srov. článek 7.1.4). Na druhé straně však jsou tyto vlastnosti v mnohém rozdílné. Pro zdůraznění podobnosti i rozdílů jsou dielektrické a magnetické vlastnosti jednotlivých typů látek vykládány ve vzájemné návaznosti v jednotlivých článcích tohoto oddílu.
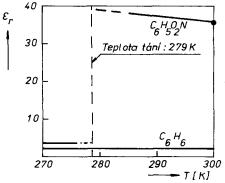
Tabulka 7.3 uvádí příklady experimentálních hodnot statické relativní permitivity ε r lineárních dielektrik různého skupenství [11]. Jak je vidět z tabulky, mění se její hodnoty pro jednotlivé typy látek v širokém rozmezí. Relativní permitivita plynů je jen nepatrně větší než jedna, což zřejmě souvisí s malým počtem molekul v jednotce objemu ve srovnání s látkami v kondenzovaném stavu. Velké hodnoty permitivity se nejčastěji vyskytují u kapalin, u nichž v některých případech dosahuje její hodnota několika desítek. V případě pevných lineárních dielektrik naopak jen zřídka přesahuje hodnotu deseti. Obrázek 7.8 demonstruje různý charakter chování permitivity při změně skupenství benzenu C6H6 a nitrobenzenu C6H5O2N. Obě látky mají téměř stejnou teplotu tání. Avšak zatímco v případě benzenu se permitivita nijak nemění, v případě nitrobenzenu několikanásobně vzrůstá.
Tabulka 7.3 Permitivita vybraných látek při pokojové teplotě
|
skupenství |
látka |
teplota (K) |
relativní permitivita r
|
|
plyny při tlaku 101,3kPa |
dusík N2 helium He kyslík O2 |
300 300 300 |
1,000 528 1,000 066 1,000 486 |
|
kapaliny |
aceton (C3H6O) benzen (C6H6) etylalkohol (C2H6O) chloroform (CHCl3) toluen (C7H8) nitrobenzen (C6H5O2N) voda (H2O) |
295
295 |
21,4 2,284 25,1 4,8 2,38 35,72 81 |
|
pevné látky |
diamant (C) kamenná sůl (NaCl) jantar korund polystyren trolitul tetrafluoretylen skla |
295
295 |
13,1 5,9 2,8 10 2,4 2,53 2,12 3,7 ÷ 7 |
Pro pochopení mechanismů polarizace látek má velký význam studium te-plotní závislosti permitivity. V případě lineárních dielektrik lze tuto závislost obvykle dobře vyjádřit vztahem
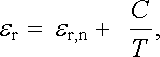 |
(7.12) |

ve kterém T je absolutní teplota a ε r,n, C teplotně nezávislé konstanty. Permitivita tedy jeví přímkovou závislost ve tvaru 1/T, jak pro některé látky demonstruje obr. 7.9. Jednotlivé členy na pravé straně (7.12) zřejmě souvisí s různými mechanismy polarizace. Jak obrázek dále ukazuje, látky s nízkou celkovou hodnotou permitivity vykazují rovněž malou závislost na teplotě.

 Jak bylo již řečeno v čl. 1.5.4, krystaly s
jinou než kubickou symetrií mohou být dielektricky anizotropní. Elektrická
susceptibilita (respektive permitivita) je symetrický tenzor druhého řádu
(srov. vztah
(1.261)
). Pro úplný popis chování takových látek v elektrickém
poli je zapotřebí obecně udat tři hlavní hodnoty tenzoru permitivity; v případě
struktur s osovou symetrií jsou dvě hlavní hodnoty stejné, takže se počet
potřebných údajů redukuje na dva. Například krystal korundu Al2O3,
s trigonální symetrií, má hlavní hodnoty permitivity ε
r,c = 11,54,
ε
r,a = ε
r,b = 9,34.
Jak bylo již řečeno v čl. 1.5.4, krystaly s
jinou než kubickou symetrií mohou být dielektricky anizotropní. Elektrická
susceptibilita (respektive permitivita) je symetrický tenzor druhého řádu
(srov. vztah
(1.261)
). Pro úplný popis chování takových látek v elektrickém
poli je zapotřebí obecně udat tři hlavní hodnoty tenzoru permitivity; v případě
struktur s osovou symetrií jsou dvě hlavní hodnoty stejné, takže se počet
potřebných údajů redukuje na dva. Například krystal korundu Al2O3,
s trigonální symetrií, má hlavní hodnoty permitivity ε
r,c = 11,54,
ε
r,a = ε
r,b = 9,34.
Elektrická susceptibilita a permitivita byly zavedeny v kapitole l pro popis chování látek ve statickém poli. Pro popis časově proměnného elektrického pole v lineárním dielektriku je však třeba zkoumat i vlastnosti dielektrika v závislosti na rychlosti časových změn pole. Nejčastěji užívaným postupem je studium chování dielektrik ve střídavém poli v závislosti na jeho frekvenci. Z měření tohoto druhu pak získáme frekvenční spektrum permitivity, respektive elektrické susceptibility. U látek s vysokou statickou permitivitou klesá zpravidla její hodnota již při relativně nízkých frekvencích. Například statická permitivita vody je ε r,s = 81; při frekvenci ~1010 Hz však již značně klesá a při velmi vysokých (například optických) frekvencích má permitivitu ε r,ℜ nekonecno = 1,77. Podobně kamenná sůl (NaCl) má statickou permitivitu ε r,s = 5,9, zatímco při velmi vysokých frekvencích ε r,ℜ nekonecno = 2,25. Naproti tomu tetrafluoretylen má relativní permitivitu ε r = 2,12 téměř frekvenčně nezávislou až do velmi vysokých frekvencí. Důležité je, že v oborech se silnou frekvenční závislostí permitivity nastávají při periodickém přepolarizování ztráty energie, kterou musí dodávat zdroje elektrického pole.


Malou co do počtu, ale důležitou skupinu dielektrik tvoří tzv. feroelektrické látky. Pro ně je charakteristický anomální vztah mezi vektorem polarizace a intenzitou pole. Uvedená anomálie byla poprvé zjištěna u tzv. Seignettovy soli (vínan sodnodraselný NaKC4H4O6.4H2O); později byla nalezena u řady dalších typů látek, jejichž klasickým představitelem je titaničitan barnatý BaTiO3.
Feroelektrické chování se vyskytuje pouze v určitém teplotním oboru, který je pro danou látku charakteristický, teplota TC omezující uvedený obor se nazývá feroelektrickou Curieovou teplotou. Charakteristická závislost vektoru polarizace na intenzitě pole je pro feroelektrické látky dána tzv. feroelektrickou hysterezní smyčkou (viz obr. 7.10). Polarizace vzorku feroelektrické látky, který byl ve výchozím stavu makroskopicky nezpolarizován, roste se vzrůstajícím polem nejdříve podle křivky 0Pm. Vzrůst je dosti rychlý, pokud polarizace nedosáhne určité nasycené hodnoty Ps. Při následujícím snižování pole klesá polarizace podle jiné křivky PmPs, takže nulovému poli odpovídá od nuly různá remanentní polarizace Pr. Dalšího snižování polarizace může být dosaženo přilo-žením pole opačného směru. Hodnota intenzity pole, při níž klesne polarizace opět na nulu, se nazývá feroelektrickým koercitivním polem. Při dalším zvyšování pole nabývá polarizace opačného směru a vzrůstá podle křivky -Ec- Pm do své nasycené hodnoty a při opětném snižování pole se proces opakuje podle křivky -PmPm. Opětné cyklické změny intenzity pole vyvolávají cyklické změny polarizace určené jednotlivými větvemi smyčky, která je určena body Pm,-Ec,-Pm,Ec,Pm. Žádné cyklické změny elektrického pole v daných mezích nemohou již převést vzorek do původního stavu, kdy nulovému poli odpovídala nulová hodnota polarizace. Pro titaničitan barnatý je při pokojové teplotě koercitivní pole v řádu 105 V.m-1, spontánní polarizace Ps ~ 0,26 C.m-2.
Průběh elektrické polarizace fereoelektrik při cyklickém polarizování je podobný chování feromagnetik (srov. článek 3.5.4). Feroelektrický stav je charakterizován tím, že jednotlivé elementární buňky krystalu mají nenulový elektrický dipólový moment. V nulovém nebo malém elektrickém poli jsou tyto dipólové momenty orientovány v určitých, krystalograficky význačných směrech. Celý objem krystalu se rozpadá na určitý počet oblastí, které se nazývají feroelektrické domény, z nichž každá je charakterizovaná určitou orientací výsledného dipólového momentu. Výsledný elektrický moment vzorku je pak dán vektorovým součtem momentů jednotlivých domén. Vnější elektrické pole relativně malých hodnot může značně ovlivnit rozdělení domén a vyvolat tak značně velkou výslednou polarizaci. Podobně jako u feromagnetik (srov. vztah (3.145) ) je možné zavést pojem efektivní permitivity jako poměr příslušných velikostí polarizace a intenzity pole. Takto zavedená veličina, která se obvykle uvažuje jen pro křivku prvotního polarizování, je ovšem obecně závislá na intenzitě elektrického pole. Může nabývat značně velikých hodnot (103 i více).
Jak plyne z tvaru hysterezní smyčky, může mít feroelektrický krystal nenulovou makroskopickou polarizaci i bez přítomnosti vnějšího elektrického pole. Může tedy principiálně sloužit jako zdroj elektrostatického pole. Ve skutečnosti je však tento způsob využití komplikován tím, že vázané náboje, které vznikají na povrchu krystalu v důsledku jeho polarizace, jsou postupně neutralizovány jednak konečnou vodivostí krystalu, jednak absorbováním nábojů přítomných v obklopující atmosféře.
Nad feroelektrickou Curieovou teplotou přechází feroelektrická látka do tzv. paraelektrického stavu, který je charakterizován silným poklesem permitivity při při zvyšování teploty. Chování permitivity v paraelektrickém stavu je zpravidla možné velmi dobře popsat vztahem
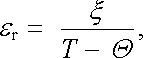 |
(7.13) |
v němž &ksi; je tzv. feroelektrická Curieova konstanta charakteristická pro daný materiál a Θ parametr blízký Curieově teplotě TC. Vztah (7.13) je feroelektrickou analogií Curieova-Weissova zákona pro paramagnetickou susceptibilitu feromagnetik (viz čl. 7.2.3).
Kromě feroelektrik existuje ještě jiný typ látek, které mohou mít trvalý elektrický moment. Látky tohoto druhu se nazývají elektrety. Jsou obvykle tvořeny směsí organických pryskyřic, popř. vosků, s dalšími organickými nebo anorganickými dielektriky. "Trvalý" elektrický moment lze například získat při tuhnutí této směsi v silném elektrickém poli, neboť vlastní elektrické momenty některých molekul (popřípadě makroskopických částic) zůstanou po zatuhnutí orientovány ve směru pole. Takto získaný nerovnovážný stav pak může být v látce zachován po velmi dlouhou dobu.
Každý feroelektrický krystal vykazuje rovněž tzv. piezoelektrický jev spočívající v tom, že elastickou deformací se mění elektrická polarizace krystalu. Feroelektrické krystaly vykazují i tzv. elektrostrikci, což je jev inverzní k jevu piezoelektrickému: při změně elektrického pole, které má za následek změnu elektrické polarizace, dochází ke vzniku elektrostrikční deformace. Piezoelektrické chování však mohou jevit i krystaly, které nejsou feroelektrické. Klasickým představitelem takových látek je krystalický křemen, na němž byl piezoelektrický jev P. Curiem v r. 1880 objeven.
Piezoelektrický jev je příkladem situace, kdy je elektrická polarizace vyvolána působením "neelektrických" sil. Fenomenologicky lze tento jev popsat lineárním vztahem mezi deformující silou a vzniklou elektrickou polarizací. Příslušná konstanta úměrnosti se nazývá piezoelektrickou konstantou. V současné elektronice má piezoelektrický jev významné uplatnění. Jednak je možné na jeho základě konstruovat elektromechanické měniče pro měřicí a regulační techniku, zejména však piezoelektrické mechanické rezonátory slouží jako stabilizační prvky frekvence elektronických oscilátorů.
Dielektrické vlastnosti látek lze vyložit na základě popisu mechanismů umožňujících vznik elektrických momentů atomů, molekul či elementárních buněk krystalů působením vnějšího elektrického pole, popř. jiných sil. Tyto procesy se popisují veličinou nazývanou polarizovatelnost a mohou mít různou fyzikální povahu. Existující tři základní typy takových mechanismů: elektronová polarizovatelnost, iontová polarizovatelnost a orientační dipolární polarizovatelnost. Elektronová polarizovatelnost zahrnuje deformaci elektronového obalu atomu v elektrickém poli, která má za následek posunutí těžiště elektronového náboje a vznik indukovaného elektrického momentu každého atomu. Iontovou polarizovatelností se rozumí vzájemné posunutí jednotlivých iontů například v molekule, čímž rovněž vzniká změna jejího dipólového momentu. Oba uvedené mechanismy nastávají ve všech typech látek, tedy i v látkách nepolárních. Konečně orientační polarizovatelností rozumíme změnu prostorové orientace vlastních momentů (například polárních molekul) účinkem vnějšího pole.
Podíl jednotlivých mechanismů na celkové permitivitě dané látky lze často rozlišit na základě studia její teplotní a frekvenční závislosti. V oddílu 7.6 uvidíme, že elektronová a iontová polarizovatelnost dává v zásadě teplotně nezávislý příspěvek, zatímco orientační polarizovatelnost příspěvek nepřímo úměrný teplotě. Orientační polarizovatelnost tvoří ve většině případů rovněž hlavní příspěvek ke statické permitivitě polárních látek. Jelikož však je tento mechanismus zpravidla spojen s pohybem značně hmotných útvarů (například molekul), přestává být efektivní při vyšších frekvencích. Polární látky se tudíž obvykle vyznačují značně rozdílnými hodnotami mezi statickou a vysokofrekvenční permitivitou. Pohyblivost polárních molekul se může značně zvýšit při přechodu látky z pevného do kapalného skupenství. Tímto způsobem lze kvalitativně pochopit větší hodnoty permitivity polárních látek v kapalném skupenství.
Další zajímavou vlastnost dielektrických vlastností látek představuje existence ferolelektrického jevu. Přesto, že makroskopické projevy feroelektrik jsou do značné míry podobné chování feromagnetik, je fyzikální podstata obou jevů zásadně odlišná, neboť vlastní elektrické momenty nemohou (na rozdíl od momentů magnetických) vznikat na atomové úrovni. Vznik feroelektrického spontánního uspořádání se týká vlastních elektrických momentů elementárních buněk krystalu, a je tudíž mnohem více než feromagnetismus vázáno na konkrétní vlastnosti krystalové struktury. Feroelektrický jev může vzniknout jen u krystalových struktur, které nemají střed symetrie. Ke kvantitativnímu výkladu jeho vlastností je možné použít jednak zákonů termodynamiky (srov. čl. 5.2.3) a jednak modelové mikroskopické teorie[53] .
Základní údaje o magnetických vlastnostech látek byly vyloženy již v článku 3.5.4. Jak bylo uvedeno, pro diamagnetika i paramagnetika jsou (s výjimkou extrémně vysokých polí a extrémně nízkých teplot) charakteristické lineární materiálové vztahy, přičemž diamagnetika se vyznačují zápornou magnetickou susceptibilitou χ m (a tedy relativní permeabilitou μ r < 1), zatímco paramagnetika mají kladnou magnetickou susceptibilitu (a relativní permeabilitu μ r > 1). Hodnoty relativní permeability obou typů látek se přitom jen málo liší od jedné[54] .
V tabulce 7.4 jsou uvedeny příklady hodnot magnetické susceptibility některých látek při pokojové teplotě, obr. 7.11 ukazuje reprezentativní příklady její teplotní závislostí. Jak je vidět z obrázku, je susceptibilita diamagnetik velmi málo teplotně závislá, podobně susceptibilita některých paramagnetických kovů je v podstatě teplotně nezávislá. Naproti tomu jiné kovy (například Pd, Pt aj.) a též téměř všechna nekovová paramagnetika jeví výraznou teplotní závislost susceptibility.
Obrázek 7.12 zobrazující teplotní závislost měrné susceptibility κ m pro CuK2(SO4)2.6H2O, demonstruje platnost Curieova zákona (3.144)
Tabulka 7.4 Hodnoty magnetické susceptibility některých diamagnetik a paramagnetik
|
diamagnetika |
paramagnetika |
||
|
látka |
mag.susceptibilita při teplotě T = 293 K |
látka |
mag.susceptibilita při teplotě T = 293 K |
|
antimon bismut stříbro zlato zinek měď křemík voda etylalkohol |
- 6,8 .10-5 - 16,0 .10-5 - 2,51 .10-5 - 3,4 .10-5 - 1,56 .10-5 - 0,97 .10-5 - 0,32 .10-5 - 0,905.10-5 - 0,73 .10-5 |
sodík draslík hliník palladium platina yttrium chlorid nikelnatý |
+ 8,5 .10-4 + 5,7 .10-4 + 0,2 .10-4 + 8,2 .10-4 + 2,9 .10-4 + 1,18.10-4 + 1,1 .10-4 |
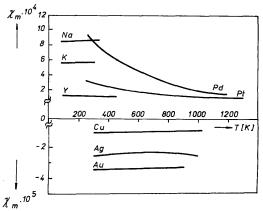
Obr. 7.11 Příklady
teplotní závislosti magnetické susceptibility
paramagnetických a diamagentických kovů

Obr. 7.12 Příklad teplotní závislosti magnetické susceptibility
nekovového paramagnetika splňující Curieův zákon.
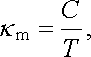 |
který je charakteristický pro nekovová paramagnetika.
Diamagnetismus je obecný jev, jehož podstata spočívá ve změnách elektronových stavů vyvolaných vnějším magnetickým polem, které mohou být intuitivně chápány jako důsledek zákona elektromagnetické indukce, podle něhož změny vnějšího magnetického pole indukují v látce proudy vytvářející vlastní magnetické pole působící proti těmto změnám. Při vložení do vnějšího magnetického pole tedy v celém objemu látky vznikají dodatečné magnetické momenty, které se snaží vnější magnetické pole kompenzovat. Vzhledem k tomu, že jev elektromagnetické indukce platí zcela obecně, je i diamagnetický jev obecnou vlastností všech látek. V některých případech však může být překryt projevy vlastních magnetických momentů některých elektronů, které jsou zdrojem paramagnetismu.
Diamagnetické látky jsou zpravidla nejméně magneticky aktivní. Jejich magnetická susceptibilita je v absolutní hodnotě obvykle mnohem menší než susceptibilita jiného typu látek. Tato malá magnetická aktivita diamagnetik vedla k domněnce, že atomy, respektive molekuly těchto látek mají v nulovém magnetickém poli nulový magnetický moment, což znamená, že neobsahují částečně zaplněné podslupky. Teprve vnější magnetické pole indukuje dodatečné magnetické momenty vytvářející makroskopickou magnetizaci diamagnetika.
V článku 7.6.2 bude uvedena stručná verze Langevinovy teorie diamagnetismu volných molekul, která představuje historicky první kvantitativní teorii tohoto jevu. Teorie je založena na výpočtu dodatečného indukovaného magnetického momentu vznikajícího Larmorovou precesí elektronových magnetických momentů (srov. článek 6.2.2) a podává v podstatě správný obraz o diamagnetismu nekovových látek.
V případě kovů je vedle diamagnetického chování lokalizovaných vnitřních elektronů v atomech třeba počítat ještě s vlivem vodivostních elektronů, jejichž diamagnetismus nelze popsat vztahy plynoucími z Langevinovy teorie. Teorii diamagnetismu volných elektronů vypracoval L. D. Landau. I když jde o teorii kvantově mechanickou, možnost vzniku diamagnetického příspěvku k susceptibilitě volných elektronů lze pochopit i názorně, uvědomíme-li si charakter jejich pohybu v magnetickém poli (viz článek 6.1.3).
Paramagnetické vlastnosti jsou na rozdíl od diamagnetismu dány nevykompenzovanými magnetickými momenty některých elektronů v atomu. Paramagnetické chování tedy jeví látky obsahující atomy či molekuly s částečně zaplněnými elektronovými podslupkami. Paramagnetismus lokalizovaných magnetických momentů řeší Langevinova teorie paramagnetismu, která bude popsána v článku 7.6.3 a která (po zavedení kvantově mechanických korekcí) správně popisuje paramagnetismus nekovových látek. Zejména z této teorie vyplývá platnost Curieova zákona (3.144) .
Specifickým problémem je paramagnetismus kovů, na němž se výrazně podílí vodivostní elektrony. Jak jsme viděli v obr. 7.11, charakteristickým rysem magnetismu některých kovů přitom je teplotní nezávislost jejich susceptibility. Je zřejmé, že teplotně nezávislý paramagnetismus vodivostních elektronů nemůže být vyložen na základě klasického modelu elektronového plynu. Každý elektron má totiž spinový magnetický moment velikosti μ B, který může být vnějším magnetickým polem orientován do jiného směru. Při aplikaci klasické statistiky bychom dostali situaci analogickou jako v Langevinově teorii a pro teplotní závislost susceptibility by vyšel vztah typu (3.144) , kde C = μ 0n0m2/3kB (srov. vztah (7.68) ).
Problém paramagnetismu elektronového plynu vyřešil W. Pauli, který vzal v úvahu vlastnosti Fermiho-Diracova rozdělení (viz článek 7.1.3). Podstatu problému je možné snadno pochopit i kvalitativně. Vnější magnetické pole sice energeticky zvýhodňuje určitou (paralelní) orientaci magnetických momentů elektronů, většina elektronů však nemůže tuto výhodnější orientaci zaujmout, neboť pro energie podstatně nižší, než je Fermiho energie, jsou již všechny tyto stavy obsazeny (srov. obr. 7.6). Na vnější magnetická pole mohou reagovat jen elektrony, jejichž energie je blízká Fermiho energii, přičemž je zřejmé, že se vzrůstající teplotou počet takových elektronů vzrůstá. Lze ukázat, že relativní počet těchto elektronů je roven T/TF, kde TF = EF/kB (viz čl. 7.1.3). Potom pro odhad paramagnetické susceptibility elektronového plynu dostaneme teplotně nezávislý výraz
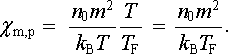 |
(7.14) |
Přesný výpočet dává hodnotu
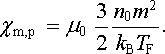 |
(7.15) |
která se nazývá Pauliho paramagnetickou susceptibilitou elektronového plynu.
Jak bylo již výše řečeno, elektronový plyn však jeví i diamagnetismus Landauova typu, jehož diamagnetická susceptibilita χ m,L se musí připočíst k susceptibilitě Pauliho. Výpočet dává χ m,L = - χ m,P/3 Výsledná suceptibilita elektronového plynu je tedy rovna
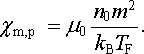 |
(7.16) |
Na základě právě vyložených skutečností je možné podat hrubý a do značné míry zjednodušený obraz o magnetických vlastnostech kovů, který však správně vystihuje jejich fyzikální podstatu. Výsledná magnetická susceptibilita je dána součtem příspěvků jednotlivých typů elektronů. U všech kovů se vyskytuje paramagnetismus vodivostních elektronů daný vztahem (7.16) a diamagnetismus lokalizovaných elektronů vnitřních zaplněných slupek, který je popsán Langevinovou teorií (viz čl. 7.6.2). Magnetická susceptibilita kovů, které neobsahují částečně zaplněné vnitřní podslupky, je v zásadě dána bilancí těchto teplotně nezávislých příspěvků. U lehkých kovů (například u sodíku) převažuje magnetismus vodivostních elektronů, takže jsou paramagnetické. U těžších kovů (například měď), u nichž je větší počet lokalizovaných elektronů ve vnitřních slupkách, může naopak převážit jejich diamagnetismus. U kovů, u nichž mohou být nezaplněné stavy ve vnitřních podslupkách, se může navíc projevit paramagnetismus těchto nezaplněných podslupek. Vzhledem k tomu, že elektrony takových podslupek mohou být do značné míry lokalizované, může jít o teplotně závislý paramagnetismus Langevineova typu (viz článek 7.6.3). Příkladem takového chování je palladium a platina.
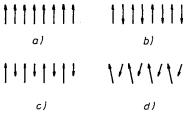
Již v článku 3.5.4 bylo vyloženo, že fyzikální podstatou silného magnetismu je spontánní uspořádání magnetických momentů atomů, přičemž silný magnetismus jeví látky s takovým typem uspořádání, u něhož nejsou atomové momenty vzájemně vykompenzovány. Existuje několik klasických typů struktur magnetického uspořádání, které jsou uvedeny na obr. 7.13. Obrázek 7.13a představuje feromagnetickou strukturu, u níž jsou všechny atomové magnetické momenty stejné velikosti uspořádány paralelně. Obrázek 7.13b ukazuje tzv. antiferomagnetickou strukturu, v níž se střídají antiparalelně orientované magnetické momenty stejné velikosti, které se vzájemně kompenzují, takže výsledný magnetický moment struktury je nulový. Soustava stejně orientovaných magnetických momentů se nazývá magnetickou podmřížkou. Antiferomagnetickou strukturu můžeme tedy popsat jako průnik dvou magnetických podmřížek s opačně orientovanými momenty stejné velikosti. Obrázek 7.13c dále zobrazuje schéma ferimagnetické struktury, která je reprezentována rovněž dvěma antiparalelně orientovanými magnetickými podmřížkami, každá z nich však obsahuje momenty jiné velikosti, takže výsledný moment není vykompenzován. Konečně obr. 7.13d uvádí příklad obecnějšího uspořádání, v němž všechny magnetické momenty nemají stejný směr. Jde o příklad tzv. nekolineární struktury, jejíchž konkrétních typů je v současné době známa celá řada. Jelikož však jde vesměs o materiály exkluzivních vlastností, nebudeme se strukturami tohoto typu dále zabývat.[55]

Magnetické uspořádání existuje vždy při teplotách nižších, než je jistá kritická teplota. V případě feromagnetik mluvíme o Curieově teplotě TC, v případě ferimagnetik a antiferomagnetik o teplotě Néelově TN. Nad Curieovou, popř. Néelovou, teplotou jsou tyto látky paramagnetické a jejich magnetická susceptibilita s rostoucí teplotou klesá. S výjimkou bezprostředního okolí kritické teploty často splňují tzv. Curieův-Weissův zákon
(eq0028) (7.17)
který je modifikací Curieova zákona (3.144) (srov. rovněž analogické chování feroelektrik - viz článek 7.2.1). Konstanta CW je analogií Curieovy konstanty v (3.144) . Veličina Θ má rozměr teploty. V případě feromagnetik se obvykle příliš neliší od Curieovy teploty,[56] v případě antiferomagnetik je však značně odlišná od Néelovy teploty a je dokonce záporná.
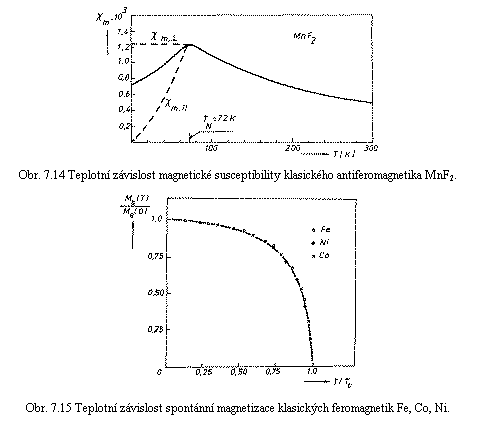
Vzhledem k tomu, že v
antiferomagnetické struktuře jsou magnetické momenty jednotlivých podmřížek
vzájemně vykompenzovány, jeví se antiferomagnetika jako slabě magnetické
látky. Jako příklad uvádíme na obr. 7.14 teplotní průběh magnetické
susceptibility klasického antiferomagnetika MnF2 s Néelovou
teplotou T
N
= 72 K. Nejvyšší hodnotu má
susceptibilita v okolí Néelovy teploty, je však stejného řádu jako
susceptibilita silnějších paramagnetik. Nad Néelovou teplotou susceptibilita s
rostoucí teplotou klesá, splňuje Curieův-Weissův zákon
(7.17)
s hodnotou = -113 K. Pod Néelovou teplotou jsou
vlastnosti antiferomagnetik obvykle anizotropní. Plná křivka na obrázku reprezentuje
průběh susceptibility polykrystalického vzorku, čárkované křivky popisují
chování susceptibility monokrystalu: χ
m,||
v případě, že magnetické pole je rovnoběžné se směrem momentů magnetických
podmřížek, χ
m,⊥
v případě magnetického pole orientovaného kolmo.
Společným rysem feromagnetického a ferimagnetického uspořádání je existence nenulového výsledného magnetického momentu. Touto skutečností je podmíněno podobné chování obou typů látek ve vnějším magnetickém poli, které může být popsáno hysterezní smyčkou, popř. jejími jednotlivými parametry, jako spontánní a remanetní magnetizací, koercitivním polem, počáteční a maximální permeabilitou a jinými (viz článek 3.5.4).
Spontánní magnetizace Ms je základní parametr feromagnetika (popř. ferimagnetika), který popisuje stav jeho magnetického uspořádání. Charakteristickým způsobem, který pro klasická ferimagnetika ukazuje obr. 7.15, se mění Ms s teplotou. Pro ferimagnetika má teplotní průběh spontánní magnetizace obvykle kvalitativně stejný charakter.

Obr. 7.16 Základní mechanismy magnetování feromagnetik: a) doménová struktura v nulovém magnetickém poli, b) magnetování posuvem doménových stěn, c) magnetování stáčením magnetizace v doménách.
Konkrétní souvislost mezi hodnotou makroskopické magnetizace vzorku a hodnotou přiloženého magnetického pole je podmíněna tím, že při teplotách nižších než TC (popř. TN) se celý objem látky rozpadá na určitý počet oblastí, tzv. magnetických domén, které jsou spontánně zpolarizovány. Vektor výsledné magnetizace každé z nich má tendenci být orientován do význačných krystalografických směrů, tzv. snadných směrů magnetizace. Výsledný magnetický moment vzorku je pak dán vektorovým součtem momentů jednotlivých domén; vnější magnetické pole relativně malých hodnot může tedy vyvolat značné změny výsledné magnetizace. Obrázek 7.16 schematicky ukazuje způsob magnetování klasických kovových feromagnetik. V nulovém magnetickém poli mají domény konfiguraci tvořící uzavřené "magnetické obvody", která je energeticky výhodná. Se vzrůstem pole H se nejdříve zvětšuje objem domén se směrem magnetizace blízkým směru vnějšího pole, dále se magnetizace v jednotlivých doménách vytáčí do směru vnějšího pole až nakonec (při dostatečně vysokém poli) je celý objem vzorku zmagnetován ve směru pole.
V článku 3.5.4 byly naznačeny způsoby technického využití silně magnetických materiálů. Pro magneticky měkká i magneticky tvrdá magnetika se používají jak kovové materiály vycházející z klasických feromagnetik a jejich slitin, tak ferimagnetika, z nichž největší technický význam mají tzv. ferity, což jsou oxidy železa a jiných kovů. V tabulkách 7.5 a 7.6 uvádíme pro informaci několik údajů o nejběžnějších magneticky měkkých a magneticky tvrdých materiálech.
Tabulka 7.5. Příklady permability magneticky měkkých magnetik
|
látka |
počáteční perm. μ r,p poč. perm. |
maximální perm.μ r,max |
Hc (A/m) |
Pm,r (Wb/m2) |
|
transformátorová ocel (96%Fe,4%Si) čisté železo (99,95% Fe) 78-permalloy (21,2%Fe,78,5%Ni,,3%Mn) supermalloy (15,7%Fe,79%Ni,5%Mo,0,3%Mn) manganatozinečnatý ferit (Mn0,5Zn0,5Fe2O4) |
4 .102 1 .104 6 .103
1 .105
až 5 .103 |
6,7 .103 1,8 .105 1 .105
1 .106
|
40 4 4
0,32
10 |
1,2 2,15 1,07
0,8
0,4 |
Tabulka 7.6 Příklady parametrů magneticky tvrdých materiálů
|
látka |
Hc (A/m) |
Pm,r (Wb/m2) |
|
uhlíková ocel (98,1% Fe, 1% Mn, 0,9% C) |
4 .103 |
1,0 |
|
kobaltová ocel (52,6% Fe, 36% Co, 7% W, 3,5% Cr, 0,9% C) |
18,3.103 |
1,0 |
|
Alnico V (51% Fe, 14% Ni, 8% Al, 24% Co, 3% Cu) |
52 .103 |
1,27 |
|
barnatý ferit: -izotropní |
135 .103 |
0,21 |
|
-anizotropní |
135 .103 |
0,21 |
Fyzikální příčinou vzniku magnetického uspořádání je tzv. výměnná interakce mezi elektrony částečně zaplněných podslupek (viz čl 7.1.4), která je elektrické povahy, může však být popsána jen na základě zákonitostí kvantové mechaniky. Podrobnější výklad podstaty magnetického uspořádání přesahuje možnosti této knihy. Fenomenologicky může být vznik magnetického uspořádání vyložen na základě předpokladu o existenci tzv. molekulárního pole, které v r. 1907 zavedl P. E. Weiss. Existence magnetického uspořádání vyplývá za tohoto předpokladu z Langevinovy teorie paramagnetismu. Později byl podobný postup použit i L. Néelem pro výklad vlastností ferimagnetik.
V současné době tvoří fyzika magneticky uspořádaných materiálů rozsáhlou oblast fyziky pevných látek, která má k dispozici celou řadu experimentálních metod umožňujících přímé studium jak magnetického uspořádání, tak magnetizačních procesů a doménové struktury. Na základě poznání fyzikální podstaty magnetického uspořádání je možné připravovat stále dokonalejší materiály pro technické aplikace. V poslední době mají největší význam materiály pro záznam informace, magneticky měkké materiály na bázi kovových skel, magneticky tvrdé materiály na bázi vzácných zemin a jiné.