---

---

7.1 *Elektronová struktura látek

7.1.1 Energie elektronů v atomech a molekulách

Nejdůležitější intereakcí určující energii elektronu ve volném atomu je, jak víme, elektrická interakce mezi tímto elektronem a jádrem. Elektrickou interakcí (srov. kapitolu l) je ovšem energie určena až na libovolnou konstantu, kterou je třeba zvolit. Obvykle se za nulovou považuje energie elektronu s nulovou rych­lostí, který je nekonečně vzdálen od jádra. Potom elektrony s celkovou kladnou energií můžeme považovat za volné a naopak elektrony s energií zápornou za vázané v atomech. Z kvantové mechaniky vyplývá (viz např. [l]), že volné elektrony mohou mít spojité spektrum energie, zatímco elektrony vázané v atomu se mohou nacházet jen ve stavech s určitými diskrétními hodnotami energie, které tvoří diskrétní spektrum.

V nejjednodušším atomu s jedním elektronem, tj. v atomu vodíku, je (v přiblížení nerelativistické kvantové mechaniky) energie elektronu W_n určena jen tzv. hlavním kvantovým číslem n, které může nabývat hodnot přirozených čísel n = 1, 2, 3, ... Platí

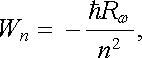(7.1)

kde R_ω  = (₀c²/4π )²(m_ee⁴/2h³) B 2,067.10^-16s^-1 je tzv. Rydbergova úhlová frek­vence, h = h/2π a h = 6,626 176.10^-34 J.s je Planckova konstanta[47] . Na obrázku 7.1 vidíme zjednodušené schéma energetických hladin elektronu v atomu vodíku odpovídajících vztahu (7.1) . Stavy odpovídající těmto energiím se nazývají sta­cionární stavy a elektrony v těchto stavech nevyzařují energii. Naopak při pře­chodu mezi různými stacionárními stavy musí elektron odevzdat či získat urči­tou energii, obvykle ve formě kvanta elektromagnetického záření - fotonu. Jak je z obrázku vidět, nejnižší energii má elektron ve stavu n = l, který se nazývá základní stav. Elektron v tomto stavu musí získat energii alespoň W_i = hR_ω  = 13,6 eV, aby se z atomu uvolnil. Tato energie se nazývá ionizační energie. Příslušný rozdíl potenciálu, kterým musí elektron projít, aby získal tuto energii, se nazývá ionizační potenciál.

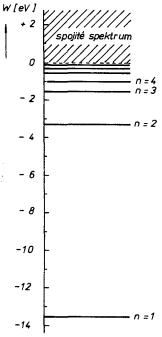
Vedle energie má elektron v atomu ještě určité diskrétní hodnoty momentu hybnosti svázané s jeho pohybem kolem atomového jádra. Ve stavu s danou hodnotou hlavního kvantového čísla n je velikost tohoto tzv. orbitálního mo­mentu L, určena "vedlejším" kvantovým číslem l, které může nabývat hodnot l = 0, 1, 2, ...,(n - 1). Platí

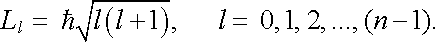(7.2)

Orbitální moment v daném stacionárním stavu má určitou jen jedinou složku do daného, předem zvoleného směru, určeného například směrem vnějšího pole, do kterého položíme osu z soustavy souřadné. Při dané hodnotě kvantového čísla l je velikost této složky určena tzv. magnetickým kvantovým číslem m_l , které může nabývat 2l + l hodnot m_l  = l, (l - 1), (l - 2),...,-l. Platí

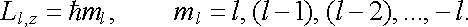(7.3)

Můžeme tedy uzavřít: Orbitální stav elektronu v atomu vodíku je určen třemi kvantovými čísly: n, l, m_l . Hlavní kvantové číslo n určuje energii stacionárního stavu podle vztahu (7.1) , vedlejší kvantové číslo l určuje velikost orbitálního momentu hybnosti podle vztahu (7.2) a magnetické kvantové číslo m_l určuje "orientaci" tohoto momentu vůči danému směru podle vztahu (7.3) .

Elektron má však ještě vlastní moment hybnosti nazývaný spin.[48] Jeho vlast­nosti jsou (podobně jako vlastnosti orbitálního momentu) podřízeny obecným kvantově mechanickým pravidlům pro moment hybnosti. To znamená, že veli­kost spinu a jeho možné složky jsou popsány dvěma kvantovými čísly: spino­vým kvantovým číslem s a magnetickým kvantovým číslem m_s . Z experimentu i z relativistické kvantové mechaniky vyplývá s = 1/2. V analogii s (7.2) a (7.3) pak pro velikost spinu L_s a pro jeho složku L_s,z do daného význačného směru platí

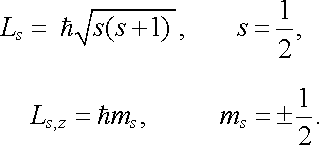(7.4)

Protože kvantové číslo s = 1/2 je pro elektron jednoznačně dáno, může se při změně stavu elektronu měnit jen "prostorová orientace" spinu, která je určena magnetickým spinovým kvantovým číslem m_s . Toto kvantové číslo tvoří, vedle zmíněných kvantových čísel n, l, m_l , čtvrtý parametr charakterizující stav elek­tronu vázaného v atomu vodíku.

V případě atomů s více elektrony zůstává situace kvalitativně stejná. Stavy jednotlivých elektronů vázaných v atomu jsou popsány čtveřicí uvedených kvantových čísel, přičemž energie elektronů v těchto stavech může nabývat opět jen určité diskrétní hodnoty. Podstatný rozdíl je však v tom, že při určování elektronových stavů je vedle elektrické interakce elektronu s jádrem třeba uva­žovat ještě další vzájemné interakce mezi elektrony. Nejdůležitější je elektrická (coulombovská) interakce mezi elektrony, která vede především k tomu, že energie daného stacionárního stavu závisí nejen na hlavním kvantovém čísle n, ale také na vedlejším kvantovém čísle l.

Z právě uvedených faktů vychází obvyklé značení elektronových stavů v atomu, které rozlišuje jen stavy s různou energií, a využívá tudíž kvantových čísel n a l. Soubor elektronových stavů s danou hodnotou hlavního kvantového čísla se nazývá slupkou elektronového obalu uvažovaného atomu. Podle histo­ricky zavedené symboliky jsou jednotlivé slupky, které odpovídají hodnotám n = l, 2, 3, 4, ... postupně označovány písmeny K, L, M, N, .... V dané slupce může existovat několik skupin elektronových stavů lišících se kvantovým číslem l (a tedy i energií). Tyto skupiny stavů se nazývají podslupky a pro hodnoty l = 0, 1, 2, 3, 4, ... se pro označení podslupky používají postupně symboly s, p, d, f, ... Například tedy ve slupce M existují podslupky 3s, 3p, 3d.

Pro elektronovou strukturu atomu s více elektrony má principiální význam způ­sob obsazování možných stavů, který musí vyhovovat tzv. Pauliho principu. Tento princip je důsledkem nerozlišitelnosti částic v kvantové mechanice a pro případ elektronů v atomu říká, že v daném stavu popsaném kvantovými čísly n, l, m_l , m_s se může nalézat nejvýše jeden elektron. V základním stavu, tj. ve stavu, ve kterém může setrvávat libovolně dlouho, má atom nejnižší možnou energii, a jsou tedy v souladu s Pauliho principem obsazeny stavy s nejnižší energií. Na obrázku 7.2 je uveden příklad elektronové struktury neutrálního atomu Na, který obsahuje 11 elektronů. Atom má plně obsazeny slupky K a L obsahující po­stupně 2 a 8 elektronů. Ve slupce M, která má 18 elektronových stavů, je jen jediný elektron ve stavu 3s.

Pro chemické a elektrické vlastnosti atomu je důležitá prostorová symetrie rozložení náboje v elektronovém obalu a zejména její odchylky od symetrie kulové. Z tohoto hlediska mají zvláštní postavení stavy typu "s", jimž samotným odpovídá kulově symetrické rozložení náboje. Rovněž zcela zaplněné podslupky mají tuto vlastnost; zdrojem odchylek od kulově symetrického rozložení náboje jsou tedy částečně zaplněné podslupky typu p, d, f, ...

Na stupni zaplnění periferní podslupky jsou rovněž silně závislé schopnosti atomu tvořit ionty. Tuto skutečnost jasně dokumentuje obr. 7.3[49] , ve kterém je vynesena závislost ionizační energie W_i, potřebné pro vznik kladných iontů, na atomovém čísle Z. Je vidět, že tato závislost sleduje periodicitu Mendělejevovy tabulky, která je dána stupněm zaplněnosti periferní podslupky. Nejsnáze tvoří kladné ionty alkalické kovy, zatímco nejvyšší ionizační energii mají inertní plyny. Z obrázku je rovněž vidět, že nesnadno tvoří kladné ionty i atomy s téměř zaplněnou periferní podslupkou, především atomy halogenových prvků. Tyto atomy mají naopak schopnost udržet nadbytečné elektrony a tvořit ionty záporné.

Obr. 7.3 Ionizační energie neutrálních atomů.

Uvedenou vlastnost lze kvalitativně vyložit jednoduchou úvahou: V elektri-cky neutrálním atomu je kladný náboj jádra vykompenzován záporným nábojem elektronů. Elektrické pole jednotlivých nabitých částic v atomu je však plně vykompenzováno a atom se chová jako elektricky neutrální útvar jen v dosta-tečně velké vzdálenosti, přičemž stupeň kompenzace závisí na symetrii rozložení náboje elektronů (srov. vlastnosti multipólového rozvoje elektrického pole - čl. 1.3.1). V prostoru samotné periferní podslupky zůstává část kladného náboje jádra lokálně nevykompenzována, čímž vzniká možnost lokalizace nad­bytečného elektronu. Vzniklý záporný iont může být energeticky výhodnější než příslušný neutrální atom. Tato vlastnost se nazývá afinita atomu k elektronu a příklady hodnot W_a (tj. rozdílu energie neutrálního atomu v základním stavu a energie záporného iontu) pro některé prvky jsou uvedeny v tabulce 7.1

Z uvedeného příkladu je patrné, že existence volného atomu s nezaplněnou podslupkou nemusí být energeticky výhodná, přičemž afinita daného atomu k elektronu se může projevit i vytvořením molekuly. V principu existují dvě mezní situace v charakteru vazby atomů v molekule: vazba heteropolární (ion­tová) a vazba homopolární. Molekuly s heteropolární vazbou vznikají z atomů různého druhu, z nichž jeden má tendenci tvořit kladné ionty a druhý ionty zá­porné. Molekulu si pak můžeme představit jako soustavu kladných a záporných iontů, které jsou přitahovány elektrickou silou; příkladem může sloužit molekula NaCl. Naopak homopolární molekuly vznikají z atomů stejného či podobného typu. Typickými příklady jsou molekuly H₂, N₂, O₂ a jiné. Charakteristickým rysem homopolární vazby jsou kolektivizované stavy elektronů podílejících se na vazbě. Fyzikální podstatu homopolární vazby však nelze vyložit na základě klasických představ. Důležitou roli při jejím vzniku má tzv. výměnná interakce mezi vazebními elektrony, která je čistě kvantově mechanickým důsledkem elektrické interakce a je odpovědná i za řadu vlastností kondenzovaných látek (například za magnetické uspořádání - viz článek 7.2.3).

Tabulka 7.1 Afinita některých atomů k elektronu

Podobně jako v případě atomů, odpovídají i jednotlivým stacionárním sta­vům molekuly diskrétní hodnoty energie. Situace je zde poněkud složitější, ne­boť stav molekuly jako celku je určen nejen vlastními stavy elektronu, ale také vzájemným pohybem atomů v molekule, popř. pohybem celé molekuly. Změna stavu elektronu je vždy doprovázena změnami kmitů atomů a změnami rotač­ního pohybu molekuly. Proto má energetické spektrum molekuly jako celek zmíněný diskrétní charakter. Avšak na rozdíl od energetického spektra atomu, které je zpravidla tvořeno soustavou vzájemné dosti vzdálených hladin, sestává energetické spektrum molekuly ze skupin blízkých hladin. Mluvíme o tzv. páso­vém spektru.

Tabulka 7.2 Disociační energie některých molekul

Molekuly mohou být (stejně jako atomy) ionizovány. Molekula může popsa­ným mechanismem zachytit jeden či více nadbytečných elektronů, čímž vznikne záporný iont. Naopak, ztratí-li molekula jeden či více elektronů, vznikne iont kladný. Například ionizační energie potřebná pro vznik iontu H₂⁺ činí 15,43 eV. Na druhé straně afinita molekuly H₂ k elektronu činí 0,72 eV.

Získají-li atomy energii, která převyšuje energii jejich vazby v molekule, může dojít k jejímu rozdělení. Mluvíme o disociaci molekuly a energii potřeb­nou k disociaci nazýváme disociační energií. Jako příklad uvádíme v tabulce 7.2 disociační energii W_D některých dvouatomových molekul.

7.1.2 Energie elektronů v kondenzovaných látkách

V předchozím článku jsme viděli, že pro objasnění chování elektronů v atomu a molekule jsou podstatné zákony kvantové mechaniky. Jejich důsledkem pře­devším bylo, že elektrony v atomech mohou existovat jen v určitých stavech s definovanými diskrétními hodnotami energie a orbitálního a spinového mo­mentu hybností, přičemž tyto možné stavy jsou obsazovány v souladu s Pauliho principem. Současně jsme viděli, že při přechodu od atomu k molekule se ener­getické spektrum značně zkomplikovalo vlivem podstatně větší variability po­hybového stavu molekuly. V tomto článku nás bude zajímat otázka, jaké energie mohou mít elektrony v kondenzovaných látkách. V principu je tuto otázku v plném rozsahu schopna řešit kvantová mechanika. Ve skutečnosti ovšem, pro­tože jde o problém velmi mnoha částic, je možné použít jen aproximativní metody různého přiblížení vypracované použitím zákonů kvantové mechaniky, které jsou aplikované pomocí počítačů. Na tomto místě můžeme uvést jen kva­litativně některé příklady výsledků takových výpočtů. Budeme sledovat myšlen­kový pokus vzniku kovového krystalu sodíku,[50] který nám umožní pochopit podstatu problému.

Jak víme, sodík má za pokojové teploty kubickou prostorově centrovanou strukturu s mřížkovou konstantou a = 0,43 nm. Vzdálenost nejbližších sousedů v krystalové mřížce činí R₀ = 0,37 nm, hustota ρ _M = 968 kg.m^-3. V krystalu o objemu l cm³ je tedy přibližně N = 3.10²² atomů. Předpokládejme nejdříve, že jednotlivé atomy jsou navzájem značně vzdáleny, například na vzdálenost R = l cm. Elektrony každého atomu se nacházejí ve stavech popsaných v pravé části obr. 7.4 (srov. obr. 7.2).

Sledujme nyní myšlenkový proces, při kterém se atomy postupně sbližují až na vzdálenost R₀ = 0,37 nm, takže vznikne krystal kovového sodíku. Je zřejmé, že elektrony sousedních atomů, a to především elektrony ve vnějších podslup­kách, se budou stále více ovlivňovat. Výpočet ukazuje, že každá z dovolených energetických hladin atomu se rozštěpí N-krát, takže vzniknou kvazispojité in­tervaly dovolených energií oddělených intervaly E_g energií zakázaných; v lite­ratuře se obvykle mluví o dovolených a zakázaných pásech (viz obr. 7.4). Šířka výše položených pásů dovolených energií bývá řádově jednotky až desítky eV. Například u sodíku je šířka pásu 3s rovna 6,24 eV. Naproti tomu pásy vzniklé z hladin vnitřních podslupek jsou zpravidla značně užší. Například pás 1  s so-díku má šířku jen asi 10^-19 eV.

Vezmeme-li v úvahu počty elektronových stavů v jednotlivých podslupkách atomu sodíku, snadno určíme počty stavů v jednotlivých dovolených pásech krystalu sodíku: pásy 1s, 2s, 3s mají 2N stavů, pás 2p má 6N stavů. V pásech 1s, 2s a 2p jsou všechny možné stavy zaplněny, zatímco pás 3s je zaplněn jen zpo­loviny. "Pod lupou" na obr. 7.4 vidíme strukturu dvou periferních pásů a charakter zaplňování jejich jednotlivých hladin. Předpokládáme-li šířku pásu 10 eV a počet hladin v pásu N ~ 10²², můžeme odhadnout průměrný rozdíl ener­gií nejbližších hladin v pásu Δ E ~  10^-21 eV.

Obr. 7.4 K výkladu vzniku pásové struktury energie elektronů v krystalu sodíku.

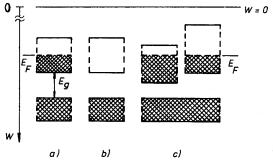
Způsob zaplnění pásů dovolených energií, který jsme viděli u sodíku, je charakteristický pro kovy, jež mají vnější (periferní) pás zaplněn vždy jen zčásti. Jiná situace nastává u krystalických látek, jejichž atomy mají periferní slupku zcela zaplněnou. Takové látky mají v základním stavu, tj. například při teplotě absolutní nuly, jednotlivé pásy dovolených energií buď zcela zaplněné, nebo zcela prázdné. U látek se složitější elektronovou strukturou může nastat překrytí dvou pásů odpovídajících různým atomovým podslupkám. V základním stavu jsou pak oba tyto pásy zaplňovány elektrony do stejných hodnot energie, která se nazývá Fermiho energií E_F (srov. čl. 7.1.3). Na obrázku 7.5 je uvedeno srovnání pásové struktury uvedených tří typů krystalických látek.

Detailnější výpočty elektronových stavů v pevných látkách ukazují, že elektrony tvořící úzké pásy zůstávají silně lokalizovány v jednotlivých atomech. Naopak elektrony tvořící široké pásy mají značnou pravděpodobnost "samovol­ného přeskoku" z jednoho atomu na druhý. O elektronech z nejširších perifer­ních pásů lze s dobrým přiblížením předpokládat, že se mohou v podstatě volně pohybovat v celém objemu krystalu. Tento pohyb je ovšem chaotický, může však mít značné rychlosti. Například střední rychlost chaotického pohybu elektronů v pásu šířky 10 eV činí řádově 10⁶ m.s^-1.

Právě popsaný charakter elektronové struktury krystalických pevných látek má principiální důležitost pro pochopení většiny jejich fyzikálních vlastností, mezi jiným i elektrické vodivosti. Podstata problému spočívá v tom, že elektrony ve zcela zaplněných pásech se na elektrické vodivosti nemohou podí­let, i když může jít o elektrony do značné míry nelokalizované. Elektrické pole nemůže totiž těmto elektronům udělit dodatečnou energii potřebnou pro uspořá­daný pohyb v makroskopickém měřítku, neboť v daném pásu nejsou již k dispo­zici potřebné volné stavy. Naproti tomu v částečně zaplněném pásu, ve kterém jsou jednotlivé energetické hladiny velmi blízko u sebe, stačí nepatrný vliv elektrického pole k lomu, aby některé elektrony získaly potřebnou energii pro uspořádaný pohyb v makroskopickém měřítku. Látky, jejichž pásová struktura má charakter znázorněný na obr. 7.5a, respektive 7.5c, jsou tedy vodiče, zatímco látky s elektronovou strukturou uvedenou na obr. 7.5b jsou nevodiče. Periferní částečně zaplněný pás vodičů se nazývá vodivostním pásem. Nejbližší nižší (zcela zaplněný) pás se nazývá pásem valenčním.

Vedle krystalů existuje velké množství amorfních pevných látek, popř. látek s nedokonale vyvinutou krystalovou strukturou. Přesto, že v takových látkách nemohou být elektronové stavy popisovány tak jednoduše jako v krystalech, dovolené a zakázané pásy energií v nich existují a lokální hustota možných elektronových stavů je zpravidla určována lokálním uspořádáním. I v těchto látkách může být proud v principu realizován elektrony i děrami. Otázky elek­trické vodivosti různého typu látek budou podrobněji diskutovány v oddílu 7.3.

7.1.3 Elektronový plyn

Model elektronového plynu představuje velmi důležitou aproximaci pro popis chování nelokalizovaných (volných) elektronů v pevných látkách, zejména v kovech. Předpoklad o existenci volných elektronů v kovech první zavedl ně­mecký fyzik P. Drude v roce 1900, tedy krátce po objevu elektronu J. J. Thom­sonem (1897). Podle jeho představ existuje v kovu jistý počet elektronů, které jsou jen velmi volně vázány k jednotlivým atomům a které se uvnitř kovu cho­vají v prvním přiblížení jako molekuly ideálního plynu. Drude proto předpoklá­dal, že k popisu chování těchto volných elektronů je možné použít stejné statis­tické metody, které byly v té době s úspěchem používány pro vysvětlení mnohých vlastností plynů.

Situace volných elektronů v kovech je ovšem složitější než situace molekul v plynu, neboť kromě vzájemné interakce mezi elektrony, je nutné uvažovat interakci s ionty krystalové mřížky. Drudeho model předpokládá, že kladné čás­tice kompenzující záporný náboj volných elektronů v kovu, tj. ionty krystalové mřížky jsou mnohem těžší než elektrony a jsou v prvním přiblížení nehybné. Interakce každého volného elektronu s ionty krystalové mřížky a s jinými vol­nými elektrony je dána jen občasnými srážkami, které mají charakter pružných srážek. Při nich mění elektrony náhle směr svého pohybu a jejich prostřednic­tvím dochází také k výměně energie jednak mezi elektrony navzájem a jednak mezi elektrony a krystalovou mřížkou, takže tyto srážky umožňují ustavení ter­modynamické rovnováhy v kovu jako celku. V době mezi následujícími sráž­kami se elektrony pohybují zcela volně. V nulovém vnějším poli je jejich pohyb zcela neuspořádaný, takže střední hodnota rychlosti v libovolném směru je nulová.

Klasický model elektronového plynu předpokládá, že tento chaotický pohyb elektronů je možné popsat metodami klasické kinetické teorie plynů. Pro rozdě­lení rychlosti elektronů se tedy předpokládá platnost rozdělení Boltzmannova typu, takže hustota pravděpodobnosti f_B( v ) rychlosti v s danými složkami v  ℜ ≡  (v _x, v _y, v _z) je dána vztahem (viz například [10])

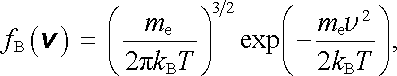(7.5)

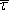ve kterém m_e značí hmotnost elektronu a k_B Boltzmannovu konstantu.[51] Dalším důležitým předpokladem modelu je možnost zavést střední dobu volného po­hybu elektronu mezi následujícími srážkami, o níž se předpokládá, že nezá­visí na poloze a rychlosti elektronu. Zavedeme-li střední rychlost elektronu 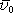, můžeme pak vyjádřit i střední volnou dráhu

.

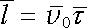(7.6)

V článku 7.6.5 uvidíme, že i když klasický model elektronového plynu předsta­vuje velmi hrubou aproximaci popisu volných elektronů, je schopen správně vyložit řadu vlastností kovů. Na druhé straně uvidíme, že v mnohých případech dává tento model výsledky, které jsou v rozporu s experimentem. Avšak přesto, že jsou dnes známá omezení jeho platnosti, zachovává si svůj význam přede­vším proto, že při své jednoduchosti dává v prvním přiblížení kvalitativně správnou a názornou představu o chování volných elektronů v kovech a vytváří východisko pro přesnější modely vycházející z kvantově mecha-nických zákonitostí.

Nejzákladnějším nedostatkem klasického modelu je, že Maxwellovo-Boltz­mannovo rozdělení nerespektuje Pauliho princip, který musí být při obsazování jednotlivých elektronových stavů respektován. Německý fyzik A. Sommerfeld odstranil tuto hlavní obtíž tím, že klasické rozdělení rychlostí nahradil kvantově mechanickým rozdělením Fermiho-Diracovým. Vytvořil tak nový model elek­tronového plynu a z něho vycházející další přiblížení elektronové teorie, která v mnohem větší míře vystihuje elektronové vlastnosti pevných látek.

Obr. 7.6 Průběh Fermiho-Diracova rozdělení.

Fermiho-Diracovo rozdělení určuje pravděpodobnost obsazení jednotlivých stavů v částečně zaplněném vodivostním pásu. Zvláště jednoduchá situace nastává při teplotě absolutní nuly, kdy je soustava v základním stavu s nejnižší možnou energií. Všechny stavy s energií menší než Fermiho energie E_F jsou plně obsazeny elektrony, zatímco stavy s energií vyšší jsou neobsazené (srov. obrázky 7.4 a 7.5). Pravděpodobnost p obsazení daného stavu je tedy buď jedna, nebo nula (viz obr. 7.6). Se vzrůstem teploty vzrůstá i energie elektronového plynu. Některé elektrony mohou získat vyšší kinetickou energii, takže přejdou do stavů nad Fermiho energií, naopak některé stavy s nižší energií se uprázdní. Pro pravděpodobnost p(E) obsazení stavu s kinetickou energií E = m_ev ²/2 lze odvodit výraz

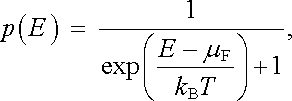(7.7)

ve kterém μ _F značí tzv. chemický potenciál. Při E = μ _F platí p(E)  = 1/2; pro nepříliš vysoké teploty lze u kovů položit μ _F = E_F. Obrázek 7.6 ukazuje vedle křivky pro T = 0 též průběh pravděpodobnosti p pro T = 0,1 E_F/k_B.

Vezme-li se v úvahu hustota možných stavů v okolí dané rychlosti v , je možné vyjádřit normovanou hustotu pravděpodobnosti f_F( v ) pro obsazení stavů v okolí dané rychlosti v . Platí pro ni vztah [52]

,

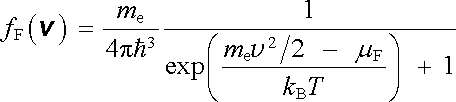(7.8)

který je analogií klasického vztahu (7.5) . Markantní rozdíl obou typů rozdělení je patrný z obr. 7.7, ve kterém jsou ve stejném měřítku vyneseny relativní změny f_B( v ) a f_F( v ) v závislosti na relativní hodnotě kinetické energie m_ev ²/2k_BT opět pro teplotu T = 0,1 E_F/k_B. Fermiho-Diracovo rozdělení přejde v klasické rozdě­lení typu (7.5) jen při dostatečně vysokých teplotách, kdy mají elektrony dosta­tečně velkou energii, takže platí (E - μ _F) >>  k_BT, a je tudíž možné ve jmenovateli (7.7) zanedbat první člen rovný jedné proti exponenciálnímu členu.

Obr. 7.7 Srovnání klasického a Fermiho-Diracova rozdělení.

7.1.4 Elektrické a magnetické momenty atomů a molekul

Atomy a molekuly jsou elektricky a magneticky aktivní útvary, a mohou tedy ve svém okolí vytvářet vlastní elektrické a magnetické pole. Pro jejich popis se nejčastěji používá multipólový rozvoj (srov. články 1.3.2 a 3.4.3), takže jsou charakterizovány hodnotami příslušných multipólových momentů, které tvoří parametry jednotlivých stacionárních stavů těchto atomů, respektive molekul.

Pro mnohé účely je plně dostačující charakterizovat danou soustavu prvním nenulovým členem multipólového rozvoje. V případě elektricky neutrálních atomů či molekul je tímto členem člen dipólový, charakterizovaný elektrickým dipólovým momentem p a magnetickým dipólovým momentem μ . Tyto mo­menty jsou dány vztahy, viz (1.146) a (3.110) ,

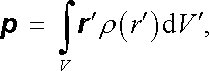v nichž ρ ( r ℜ' ) a j ( r ℜ' ) představují objemové hustoty náboje a proudu. Tyto hus­toty reprezentují "pohybový stav" jednotlivých nabitých částic v daném stacio­nárním stavu atomu či molekuly. Pro popis chování vyšetřovaných atomů či molekul v časově neproměnných (nebo pomalu proměnných) polích jsou pod­statné střední hodnoty uvedených dipólových momentů, k jejichž výpočtu musí být ovšem brány v úvahu kvantově mechanické zákonitosti.

Přesto, že oba dipólové momenty p a μ jsou dány zcela analogickými vztahy (1.146) a (3.110) , jsou v jejich vlastnostech podstatné rozdíly, neboť zatímco elektrický dipólový moment p je polární vektor, magnetický dipólový moment μ je vektor axiální (viz dodatek D l). Vektory p a μ se tedy chovají různě při ope­raci inverze. Z obecných kvantově mechanických vlastností elektronových stavů v atomu při operaci inverze plyne, že střední hodnota elektrického dipólového momentu volného atomu v nulovém vnějším elektrickém poli je vždy nulová. Tato vlastnost je důsledkem toho, že elektrony v atomu se pohybují ve středově symetrickém elektrickém poli jádra a snadno pochopíme i názorně, že těžiště elektronového náboje leží v těžišti náboje jádra.

Uvedená vlastnost však již nemusí obecně platit pro molekuly, u nichž obecně není zachována středová symetrie elektrického pole jader. Symetrické molekuly s nulovým dipólovým momentem se nazývají nepolárními, naopak molekuly s nenulovým dipólovým momentem polárními. Nejnázorněji si vznik dipólového momentu můžeme představit u dvouatomových molekul s iontovou vazbou. Molekulu tohoto typu můžeme v prvním přiblížení považovat za sou­stavu kladného a záporného iontu. Její dipólový moment je roven součinu ná­boje iontu a jejich vzájemné vzdálenosti. Mezi nepolární molekuly patří symet­rické dvouatomové molekuly jako H₂, N₂, O₂ a jiné, ze tříatomových molekul například oxid uhličitý CO₂. Jako příklady polárních molekul lze uvést oxid uhelnatý CO s dipólovým momentem p = 0,36.10^-30 C.m, dále chlorovodík HCl s dipólovým momentem p = 3,6.10^-30 C.m. Z tříatomových molekul má značně vysokou hodnotu dipólového momentu molekula vody H₂O, a to p = 6,13.10^-30 C.m.

Jiná situace nastává v případě magnetických momentů atomů, přičemž exis­tence vlastního magnetického momentu atomu souvisí s jeho vlastním momen­tem hybnosti. (Kvalitativně byly tyto otázky diskutovány již v článku 3.5.1, s poukazem na výsledky příkladů 3.4.6a a 3.4.6b.) Elektron ve stacionárním stavu s vedlejším kvantovým číslem l má orbitální moment hybnosti, jehož veli­kost a možné složky do daného směru jsou dány vztahy (7.2) a (7.3) . Orbitální magnetický moment elektronu v tomto stavu je určen gyromagnetickým pomě­rem γ _l  = e/2m_e (srov. příklad 3.4.6a). Velikost μ _l a možné složky magnetického momentu do daného směru μ _l,z jsou dány postupně vztahy

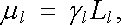(7.9)

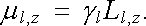(7.10)

S ohledem na vztahy (7.2) a (7.3) lze obě tyto veličiny vyjádřit pomocí Bohrova magnetonu (viz článek 3.5.1) a kvantových čísel l a μ _l . Platí

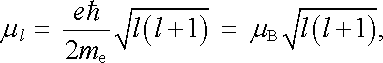(7.9a)

(7.10a)

Analogické vztahy platí i pro magnetický spinový moment elektronu, který je možné vyjádřit pomocí spinového gyromagnetického poměru γ _s  = e/m_e (viz opět článek 3.5.1). Využitím vztahů (7.4) můžeme opět vyjádřit velikost spinového magnetického momentu μ _s a jeho možné složky do daného směru μ _s,z pomocí Bohrova magnetonu a kvantových čísel s a m_s. Platí tedy

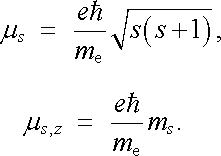(7.11)

Uvědomíme-li si, že s = 1/2, m_s = ℜ ± 1/2, vidíme že složky spinového magnetic­kého momentu do daného směru mohou nabývat jen hodnot ℜ ± μ _B.

V článku 7.1.1 jsme viděli, že zcela zaplněné atomové podslupky mají nu­lový orbitální i spinový moment hybnosti. Podle právě uvedených vztahů mají tyto podslupky i nulový magnetický dipólový moment. Volný atom obsahující jen zcela zaplněné nebo zcela prázdné podslupky má tedy nulový celkový vlastní magnetický moment. V principu mohou existovat dva typy atomů s částečně zaplněnými podslupkami, a tedy s nenulovým magnetickým momen­tem, a to buď atomy s částečně zaplněnou periferní podslupkou, nebo tzv. pře­chodové atomy s částečně zaplněnou některou vnitřní podslupkou. Jako příklady prvního typu mohou sloužit již zmíněné atomy vodíku a sodíku. Mezi nejzná­mější reprezentanty atomů druhého typu patří prvky skupiny železa (Sc, Ti, V, Cr, Mn, Co, Ni) s částečně zaplněnou podslupkou 3d nebo prvky vzácných ze­min (Ce, Pr, Nd,...) s částečně zaplněnou podslupkou 4f.

Orbitální a spinové magnetické momenty elektronů nezaplněných podslupek se skládají podle pravidel plynoucích z kvantové mechaniky. Výsledný magne­tický moment atomu je pak opět v relaci s jeho celkovým momentem hybnosti. Možné hodnoty složky magnetického momentu atomu do daného směru mohou mít řádovou velikost jednotek Bohrova magnetonu μ _B.

Nakonec ještě připomínáme, že všechny úvahy tohoto článku se týkaly jen vlastních momentů volných atomů, respektive molekul. Ve vnějších elektric­kých či magnetických polích dochází ke změnám v elektronových stavech, čímž vznikají dodatečné indukované momenty. Podobné procesy nastávají i u volných elektronů, tedy u elektronového plynu. Některé elementární úvahy o podobných otázkách budou uvedeny v oddílech 7.2 a 7.6, v následujícím textu této kapitoly však budeme uvažovat jen výsledný příspěvek atomů či molekul k makroskopic­kému poli v látce. Střední hodnotu magnetického momentu připadající na atom či molekulu budeme považovat za klasickou vektorovou veličinu ve smyslu oddílu 3.4 a budeme ji označovat symbolem m .

---

---