---

---

3.4 Magnetický dipól

Pro popis vlastností magnetického pole je pojem magnetického dipólu neméně důležitý jako pojem elektrického dipólu pro popis pole elektrostatického. Mag­netickým dipólem se budeme zabývat nyní. Postup výkladu budeme přitom volit tak, aby byly zdůrazněny analogie i odlišné vlastnosti mezi dipólem elektrickým a magnetickým (srov. oddíl 1.3).

3.4.1 Magnetický dipólový moment rovinné proudové smyčky

Uvažujme rovinnou proudovou smyčku l libovolného tvaru a malých rozměrů, protékanou proudem I, kterou umístíme do blízkosti počátku pravoúhlé soustavy souřadné. Budeme studovat magnetické pole této smyčky v bodě r značně vzdáleném od počátku soustavy souřadné (viz obr. 3.23). Vektorový potenciál A (r ) smyčky bude zřejmě dán výrazem typu (3.82) , ve kterém R  = r  - r ℜ' . Polo­hový vektor r ℜ' přitom probíhá body smyčky, takže podle uvedeného předpokladu platí rℜ'  <<  r a v prvním přiblížení lze položit R   r. Výraz pro vektorový potenciál lze využitím (D 1.73) vyjádřit pomocí plošného integrálu

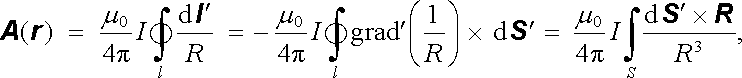(3.101)

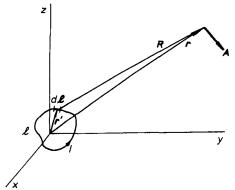
v němž se integruje přes část roviny S ohraničené smyčkou l a symbolem gradℜ' je vyznačeno, že se tato operace vztahuje na proměnnou r'. Použijeme-li již uvedené přiblížení, nebude integrovaná funkce záviset na integrační proměnné r' a vektorový potenciál bude možné přibližně vyjádřit vztahem

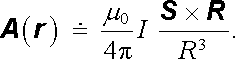(3.102)

Tento vzorec je možné zapsat v obvyklejším tvaru

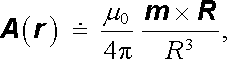(3.103)

zavedeme-li veličinu m  = IS , kterou nazveme Amp`erovým magnetickým momentem smyčky[24] .

Magnetickou indukci vyjádříme vztahem B  = rot A . Přímý výpočet lze provést využitím identity vektorové analýzy (D 1.55) pro rotaci vektorového sou činu dvou funkcí. Jelikož m je konstanta a pro r ℜ ≠  0 platí 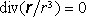, dostaneme

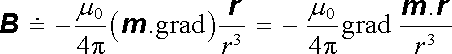a po provedení naznačené operace získáme konečný výsledek

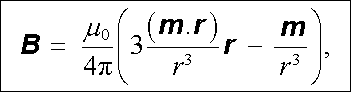(3.104)

který je formálně shodný s výrazem (1.125) pro intenzitu pole elektrického di­pólu. Průběh siločar elektrického pole konečného dipólu a indukčních čar ko­nečného magnetického dipólu je ve velkých vzdálenostech stejný (viz obr. 3.24).

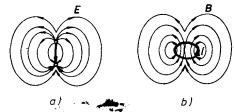
Uvedená shoda je pozoruhodná zejména proto, že jsme k výrazům pro pole di­pólu dospěli zásadně odlišným způsobem. Zatímco elektrický dipól je reprezen­tován dvojicí bodových nábojů stejné velikosti a opačného znamení, magnetický dipól je tvořen smyčkou protékanou proudem. Díky shodě v průběhu polí je možné formálně zavést pojem magnetického náboje a magnetický dipól chápat také jako dvojici magnetických nábojů stejné velikosti a opačného znamení. Takový postup se někdy volí pro popis magnetického pole vytvořeného jen zmagnetovanými látkami. Příslušná teorie je pak zcela analogická teorii elektro­statického pole (viz článek 3.5.6). Na rozdíl od elektrostatiky je však nutné po­važovat magnetické náboje za formálně zavedenou veličinu (srov. články 3.3.3 a 3.4.4).

Podobně jako v případě elektrického dipólu můžeme i zde zavést pojem ele­mentárního (bodového) magnetického dipólu, budeme-li rozměry smyčky zmen­šovat k nule a měnit proud I tak, aby magnetický moment měl konečnou nenulo­vou limitní hodnotu. Vzniklý bodový útvar bude charakterizován momentem m . Při jeho umístění v počátku soustavy souřadné budou vzorce (3.103) a  (3.104) popisovat průběh magnetického pole přesně ve všech bodech r ℜ ≠  0. Je zřejmé, že pro případ elementárního magnetického dipólu ztrácí konkrétní smysl otázka, je-li tvořen "bodovým" proudovým útvarem, či "nekonečně blízkými" mag-netickými náboji. Pole elementárního magnetického dipólu lze též popsat pomocí skalárního potenciálu (viz článek 3.4.4).

3.4.2 Potenciální energie a silové účinky magnetického pole na magnetický dipól

Uvažujme uzavřenou proudovou smyčku protékanou proudem I vloženou do vnějšího magnetického pole indukce B . Smyčku posuňme do nové polohy při zachování proudu I. Posunutí nechť je velmi malé a nechť je charakterizováno vektorem Δ a (viz obr. 3.25). (Vektor Δ a nemusí být podél celé smyčky kon­stantní; dokonce není ani nutné předpokládat, že smyčka si při posunutí zachová svůj tvar.)

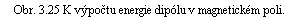
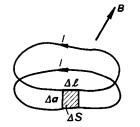
Na smyčku v magnetickém poli působí síla F , kterou je možné vypočítat pomocí vztahu (3.58) a která při posunutí smyčky vykoná mechanickou práci A. Velikost práce Δ A připadající na malý úsek vodiče Δ l bude zřejmě dána vztahem

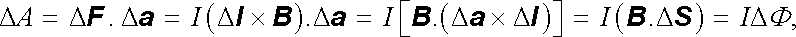v němž Δ S je plocha opsaná úsekem vodiče Δ l při posunutí o Δ a . Celkovou práci A vypočítáme integrací předchozího vztahu podél celé smyčky. Označíme-li Φ ₁, Φ ₂ magnetické toky tekoucí smyčkou v její výchozí a konečné poloze, bude podle obr. 3.25 s ohledem na rovnici (3.72) zřejmě platit

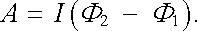(3.105)

Práce bude tedy kladná, když tok poroste a naopak bude záporná, bude-li tok klesat. Magnetické síly mají tudíž tendenci vtahovat smyčku do magnetického pole tak, aby magnetický tok jí protékající byl co největší. Veličina IΦ předsta­vuje práci, kterou magnetické síly vykonají při přenesení smyčky z místa o nu­lovém toku do místa o toku Φ . Veličinu

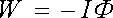(3.106)

můžeme tedy považovat za potenciální energii smyčky v magnetickém poli.

Pro rovinnou smyčku malých rozměrů o ploše S můžeme psát Φ  = B .S a po zavedení jejího magnetického momentu m  = IS dostaneme výraz pro potenciální energii ve tvaru

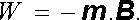(3.107)

Tento vztah má stejný tvar jako výraz (1.131) pro energii elektrického dipólu v elektrostatickém poli. Podle toho, co bylo o magnetickém dipólu řečeno v předchozím článku, udává výraz (3.107) zřejmě energii obecného (elementár­ního) bodového dipólu v libovolném vnějším magnetickém poli. Díky formální totožnosti (3.107) s (1.131) je možné využitím (1.133) získat (stejným postupem jako v případě elektrického dipólu) analogické výrazy pro složky zobecněné síly působící na magnetický dipól v magnetickém poli. Například při popisu sou­stavy pomocí pravoúhlých souřadnic dostaneme pro obyčejnou sílu F a moment silové dvojice M

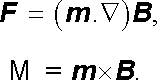(3.108)

3.4.3 Multipólový rozvoj magnetického pole

Nyní budeme vyšetřovat magnetické pole obecnějšího útvaru, než je rovinná proudová smyčka. Budeme předpokládat libovolné rozložení proudu j (r ℜ' ), bu­deme však požadovat, aby proudová hustota byla nenulová pouze uvnitř koule K poloměru R₀ se středem v počátku soustavy souřadné. Uvažované proudy se tedy v objemu K uzavírají. Průběh pole budeme opět vyšetřovat v obecném bodě r značně vzdáleném od počátku soustavy, takže opět můžeme předpokládat R₀ <<  r.

Vektorový potenciál A (r ) bude dán vztahem typu (3.80) , přičemž se integruje přes objem V celý uzavřený uvnitř koule K. Za předpokladu rℜ'  <<  r lze vektorový potenciál přibližně vyjádřit v konkrétnějším tvaru, rozvineme-li veličinu 1/R v mocninnou řadu souřadnic vektoru r ℜ' kolem počátku soustavy souřadné. Stej­ným postupem, který byl použit pro multipólový rozvoj skalárního elektrostatic­kého potenciálu v oddílu 1.3, získáme pro první tři členy rozvoje vektorového potenciálu výraz

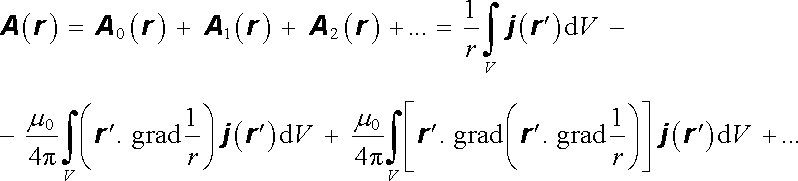(3.109)

První člen A ₀(r ) v rozvoji (3.109) je roven nule, neboť integrál z proudové hus­toty j (r ℜ' ) přes objem V, ve kterém se všechny uvažované proudy uzavírají, je nulový.

První nenulový člen rozvoje je obecně A ₁(r ). Aproximuje vyšetřované pole v prvním přiblížení, a má tedy dominantní význam. Vyšetříme proto podrobněji jeho vlastnosti. Vektorový potenciál je možné vyjádřit ve tvaru (3.103) pro bo­dový magnetický dipól,

,

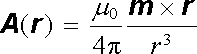(3.103a)

jestliže zobecníme definici (Amp`erova) magnetického momentu (srov. čl. 3.4.1) pomocí vztahu

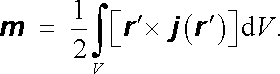(3.110)

Lze se snadno přesvědčit (srov. čl. 3.3.3), že pro speciální případ úzké rovinné proudové trubice malých rozměrů se vztah (3.110) redukuje na jednoduchý vý­raz m  = IS zavedený v čl. 3.4.1. Odpovídající průběh vektoru magnetické in­dukce pro dipólový člen je zřejmě dán vztahem (3.104) .

Je-li dipólový člen rozvoje nulový, nebo je-li dané obecné pole třeba popsat s větší přesností, je nutné vzít v úvahu kvadrupólový, popř. další členy. V tomto směru je situace zcela analogická elektrostatickému poli (srov. článek 1.3.2). Platí zejména také, že velikost jednotlivých příspěvků rozvoje je závislá na symetrii rozložení proudu. Se zvyšováním této symetrie klesá podíl příspěvků vyšších multipólů. (Jejich velikost navíc rychle klesá s rostoucí vzdáleností.) Osově symetrické rozložení proudu vytváří magnetické pole, jehož průběh se nejvíce blíží poli dipólu.

3.4.4 Objemové rozložení magnetických dipólů

Stejně jako v případě elektrických dipólů (viz článek 1.3.4) můžeme uvažovat spojité prostorové rozložení magnetických dipólů, charakterizované (objemo­vou) hustotou (například Amp`erova) dipólového momentu M (r ). Tato veličina se nazývá vektorem magnetizace[25] (srov. čl. 3.5.2). Celkový dipólový moment m _V daného objemu V lze pak vyjádřit objemovým integrálem

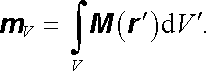(3.112)

Vektorový potenciál magnetického pole těmito dipóly vytvořeného bude podle (3.103) zřejmě dán vztahem

.

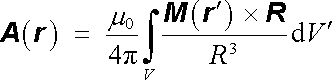(3.113)

Tento výraz lze upravit na přehlednější tvar, přepíšeme-li integrand následujícím způsobem

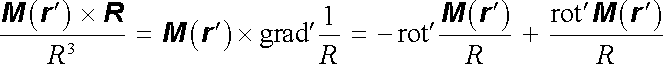a použijeme-li zobecněné Gaussovy věty (D 1.72), dostaneme tak výsledek

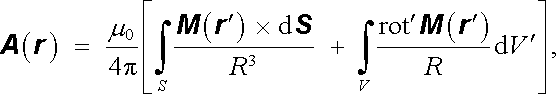(3.114)

v němž S je uzavřená plocha ohraničující objem V a čárkou u operací "grad" a "rot" je naznačeno, že se tyto operace vztahují na integrační proměnnou r  ℜ' . Jestliže položíme

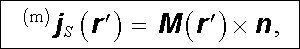(3.115)

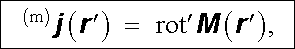(3.116)

kde n je jednotkový vektor vnější normály plochy S, můžeme vztah (3.114) dále vyjádřit ve tvaru

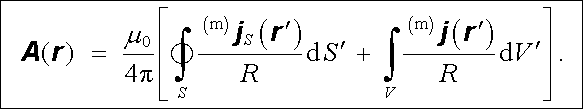(3.117)

Srovnáním posledního vztahu s (3.80) a (3.80a) můžeme učinit zajímavý závěr: Magnetické pole vytvořené prostorovým rozložením magnetických dipólů s ob­jemovou hustotou M (r ℜ' ) v objemu V je totožné s magnetickým polem vytvořeným objemovými proudy hustoty ^(m)j (r ℜ' ) (3.116) tekoucími v objemu V a plošnými proudy hustoty ^(m)j _S(r ℜ' ) (3.115) tekoucími na ploše S ohraničující objem V.

Průběh magnetické indukce studovaného pole získáme aplikací operace ro­tace na vektorový potenciál daný některými z výrazů (3.113) , (3.114) , (3.117) . Díky formální shodnosti výrazů (1.125) a (3.104) pro intenzitu a magnetickou indukci pole elektrického a magnetického dipólu a vzhledem k platnosti principu superpozice pro oba typy polí lze soudit, že při shodném prostorovém rozložení objemové hustoty elektrického dipólového momentu P (r ℜ' ) (viz čl. 1.3.4) a obje-mové hustoty magnetického dipólového momentu M (r ℜ' ) získáme pole o shod-ném průběhu elektrické intenzity a magnetické indukce.

Uvedená shoda dovoluje učinit druhý zajímavý závěr: Jelikož elektrostatické pole je potenciální, je možné i pole elementárního magnetického dipólu, respek­tive pole prostorově rozložených magnetických dipólů, popsat pomocí skalárního potenciálu. Skutečně, zavedeme-li analogicky k (1.169) formálně objemovou a plošnou hustotu "magnetického náboje" ρ _m(r ℜ' ) a σ _m(r ℜ' ) vztahy

(3.118)

je možné zavést skalární magnetický potenciál φ _m(r ) analogicky k (1.169) vý­razem

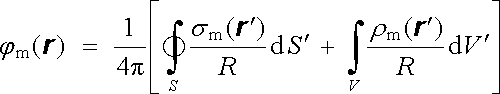(3.119)

a magnetickou indukci B (r ) studovaného pole v bodech s nulovou magnetizací vyjádřit jako

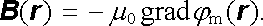(3.120)

Speciálně pole jediného elementárního dipólu s dipólovým momentem m bude popsáno skalárním potenciálem ve tvaru

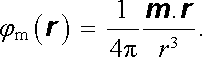(3.121)

3.4.5 Magnetická dvojvrstva

Vedle objemového rozložení magnetických dipólů, probíraného v předchozím článku, je možné uvažovat i magnetické dipóly spojitě rozložené na dané ploše S. Plošné rozložení magnetických dipólů se nazývá magnetickou dvojvrstvou (srov. pojem elektrické dvojvrstvy zavedený v čl. 1.3.3) a je charakterizováno plošnou hustotou magnetického dipólového momentu M _S(r ℜ' ). Celkový moment rozložený na dané ploše S je zřejmě roven plošnému integrálu

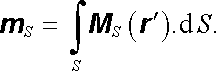(3.122)

Magnetická dvojvrstva, jejíž hustota dipólového momentu má všude stejnou velikost a je v každém bodě orientována ve směru normály plochy, se nazývá homogenní. Nadále se budeme zabývat jen vlastnostmi homogenní dvojvrstvy.

Za předpokladu platnosti principu superpozice lze vektorový potenciál magnetického pole dvojvrstvy vyjádřit užitím (3.103) ve tvaru plošného inte­grálu

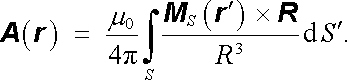(3.123)

Využitím (D 1.73) lze tento výraz pro homogenní dvojvrstvu vyjádřit pomocí křivkového integrálu přes křivku l, ohraničující plochu S. Platí

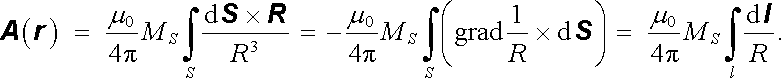(3.124)

Srovnáním výsledku s (3.82) vidíme, že výraz pro vektorový potenciál dvojvrs­tvy se ztotožní s výrazem pro vektorový potenciál magnetického pole velmi tenké uzavřené proudové smyčky, bude-li její proud I roven velikostí plošné hustotě dipólového momentu dvojvrstvy. Tedy

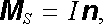(3.125)

kde n je jednotkový vektor normály plochy S v daném bodě.

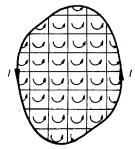
Z uvedeného výsledku vyplývá, že homogenní magnetická dvojvrstva vytvoří v okolním prostoru stejné magnetické pole jako velmi úzká uzavřená proudová trubice ohraničující plochu dvojvrstvy, jestliže proud tekoucí trubicí splňuje podmínku (3.125) . Ekvivalenci dvojvrstvy a proudové smyčky snadno názorně pochopíme podle obr. 3.26. Jednotlivé magnetické dipóly homogenní dvojvrstvy jsou v obrázku reprezentovány smyčkami protékanými proudem I. Tyto proudy sousedních smyček se však v celé ploše vzájemně vyruší. Nevyrušen zůstane jen proud na obvodu dvojvrstvy, který reprezentuje zmíněnou proudovou trubici.

Díky formální shodnosti výrazů (1.125) a (3.104) pro intenzitu a magnetic­kou indukci elektrického a magnetického dipólu je možné magnetické pole ho­mogenní magnetické dvojvrstvy vyšetřovat též způsobem, který byl v článku 1.3.3 použit pro dvojvrstvu elektrickou. Podobně jako v případě objemově roz­ložených magnetických dipólů je i zde zřejmé, že pole magnetické homogenní dvojvrstvy lze popsat skalárním magnetickým potenciálem φ _m(r ). V analogii se vztahem (1.158) dostaneme pro tento potenciál výraz

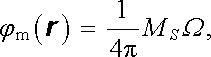(3.126)

kde Ω značí prostorový úhel, pod nímž je plocha dvojvrstvy vidět z bodu r, v kterém potenciál uvažujeme. Magnetická indukce B (r ) může pak být vypo-čtena podle (3.120) . Potenciál φ _m(r ) je spojitý všude, s výjimkou plochy dvoj-vrstvy S. Při průchodu touto plochou má nespojitost M_S .

3.4.6 Řešené příklady

a) Magnetický dipólový moment nabité částice konající rovnoměrný kruhový
pohyb

Uvažujme bodovou částici hmotnosti M₀ nesoucí náboj q, která koná rovno­měrný kruhový pohyb rychlostí v po dráze o poloměru r. Je zřejmé, že částice reprezentuje proudovou smyčku o ploše S = ², s proudem I = qv/2π r. Její mag­netický dipólový moment m má podle článku 3.4.1 velikost

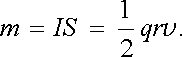(3.127)

Sledovaná částice reprezentuje také mechanickou soustavu, jejíž pohybový stav je možné charakterizovat hodnotou mechanického momentu hybnosti L . Pro jeho velikost platí

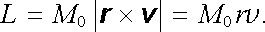Vypočítáme-li poměr velikosti magnetického momentu m a mechanického mo­mentu hybnosti částice L, dostaneme tzv. gyromagnetický poměr γ . Pro vyšetřo­vanou částici vychází

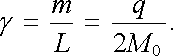(3.128)

Z výsledku můžeme učinit zajímavý závěr: gyromagnetický poměr je pro danou částici charakteristickou konstantou, která nezávisí na jejím pohybovém stavu.

b) Magnetický dipólový moment rotující nabité koule

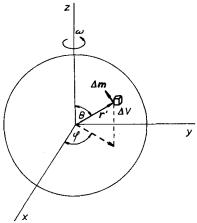
Určeme magnetický dipólový moment homogenně nabité koule s objemovou hustotou náboje ρ , která rotuje úhlovou rychlostí ω kolem osy z. Pro výpočet magnetického dipólového momentu použijeme vztah (3.110) . Uvědomíme si, že pro ρ  >  0 má výsledný moment směr vektoru úhlové rychlosti a že diferenciál dipólového momentu dm (viz obr. 3.27) přispěje jen složkou do osy z; dm  sinϑ . Stačí tudíž integrovat jen přes velikost této složky. Vektory j a r ℜ' jsou navzájem kolmé, přičemž platí j = ρ v , v  = r ℜ' ω sinϑ . Tedy

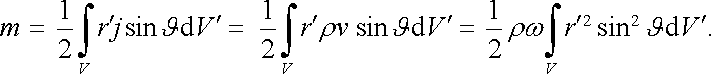Ve sférických souřadnicích dostaneme

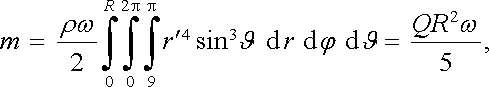(3.129)

kde jsme symbolem Q označili celkový náboj koule .

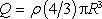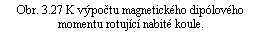
Analogicky k předchozímu příkladu vypočítáme gyromagnetický poměr rotu­jící koule. Její hmotnost označíme M₀ a vezmeme v úvahu, že její moment hyb­nosti L je roven L = (2/5)M₀R²ω . Dostaneme výsledek shodný s (3.128) , který potvrzuje závěr předchozího příkladu.

---

---