Již v úvodu oddílu 3.3 bylo zdůrazněno, že k výslednému magnetickému poli v daném bodě mohou kromě makroskopických proudů přispívat také zmagnetované látky. Byly rovněž uvedeny některé experimentální údaje, které ukazují, že magnetické pole může existovat i bez přítomnosti makroskopických proudů. Vektor magnetické indukce byl v článku 3.3.1 definován vztahy (3.57) , respektive (3.58) . Jak bylo na uvedeném místě zdůrazněno, platí tato definice obecně, bez ohledu na to, jakými zdroji je magnetické pole vybuzeno a jde-li o magnetické pole ve vakuu či v látkovém prostředí. (Pole v látkovém prostředí zde ovšem opět chápeme makroskopicky, podobně jako v oddílu 1.5 pole elektro-statické.)
Přesto, že se v této kapitole zabýváme fenomenologickým popisem magnetických jevů z makroskopického hlediska, bude pro získání větší názornosti užitečné uvést zpočátku alespoň kvalitativně některá nejzákladnější fakta o magnetických vlastnostech atomů a molekul.
Každý atom, jako soustava vzájemně se pohybujících nabitých částic, je také magneticky aktivní. Elektron obíhající kolem jádra můžeme považovat za proudovou smyčku a jeho magnetické účinky můžeme charakterizovat příslušným magnetickým momentem (srov. příklad 3.4.6a). Kromě toho je dnes dostatečně prokázáno, že některé elementární částice samotné (elektron, proton, neutron) mají vlastní magnetický moment. Jedním ze základních rysů magnetismu elementárních částic a atomů je přímá souvislost mezi magnetickým momentem an> a momentem hybnosti L . Mezi oběma momenty platí vždy přímá úměrnost charakterizovaná gyromagnetickým poměrem γ , an> = γ L . (Souvislost mezi magnetickým dipólovým momentem a mechanickým momentem hybnosti není ovšem omezena jen na mikroskopické objekty - srov. příklady 3.4.6a a 3.4.6b). Části-ce, která má od nuly různý magnetický moment, má tedy vždy nenulový i mecha-nický moment hybnosti a charakter jejího pohybu ve vnějším magnetickém poli je vždy do určité míry podobný pohybu setrvačníku. Jak uvidíme v kapitole 7, je tato okolnost podstatná pro chování látek ve stacionárním i časově proměnném magnetickém poli. Momenty, které získává elektron v důsledku svého pohybu kolem jádra, se nazývají orbitálními momenty. Vlastní moment hybnosti elementárních částic (elektronů, nukleonů apod.) se nazývá jejich spinem. Spinu příslušný magnetický moment se nazývá spinovým magnetickým momentem.
Z kvantové mechaniky víme, že moment hybnosti orbitálního pohybu elektronu v atomu je kvantován a jeho složka do daného směru může nabývat pouze hodnot, které jsou celistvým násobkem veličiny h = h/2e h B 6,626.10-34 J.s je Planckova konstanta . Podle (3.128) je tedy kvantován i příslušný magnetický moment. Nejmenší orbitální magnetický moment elektronu odpovídá nejmenší nenulové hodnotě orbitálního momentu hybnosti, která je rovna h, a nazývá se Bohrův magneton B. Podle (3.128) platí
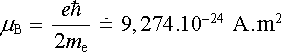 . . |
Z kvantové mechaniky dále plyne, že i spinový magnetický moment elektronu může mít v daném směru velikost rovnou B, gyromagnetický poměr má však v tomto případě hodnotu γ s = e/me. Magnetické dipólové momenty nukleonů a jader se vyjadřují pomocí analogické veličiny N, zvané jaderný magneton. Platí pro něj
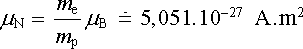 , , |
kde mp je hmotnost protonu. Podrobněji je o této problematice pojenáno v čl. 7.1.4 a v Dodatku 2.
Výsledný magnetický moment atomu (a tedy i jeho chování ve vnějším magnetickém poli) je dán vektorovým součtem magnetických momentů jednotlivých jeho složek. Výsledný magnetický moment elektronového obalu má řádovou velikost Bohrova magnetonu, magnetické momenty jader jsou obecně o tři řády menší a mohou být v prvním přiblížení zanedbány. Hodnota výsledného magnetického momentu závisí samozřejmě na stavech, v nichž se jednotlivé elektrony nacházejí. Výsledný moment může být nulový i v případě, kdy atom či molekula obsahuje značný počet elektronů, a naopak může být od nuly různý pro velmi jednoduché atomy či molekuly. Jeho hodnota závisí také na chemických faktorech, takže atom daného prvku může mít různý magnetický moment v různých typech sloučenin. Specificky složitá je situace zejména v případě kovů, v nichž existují volné (vodivostní) elektrony, které jsou společné všem atomům kovu.
U většiny látek jsou atomové momenty za nepřítomnosti vnějšího magnetického pole orientovány chaoticky, takže výsledný magnetický moment makroskopického množství látky je roven nule. Teprve při vložení do vnějšího magnetického pole působí na atomové magnetické momenty moment síly (3.108) , který se snaží orientovat je do směru pole. Látka pak jeví nenulový makroskopický magnetický moment; říkáme, že je zmagnetována. (Kromě uvedeného orientačního mechanismu může vnější pole také ovlivňovat stavy elektronů v atomu, a tím ovlivňovat i magnetické momenty jednotlivých atomů.)
Právě uvedená fakta ukazují, že lze každému atomu či molekule dané látky připsat určitou střední hodnotu magnetického momentu p m = 0m , který je jednoznačně určen fyzikálním stavem látky a uplatní se v jejích makroskopických projevech. V dalším textu této kapitoly se budeme již výhradně zabývat tímto makroskopickým popisem magnetického pole a budeme vycházet jen z právě uvedeného kvalitativního poznatku. Všechny otázky podmíněné konkrétními vlastnostmi a mikrofyzikální strukturou atomu ponecháme stranou. Pozornost jim bude věnována v kapitole 7.
Z toho, co bylo řečeno, vyplývá, že magnetické pole vytvořené zmagnetovanými látkami je možné považovat za magnetické pole soustavy prostorově rozložených dipólů. Jak bylo ukázáno v článku 3.4.4, je průběh tohoto pole jednoznačně určen charakterem prostorového rozložení dipólů. Podobně jako v případě elektrostatického pole (viz oddíl 1.5) v látkovém prostředí, je i zde výhodné použít vektorovou funkci polohového vektoru, která popisuje v makroskopickém měřítku zmíněné parametry atomových dipólů. Mluvíme o magnetické polarizaci P m(r ), respektive o magnetizaci M (r ) dané látky (srov. čl. 3.4.4). Vektor P m, respektive M vyjadřuje magnetický moment připadající na její jednotkový objem. V případě magnetické polarizace jde o moment Coulombův, v případě magnetizace o moment Amp`erův. Platí tedy vztah (3.111)
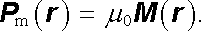 |
Definiční vztahy pro magnetickou polarizaci (magnetizaci) jsou zcela analogické příslušným vztahům pro polarizaci elektrickou (viz články 1.3.4 a 1.5.2). Uvedeme proto jen jejich velmi stručný přehled. Uvažujme malý objem Δ V vyšetřované látky, který je však dostatečně velký, aby z makroskopického hlediska mohly být zanedbány fluktuace magnetického momentu na vzdálenostech srovnatelných s rozměry atomu a tento objem mohl být považován za kontinuum. Jeho magnetický moment p m,Δ V může být potom vyjádřen dvěma způsoby: jednak jako součet momentů p m,i jednotlivých atomů
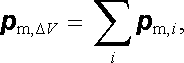 |
(3.130) |
jednak po zavedení limitní veličiny (magnetické polarizace)
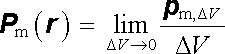 |
(3.131) |
ve tvaru
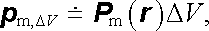 |
přičemž polohový vektor r může být v objemu Δ V zvolen libovolně. Magnetický moment p m,Δ V libovolného objemu V, je zřejmě možné vyjádřit ve tvaru objemového integrálu
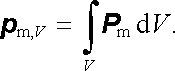 |
(3.132) |
Ve speciálním případě, kdy je magnetická polarizace v celém objemu homogenní, platí
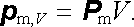 |
(3.133) |
Pro magnetizaci lze napsat analogické výrazy
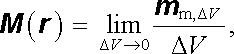 |
(3.131a) |
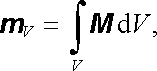 |
(3.132a) |
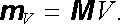 |
(3.133a) |
Rozměr magnetické polarizace je shodný s rozměrem magnetické indukce. Její jednotkou v Mezinárodní soustavě je tesla (T). Jednotkou magnetizace je ampér na metr (A.m-1).
V článku 3.4.1 jsme zavedli pojem bodového magnetického dipólu při studiu magnetického pole proudové smyčky. Z druhé strany je jasné, že magnetické pole každého dipólu je možné (bez ohledu na jeho vnitřní strukturu) reprezentovat magnetickým polem proudové smyčky stejného magnetického momentu. Uvedené skutečnosti umožňují vyjádřit magnetické pole zmagnetovaného tělesa (jež je polem soustavy dipólů) pomocí magnetického pole proudových smyček. Právě získaný výsledek vyjadřuje v podstatě hypotézu o existenci molekulárních proudů, kterou zavedl A. M. Amp`ere, když předpokládal, že příčinou magnetické aktivity látek jsou mikroskopické proudy, které se uzavírají v molekulárních rozměrech.
Úvahy tohoto druhu lze dále rozvíjet, když si uvědomíme, že soustava "molekulárních" proudových smyček může reprezentovat i určité makroskopické proudy.
Vznik takových proudů lze kvalitativně pochopit z obr. 3.28a, který je analogický s obr. 3.26 (objasňujícímu ekvivalenci proudové smyčky a magnetické dvojvrstvy) a který schematicky znázorňuje řez zmagnetovaným tělesem s magnetizací kolmou k rovině nákresny. Plochu řezu si můžeme představit rozdělenou na malé plošky, z nichž každá reprezentuje proudovou smyčku, po jejímž obvodu protéká "molekulární proud" Imol. Je zřejmé, že pokud budou proudy ve všech smyčkách stejné, budou se vzájemně rušit ve společných stranách sousedících smyček a nezrušeny zůstanou pouze proudy na povrchu tělesa. Lze tedy soudit, že magnetické pole vytvořené homogenně zmagnetovaným tělesem bude totožné s polem vhodně zvolených makroskopických plošných proudů tekoucích po povrchu tělesa. Největší hustotu budou mít zřejmě v místech, kde je povrch rovnoběžný s vektorem magnetizace, a naopak v místech, kde je povrch k magnetizaci kolmý, bude jejich hustota nulová.
Nebudou-li proudy ve všech smyčkách uvnitř tělesa stejné, nebudou se vzájemně rušit a uvnitř tělesa budou moci vznikat objemové makroskopické proudy. (Na obrázku je tato situace reprezentována jednou chybějící smyčkou.) Lze tedy říci, že objemové makroskopické proudy mohou reprezentovat nehomogenity v magnetizaci těles.
Na základě právě uvedených úvah lze očekávat, že magnetické pole libovolného zmagnetovaného tělesa bude možné také vyjádřit jako pole makroskopických plošných proudů tekoucích na povrchu tělesa a makroskopických objemových proudů tekoucích uvnitř tělesa. Tyto proudy se nazývají magnetizačními proudy a mají charakter efektivních vázaných proudů, o nichž byla řeč v článku 3.1.2.

Obr. 3.28 K výkladu souvislosti magnetizačních proudů s nehomogenitou magnetizace.
Vyjádření magnetického pole zmagnetovaného tělesa pomocí pole magnetizačních proudů má výhodu v tom, že dovoluje použít všechny vztahy platné pro pole makroskopických proudů ve vakuu také pro popis magnetického pole zmagnetovaných těles. V tomto smyslu je zde plná analogie s elektrostatikou (viz oddíl 1.5), kde je také možné vyjádřit elektrostatické pole zpolarizovaných těles (tj. pole soustavy elektrických dipólů) pomocí pole vázaných nábojů. Avšak zatímco vázané náboje jsou reálně existující makroskopickou veličinou, v případě vázaných magnetizačních proudů tomu tak není. Tyto proudy nemají nic společného se skutečnými kondukčními či konvekčními proudy, tj. s přemisťováním nábojů v makroskopickém měřítku. Mohou být od nuly různé jak ve vodivém, tak i v nevodivém prostředí a představují jen efektivní veličinu umožňující pohodlně popsat magnetismus zmagnetovaných těles.
Právě zmíněná možnost vyjádření magnetického pole zmagnetovaných těles pomocí magnetického pole vázaných magnetizačních proudů je ovšem podmíněna nalezením takového rozložení proudů, o kterém bude předem známo, že vytvoří stejné magnetické pole jako zmagnetované těleso. Tato otázka však již byla bez ohledu na právě provedené názorné úvahy v podstatě vyřešena v článku 3.4.4. Ze vztahů (3.114) a (3.117) vyplynul z požadavku ekvivalence obou způsobů vyjádření vztah mezi magnetizací M (r ) a hustotami plošných magnetizačních proudů (m)j S(r ) (3.115) a objemových magnetizačních proudů (m)j (r ) (3.116)
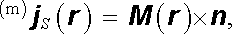 |
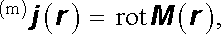 |
kde n je jednotkový vektor normály na povrchu zmagnetovaného tělesa. Zdůrazněme znovu, že plošné magnetizační proudy jsou nenulové na povrchu těchto těles a objemové magnetizační proudy jsou nenulové uvnitř těles.
Výraz (3.116) je možné bez obtíží převést na integrální tvar, neboť výsledný magnetizační proud (m)I protékající libovolnou plochou S je dán vztahem
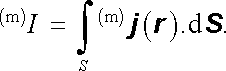 |
Použitím Stokesovy věty je možné příslušný plošný integrál převést na křivkový integrál přes křivku l ohraničující plochu S. Platí tedy
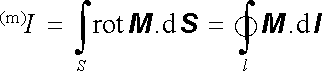 . . |
(3.116a) |
Připomínáme (viz Dodatek 1), že orientací plochy S, která je nezbytná pro stanovení znamení proudu, je určena i orientace křivky l ve vztahu (3.116a) .
Vztahy (3.115) a (3.116) lze získat i matematicky jednodušším elementárním (i když méně rigorózním) postupem. Budeme nejdříve uvažovat situaci na povrchu zmagnetovaného tělesa o magnetizaci M , jehož část je zobrazena na obr. 3.28b. Předpokládejme, že na tomto povrchu teče plošný magnetizační proud reprezentovaný hustotou (m)j S(r ). Zvolme úzkou orientovanou obdélníkovou plošku, jejíž delší strany Δ V jsou rovnoběžné s jednotkovým tečným vektorem t a jejíž plocha protíná povrch tělesa v kolmém směru (viz obr. 3.28b). Celkový proud protékající touto ploškou můžeme počítat dvěma způsoby: za prvé makroskopicky pomocí předpokládané hustoty (m)j S(r ) a za druhé mikroskopicky sečtením příspěvků všech molekulárních proudů Imol reprezentujících magnetické momenty molekul.
Pro první způsob výpočtu zavedeme jednotkový vektor N = n ℜ × t (srov. čl. 3.3.4). Hledaný proud pak lze vyjádřit ve tvaru [ (m)j S(r ).N ] Δ l. Za druhé předpokládejme, že na jednotkový objem tělesa připadá n0 molekul, z nichž každá je reprezentována smyčkou o magnetickém momentu m = ImolS mol. Ze zvětšené části smyčky na obrázku je zřejmé, že k celkovému proudu plochou obdélníčku budou přispívat jen smyčky vyplňující válcové těleso objemu Δ V, o kolmém průřezu t .S mol. (Smyčky, které jsou celé uvnitř obdélníčku, protínají jeho plochu dvakrát a k celkovému proudu nepřispívají.) Vezmeme-li v úvahu platnost vztahu M = n0m , dostaneme pro hledaný proud vyjádření Imoln0Δ l = -Imoln0(t .S mol)Δ l = -(M .t ) Δ l. Ze srovnání obou postupů plyne vztah
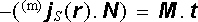 |
představující jen jiné vyjádření (3.115) .
Pro vyšetření poměrů uvnitř zmagnetovaného tělesa budeme počítat celkový magnetizační proud (m)I protékající plochou libovolně zvolené křivky l (viz obr. 3.28c). Lze opět postupovat dvěma způsoby; jednak makroskopicky pomocí předpokládané objemové hustoty (m)j magnetizačního proudu a jednak mikroskopicky sečtením příspěvků jednotlivých molekulárních proudů. V prvním případě lze magnetizační proud (m)I vyjádřit plošným integrálem typu (3.5) přes libovolnou plochu S ohraničenou křivkou l. Při použití druhého postupu si podle obr. 3.28c snadno uvědomíme, že nenulový příspěvek mohou dát jen smyčky, jejichž středy leží uvnitř čerchovaně vyznačeného prstencovitého tělesa. Jeho krátký úsek Δ l bude zřejmě přispívat hodnotou Δ (m)I = Imoln0Δ V = Imol(S mol.Δ l )n0 = M .Δ l . Integrací podél křivky l a využitím Stokesovy věty dostaneme ihned hledané vyjádření (3.116a) a (3.116) .
Z výsledků předchozího odstavce je patrné, že libovolné magnetické pole je možné popsat rovnicemi formulovanými v článku 3.3.2, jestliže kromě skutečných volných proudů budeme za zdroje tohoto pole považovat také vázané proudy reprezentující magnetizaci příslušných látek.
Kromě toho je zřejmé, že i v látkovém prostředí zůstane zachována uzavřenost magnetických indukčních čar. Tok vektoru magnetické indukce libovolnou uzavřenou plochou S bude vždy nulový, nezávisle na tom, leží-li tato plocha ve vakuu či v látkovém prostředí, viz (3.72) ,
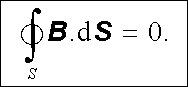 |
V libovolném bodě bude tedy platit, viz (3.73) ,
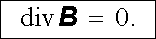 |
Pro libovolnou uzavřenou křivku l bude platit Amp`erův zákon (3.68) . Na pravé straně musí však vystupovat celkový volný I i vázaný (m)I proud protékající plochou křivky l
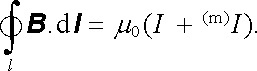 |
(3.134) |
Za vázaný proud je možné dosadit z rovnice (3.116a) . Dostaneme
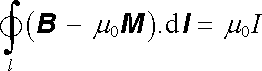 |
(3.135) |
nebo pomocí magnetické polarizace
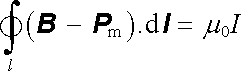 . . |
(3.135a) |
Poslední výraz lze zapsat ve velmi jednoduchém tvaru, ve kterém vystupují jen volné proudy, zavedeme-li novou veličinu
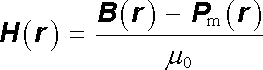 , , |
(3.136) |
nazývanou intenzita magnetického pole. Platí
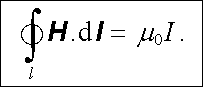 |
(3.137) |
Předpokládáme-li, že plochou ohraničenou křivkou l nepřetékají žádné plošné proudy, můžeme známým postupem využívajícím Stokesovu větu přejít k diferenciálnímu vyjádření vztahu (3.137)
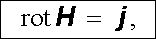 |
(3.138) |
v němž veličina
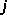 vyjadřuje hustotu volného objemového proudu v daném bodě.
vyjadřuje hustotu volného objemového proudu v daném bodě.
Výrazy (3.137) a (3.138) vyjadřují Amp`erův zákon pro magnetické pole v přítomnosti látkového prostředí. Pro doplnění jeho diferenciálního vyjádření (3.138) zbývá vyšetřit chování vektoru intenzity magnetického pole v okolí plošných proudů. Nechť danou libovolnou plochou S tečou volné i vázané plošné proudy o hustotách j S, (m)j S. Prostor nad plochou S nechť je vyplněn prostředím (1), jehož magnetická polarizace je P m1 a magnetická indukce je B 1. Podobně prostor pod ní nechť je vyplněn prostředím (2), o magnetické polarizaci P m2 (srov. obr. 3.17). Podle (3.84) bude při průchodu plochou S platit
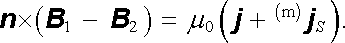 |
Po dosazení z (3.115) za (m)j S a po zavedení vektoru intenzity pole dostaneme konečnou podmínku
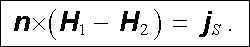 |
(3.139) |
Vidíme z ní, že nespojitost tečných složek vektoru intenzity magnetického pole je dána pouze hustotou volných plošných proudů. Při průchodu plochou, na níž jsou pouze vázané plošné proudy (například při průchodu povrchem zmagnetovaného tělesa), zůstávají tečné složky intenzity pole spojité.
Využitím Amp`erova zákona ve tvaru (3.137) je možné určit jednotku intenzity magnetického pole. V Mezinárodní soustavě pro ni dostaneme ampér na metr (A.m-1).
Intenzita magnetického pole byla zavedena formálně vztahem (3.136) . Vzniká proto otázka, jaký je její význam pro popis magnetického pole za přítomnosti látkového prostředí. Tento význam spočívá v platnosti výrazů (3.137) , (3.138) a (3.139) , které určují vztah vektoru intenzity magnetického pole k volnému proudu. Použití intenzity pole k popisu magnetického pole zmagnetovaných látek umožňuje vyloučit z explicitních úvah vázané proudy. Je ovšem samozřejmé, že pro bezprostřední vyjádření fyzikálních účinků magnetického pole (tj. pro vyjádření sil působících na pohybující se náboje - a jak uvidíme v kapitole 4 - také pro vyjádření jevu elektromagnetické indukce) zůstává i v látkovém prostředí určující veličinou vektor magnetické indukce.
Výrazy (3.137) , (3.138) , (3.139) a právě vyložený význam vektoru intenzity magnetického pole v mnohém připomínají situaci v oddílu 1.5, kde byla pro popis elektrostatického pole v dielektriku zavedena rovněž vektorová funkce - vektor elektrické indukce (srov. vztahy (1.247) , (1.248) , (1.252) ). Vlastnosti intenzity magnetického pole jsou skutečně v mnohém podobné vlastnostem vektoru elektrické indukce. Z praktického hlediska je však třeba považovat intenzitu magnetického pole za potřebnější veličinu než vektor elektrické indukce. Magnetické soustavy jsou totiž téměř vždy zadány rozložením volných proudů v prostoru. Je proto téměř vždy výhodné uvažovat veličinu, která má bezprostřednější vztah k těmto makroskopickým zdrojům. Užitečnost takového postupu bude demonstrována v následujících dvou článcích.
Při dosavadních úvahách o magnetickém poli za přítomnosti zmagnetovaných látek jsme považovali vektor magnetizace (respektive vektor magnetické polarizace) za známou funkci souřadnic a nestarali jsme se o to, jak souvisí jeho hodnota s fyzikálními podmínkami, ve kterých se látky nachází. Při řešení konkrétních úloh je ovšem znalost této souvislosti nezbytná. Je různá pro různé typy látek a je možné ji popsat pomocí fenomenologických materiálových veličin zavedených na základě výsledků experimentálního studia chování látek v magnetickém poli. (Srov. analogický postup v případě elektrostatického pole v čl. 1.5.4 či postup při formulaci Ohmova zákona ve stacionárním elektrickém poli v čl. 3.2.2.)
Uvedené relace mezi magnetickými veličinami, závislé na vlastnostech látek, se nazývají materiálovými vztahy. Na rozdíl od obecných rovnic formulovaných v článku 3.5.3, které popisují vlastnosti magnetického pole přesně, tj. v plné shodě s veškerou dosavadní experimentální zkušeností, vyjadřují dané konkrétní materiálové vztahy zpravidla jen přibližně chování skutečných látek. Pro různé účely je často třeba volit vztahy různého tvaru. V tomto článku se omezíme jen na zavedení lineárních materiálových relací v nejjednodušším tvaru, které relativně dobře vyhovují pro stacionární pole. Podrobnější diskusi chování látek v elektromagnetickém poli odkládáme do kapitoly 7.
Pro popis magnetických vlastností látek je nejdůležitější stanovit souvislost mezi magnetizací (popř. magnetickou polarizací) a magnetickým polem uvnitř látek. Vzhledem k tomu, že se vlastnosti látek zpravidla zkoumají ve vnějším poli vybuzeném proudem ve vodičích vhodného tvaru, je výhodné určovat souvislost mezi magnetizací a intenzitou pole uvnitř látky. Intenzita pole má totiž bezprostřednější vztah k volným proudům, jimiž je pole zadáno, než vektor magnetické indukce - viz článek 3.5.3.
Vyloučíme-li zatím z úvah látky v supravodivém stavu, o nichž bude jednáno v kapitole 7, je možné z hlediska chování v magnetickém poli rozdělit všechny látky do dvou velkých skupin. Do první skupiny zařazujeme látky, jejichž magnetizace nabývá jen malých hodnot. Mluvíme o látkách slabě magnetických. Do druhé skupiny zařazujeme naopak látky, jejichž magnetizace může nabývat značných hodnot. Jde o látky silně magnetické.
Pro slabě magnetické látky je až na výjimky charakteristická lineární závislost mezi intenzitou pole a magnetizací, která je velmi přesně splněna do značně vysokých polí (s výjimkou oboru velmi nízkých teplot). Je zvykem ji zapisovat ve tvaru
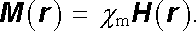 |
(3.140) |
Konstantu úměrnosti χ m nazýváme magnetickou susceptibilitou látky.[26] Pro magnetickou polarizaci dostaneme zřejmě podle (3.111)
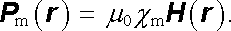 |
(3.141) |
Vzhledem k definičnímu vztahu pro intenzitu pole, můžeme snadno určit také vztah mezi magnetickou indukcí a intenzitou pole
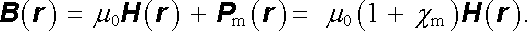 |
(3.142) |
Veličina = 0(1+χ m) se nazývá permeabilitou látky, veličina r = 1+χ m její relativní permeabilitou. Zatímco relativní permeabilita a magnetická susceptibilita jsou bezrozměrné veličiny, permeabilita má rozměr a jednotku shodnou s konstantou 0, a to (newton.ampér)-2. Ze vzorce (3.142) je také zřejmý původ názvu permeabilita vakua pro konstantu 0. Pro magnetické pole ve vakuu platí totiž = 0 takže
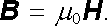 |
(3.143) |
Oba vektory se liší pouze konstantou; zavádění vektoru intenzity je tedy ve vakuu zbytečné.
Magnetická susceptibilita zavedená vztahem (3.140) je skalární veličina. Vektor magnetizace je v tomto případě vždy rovnoběžný s vektorem intenzity pole. To však platí jen v případě izotropních látek. V anizotropních látkách (např. v některých krystalech) je směr magnetizace obecně různý od směru intenzity pole. Magnetickou susceptibilitu je pak nutné považovat za symetrický tenzor druhého řádu (srov. vztahy (1.261) a (3.23) ). Pak platí
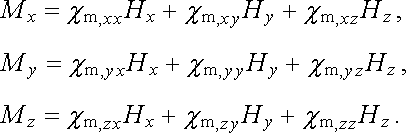 |
(3.140a) |
Magnetická susceptibilita může být kladná i záporná. Je-li záporná, mluvíme o látkách diamagnetických, látky s kladnou susceptibilitou nazýváme paramagnetickými. Diamagnetické jsou některé kovy, dále nekovové pevné látky, kapaliny a plyny (ale také například plazma) a většina látek organického původu. Paramagnetismus vykazuje většina kovů, některé soli v krystalickém stavu, vodné roztoky těchto solí, některé plyny (např. kyslík).
Magnetická susceptibilita diamagnetických látek téměř nezávisí na teplotě. Rovněž susceptibilita některých paramagnetických látek (zejména alkalických kovů) je teplotně nezávislá. U většiny paramagnetických látek se však susceptibilita s teplotou mění. Susceptibilita mnohých z nich splňuje tzv. Curieův zákon, který lze vyjádřit vztahem
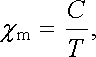 |
(3.144) |
v němž T je absolutní teplota a C tzv. Curieova konstanta, charakteristická pro danou látku. Absolutní hodnoty magnetické susceptibility slabě magnetických látek se za normálních podmínek zpravidla pohybují v intervalu 10-6 až 10-3.
Silně magnetické látky se od slabě magnetických neliší pouze velikostí magnetizace. Jejich dalším charakteristickým rysem je složitá závislost magnetizace na intenzitě pole, na historii vzorku, i na mnoha dalších faktorech.
Klasickými představiteli silně magnetických látek jsou látky feromagnetické. Při jejich cyklickém magnetování je závislost magnetizace na intenzitě pole dána tzv. hysterezní smyčkou. Na obrázku 3.29 jsou schematicky zobrazeny typické hysterezní smyčky feromagnetika odpovídající dvěma různým hodnotám maximálního pole Hm1 a Hm2[27] . Magnetizace vzorku, který byl ve výchozím stavu nezmagnetován, roste se vzrůstající intenzitou pole nejdříve podle křivky 0, Mm2, Mm1 nazývané křivkou prvotního magnetování. Maximálním hodnotám pole při daném cyklu Hm1, popř. Hm2, odpovídají maximální hodnoty magnetizace Mm1, popř. Mm2. Jak je z obrázku vidět, pro hodnoty pole menší než jistá hodnota HS magnetizace poměrně rychle vzrůstá. Při poli o hodnotě HS dosahuje vzorek magnetického nasycení a při jeho dalším zvyšování magnetizace vzrůstá již jen nepatrně. Hodnota magnetizace MS se nazývá spontánní magnetizací daného feromagnetika. Závisí na teplotě a představuje jednu z jeho základních charakteristik. Například pro čisté železo při pokojové teplotě je PmS = 0MS = 2,15Wb.m-2.
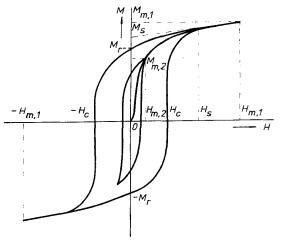
Obr. 3.29 Hysterezní smyčka feromagnetika.
Při následujícím snižování pole klesá magnetizace podle zcela jiné křivky. Například, byl-li vzorek magneticky nasycen, bude to křivka Mm1, Mr. Nenulová hodnota magnetizace Mr, odpovídající nulovému poli se nazývá remanentní magnetizací. Další snižování magnetizace může být dosaženo přiložením pole opačného směru. Hodnota intenzity Hc, při níž magnetizace klesne opět na nulu, se nazývá koercitivním polem. Při dalším zvyšování pole má magnetizace opačný směr a vzrůstá podle křivky -Hc, -Mm1 do své maximální hodnoty -Mm1 a při opětném snižování pole se proces opakuje podle křivky -Mm1, -Mr. Opakované cyklické změny intenzity pole s danými maximálními hodnotami vyvolávají cyklické změny magnetizace určené jednotlivými větvemi smyčky Mm1, -Hc, -Mm1, Hc; nulové hodnotě pole již neodpovídá nulová magnetizace. Kvalitativně podobný charakter má průběh magnetizace i v případě, kdy vzorek nedosahuje nasycení (viz obr. 3.29). Nezmagnetovaný stav, kdy nulovému poli odpovídá nulová magnetizace, může být opět dosažen cyklickým magnetováním s postupně klesající amplitudou pole k nule; amplituda magnetizace při jednotlivých cyklech pak klesá k nule podle křivky prvotního magnetování.
Pro feromagnetické látky lze zavést pojem permeability a relativní permeability r. Analogicky k (3.142) definujeme
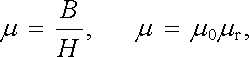 |
(3.145) |
přičemž požadujeme, aby magnetizace probíhala po křivce prvotního magnetování. Takto definovanou permeabilitu lze tedy změřit jedině na vzorku, který měl v nulovém stavu nulovou magnetizaci, tj. byl v nezmagnetovaném stavu. Relativní permeabilita feromagnetických látek má zpravidla hodnotu značně větší než jedna. Je samozřejmě závislá na intenzitě magnetického pole. Na obrázku 3.30 je uvedena typická závislost tohoto druhu pro ocel "Armco". Význačnými body na této křivce jsou počáteční permeabilita r,p, odpovídající malým hodnotám pole, a maximální permeabilita r,max.


Nejznámějšími představiteli látek jevících feromagnetismus za pokojové teploty jsou prvky železo, kobalt, nikl, gadolinium. Kromě gadolinia jeví feromagnetismus za nižších teplot také další vzácné zeminy. Dále se feromagnetismus projevuje u velkého množství slitin i sloučenin nekovového charakteru. Pro technické účely se připravují feromagnetické materiály z různých hledisek.
Za prvé mohou
feromagnetické látky zmagnetované do určitého stavu sloužit jako zdroje
magnetického pole, tj. jako trvalé magnety. Pro tento typ použití je žádoucí,
aby magnetický stav látky byl pokud možno stálý, tedy aby co nejméně závisel na
různých vnějších vlivech, speciálně na vnějších polích. Tento požadavek bude
zřejmě splněn, bude-li látka mít co největší hodnotu koercitivního pole. Feromagnetika s vysokou hodnotou koercitivního pole se nazývají magneticky tvrdá. V praxi se za magneticky tvrdé považují látky, pro něž je Hc
 103A.m-1.
Vysoké koercitivní pole však není jediný požadavek kladený na magneticky
tvrdé materiály. Pro konstrukci trvalých magnetů je také žádoucí co největší
hodnota remanentní magnetizace Mr. Kvalita magneticky tvrdého feromagnetika se proto nejčastěji
vyjadřuje velikostí součinu Hc Mr.
103A.m-1.
Vysoké koercitivní pole však není jediný požadavek kladený na magneticky
tvrdé materiály. Pro konstrukci trvalých magnetů je také žádoucí co největší
hodnota remanentní magnetizace Mr. Kvalita magneticky tvrdého feromagnetika se proto nejčastěji
vyjadřuje velikostí součinu Hc Mr.
Při použití v
elektrických strojích (generátorech, elektromotorech, transfor-mátorech) a
jiných zařízeních s proměnným magnetickým polem (viz oddíl 4.2) je naopak žádoucí
používat materiály s nízkým koercitivním polem a s vysokou hodnotou
permeability. V tomto případě mluvíme o magneticky
měkkých feromagnetikách. Za magneticky měkká se v praxi považují
feromagnetika, pro než platí Hc
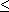 100A.m-1.
Zmíněná ocel "Armco" má Hc ℜ ≈
50A.m-1;
je klasickým magneticky měkkým feromagnetikem.
100A.m-1.
Zmíněná ocel "Armco" má Hc ℜ ≈
50A.m-1;
je klasickým magneticky měkkým feromagnetikem.
Jak již bylo
řečeno, spontánní magnetizace feromagnetika závisí na teplotě. S rostoucí
teplotou klesá, až při jisté kritické teplotě
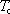 ,
nazývané Curieovou teplotou, klesne
na nulu. Nad Curieovou teplotou se látka zpravidla chová jako paramagnetikum.
,
nazývané Curieovou teplotou, klesne
na nulu. Nad Curieovou teplotou se látka zpravidla chová jako paramagnetikum.
Silný magnetismus látek může mít i jinou fyzikální podstatu než feromag-netismus.[28] Například technicky důležité magnetické materiály, nazývané ferity, jsou ferimagnetika. Bez ohledu na konkrétní podstatu silného magnetismu je pro tyto látky vždy charakteristické nelineární chování a hystereze. Pro přesný popis magnetického pole v takových látkách je tudíž vždy nutné znát příslušnou magnetizační křivku či smyčku. Pro méně přesné účely a pro mnohé obecné úvahy není třeba brát v úvahu detaily materiálových vztahů. Zavádějí se proto dva abstraktní typy magnetických látek, vystihující extrémní vlastnosti. Za prvé je to pojem ideálně magneticky měkkého prostředí, o němž se předpokládá, že je izotropní a splňuje přesně vztah (3.140) , respektive (3.142) . Za normálních podmínek vyhovují těmto předpokladům vlastně všechna magneticky izotropní diamagnetika a paramagnetika. Z magneticky silných materiálů je možné uvedený pojem přibližně použít pro magneticky měkké látky, přičemž se jejich vlastnosti podle situace popisují buď počáteční, nebo maximální permeabilitou (susceptibilitou).
Za druhé se zavádí pojem ideálně tvrdého magnetika, u něhož předpokládáme určitou hodnotu permanentní magnetizace, jež již nemůže být ovlivněna působením vnějšího magnetického pole. Je zřejmé, že tento pojem přibližně vystihuje například vlastnosti magneticky tvrdých feromagnetik. Za jejich permanentní magnetizaci je obvykle možné položit remanentní magnetizaci.
Problém výpočtu magnetického pole v látkách je jednoduchý v případě, kdy je celý prostor v němž pole uvažujeme, vyplněn homogenním, izotropním a lineárním prostředím. Pro vztah mezi magnetickou indukcí a intenzitou pole pak platí (3.142) , přičemž permeabilita je konstanta nezávislá na prostorových souřadnicích. Amp`erův zákon (3.137) lze užitím (3.142) vyjádřit pomocí magnetické indukce ve tvaru
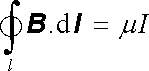 , , |
(3.146) |
zcela analogickém s (3.68) , který platí pro magnetické pole makroskopických proudů ve vakuu. Z této shody je patrné, že za uvedené situace můžeme použít všechny postupy formulované v článku 3.3.5. Je možné počítat přímo magnetickou indukci tak, že v příslušných vzorcích z článku 3.3.5 nahradíme permeabilitu vakua μ 0 permeabilitou daného materiálu .
Nejsou-li uvedené předpoklady splněny, je při výpočtu pole nutné vyjít z obecných rovnic formulovaných v článku 3.5.3. Speciálně při vyšetřování pole na plošném rozhraní dvou různých homogenních materiálů je nutné použít vztahů (3.72) a (3.139) . Z (3.72) vyplývá, že při průchodu rozhraním jsou spojité normálové složky vektoru magnetické indukce a z (3.139) plyne naopak spojitost tečných složek intenzity pole (neboť na vyšetřovaném rozhraní jsou volné plošné proudy nulové).
Velmi užitečnou pomůckou při řešení magnetických soustav v látkovém prostředí je pojem magnetického obvodu. Tento pojem vychází z toho, že magnetické indukční čáry jsou uzavřené křivky, podobně jako proudové čáry stacionárního proudu. Analogicky k proudovým trubicím stacionárního proudu je možné zavést pojem magnetické tokové trubice, která je rovněž uzavřená a vymezuje určitý konstantní magnetický tok. Na základě uvedené analogie je možné vyšetřovat magnetický tok tekoucí danou trubicí metodami stejnými, které byly v článcích 3.2.3 a 3.2.4 použity k vyšetřování stacionárního elektrického obvodu. Vznikne tak možnost formulovat vztahy zcela analogické s Ohmovým zákonem a Kirchhoffovými pravidly, pomocí nichž lze za určitých předpokladů počítat magnetické pole jednodušších soustav metodami vypracovanými pro elektrické obvody.
Magnetickým obvodem tedy rozumíme část prostoru vymezenou magnetickou tokovou trubicí, v níž se uzavírá určitý magnetický tok, buzený zpravidla elektrickým proudem protékajícím v okolních vodičích. Technický význam mají zejména obvody, jejichž podstatná část je tvořena materiály s vysokou magne-tickou permeabilitou. Příslušná toková trubice je pak vymezena povrchovými plochami součástí zhotovených z těchto materiálů.
Abychom mohli formulovat zákonitosti pro magnetický obvod, budeme uvažovat uzavřenou trubici magnetického toku Φ podle obr. 3.31. Trubice nechť prochází několika homogenními izotropními prostředími o permeabilitách 1, 2,..., >N. Uvnitř této trubice zvolme jistou indukční čáru l, jejíž úseky v jednotlivých prostředích označme l1, l2,..., lN. Konečně předpokládejme, že trubice je dostatečně úzká, aby magnetické pole uvnitř ní bylo možné považovat za homogenní. Magnetický tok bude potom možné vyjádřit ve tvaru Φ = BS, kde S je libovolný průřez trubice kolmý k indukční čáře l.
Nechť křivka l obepíná celkový proud Ic. Pro intenzitu pole H bude potom platit
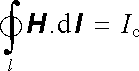 . . |
Veličina
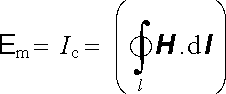 |
(3.147) |
představuje míru, kterou se na vytvoření magnetického pole v obvodu podílí vnější makroskopický proud. Nazývá se magnetomotorickým napětím působícím v obvodu.

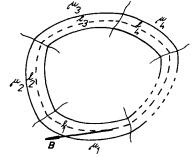
Magnetický tok je podél celého obvodu konstantní. Pro libovolný úsek li proto platí
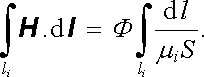 |
(3.148) |
V analogii s elektrickým obvodem je možné zavést veličinu
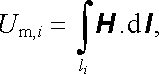 |
(3.149) |
kterou nazveme magnetickým napětím (spádem magnetického potenciálu) na úseku obvodu li. Dále můžeme srovnat křivkový integrál
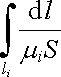 |
(3.150) |
s výrazem (3.20a) vyjadřujícím elektrický odpor určité části proudové trubice. Vzhledem k formální shodnosti obou výrazů můžeme zmíněný křivkový integrál (3.150) považovat za magnetický odpor příslušné části magnetického obvodu. (Permeabilita bude mít pak zřejmě význam měrné magnetické vodivosti.) Označíme-li jej Rm můžeme místo (3.148) psát
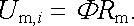 |
(3.151) |
Jestliže přirovnáme magnetický tok k elektrickému proudu, můžeme vztah (3.151) považovat za obdobu Ohmova zákona. Vyjadřuje skutečnost, že spád magnetického potenciálu je roven součinu magnetického toku a magnetického odporu, a bývá někdy nazýván Hopkinsonovým zákonem.
Pro celý obvod podle obr. 3.31 bude zřejmě platit
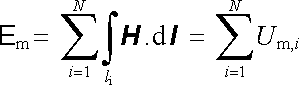 |
(3.152) |
a z druhé strany
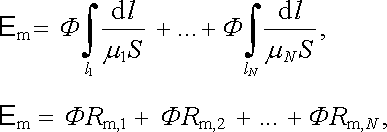 |
(3.153) |
čímž jsme opět dostali vztah zcela analogický s rovnicí (3.37) pro elektrický obvod.
Jednotkou magnetomotorického napětí i magnetického napětí je v soustavě jednotek SI zřejmě ampér. Vzhledem k tomu, že proud Ic v (3.147) představuje celkový proud protékající plochou křivky l, užívá se pro magnetomotorické napětí někdy také jednotka ampérzávit. Tento název vystihuje v praxi častou situaci, kdy je magnetické pole vytvářeno cívkou o z závitech protékanou proudem I. Pro celkový proud pak platí Ic = Iz.
V hledání analogií mezi elektrickým a magnetickým obvodem by bylo možné pokračovat například tím, že bychom uvažovali libovolně složitý rozvětvený obvod. Vzhledem k tomu, že výchozí vztahy (3.151) a (3.153) jsou totožné s odpovídajícími vztahy pro elektrický obvod, dále díky rovnici (3.72) , jíž je možné považovat za analogii rovnice kontinuity proudu, bychom jistě i v tomto případě dostali výsledky shodné s elektrickým obvodem. Speciálně bychom mohli formulovat Kirchhoffova pravidla pro magnetický obvod. Vzhledem k tomu, že analogie mezi oběma typy obvodů je dostatečně průhledná, nebudeme se již podrobným rozvíjením těchto úvah zabývat. V dalším výkladu ale budeme demonstrovat použití právě vyložených postupů na řešení několika příkladů.
V článku 3.5.3 jsme vyřešili otázku, jak mohou zmagnetovaná tělesa přispívat spolu s makroskopickými proudy k vytváření magnetického pole. V článku 3.5.4 bylo dále při vyšetřování vlastností feromagnetik poukázáno na možnost existence nenulové magnetizace i bez přítomnosti vnějšího pole. Uvedená vlastnost feromagnetik vytváří jednu z konkrétních možností existence magnetického pole vytvářeného pouze zmagnetovanými látkami, o níž byla zmínka v úvodu tohoto oddílu.
Magnetické pole, které vzniká bez přítomnosti volného makroskopického proudu a je pouze důsledkem nenulové magnetizace látek, se nazývá polem magnetostatickým. Jeho vlastnosti jsou plně popsány obecnými rovnicemi uvedenými v čl. 3.5.3, neboť jde o speciální případ magnetického pole v látkovém prostředí. Libovolná úloha o magnetostatickém poli může být vyřešena pomocí těchto rovnic; stačí znát magnetické vlastnosti a prostorové rozložení příslušných látek. V tomto článku se proto omezíme pouze na zdůraznění některých speciálních vlastností.
Ze vztahu (3.137) plyne pro libovolnou uzavřenou křivku
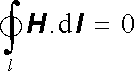 . . |
(3.154) |
Podobně z (3.138) dostáváme pro libovolný bod
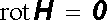 . . |
(3.155) |
Magnetostatické pole, které je polem objemově rozložených magnetických dipólů, je tedy potenciální a může být popsáno skalárním potenciálem. (O této vlastnosti magnetického pole objemově rozložených dipólů jsme se jiným způsobem přesvědčili již v článku 3.4.4.)
Ze známého průběhu magnetizace zmagnetovaných těles lze určit objemovou ρ m(r ℜ' ) a plošnou σ m(r ℜ' ) hustotu magnetických nábojů, a to ze vztahu, viz (3.118) ,
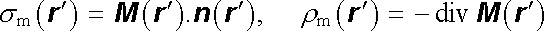 |
a magnetický potenciál může být vyjádřen vztahem (srov. (3.119) )
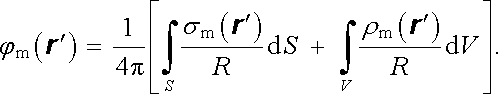 |
(3.156) |
Intenzita magnetostatického pole je pak dána zřejmým vztahem
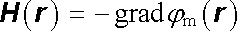 |
(3.157) |
a magnetická indukce podle (3.136) vztahem
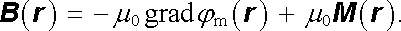 |
(3.158) |
Pro magnetostatické pole zůstávají samozřejmě v platnosti beze změny vztahy (3.72) , respektive (3.73) , neboť v nich volné proudy explicitně nevystupují. Dostáváme tedy soustavu rovnic, která je zcela totožná s rovnicemi elektrostatického pole za předpokladu nepřítomnosti volných nábojů (viz (1.253) ). (Takové elektrostatické pole je tvořeno pouze vázanými náboji na zpolarizovaných tělesech.) Na magnetostatické pole se tedy můžeme dívat jako na analogii pole elektrostatického.
Ze srovnání analogických rovnic vychází jako analogické veličiny intenzity pole E a H a podobnou analogii je možné vidět také mezi vektory elektrické a magnetické indukce D a B . Je však třeba si uvědomit, že tato analogie je pouze formální. Fyzikální účinky magnetického pole jsou bezprostředně popsány vektorem magnetické indukce B podobně, jako jsou fyzikální účinky elektrostatického pole bezprostředně popsány vektorem intenzity pole E . Proto, chceme-li hledat analogii mezi oběma typy polí, je nutné vidět fyzikálně opodstatněnější analogii mezi veličinami E a B . Úlohou zbylých veličin D a H je doplnit popis příslušných polí v látkovém prostředí. Charakteristickým znakem obou těchto vektorů je přitom jejich bezprostřednější vztah k makroskopickým zdrojům příslušných polí (k volným nábojům a k volným proudům). Konkrétní příklad řešení magnetostatického problému je uveden v 3.5.7b.
Uvažujme plošné rozhraní dvou homogenních izotropních prostředí o permeabilitách 1 a 2. Označme ϑ 1 úhel, který svírá magnetické pole v prvním prostředí s normálou rozhraní, a ϑ 2 analogický úhel pro magnetické pole ve druhém prostředí. Snadno nalezneme vztah mezi úhly ϑ 1, ϑ 2 a hodnotami permeabilit 1, 2. Jelikož je na rozhraní nulová hustota volného plošného proudu, plyne z (3.139) spojitost tečných složek intenzity magnetického pole H1sin ϑ 1 = H 2 sin ϑ 2 . Z (3.72) dostaneme postupem stejným jako v článku (1.5.6) spojitost normálových složek vektoru magnetické indukce. Tedy B1cosϑ 1 = B2cosϑ 2. Použitím (3.142) obdr-žíme z těchto podmínek výsledek
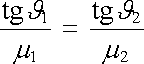 |
(3.159) |
shodný s analogickým vztahem (1.278) pro elektrostatické pole.
Speciálně, je-li první prostředí vzduch a druhé prostředí má vysokou hodnotu permeability, platí 1 = 0, 2 >> 0. Odtud získáme
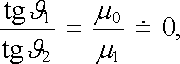 |
(3.160) |
což je možné jen v případě, že ϑ 1 B 0. Z prostředí o vysoké permeabilitě vy-stupuje tedy magnetické pole kolmo na jeho povrch.
Jako příklad na použití vlastností magnetického obvodu vypočítáme magnetické pole toroidní soustavy podle obr. 3.32. Nechť jádro zhotovené z materiálu o vysoké relativní permeabilitě r >> 1 ve tvaru prstence o středním poměru r0 se vzduchovou mezerou δ je ovinuto cívkou o z závitech. Vypočítáme magnetické pole v jádru i v mezeře za předpokladu, že cívkou teče proud I.


Budeme předpokládat, že průřez jádra je S. Dále budeme předpokládat, že šířka mezery je malá, takže magnetický tok Φ teče plochou S i v této mezeře. Pro magnetické odpory mezery i jádra potom dostaneme
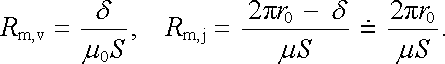 |
Po dosazení do (3.153) můžeme vypočítat magnetický tok tekoucí obvodem
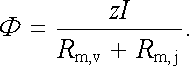 |
(3.161) |
Zavedeme označení Bj, Hj pro magnetickou indukci a intenzitu pole v jádru a podobně Bv, Hv pro tyto veličiny v mezeře. Bude pak platit
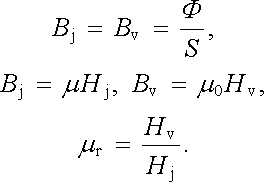 |
(3.162) |
Vidíme, že zatímco magnetická indukce má stejnou hodnotu ve vzduchu i v jádru, intenzita pole ve vzduchu je r-krát větší.
Právě vyřešený příklad ilustruje, proč je výhodné užívat při konstrukci magnetických soustav materiálů s vysokou permeabilitou. Jejich užitím se sníží magnetický odpor obvodu, čímž v příslušném poměru vzroste magnetický tok.
Ve stejném uspořádání si nyní ukážeme způsob řešení magnetostatického problému. Předpokládejme, že v cívce z obr. 3.32 byl vypnut proud, přičemž ve feromagnetickém jádru zůstala nenulová magnetizace konstantní hodnoty M0, (Pm,0 = 0M0), jejíž směr je v každém bodě rovnoběžný se směrem tečny kružnice o středu ležícím na ose prstence. Při použití označení zavedeného v čl. 3.5.5 bude platit
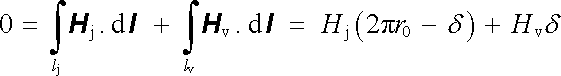 |
a dále vzhledem ke kolmosti vektorů B j, B v k povrchu jádra
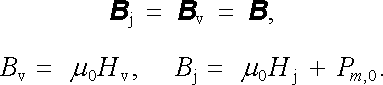 |
Odtud dostaneme jednoduchým výpočtem
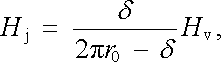 |
(3.163) |
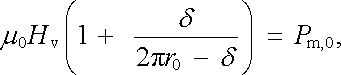 |
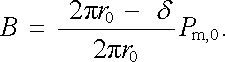 |
(3.164) |

Ze získaných výsledků je patrné, že intenzita pole Hj uvnitř jádra má opačný směr než vektor magnetické indukce a než intenzita pole ve vzduchové mezeře. To je dáno tím, že celou její hodnotu určuje demagnetizační pole. Z (3.164) pro ni dostaneme
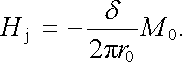 |
(3.165) |
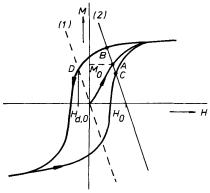
Velikost magnetické indukce B i intenzity pole uvnitř jádra Hj je úměrná magnetizaci jádra M0. Hodnotu Hj lze odečíst z hysterezní smyčky. Je dána průsečíkem demagnetizační přímky (3.165) s klesající větví hysterezní smyčky (průsečík analogický bodu D na obr. 3.33).
Rozložení magnetického pole vytvořeného magneticky homogenní a izotropní koulí vloženou do vnějšího magnetického pole je možné počítat způsobem zcela analogickým s tím, který byl použit při výpočtu elektrostatického pole dielektrické koule (viz příklad 1.5.6c). Ze stejných důvodů především platí, že homogenní těleso tvaru koule (nebo obecněji elipsoidu), vložené do vnějšího homogenního magnetického pole B 0, bude homogenně zmagnetováno. Označíme-li tuto jeho magnetizaci M 0, bude výsledný magnetický dipólový moment tělesa roven
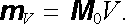 |
(3.166) |
Výsledné magnetické pole vně koule bude superpozicí vnějšího pole B 0 a pole B m vytvořeného v daném bodě zmagnetovanou koulí. Podle výsledků příkladů 3.4.4 a 1.5.6c je zřejmé, že vně koule bude pole B m totožné s polem magnetického dipólu o magnetickém momentu m V umístěného ve středu koule.
Stejným postupem jako v 1.5.6c pro pole elektrostatické bychom zjistili, že uvnitř koule se vlivem jejího zmagnetování vytvoří homogenní demagnetizační pole o intenzitě H d, které se vektorově sečte s původním vnějším polem B 0. Analogicky k (1.184) platí
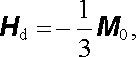 |
(3.167) |
a pro výsledné pole uvnitř koule dostaneme
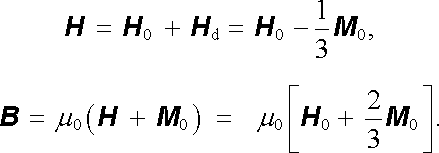 |
(3.168) |
V případě, že materiál koule může být považován za lineární měkké magnetikum, může být magnetizace vyjádřena pomocí magnetické susceptibility; M 0 = χ mH a pro výsledné pole dostaneme výrazy
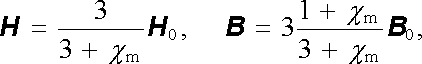 |
(3.169) |
které jsou analogické k (1.281) , popř. (1.282) .
V případě, že materiál koule je feromagnetikum, je situace složitější, neboť vztah mezi magnetizaci a výsledným polem uvnitř koule je dán hysterezní smyčkou. Skutečná magnetizace materiálu koule M 0 i výsledné magnetické pole uvnitř může být určeno z hysterezní smyčky způsobem uvedeným v obr. 3.33. Závislost demagnetizačního pole H d na magnetizaci, daná vztahem (3.167a) , může být v obrázku znázorněna přímkou (l) a podobně závislost výsledného pole H na magnetizaci přímkou (2). Průsečíky A, B, C této přímky s hysterezní smyčkou udávají možné hodnoty magnetizace materiálu. O tom, která z nich se bude skutečně realizovat, rozhodne postup, jakým bylo vnější pole nastaveno. Například při jeho monotónním zvyšování z nuly na konečnou hodnotu H0 za předpokladu, že materiál byl původně v nezmagnetovaném stavu, nastane případ A. Z křivky prvotní magnetizace lze pro danou hodnotu magnetizace M0 odečíst i příslušnou hodnotu výsledného pole H.
Výsledky získané v předchozím příkladu pro těleso tvaru koule snadno zobecníme pro obecný elipsoid za předpokladu, že vnější pole je orientováno ve směru jedné z jeho hlavních os. Využijeme k tomu opět analogii mezi elektrostatickým a magnetickým polem prostorově rozložených dipólů (srov. čl. 1.3.4 a 3.4.4).
Podobně jako v elektrostatickém poli (viz 1.5.6c) platí, že magneticky homogenní těleso tvaru elipsoidu je ve vnějším homogenním magnetickém poli H 0 homogenně zmagnetováno. Pro jeho výsledný magnetický dipólový moment platí opět vztah (3.166) .
Za předpokladu, že vnější pole H 0 je orientováno ve směru jedné z hlavních os elipsoidu, má homogenní demagnetizační pole H d uvnitř elipsoidu rovněž směr této osy a platí
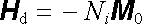 , , |
(3.167a) |
kde Ni je hlavní hodnota demagnetizačního (depolarizačního) faktoru příslušející dané hlavní ose elipsoidu[29] . Výsledné magnetické pole uvnitř elipsoidu je pak místo (3.168) dáno vztahem
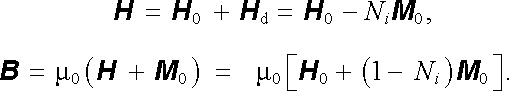 |
(3.168a) |
Pro lineární magneticky měkké magnetikum pak platí
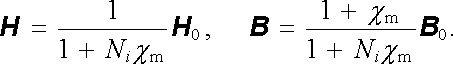 |
(3.169a) |
V případě feromagnetického tělesa lze opět postupovat podle obr. 3.33 s tím, že demagnetizační přímky mají směrnici danou demagnetizačním faktorem.
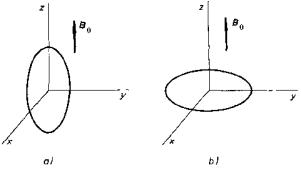
Obr. 3.34 K výkladu demagnetizačních polí v rotačním elipsoidu magnetovaném ve směru rotační osy z: a) protáhlý elipsoid, b) zploštělý elipsoid. V daném označení os platí pro hlavní hodnoty demagnetizačního faktoru N1 = Nx, N2 = Ny, N3 = Nz.
Výsledky (3.167) až (3.169) pro kouli dostaneme jako speciální případ z (3.167a) až (3.169a) , uvědomíme-li si, že pro kouli platí N1 = N2 = N3 = 1/3. Důležité jsou rovněž dva další speciální případy: velmi protáhlý rotační elipsoid magnetovaný podél osy rotační symetrie (obr. 3.34a) a zploštělý rotační elipsoid magnetovaný rovněž podél své rotační osy (obr. 3.34b). V prvním případě můžeme zřejmě přibližně položit Nx = Ny B 1/2, Nz B 0. Demagnetizační pole je tedy podle (3.167a) přibližně nulové a intenzita pole uvnitř elipsoidu je přibližně rovna H 0 . Ve druhém případě platí naopak Nx = Ny B 0, Nz B 1 a pro demagnetizační pole platí
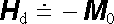 . . |
(3.167b) |
Výsledné pole uvnitř elipsoidu je podle (3.168a) v prvním případě rovno
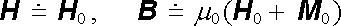 |
(3.168b) |
a v druhém případě platí
 . . |
(3.168c) |
ÚLOHY KE KAPITOLE 3
Ú 3.1: Uvnitř homogenního izotropního tělesa s měrnou vodivostí γ nechť v okamžiku t = 0 existuje volný náboj charakterizovaný objemovou hustotou ρ 0. Jak se bude tento náboj měnit s časem? Odhadněte konkrétní hodnoty pro měď (γ = 0,6.108 >-1.m-1), polovodič o měrné vodivosti γ = 100 >-1.m-1 a izolant (sklo) o měrné vodivosti γ = 10-12 >-1.m-1.. Relativní permitivitu položte rovnu jedné.
Ú 3.2: Určete:
a) vstupní odpor, tj. odpor RAB mezi body A, B, nekonečného řetězce složeného z odporů R1, R2 podle obr. 3.35.
b) odpor RAB mezi body A, B sítě podle obr. 1.66, v níž jsou všechny kapacity nahrazeny odpory R. Výsledek srovnejte s výsledkem úlohy Ú 1.30.
c) odpor mezi protilehlými vrcholy krychle, jejíž každá hrana reprezentuje odpor R.

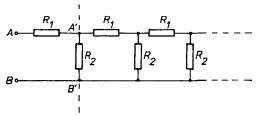
Ú 3.3: Určete změnu Δ R paralelního spojení odporů R1, R2 způsobenou změnou odporu R2 o Δ R2.
Ú 3.4: Jakou změnu odporu můžeme očekávat, když napneme měděný drát tak, že se prodlouží o 0,1 %?
Ú 3.5: Z desky tloušťky t zhotovené z materiálu o měrné vodivosti γ je vyříznuto mezikruží o vnitřním poloměru r1 a vnějším r2. Stanovte odpor R mezikruží, slouží-li jako přívody proudu obě válcové plochy, kterými je omezeno. Předpokládejte, že vodivost přívodů je nekonečně velká a tloušťka desky malá ve srovnání s oběma poloměry.
Ú 3.6: Za jak dlouho ohřeje ponorný vařič 2 litry vody z 20 °C na 90 °C? Vařič je připojen na síť o napětí U = 220 V, jeho odpor je R = 100 činnost je 75 %. (Změnu odporu vařiče s teplotou zanedbejte).
Ú 3.7: Ke zdroji o elektromotorickém napětí E = 100 V a vnitřním odporu Ri = 5 Ω je připojena paralelní kombinace proměnného odporu R a pevného odporu R' = 10 lezněte hodnotu odporu R, do něhož zdroj dodá výkon 100 W.
Ú 3.8: Dva kruhové závity o stejném poloměru R0 jsou umístěny souose ve vzájemné vzdálenosti l tak, že jejich roviny jsou kolmé ke společné ose. Oběma závity protéká proud I0 stejném směru. Odvoďte výraz pro magnetickou indukci B na ose obou závitů. Vypočítejte hodnotu magnetické indukce Bz ve středu závitu a magnetickou indukci BH uprostřed na ose mezi závity v případě R0 = 10 cm, l = 20 cm, I0 = 3 A.
Ú 3.9: Pro dvojici závitů z předchozí úlohy Ú 3.8 nalezněte relaci mezi poloměrem R0 a vzdáleností l, při níž má pole BH maximální homogenitu ve směru spojnice středů obou závitů.
Ú 3.10: Jaký vztah musí platit mezi délkou l a průměrem D solenoidu, aby bylo možné počítat pole v jeho středu podle vzorce pro nekonečný solenoid s chybou nepřesahující l %?
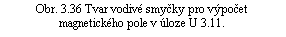

Ú 3.11: Nekonečný drát je ohnut do půlkruhu poloměru r, jak je naznačeno na obr. 3.36. Určete magnetickou indukci B ve středu půlkruhu za předpokladu, že drátem protéká proud I.
Ú 3.12: Určete magnetickou indukci B ve středu smyčky ve tvaru:
a) kružnice o poloměru r,
b) rovnostranného trojúhelníka o straně a,
c) čtverce o straně a,
d) obdélníka o stranách a, b,
e) pravidelného šestiúhelníka o straně a.
Ú 3.13: Čtvercovou smyčkou o straně 6 m protéká proud 10 A. Určete magnetickou indukci B v bodě na ose smyčky ve výšce 4 m nad rovinou smyčky.
Ú 3.14: Uvnitř dlouhého přímého homogenního vodiče kruhového průřezu je vyvrtána podélná válcová dutina, jejíž osa je rovnoběžná s osou vodiče. Vzájemná vzdálenost obou os je a a vodičem protéká proud o hustotě j. Jakou velikost má magnetická indukce v dutině?
Ú 3.15: Vypočtěte magnetický tok Φ plochou čtverce o straně a = 3 cm umístěného vedle nekonečně dlouhého přímého drátu, jímž protéká proud I = 15 A. Jedna strana čtverce je rovnoběžná s drátem ve vzdálenosti 4 cm, protilehlá strana je od drátu vzdálena 5 cm.
Ú 3.16: Nalezněte průběh hustoty plošného proudu jS tekoucího na povrchu koule poloměru r0, který uvnitř koule vytvoří homogenní pole B 0. Ukažte, že vně koule je toto pole ekvivalentní poli dipólu a určete jeho dipólový moment m .
Ú 3.17: Magnetický dipól o magnetickém momentu m je umístěn v homogenním magnetickém poli B 0, přičemž vektory B 0 a m jsou orientovány antiparalelně. Nalezněte poloměr koule r0, jejímž povrchem neprochází žádné magnetické indukční čáry výsledného pole. Určete výslednou magnetickou indukci Br na "rovníkové" kružnici této koule.
Ú 3.18: Válcová tyč poloměru r0 a délky l z magnetického materiálu je cirkulárně zmagnetována tak, že čáry magnetizace M tvoří koaxiální kružnice, přičemž velikost magnetizace vzrůstá se vzdáleností od osy; M = kr, k je konstanta. Vyjádřete hustoty magnetizačních proudů (m)j, (m)jS, magnetickou indukci B a intenzitu pole H uvnitř tyče.
Ú 3.19: Určete intenzitu pole H a magnetizaci M uvnitř bizmutové koule vložené do vnějšího homogenního magnetického pole B0 = 1,0 T. Pro magnetickou susceptibilitu bizmutu použijte hodnotu uvedenou v tabulce 7.4.
Ú 3.20: Určete intenzitu pole H a magnetizaci M uvnitř koule z oceli "Armco" vložené do vnějšího magnetického pole B0 = 1,0 T. Výpočet proveďte za zjednodušujícího předpokladu, že relativní permeabilita materiálu nezávisí na magnetickém poli a je rovna počáteční permeabilitě r,p = 300 (srov. obr. 3.30).
[15] O orientaci plochy viz Dodatek l.
[16] Polarizační proud v dielektriku je jediným typem vázaných proudů, který reprezentuje makroskopické změny v rozložení skutečných nábojů. V oddílu 3.5 bude zaveden jiný typ vázaného proudu, tzv. magnetizační proud v magnetiku, pomocí něhož lze popsat vliv látkového prostředí na výsledné magnetické pole v daném místě. Magnetizační proud však nereprezentuje žádný přenos náboje v makroskopickém měřítku, a nevyjadřuje tudíž žádný skutečný makroskopický proud ve smyslu uvedené definice. Nebudeme jej proto v tomto článku uvažovat. Podobný charakter má i tzv. Maxwellův proud ve vakuu, který se zavádí při formulaci obecných rovnic nestacionárního elektromagnetického pole (viz kapitola 5).
[17] Vedle stacionárního elektrického pole budí pohybující se náboje ještě stacionární pole magnetické. Jeho vlastnosti budeme vyšetřovat v následujícím oddílu.
[18] Zavedení vektoru elektrické polarizace a elektrické indukce pro vodiče je zcela logické. V každém vodiči jsou totiž kromě volných nositelů náboje ještě další objekty složené z kladně a záporně nabitých částic (ionty, molekuly, krystalová mřížka v kovech apod.). O nich je třeba předpokládat, že se mohou polarizovat. Elektrické pole způsobí tedy nejen vznik elektrického proudu, ale obecně i vznik nenulové elektrické polarizace prostředí a s ní související vznik makroskopických vázaných nábojů. (V elektrostatice není nutné polarizaci vodičů uvažovat proto, že intenzita pole je v nich nulová). Experimentální studium polarizace vodičů je ovšem značně ztíženo přítomností volných nábojů, takže konkrétní hodnoty susceptibility či permitivity nejsou zpravidla známé.
[19] Význam makroskopického magnetického pole v látkovém prostředí je zcela analogický makroskopickému elektrostatickému poli v látkách, vyšetřovanému v oddílu 1.5. Vzájemnému vztahu makroskopického a mikro-skopického pole bude věnována pozornost ještě v kapitole 5.
[20] V článku 3.4.5 uvidíme, že v některých speciálních případech lze pojem "magnetického náboje" formálně zavést. Výhoda takového postupu spočívá v analogii s popisem elektrostatického pole.
[21] Ani kalibrační podmínka (3.76) spolu s definičním vztahem (3.74) však neurčují vektorový potenciál jednoznačně (srov. příklad 3.3.5e).
[22] Pro nestacionární elektromagnetické pole lze vektorový potenciál rovněž zavést. Je však pro něj nutné uvažovat jinou kalibrační podmínku (viz kapitolu 5).
[23] Postup výpočtu vektorového potenciálu nekonečně dlouhého solenoidu pomocí vztahu (3.82) je dosti podrobně popsán například v knize W. T. Scott: The Physics of Electricity and Magnetism, J. Wiley, New York 1966.
[24] Vedle Amp`erova magnetického momentu se v soustavě jednotek SI zavádí Coulombův magnetický moment p m = 0m .
[25] Vedle magnetizace se v Mezinárodní soustavě jednotek zavádí vektor magnetické polarizace P m ( r ), který představuje objemovou hustotu Coulombova magnetického momentu. Platí tedy
P m(r ) = 0M (r ). (3.111)
[26] Vedle susceptibility χ m se někdy užívá též tzv. měrná susceptibilita κ m = χ m/ρ M, kde ρ M je hustota daného materiálu. Měrná susceptibilita vyjadřuje vztahem analogickým k (3.140) magnetický moment vztažený na jednotkovou hmotnost. Má význam například u práškových materiálů, kdy je obtížné určit skutečný objem vyšetřované látky.
[27] Hysterezní křivka feromagnetika má kvalitativně stejný průběh jako hysterezní křivka feroelektrika, o kterém pojednáme v kapitole 7 (srov. článek 7.2.1).
[28] Fyzikální podstatou silného magnetismu je tzv. spontánní uspořádání magnetických momentů atomů. Podle geometrie uspořádání rozeznáváme feromagnetika, ferimagnetika, antiferomagnetika a jiné. Silná magnetika mají takový typ magnetického uspořádání, u něhož se magnetické momenty atomů vzájemně nevykompenzují (feromagnetika, ferimagnetika). Typ magnetického uspořádání, u něhož jsou tyto momenty navzájem vykompenzovány, vede naopak na slabý magnetismus (například antiferomagnetika). Podrobněji o těchto otázkách pojednáme v kapitole 7.
[29] Depolarizační faktor je obecně tenzorová veličina. Součet jeho hlavních hodnot je roven jedné N1 + N2 + N3 = 1 (viz například [7]).