 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Již ve starověku bylo známé silové působení mezi určitými (zmagnetovanými) látkami. Z látek jevících takové chování byly známy některé nerosty obsahující především oxidy železa (magnetit Fe3O4, maghemit γ -Fe2O3 apod.) a také kovové železo. Byla také známa existence zemského magnetismu a magnetka.
Nová etapa ve vývoji poznatků o magnetismu nastala objevem magnetických účinků vodičů protékaných proudem. Byly to především experimenty H. Ch. Oersteda, který (r. 1820) objevil silové působení mezi vodičem protékaným proudem a magnetkou. Zjistil, že magnetka umístěná do blízkosti vodiče protékaného proudem se vychýlí ze svého původního směru určeného zemským magnetismem. V případě dlouhého přímého vodiče má magnetka tendenci zaujímat polohu kolmou k vodiči, přičemž její orientace závisí na směru proudu. Záhy po Oerstedových objevech objevil A. M. Amp`ere silové působení mezi dvěma vodiči protékanými proudem. Známá je především Amp`erova modifikace Oerstedova pokusu, ve kterém byla magnetka nahrazena válcovou cívečkou protékanou proudem a bylo zjištěno, že chování cívečky je zcela analogické chování magnetky. Jiným známým typem Amp`erova experimentu je silové působení mezi přímými vodiči protékanými proudem: Dva rovnoběžné vodiče se přitahují, teče-li v nich proud stejným směrem a naopak se odpuzují při opačných směrech proudu. Jsou-li dva přímé a dostatečně dlouhé vodiče navzájem kolmé, téměř na sebe nepůsobí.
Na základě poznatků získaných z experimentů popsaného typu byl zaveden pojem magnetického pole, které se projevuje silovými účinky na zmagnetovaná tělesa, vodiče protékané proudem, či na pohybující se nositele elektrického náboje. Zdrojem magnetického pole mohou být zmagnetovaná tělesa nebo makroskopické elektrické proudy. Velmi důležitou pro teorii elektromagnetických jevů, která vznikala hlavně ve druhé polovině devatenáctého století, byla otázka, zda jsou jednotlivé mechanismy elektrického proudu (viz čl. 3.1.2) z hlediska magnetických účinků ekvivalentní. Tato otázka byla experimentálně studována řadou fyziků ještě na přelomu devatenáctého a dvacátého století. Známé jsou například experimenty H. Rowlanda (1876) a W. C. Roentgena (1888), které prokázaly magnetické účinky konvekčního proudu realizovaného makroskopickým pohybem těles nesoucích volné či vázané náboje. Těmito a dalšími podobnými experimenty byla jednoznačně prokázána ekvivalence magnetických účinků všech typů proudu. Objev speciální teorie relativity pak přinesl možnosti kvalitativně nového pohledu na podstatu magnetických účinků elektrického proudu. Jak bylo v kapitole 2 ukázáno jednoduchou aplikací Lorentzovy transformace, elektrické a magnetické pole představují jen dvě různé stránky vzájemné interakce pohybujících se nábojů. Zatímco elektrické pole (a jeho intenzita definovaná vztahy typu (1.32) , popř. (2.26) ), vyjadřuje tu část silových účinků mezi náboji, která je nezávislá na rychlosti "zkušebního" náboje vůči pozorovací soustavě souřadné, magnetické pole popisuje naopak část silových účinků na této rychlosti závislou.
V tomto oddílu se budeme podrobně zabývat vlastnostmi stacionárního magnetického pole. Budeme přitom přísně stát na stanovisku klasické fyziky. Existenci magnetického pole budeme považovat za nový fyzikální poznatek vyplývající z experimentů Oerstedova a Amp`erova typu.
Experimenty Oerstedova a Amp`erova typu ukazují, že magnetické pole může být v dané části prostoru vytvořeno buď náboji libovolného typu, pohybujícími se v makroskopickém měřítku, nebo přítomností látek nacházejících se ve zvláštním (zmagnetovaném) stavu. Experiment dále ukazuje , že makroskopické magnetické pole může existovat ve vakuu i v látkovém prostředí.[19] Magnetické pole se projevuje silovými účinky jednak na vodiče protékané makroskopickým proudem, jednak na pohybující se tělesa nesoucí libovolný náboj, ale má rovněž účinky na všechny druhy látek v klidu.
Uvedené silové účinky je výhodné popsat pomocí vektorového pole. Lze si představit, že příslušné vodiče či zmagnetovaná tělesa vytvářejí ve svém okolí magnetické pole, které působí na jiné vodiče či na jiná tělesa. Výhodnost takového postupu byla dostatečně prokázána v kapitole o elektrostatice (srov. čl. 1.2.1), takže se již nemusíme jeho zdůvodňováním zabývat.
Podrobný kvantitativní rozbor výsledků jednotlivých typů experimentů dovoluje formulovat základní definiční vztah pro veličinu charakterizující magnetické pole, která se z historických důvodů nazývá magnetickou indukcí. Uvažujme nejdříve částici malých rozměrů nesoucí náboj q, který budeme považovat za bodový náboj. Jestliže se tato částice bude pohybovat v blízkosti vodičů protékaných proudem či v blízkosti zmagnetovaných těles, lze ukázat (viz též oddíl 2.2), že celkovou sílu F působící na částici lze vyjádřit vztahem
 |
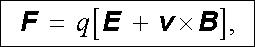(3.56) |
v němž v je rychlost částice v dané inerciální soustavě. Vzorec (3.56) se nazývá Lorentzovým vzorcem, je zobecněním vztahu (1.32) a může být považován za definiční vztah pro intenzitu elektrického pole E i pro magnetickou indukci B (srov. vztahy (2.41) a (2.58) ). V případě, že elektrické pole je v daném místě nulové, působí na částici jen magnetická síla, která je dána vztahem
 |
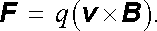(3.57) |
Další zobecnění vztahu (3.57) dostaneme, budeme-li místo jediného "zkušebního náboje" q uvažovat působení magnetického pole na libovolný proud popsaný hustotou proudu j (r ). V tomto případě je výhodné uvažovat sílu působící na nositele proudu v jednotkovém objemu vodiče, tedy objemovou hustotu síly f . Podle vztahů (3.8) až (3.11) je možné vyjádřit hustotu proudu pomocí hustoty nábojů ρ (podílejících se na vedení proudu) a pomocí jejich rychlosti. Pro hustotu síly f pak podle (3.57) zřejmě dostaneme
 |
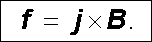(3.58) |
Výraz (3.58) platí nezávisle na tom, jakým mechanismem je proudová hustota realizována. Udává vztah mezi okamžitými hodnotami síly f , proudové hustoty j a magnetické indukce B v daném bodě. Fyzikální obsah vztahu (3.58) je zřejmě stejný jako fyzikální obsah vzorce (3.57) . Je tedy lhostejné, který z nich budeme za definici vektoru magnetické indukce považovat.
Jednotka magnetické indukce v Mezinárodní soustavě se nazývá tesla (T). Ze vztahu (3.57) , popř. (3.58) , snadno odvodíme, že tesla = newton.(amper.metr)-1. Lze tedy říci, že magnetické pole l tesla působí na náboj jednoho coulombu, který se pohybuje rychlostí jednoho metru za sekundu, silou jednoho newtonu (za předpokladu, že směr rychlosti náboje je kolmý ke směru pole).
Jako pro každé vektorové pole, lze také pro vektor magnetické indukce zavést pojem toku (srov. čl. 1.2.2). Mluvíme o magnetickém toku Φ . Pro libovolnou orientovanou plochu S platí
 |
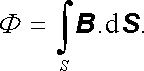(3.59) |
Jednotkou magnetického toku je jeden weber (Wb). Podle definiční relace jednotky magnetické indukce platí: weber = joule.sekunda.coulomb-1. V příští kapitole uvidíme, že také platí: weber = volt.sekunda.
V předchozím článku jsme se seznámili s fyzikálními účinky magnetického pole a zavedli jsme vektorovou veličinu B jako jeho kvantitativní míru. Vztahy, které jsme získali, platí obecně pro libovolné magnetické pole ve stacionárním přiblížení. Platí pro pole ve vakuu i v látkovém prostředí, nezávisle na tom, jakou měrou se na jeho vzniku podílejí makroskopické proudy ve vodičích, jiné mechanismy pohybu nábojů (konvekční proudy i pohyb nabitých makroskopických těles) a zmagnetovaná tělesa.
Dosud však nevíme, jaký je vztah daného magnetického pole k jeho zdrojům. To znamená, že neumíme určit vektor magnetické indukce v daném bodě, i když známe rozložení proudů ve vodičích i vlastnosti příslušného prostředí. Otázkami tohoto druhu se nyní budeme postupně zabývat. Nejdříve se zaměříme na magnetické pole ve vakuu vytvářené soustavou vodičů protékaných proudem.
Vyjdeme z experimentů o silovém působení magnetického pole a budeme nejdříve uvažovat pole přímého nekonečně dlouhého vodiče. Příslušné experimenty by ukázaly, že vektor magnetické indukce B má vždy směr tečny ke koncentrickým kružnicím se středy na ose vodiče, ležícími v rovině kolmé na směr vodiče. Velikost vektoru magnetické indukce ve vzdálenosti a od osy vodiče by byla přímo úměrná velikosti proudu I protékajícího vodičem a nepřímo úměrná vzdálenosti a. Bylo by tedy možné vyjádřit ji vztahem
 |
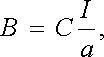(3.60) |
v němž C je konstanta související s volbou jednotky proudu.
Jestliže do magnetického pole vyšetřovaného vodiče vložíme jiný přímý nekonečně dlouhý vodič protékaný proudem Iℜ' , který je s prvním vodičem rovnoběžný, lze pomocí vzorce (3.58) vypočítat silové působení mezi oběma vodiči. Podle toho co bylo o orientaci vektoru magnetické indukce přímého vodiče řečeno je zřejmé, že vodiče v závislosti na vzájemné orientaci proudů I, popř. Iℜ' , se budou buď přitahovat, nebo odpuzovat. Ze vzorce (3.58) snadno určíme velikost příslušné síly (l)F působící na daný úsek vodiče o délce l. Platí
 |
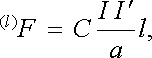(3.61) |
což je známý Amp`erův vzorec.
Vztahu (3.61) bylo jak známo použito k definici jednotky proudu (viz Dodatek 2). V Mezinárodní soustavě jednotek byla tato jednotka (jeden ampér) zvolena tak, že konstanta C v (3.60) , respektive (3.61) je z definice rovna C = 2.10-7 newton.ampér-2. Vztah (3.61) je v této soustavě obvykle zapisován ve tvaru
 , |
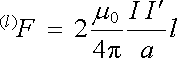(3.62) |
kde
 |
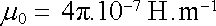(3.63) |
je tzv. permeabilita vakua. (O jednotce henry [H] = [N.m.A-2] = [V.s.A-1] viz článek 4.1.4.) Volbou hodnoty μ 0 je určena i hodnota permitivity vakua ε 0, zavedená vztahem (1.8) , neboť obě tyto konstanty mají bezprostřední vztah k rychlosti šíření světla ve vakuu. (Podrobněji o těchto otázkách viz článek 5.3.1 a Dodatek 2.)
Všimněme si nyní zajímavé vlastnosti magnetického pole přímého vodiče, která souvisí s cirkulací vektoru magnetické indukce, tj. s vyšetřováním křivkového integrálu
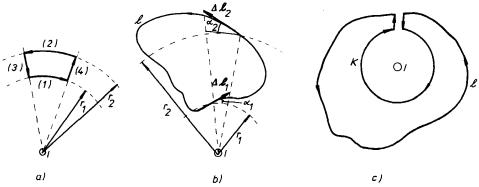
Obr. 3.15 K formulaci Amp`erova zákona. Výpočet cirkulace vektoru magnetické indukce po křivkách neobepínajících vodič: a) speciální tvar křivky, b) obecná křivka, c) výpočet cirkulace vektoru magnetické indukce po křivce obepínající vodič.
 |
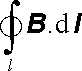(3.64) |
po libovolné uzavřené křivce l (viz Dodatek l). Zvolme nejdříve speciální tvar rovinné křivky l1 sestávající ze dvou oblouků (1), (2) kružnic koncentrických s osou vodiče a ze dvou radiálních úseků (3), (4) (viz obr. 3.15a). Úseky (3), (4) k hodnotě integrálu (3.64) nepřispívají, neboť na nich je B ⊥ dl . Příspěvky úseků (l), (2) se navzájem odečítají, neboť délky úseků jsou v poměru r2/r1 a velikosti magnetické indukce jsou podle (3.60) v poměru obráceném, přičemž orientace těchto úseků jsou opačné vzhledem k orientaci vektoru B . Celkem tedy platí
 |
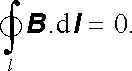(3.65) |
Získaný výsledek je možné zobecnit i na uzavřenou křivku obecného tvaru, rovinnou i prostorovou, pokud tato křivka nebude obepínat vyšetřovaný vodič . Vytneme-li totiž na takové křivce dvěma radiálními paprsky dva diferenciální úseky Δ l1, Δ l2 (viz obr. 3.15b), potom délky těchto úseků budou v poměru
 |
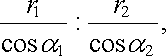zatímco projekce vektoru B do směru tečny budou v poměru obráceném.
Naopak, budeme-li hledat hodnotu integrálu (3.64) podél kružnice K poloměru r v rovině kolmé k vodiči, se středem v jeho ose, bude zřejmě platit podle (3.60) a (3.63)
 |
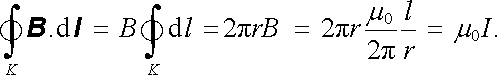(3.66) |
V případě křivky l obecného tvaru můžeme při vyšetřování integrálu (3.64) použít postup analogický k postupu použitému při formulaci Gaussova zákona (viz čl. 1.2.2). Zvolíme pomocnou kružnici K se středem na ose vodiče a vytvoříme sjednocení obou křivek K + l tak, aby příspěvky úseků tvořících spojení obou křivek bylo možné zanedbat (nebo aby se vyrušily) - viz obr. 3.15c. Celková křivka K + l neobepíná vodič a integrál (3.64) podél ní je tedy roven nule. Vzhledem k tomu, že obě křivky K, l jsou opačně orientované, platí
 |
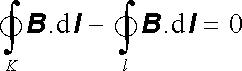(3.67) |
a hodnota integrálu (3.64) podle obecné křivky l je tedy opět rovna μ 0I. Celkem lze tedy říci, že pro integrál (3.64) přes libovolnou uzavřenou křivku l platí
 |
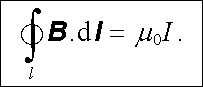(3.68) |
Experimentální zkušenost ukazuje, že vztah (3.68) platí obecně pro libovolné magnetické pole (tj. pro libovolný tvar vodičů protékaných proudem) a pro libovolnou uzavřenou křivku l. Křivkový integrál typu (3.64) počítaný přes libovolnou uzavřenou křivku je vždy roven μ 0-násobku proudu, který protéká plochou ohraničenou touto křivkou. (Přesně vzato, toto tvrzení platí pouze tehdy, je-li křivka jednoduchá. V případech, kdy křivka obíhá daný vodič například N-krát, vystupuje na pravé straně (3.68) N-násobek proudu I.)
Vztah (3.68) vyjadřuje jednu ze základních vlastností magnetického pole. Nazývá se Amp`erův zákon (někdy též zákon celkového proudu). Je z něj vidět, že magnetické pole není obecně potenciální. Křivkový integrál (3.68) obecně závisí na tvaru a poloze uzavřené křivky l. Pouze ve speciálních případech, kdy křivka neobepíná makroskopický proud, je příslušný integrál nulový (srov. čl. 3.4.4). Amp`erův zákon vyjádřený vztahem (3.68) udává souvislost mezi hodnotami magnetické indukce a proudy, které ji vytváří, v implicitním a integrálním tvaru.
Na platnost tohoto vztahu nejsou kladena žádná fyzikální omezení. Je proto nutné předpokládat, že ve všech případech, kdy křivkový integrál (3.64) má smysl, splňuje podmínku (3.68) . Proud na pravé straně tohoto vztahu může být realizován libovolným způsobem. S ohledem na rovnici kontinuity, která ve stacionárním přiblížení platí ve tvaru (3.16) , resp. (3.17) , může být pro výpočet tohoto proudu zvolena libovolná plocha S ohraničená křivkou l. Amp`erův zákon (3.68) má pro popis magnetického pole analogický význam jako Gaussův zákon pro popis pole elektrostatického (srov. rovnici (1.73) a výklad čl. 1.2.5).
Výraz (3.68) je možné převést na diferenciální tvar. Předpokládejme, že na ploše S zvolené pro výpočet proudu I netečou žádné plošné proudy. Proud I je potom určen pouze hustotou objemového proudu j (r ), takže platí
 |
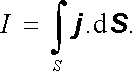(3.69) |
Po dosazení do (3.68) a po použití Stokesovy věty (viz Dodatek 1) můžeme Amp`erův zákon vyjádřit pomocí plošného integrálu
 . |
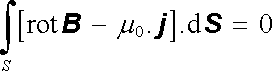(3.70) |
Vzhledem k libovolnosti plochy S, vyplývá z (3.70) podmínka
 |
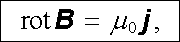(3.71) |
která tedy platí ve všech bodech s nulovou hustotou plošného proudu a která představuje diferenciální formu Amp`erova zákona.
V kapitole l jsme viděli, že cirkulace intenzity elektrostatického pole a její tok uzavřenou plochou určují obecné vlastnosti elektrostatického pole. Podobně v předchozím článku bylo ukázáno, že vyšetřování cirkulace magnetické indukce vede na formulaci Amp`erova zákona, který rovněž vyjadřuje jednu z obecných vlastností magnetického pole. Vzniká proto přirozeně otázka, jakou informaci o magnetickém poli může dát vyšetřování toku vektoru magnetické indukce uzavřenou plochou.
Tok vektoru magnetické indukce, nebo krátce magnetický tok Φ , je pro danou plochu S definován vztahem (3.59) . Veškerá dosavadní experimentální zkušenost ukazuje, že magnetický tok libovolnou uzavřenou plochou S je roven nule.
 |
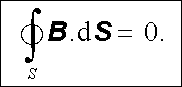(3.72) |
Analogickým postupem jako v článku 1.2.5 (srov. Dodatek l) je možné vlastnost (3.72) vyjádřit též v diferenciálním tvaru
 |
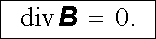(3.73) |
Na platnost vztahu (3.72) nejsou kladena žádná fyzikální omezení. Je možné jej uvažovat ve všech situacích, ve kterých má integrál na levé straně smysl. Podobně podmínku (3.73) je možné uvažovat ve všech bodech, ve kterých mají smysl příslušné operace. Oba tyto vztahy vyjadřují experimentální poznatek, že v přírodě neexistují "magnetické náboje", které by tvořily zdroje magnetického pole.[20] Magnetické indukční čáry, jimiž je možné magnetické pole zobrazovat (podobně jako elektrické pole siločarami - viz čl. 1.2.1), jsou tedy vždy uzavřené křivky.
P. A. M. Dirac v roce 1931 předpověděl teoreticky možnost existence elementární částice, která by byla nositelem magnetického náboje (tzv. Diracův magnetický monopól). Přes značné úsilí, které pokračuje i v současné době s využitím nejmodernějších experimentálních metod, však dosud nebyla existence takové částice experimentálně potvrzena. O teoretických důvodech vedoucích k možnosti existence Diracova magnetického monopólu pojednává například [3].
Platnost vztahů (3.68) a (3.72) ukazuje, že magnetické pole je polem sole-noidálním (viz Dodatek 1). Magnetickou indukci lze tedy vyjádřit pomocí nového vektorového pole A ( r ) vyhovujícího vztahu
 , |
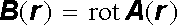(3.74) |
které se nazývá vektorovým potenciálem magnetického pole.
Definiční relace (3.74) však neurčuje vektorový potenciál jednoznačně. Je zřejmé, že pokud existuje alespoň jedna funkce A (r ) vyhovující (3.74) , vyhovuje tomuto vztahu také každá vektorová funkce tvaru
 , |
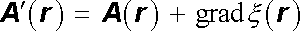(3.75) |
kde &ksi; (r ) je libovolná skalární funkce, pro niž existují příslušné diferenciální operace. Uvědomíme-li si totiž, že pro libovolnou funkci &ksi; (r ) platí identita rot grad &ksi; (r ) = 0 (viz Dodatek l), dostaneme
 |
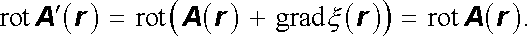Tato nejednoznačnost dovoluje předepsat pro vektorový potenciál vedlejší podmínku. Speciálně je vždy možné vektorový potenciál vybrat tak, aby byla splněna podmínka
 |
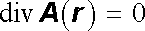(3.76) |
nazývaná podmínkou kalibrační. Skutečně, platí-li pro daný vektorový potenciál vyšetřovaného magnetického pole například divA (r ) = α (r ), kde α (r ) je nenu-lová skalární funkce, lze k němu superponovat funkci grad &ksi; vyhovující rovnici div grad &ksi; (r ) = Δ &ksi; (r ) = -α (r ); nový vektorový potenciál pak již kalibrační podmínce (3.76) vyhovuje.[21]
Využijeme nyní vlastnosti vektorového potenciálu k vyjádření dalších obecných zákonitostí magnetického pole. Amp`erův zákon (3.71) lze pomocí vektorového potenciálu zapsat ve tvaru
 |
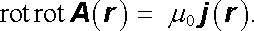(3.77) |
Využitím identity vektorové analýzy (D 1.58) pak pro něj dostaneme
 |
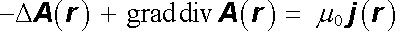(3.78) |
a díky kalibrační podmínce (3.76) máme vektorovou rovnici
 |
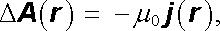(3.79) |
která představuje vlastně trojici Poissonových rovnic pro jednotlivé složky vektorů A ( r ) , j ( r ) (srov. čl. 1.2.7). V analogii s elektrostatikou můžeme její řešení psát zřejmě ve tvaru
 |
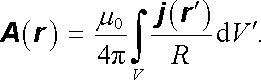(3.80) |
Vektor R zde má opět svůj známý význam R = r - r ℜ' . Integrační proměnnou je polohový vektor r a integrujeme přes objem V, ve kterém je j ( r ℜ' ) ℜ ≠ 0.
Přímým provedením operace rotace na funkci (3.80) dostaneme vyjádření pro magnetickou indukci
 |
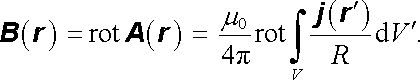Operace rotace a integrace působí na různé proměnné. Budeme (jako vždy) předpokládat možnost záměny jejich pořadí. Kromě toho vezmeme v úvahu platnost identity
 |
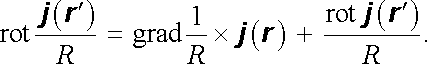Druhý člen pravé strany je identicky nulový, neboť hustota proudu není funkcí proměnné r , na kterou působí operátor rotace. Přímým výpočtem dále zjistíme, že
 |
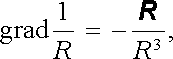takže pro vyjádření magnetické indukce získáme konečný výraz
 |
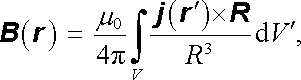(3.81) |
který se obvykle nazývá Biotovým-Savartovým vzorcem.
Vzorec (3.81) (na rozdíl od Amp`erova zákona) vyjadřuje souvislost mezi vektorem magnetické indukce a proudy, tvořícími zdroj magnetického pole, v explicitní formě. Tento vzorec a vzorec (3.80) pro vektorový potenciál jsou zřejmě analogické vzorcům (1.70a) , popř. (1.69a) , pro potenciál, popř. intenzitu elektrostatického pole spojitě rozložených nábojů. Z tvaru Biotova-Savartova vzorce lze výsledné magnetické pole v daném bodě chápat jako superpozici příspěvků jednotlivých "proudových elementů" j Δ V. Lze tedy - podobně jako v elektrostatice - hovořit o platnosti principu superpozice. Je ovšem samo-zřejmé, že "proudový element" nelze izolovat. Platnost Biotova-Savartova vzor-ce a principu superpozice může být tudíž ověřována jen nepřímo, měřením výsledného pole uzavřených proudových smyček různého tvaru.
Pro vyšetřování magnetického pole vodičů zanedbatelně malého průřezu Δ S s homogenně rozloženým proudem I je výhodné vyjádřit vzorec (3.81) v poněkud jiném tvaru. Malý úsek vodiče délky Δ l reprezentuje zřejmě "proudový element" IΔ l ekvivalentní s j Δ V (srov. vztah (3.6) ). Záměnou těchto elementů lze objemový integrál v (3.80) a (3.81) zřejmě převést na křivkový integrál podél proudové trubice l s daným proudem I. Tedy
 . |
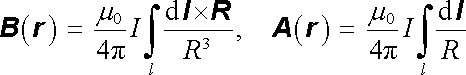(3.82) |
Je-li zdroj magnetického pole tvořen několika proudovými smyčkami (proudovými trubicemi), je výsledné pole zřejmě dáno sumou integrálů typu (3.82) .
Vzorce typu (3.81) a (3.82) pro vyjádření magnetického pole vodičů protékaných proudem byly původně získány zobecněním experimentální zkušenosti. V literatuře bývají proto často nazývány Biotovým-Savartovým zákonem. Byly formulovány roku 1820 na základě měření, které konali jeho autoři na vodičích různého tvaru; o obecnou formulaci výsledků se zasloužil P. Laplace (srov. Historický přehled).
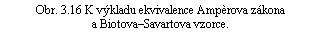
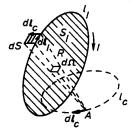
Biotův-Savartův vzorec jsme odvodili z Amp`erova zákona. Lze jej však považovat za poznatek k Amp`erovu zákonu ekvivalentní, neboť lze obráceně, na základě platnosti Biotova-Savartova vzorce, odvodit i platnost Amp`erova zákona. Pro demonstraci této možnosti budeme uvažovat magnetické pole buzené proudovou smyčkou lI s proudem I a budeme počítat jeho cirkulaci po uzavřené křivce lc obepínající vodič smyčky lI (viz obr. 3.16). Nechť je podle předpokladu magnetická indukce B , vybuzená smyčkou lI v libovolném bodě A křivky lc, dána vztahem (3.82) . Pro uvažovanou cirkulaci pak dostaneme
 |
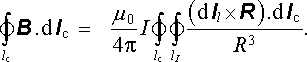Aniž bychom se zabývali matematickou stránkou naznačené dvojnásobné integrace po křivkách lc a lI, můžeme uvést jednoduchou úvahu, z níž její výsledek vyplývá. Cyklickou záměnou veličin smíšeného součinu dostaneme (dl I ℜ × R ).dl c = (dl c ℜ × dl I ).R = dS . R , kde dS = dl c ℜ × dl I . Zavedeme-li element prostorového úhlu dΩ , pod nímž je z bodu A na křivce lc vidět element plochy dS, můžeme celý výraz za integračními značkami vyjádřit ve tvaru
 |
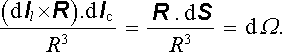Výsledek naznačené integrace pak zřejmě představuje celkovou změnu prostorového úhlu, pod nímž vidíme smyčku lI, jestliže bod A oběhne celou uzavřenou křivku lc. Obepíná-li křivka lc vodič tvořený smyčkou lI, je tato změna rovna plnému prostorovému úhlu 4π . Platí tedy
 |
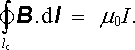(3.68a) |
Alternativně lze tento výsledek získat i využitím ekvivalence proudové smyčky a homogenní magnetické dvojvrstvy s danou konstantní hustotou dipólového momentu MS (viz čl. 3.4.5), vyplňující libovolnou plochu Sl, ohraničenou křivkou lI (viz obr. 3.16), je-li splněna podmínka (3.125) . Vyšetřované magnetické pole je pak možné popsat skalárním potenciálem, viz rov. (3.126) ,
 |
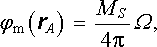kde Ω je prostorový úhel, pod nímž je dvojvrstva vidět z bodu A. Podle (3.120) je možné hledanou cirkulaci vyjádřit ve tvaru
 . |
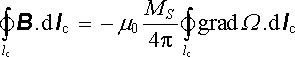Jelikož při průchodu plochou Sl má potenciál φ m nespojitost velikosti MS, platí podle (3.126)
 |
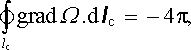odkud již s ohledem na (3.125) ihned plyne (3.68) .
Pomocí vektorového potenciálu jsme získali pozoruhodné výsledky. Viděli jsme, že základní rovnici magnetického pole (3.70) , která je vyjádřena pomocí Amp`erova zákona, můžeme přepsat do tvaru analogického Poissonově rovnici (1.85) . Jejím řešením je pak možné najít integrální vztahy (3.80) až (3.82) pro explicitní vyjádření vektorového potenciálu a magnetické indukce. Podmínkou pro platnost těchto získaných závěrů ovšem je, aby řešení rovnice (3.79) bylo také řešením rovnice (3.77) , a tedy i řešením rovnice (3.71) . To bude splněno, bude-li vektorový potenciál (3.80) splňovat kalibrační podmínku (3.76) . Přímým výpočtem (viz například [6]) lze snadno ukázat, že uvedená vlastnost je důsledkem rovnice kontinuity proudu ve stacionárním přiblížení (3.17) . Lze tedy uzavřít, že pro danou stacionární soustavu vodičů protékaných proudem vektorový potenciál požadovaných vlastností[22] vždy existuje a může být v principu vždy vypočten pomocí vztahů typu (3.80) až (3.82) .
Vektorový potenciál je rovněž vhodnou veličinou pro vyjádření magnetického toku Φ danou plochou S. Alternativně k definičnímu vztahu (3.59) lze použitím Stokesovy věty (D 1.45) vyjádřit magnetický tok Φ pomocí křivkového integrálu
 |
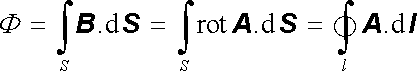(3.59a) |
přes uzavřenou křivku l obepínající plochu S. Magnetický tok je tedy zcela určen, pokud známe průběh vektorového potenciálu jen na hranicích této plochy S.
Ze způsobu zavedení vektorového potenciálu vyplývá, že z hlediska klasické fyziky představuje vedle magnetické indukce alternativní a fyzikálně zcela ekvivalentní veličinu pro popis makroskopického magnetického pole. Na tomto závěru nemění nic ani skutečnost, že vektorový potenciál není silovými účinky magnetického pole určen jednoznačně, a ani to, že v některých případech je třeba vektorový potenciál považovat za různý od nuly v místech s nulovou magnetickou indukcí (viz příklad 3.3.5e). O volbě konkrétního postupu při vyšetřování daného magnetického pole mohou rozhodnout praktické důvody, například obtížnost výpočtu příslušných integrálů či skutečnost, že výrazy pro vektorový potenciál v některých případech divergují, zatímco výrazy pro magnetickou indukci konvergují (viz článek 3.3.5). Pomocí vektoru magnetické indukce lze ovšem bezprostředněji vyjádřit síly působící na vodiče protékané proudem, nebo na pohybující se částice. V kapitole 6 naopak uvidíme, že vektorový potenciál je (obecně řečeno) vhodnější veličinou pro vyjádření energie či hybnosti nabité částice v magnetickém poli.
Ekvivalence obou způsobů popisu magnetického pole přestává být však zřejmá při studiu působení magnetického pole na mikročástice, zejména v případech, kdy je třeba brát v úvahu zákonitosti kvantové mechaniky. Některá hle-diska této problematiky budou ještě diskutována v článku 4.1.2 a v oddílu 6.1.
Výsledky integrace ve vztazích (3.80) až (3.82) lze chápat jako vlastní hodnoty integrálu, pokud počítáme magnetické pole v bodech s nulovou hustotou proudu. Uvedené výrazy je však možné za určitých podmínek použít i k výpočtu magnetického pole v bodech, v nichž je j (r ℜ' ) ℜ ≠ 0. Jelikož vzorce (3.80) a (3.81) , vyjadřující vektorový potenciál a magnetickou indukci magnetického pole makroskopického proudu o hustotě ρ (r ℜ' ), jsou formálně shodné se vzorci (1.70a) a (1.69a) pro potenciál a intenzitu elektrostatického pole spojitě rozloženého náboje o objemové hustotě ρ (r ℜ' ), je možné tyto podmínky diskutovat zcela analogicky jako v elektrostatice (viz článek 1.2.4).
Za předpokladu, že funkce j (r ℜ' ) je konečná a dostatečně hladká ve všech vnitřních bodech oblasti V, lze shrnout vlastnosti výrazů (3.80) a (3.81) takto:
1. Vztah (3.80) vyjadřuje konečný vektorový potenciál magnetického pole objemových proudů ve všech bodech prostoru , tedy i v bodech oblasti V, v nichž je od nuly různá hustota objemového proudu j (r ℜ' ).
2. Tento potenciál je všude spojitý a má parciální derivace alespoň prvního řádu.
3. Veličina B (r ) = rot A (r ) je rovna objemovému integrálu (3.81) ve všech bodech prostoru. Tento vzorec vyjadřuje tedy správně magnetickou indukci pole i uvnitř oblasti V.
4. Magnetická indukce daná vztahem (3.81) je všude spojitá.
V některých situacích (například při vyšetřování magnetického pole v látkách - viz oddíl 3.5) má význam studovat magnetické pole makroskopických plošných proudů. Je-li dána hustota plošného proudu j S (r ℜ' ) tekoucího na ploše S, je zřejmě možné vyjádřit vektorový potenciál a magnetickou indukci příslušného pole vzorci analogickými k (1.70b) a (1.69b) . Je tedy možné psát
 , |
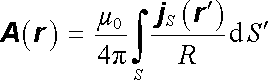(3.80a) |
 . |
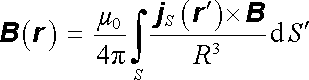(3.81a) |
Vzhledem k formální shodnosti těchto vztahů se vzorci (1.70b) a (1.69b) pro potenciál a intenzitu elektrostatického pole plošně rozložených nábojů, je možné analogicky k článku 1.2.4 formulovat vlastnosti magnetického pole plošných proudů, včetně jeho chování v bezprostředním okolí plochy S. Za analogických předpokladů o vlastnostech funkce j S (r ℜ' ) platí:
1. Výraz (3.80a) vyjadřuje konečný vektorový potenciál ve všech bodech prostoru, tedy i v bodech plochy S, v nichž je od nuly různá hustota proudu j S (r ℜ' ).
2. Tento potenciál je všude spojitý. Má parciální derivace alespoň prvního řádu v bodech neležících na ploše S.
3. Vektor magnetické indukce B (r ) = rot A (r ) je roven plošnému integrálu (3.81a) ve všech bodech s výjimkou bodů plochy S. Na této ploše nemá vektor magnetické indukce smysl.
4. Magnetická indukce daná výrazem (3.81a) je spojitá všude s výjimkou bodů plochy S. Při průchodu touto plochou zůstávají spojité pouze její normálové složky Bn. Její tečné složky se mění skokem o hodnotu určenou hustotou proudu j S (r ℜ' ). Platí vztahy
 |
(3.83) |
 |
(3.84) |
v nichž n je jednotkový vektor normály plochy S, orientovaný ze strany (2) k (l) - viz obr. 3.17.
Alternativní možnost pro vyjádření vztahů (3.83) a (3.84) dávají operace "Div" a "Rot" zavedené v Dodatku l (srov. vztahy (1.80) a (1.82) )
 |
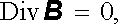(3.83a) |
 |
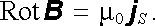(3.84a) |
Tyto vztahy lze dokázat přímo diskusí vlastností plošných integrálů (3.80a) a (3.81a) . Lze je však také snadno dokázat využitím obecných vlastností magnetického pole daných rovnicemi (3.68) a (3.72) . Spojitost normálových složek vektoru magnetické indukce je triviálním důsledkem rovnice (3.72) . Abychom se o tom přesvědčili, stačí obklopit vyšetřovaný bod na ploše S malou válcovou ploškou o podstavách , jejíž osa je rovnoběžná s normálou plochy S (srov. obr. 1.14). Z nulovosti celkového magnetického toku touto ploškou pak ihned plyne vlastnost (3.83) .
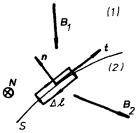
Pro důkaz vlastností tečných složek (3.84) uvažujme orientovanou uzavřenou křivku tvaru obdélníčku, která obklopuje vyšetřovaný bod na ploše S, jak je naznačeno na obr. 3.17. Delší strany obdélníčku nechť jsou rovnoběžné s libovolně zvoleným jednotkovým tečným vektorem t . Jeho kratší strany nechť jsou kolmé k ploše S, tj. rovnoběžné s jednotkovým vektorem normály n . Zaveďme ještě jednotkový vektor N = n ℜ × t a aplikujme na obvod obdélníčku rovnici (3.68) . Celkový proud protékající jeho plochou bude mít zřejmě hodnotu jSNΔ l = (j .N )Δ l. Pro křivkový integrál (3.64) dostaneme po zanedbání příspěvků kratších stran obdélníčku přibližnou hodnotu (B 1 - B 2).t Δ l. Bude tedy platit
 . |
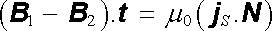Jelikož je
 |
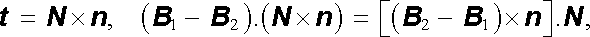lze výsledek zapsat ve tvaru
 . |
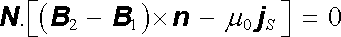Orientace tečného vektoru t byla zvolena libovolně. Poslední podmínka může tedy platit jen tehdy, je-li výraz v hranaté závorce roven nule, tj. platí-li (3.84) .
V tomto článku shrneme obecné zásady pro výpočet magnetické indukce, respektive vektorového potenciálu magnetického pole buzeného zadanými makroskopickými proudy v okolním prázdném prostoru. Obecný výklad dopl-níme několika typickými a z praktického hlediska užitečnými příklady.
l. Je-li zadána hustota objemového proudu j (r ℜ' ), hustota plošného proudu j S (r ℜ' ), nebo je-li znám proud I protékající zadaným obvodem, je vždy možné vypočítat magnetickou indukci B (r ) a vektorový potenciál příslušného pole A (r ) v explicitní formě pomocí vzorců Biotova-Savartova typu (3.80) až (3.82) , respektive (3.80a) a (3.81a) . Přitom můžeme počítat buď A (r ) i B (r ) nezávisle na sobě, nebo integrovat příslušný vzorec pro A (r ) (což v některých případech bývá snazší) a pak určit magnetickou indukci podle (3.74) . O volbě konkrétního postupu rozhodne obtížnost výpočtu jednotlivých integrálů. Přitom může nastat situace, že integrál pro A (r ) diverguje, zatímco integrál pro B (r ) konverguje.
2. Pokud prostorové rozložení proudu je symetrické, je nejvýhodnější použít Amp`erova zákona v integrálním tvaru (3.68) . Stačí najít uzavřenou křivku l procházející daným bodem a obepínající zadaný proud I tak, aby vektor magnetické indukce na této křivce měl tečný směr a konstantní velikost B. Potom platí
 . |
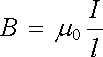(3.85) |
3. Jde-li o geometricky nepravidelné nebo komplikované rozložení proudů, mohou se předchozí způsoby ukázat nepoužitelné nebo příliš pracné. Jak bude ukázáno v následujícím oddílu 3.4, lze pak na vzdálenostech mnohem větších, než je rozměr oblasti s nenulovým proudem, určovat průběh vektorového potenciálu či magnetické indukce přibližně, pomocí tzv. multipólového rozvoje (viz článek 3.4.3). Přitom je obvykle možné vystačit s dipólovým, nejvýše s kvadrupólovým členem.
Průběh magnetické indukce přímého nekonečné dlouhého vodiče jsme již částečně diskutovali při formulování Amp`erova zákona v čl. 3.3.2. Zjistili jsme, že vektor B leží v rovině kolmé k ose vodiče a má v každém bodu směr tečny kružnice se středem v ose vodiče. Závislost jeho velikosti na vzdálenosti a od osy vodiče je dána vztahem typu (3.60) . Tento vzorec bychom nyní snadno získali použitím Amp`erova zákona. Kdybychom za uzavřenou křivku l zvolili kružnici o poloměru a se středem v ose vodiče, mohli bychom s ohledem na symetrii soustavy psát podle Amp`erova zákona (viz vztah (3.85) ) Bl = 2B = 0I, odkud plyne ihned výsledek
 . |
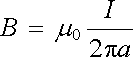(3.86) |
Užitím Amp`erova zákona je možné vypočítat průběh magnetického pole také uvnitř vodiče. Předpokládejme, že vodič má poloměr a0, a zvolme uzavřenou křivku lℜ' ve tvaru kružnice se středem v ose vodiče a s poloměrem a ℜ ≤ a0. Za předpokladu, že proud je rovnoměrně rozdělen po celém průřezu vodiče, můžeme vypočítat proud I ℜ' protékající plochou kružnice
 |
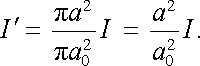Užitím Amp`erova zákona pak pro magnetickou indukci máme
 |
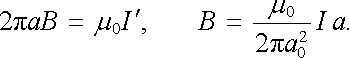(3.87) |
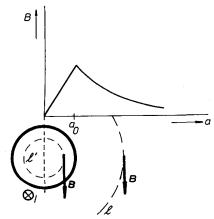
Vidíme, že v souhlasu se závěry předchozího článku je její průběh na povrchu vodiče spojitý (viz obr. 3.18).
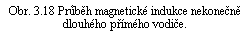
Pro ilustraci použití Biotova-Savartova vzorce k výpočtu magnetického pole odvodíme vzorec (3.86) ještě jednou pomocí vztahu (3.82) . Uvažujme velmi tenký vodič protékaný proudem podle obr. 3.19. Zvolme počátek soustavy souřadné O v patě kolmice spuštěné na vodič z bodu, ve kterém počítáme pole. Dosazením do (3.82) obdržíme pro velikost vektoru magnetické indukce vzbuzené úsekem vodiče AB
 |
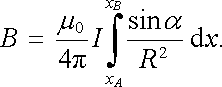Uvážíme-li, že
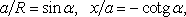můžeme dále počítat
 |
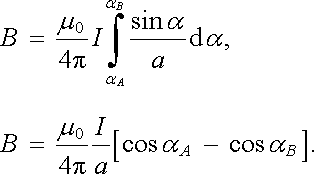(3.88) |
Odtud pro limitní případ nekonečně dlouhého vodiče, kdy platí cosα A ℜ → 1, cosα B ℜ → -1, okamžitě plyne výsledek (3.86) .
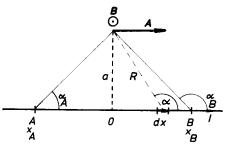
Využitím (3.82) lze podobným způsobem vypočítat i vektorový potenciál A . V našem případě má proudový element IΔ l neproměnný směr totožný se směrem vodiče orientovaným směrem protékajícího proudu. Směr a orientace vektorového potenciálu je tudíž dána směrem vodiče a orientací proudového elementu (viz obr. 3.19). Pro velikost vektorového potenciálu připadajícího na úsek vodiče AB podle (3.82) vychází
 |
 |
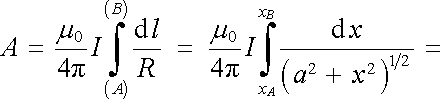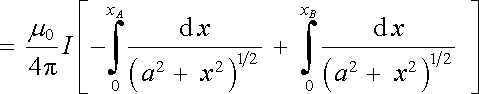a odtud
 . |
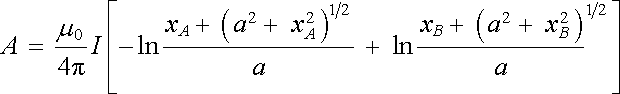(3.89) |
Limitování pro nekonečně dlouhý vodič není v tomto případě možné, neboť výsledek pro | xA | , | xB | ℜ → ℜ nekonecno diverguje.
Získaný výsledek
může být zpětně použit k výpočtu magnetické indukce pomocí
(3.74)
. Jelikož je
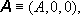platí
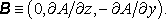Pro obě nenulové složky tudíž dostáváme
 |
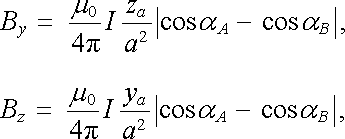(3.90) |
přičemž jsme označili
,
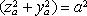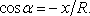Využitím tohoto výsledku již snadno vypočteme
velikost magnetické indukce danou vztahem
(3.88)
.
K řešení této úlohy je výhodné použít Biotova-Savartova vzorce. Z uspořádání na obr. 3.20 je vidět, že výsledná magnetická indukce je rovnoběžná s osou závitu, neboť kolmé složky příspěvků buzených symetricky položenými elementy se vzájemně ruší. Můžeme proto počítat přímo složku Bz, pro niž se křivkový integrál (3.82) redukuje na elementární integraci. Jelikož je cosβ = a/r, platí v označení podle obrázku
 |
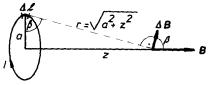
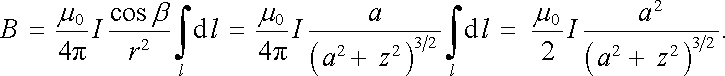(3.91) |
Pole ve středu závitu dostaneme, dosadíme-li do (3.91) z = 0
 . |
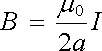(3.92) |
Cívku, jejíž závity jsou navinuty v jedné vrstvě těsně vedle sebe na válcové ploše, nazýváme solenoidem. Na obrázku 3.21 je zobrazen solenoid délky l a poloměru a. Předpokládejme, že na jeho jednotkovou délku připadá Nl závitů. Vypočítáme velikost vektoru magnetické indukce B v libovolném bodě O na jeho ose.
Úlohu nejsnáze vyřešíme, použijeme-li principu superpozice a výsledku předchozího příkladu. Uvedené pole bude dáno součtem příspěvků jednotlivých závitů. Uvážíme-li, že na délku vinutí Δ z připadá NlΔ z závitů, které přispívají k celkové hodnotě magnetické indukce příspěvkem
 |
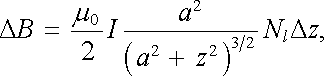bude výsledná hodnota dána integrálem
 |
(3.93) |
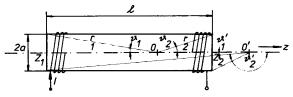
Výsledek bude názornější, uvážíme-li, že pro úhly
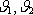vyplývají z obrázku vztahy
 |
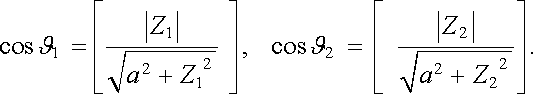Dostaneme
 |
(3.94) |
Pro body uvnitř solenoidu jsou oba úhly ϑ 1, ϑ 2 ostré, takže hodnoty obou kosinů jsou kladné. Leží-li však bod, ve kterém počítáme pole, vně solenoidu (např. bod O' na obrázku), je jeden úhel tupý a příslušný kosinus má zápornou hodnotu. Ve speciálním případě velmi dlouhého solenoidu bude cosϑ 1 = 1, cosϑ 2 = 1. Vzorec (3.94) se redukuje na známý jednoduchý tvar
 . |
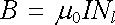(3.95) |
Uvažujme cívku podle obr. 3.22. Závity cívky z velmi tenkého vodiče o celkovém počtu N nechť jsou navinuty na kostře ve tvaru prstence, v jedné vrstvě těsně vedle sebe po celém jejím obvodu; proud I tekoucí cívkou má pak vlastnosti plošného proudu rovnoměrně rozloženého na plášti prstence. Střední poloměr prstence nechť je R0. Vypočítejme hodnotu magnetické indukce B uvnitř prstence.
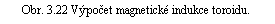
Vzhledem k symetrii soustavy lze soudit, že magnetické indukční čáry jsou kružnice ležící v rovinách kolmých k ose symetrie solenoidu, se středy na této ose. Z podobných důvodů je nutné dále soudit, že magnetická indukce má stejnou hodnotu ve všech bodech dané indukční čáry. Zvolíme-li proto za integrační dráhu libovolnou indukční čáru délky l, bude podle Amp`erova zákona platit
 , |
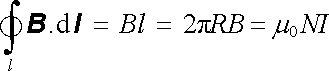kde R je poloměr této čáry.
Kružnice, které jsou vedeny vně toroidu (např. kružnice k1, k3 na obrázku), neuzavírají žádný proud, takže platí Bl = 0. Magnetická indukce vně toroidu je tedy nulová. Leží-li naopak indukční čára, podle níž se integruje, uvnitř prstence platí
 . |
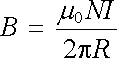(3.96) |
V praktických
aplikacích je častý případ, kdy rozměr d je
mnohem menší než střední poloměr R0,
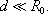(viz kružnici k2 na obr.
3.22). Pak platí
 |
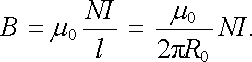(3.97) |
Magnetická indukce má tedy pro tento případ v celém vnitřním objemu toroidu přibližně stejnou velikost danou vztahem (3.97) .
Z tohoto vztahu můžeme také získat výraz (3.95) pro magnetickou indukci velmi dlouhého solenoidu. Uvědomíme-li si, že poměr N/l = Nl představuje počet závitů připadající na jednotkovou délku, dostaneme zmíněný výraz. Nekonečně dlouhý solenoid můžeme chápat jako toroid o nekonečném poloměru. Z postupu, kterým byl vzorec (3.97) získán, ovšem plyne, že magnetické pole uvnitř nekonečného solenoidu je homogenní. Vzorec (3.95) udává tedy jeho hodnotu nejen na ose.
Úloha o nalezení vektorového potenciálu k danému průběhu magnetické indukce znamená nalézt vektorové pole A (r ), které vyhovuje definičnímu vztahu (3.74) , eventuálně kalibrační podmínce (3.76) . Předpokládejme nejdříve, že dané homogenní pole B 0 je vytvářeno blíže nespecifikovanými zdroji a vyplňuje celý prostor. Přímým výpočtem se snadno přesvědčíme, že vektorový potenciál
 |
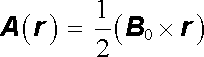(3.98) |
vyhovuje uvedeným podmínkám, tj. definiční relaci (3.74) , i kalibrační podmínce (3.76) . Zvolíme-li speciální pravoúhlou soustavu souřadnou například tak, že osu z položíme do směru pole B 0 ℜ ≡ (0, 0, B0), můžeme vektorový potenciál (3.98) vyjádřit ve složkách. Platí
 |
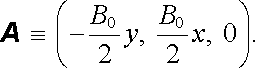(3.98a) |
Snadno se přesvědčíme, že pro dané homogenní pole B
0 vyhovují podmínkám
(3.74)
a
(3.76)
i vektorová pole
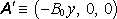a
,
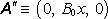za jejichž superpozici můžeme (až na velikost) vektorový potenciál
(3.98)
považovat. Tato skutečnost demonstruje známý poznatek, že vektorový potenciál
není k danému průběhu magnetické indukce (i při splnění kalibrační
podmínky
(3.76)
) určen jednoznačně.
Jedním z možných
způsobů, jak lze homogenní magnetické pole (v ome-zeném objemu) přibližně
realizovat, je velmi dlouhý solenoid. Proto ještě vyšetříme vektorový
potenciál nekonečně dlouhého solenoidu, který ve svém vnitřním objemu vytváří
homogenní pole (srov. příklad 3.3.5d). Je zřejmé, že magnetické pole ve
vnitřním prostoru solenoidu může být popsáno vektorovým potenciálem
(3.98a)
,
položíme-li osu z soustavy souřadné
do osy solenoidu. Ve vzdálenosti r⊥
od osy solenoidu,
,
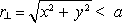kde a je jeho poloměr, lze tedy podle
(3.95)
pro velikost vektorového potenciálu psát
 |
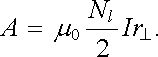(3.99) |
Jeho směr bude zřejmě dán směrem tečny kružnice vedené daným bodem v rovině kolmé k ose solenoidu, se středem na této ose.
Další (a standardní) možnost pro výpočet vektorového potenciálu solenoidu spočívá v přímé aplikaci vzorce (3.82) . Výpočet příslušného integrálu však není zcela jednoduchý a nebudeme jej uvádět.[23] Pro vnitřní prostor nekonečně dlouhého solenoidu vychází opět výsledek (3.99) . Podle článku 3.3.4 však musí existovat vektorový potenciál vyhovující kalibrační podmínce (3.76) , který je spojitý při průchodu vodičem s nenulovou hustotou proudu. Splnění této podmínky pro nekonečně dlouhý solenoid vede k nenulovému vektorovému potenciálu i ve vnějším prostoru, tedy v místech, kde je magnetická indukce nulová (srov. článek 3.3.3). Výpočet pomocí vzorce (3.82) skutečně k nenulovému vektorovému potenciálu ve vnějším prostoru vede. Pro nekonečně dlouhý solenoid poloměru a, vinutý z nekonečně tenkého vodiče, platí v případě r⊥ > a
 |
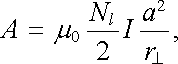(3.100) |
přičemž směr vektoru A leží ve směru tečen souosých kružnic, podobně jako ve vnitřním prostoru.
Snadno se přesvědčíme, že vektorový potenciál podle (3.99) a (3.100) je spojitý pro r⊥ = a, přičemž splňuje kalibrační podmínku (3.76) . Pro r⊥ > a platí B = rot A = 0. Je dále poučné si uvědomit, že vektorový potenciál podle (3.100) , přestože se týká oblasti prostoru s nulovou magnetickou indukcí, umožňuje výpočet magnetického toku danou plochou S, i když tato plocha prochází pláštěm solenoidu. Uvažme například magnetický tok tekoucí plochou souosého kruhu poloměru R0 > a. Je zřejmé, že k tomuto toku přispívá jen magnetické pole B0 uvnitř solenoidu, takže pro něj platí Φ = 2B0. Na druhé straně může být pro výpočet magnetického toku použit vzorec (3.59a) . Díky tomu, že vektorový potenciál je na kružnici tvořící obvod uvažovaného kruhu konstantní a má směr její tečny, platí
 . |
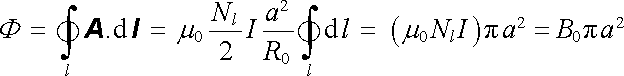Výsledek je nezávislý na poloměru R0, pokud ovšem platí R0 > a.
|
|
|
|
|
|
|
|
|