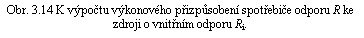Ve stacionárním stavu nezávisí žádná makroskopická veličina na čase. Ve stacio-nárních soustavách může tedy existovat pouze časově neproměnné rozdělení nábojů v prostoru, které je popsáno časově neproměnnou objemovou hustotou. Ve srovnání s elektrostatikou je však situace obecnější v tom, že zatímco některé náboje mohou být v klidu, jiné konají makroskopický pohyb, a realizují tedy stacionární elektrický proud. Jeho hustota j je časově neproměnná a vyhovuje rovnici kontinuity ve tvaru (3.16) , respektive (3.17) . Elektrické pole vytvořené těmito stacionárně rozloženými náboji se nazývá stacionárním elektrickým polem. Vyšetřeme nyní jeho vlastnosti.[17]
Experimentální zkušenost ukazuje, že elektrické stacionární pole je (podobně jako pole elektrostatické) potenciální a konzervativní. Jeho intenzita E (defi-novaná vztahy typu (1.32) , respektive (2.26) ) splňuje tedy v každém bodě podmínku (1.63)
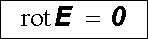 |
a stacionární elektrické pole může být rovněž popsáno pomocí skalárního potenciálu φ (r ); E (r ) = -grad φ (r ).
Fyzikální podstatu konzervativnosti stacionárního pole snadno pochopíme na základě poznatků vyložených v kapitole 2. Jak uvidíme při vyšetřováni elektrické vodivosti různých druhů prostředí v kapitole 7, je makroskopická rychlost nábojů realizujících proud téměř vždy velmi malá ve srovnání s rychlostí světla ve vakuu. Elektrické pole takto pomalu pohybujícího se náboje je dáno vztahem (2.36) , který je formálně shodný s výrazem pro elektrostatické pole bodového náboje. Je tedy zřejmé, že při vyšetřování stacionárního pole není třeba rozlišovat, zda náboje, které pole vytvářejí, jsou v klidu či v pohybu. Makro-skopické stacionární pole, představující střední hodnotu pole nábojů v makro-skopickém stacionárním pohybu, bude tedy časově neproměnné a bude vyho-vovat všem základním rovnicím platným pro pole elektrostatické.
Veškerá dosavadní experimentální zkušenost rovněž ukazuje, že pro elektrické stacionární pole platí i Gaussův zákon, viz (1.73) a (1.77) ,
(eq0027)SETEQ(eq0028)
Podstatný rozdíl mezi oběma typy polí je v tom, že stacionární elektrické pole, na rozdíl od pole elektrostatického, může být trvale nenulové i uvnitř vodičů (ve kterých ovšem teče proud). Úlohy o elektrostatickém a elektrickém stacionárním poli jsou tedy popsány formálně shodnými rovnicemi, liší se však okrajovými podmínkami.
Pro stacionární pole v látkovém prostředí (i uvnitř vodičů) lze zavést vektor elektrické indukce D vztahy analogickými jako v elektrostatice. Platí (1.246) ,
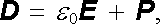 |
kde P je vektor polarizace prostředí. Pro elektricky měkká vodivá prostředí lze zavést i elektrickou susceptibilitu χ e permitivitu ε , takže opět máme[18] , viz (1.255) a (1.258) ,
(eq0030)SETEQ(eq0031)
Pro vektor elektrické indukce platí Gaussův zákon. Pro libovolnou uzavřenou plochu S, ve které je obsažen volný náboj Q, její integrální tvar zní, viz (1.247) ,
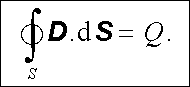 |
V případech, kdy rozložení volného náboje lze v okolí daného bodu popsat objemovou hustotou ρ (r ), je možné známým postupem (viz čl. 1.5.3) získat diferenciální tvar Gaussova zákona (1.248)
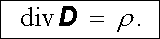 |
Pro zkoumání dalších vlastností stacionárních soustav je již třeba vzít v úvahu konkrétní způsob realizace proudu; v případě proudu kondukčního pak i kon-krétní vlastnosti daného prostředí. V tomto článku se budeme zabývat vlast-nostmi vedení stacionárního proudu ve velké třídě homogenních vodičů.

Je zřejmé, že elektrické pole může být příčinou přemisťování volných nábojů ve vodiči, tedy příčinou vzniku elektrického proudu. Je proto přirozené očekávat, že mezi velikostí intenzity pole (respektive mezi velikostí rozdílu potenciá-lu) a velikostí proudu v daném okamžiku bude existovat vztah, který bude závislý na vlastnostech užitého vodiče. Studiem této závislosti se na počátku devatenáctého století zabýval G. S. Ohm, který na základě experimentů prováděných především na kovech formuloval vztah, který je dnes všeobecně nazýván Ohmovým zákonem a který platí pro velkou třídu homogenních vodičů.
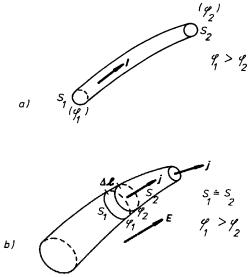
Ohmův zákon říká, že proud I tekoucí v určitém okamžiku daným vodičem je úměrný okamžité hodnotě spádu potenciálu U na tomto vodiči. Pro kvantitativní formulaci Ohmova zákona uvažujme v homogenním izotropním vodiči část proudové trubice, v níž teče proud I, vymezenou dvěma ekvipotenciálními plochami S1, S2 pro jejichž potenciály φ 1, φ 2 platí φ 1 > φ 2 (viz obr. 3.4a). Spádem potenciálu na této části vodiče nazveme kladnou veličinu
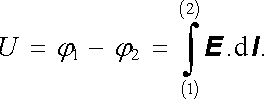 |
(3.18) |
Veličina U vyjadřuje zřejmě napětí plochy S1 o větším potenciálu vůči ploše S2; (srov. čl. 1.2.3). Ohmův zákon je pak zvykem psát ve tvaru
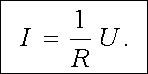 |
(3.19) |
Konstanta R je závislá jednak na geometrickém tvaru vodiče, jednak na druhu látky, z níž je zhotoven. Nazýváme ji elektrickým odporem vodiče.
Elektrický odpor R, definovaný vztahem (3.19) , charakterizuje schopnost vodiče vést elektrický proud. Je vždy považován za kladnou veličinu, čímž je dána orientace vodiče. Za kladný směr ve vodiči je tudíž brán směr poklesu potenciálu. Ohmův zákon ve tvaru (3.18) také říká, že vodiči vždy teče proud ve směru spádu potenciálu.
Pro vzájemné srovnání vlastností různých látek je výhodné zavést veličinu, která nezávisí na tvaru vodiče. Touto veličinou je měrný (specifický) odpor (rezistivita) ρ R, jehož fyzikální smysl snadno pochopíme vyšetřováním poměrů v proudové trubici.
Na libovolnou část proudové trubice vymezenou ekvipotenciálními plochami je možné aplikovat Ohmův zákon. Uvažujme její malou část vymezenou plochami S1, S2 o vzdálenosti Δ l (viz obr. 3.4b) a předpokládejme, že v tomto úseku můžeme průřez S proudové trubice považovat za konstantní. Uvědomíme-li si, že každým průřezem trubice tvořícím ekvipotenciální plochu protéká stejný proud, zjistíme použitím Ohmova zákona, že odpor daného úseku je přímo úměrný délce Δ l a nepřímo úměrný průřezu S. Je-li uvažovaný úsek i průřez S dostatečně malý, můžeme i pro případ nehomogenního vodiče psát známý vztah
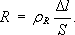 (3.20)
(3.20)
Podle něho vyjadřuje měrný odpor velikost odporu vodiče jednotkové délky a jednotkového průřezu. (Ve shodě s definicí můžeme například říci, že měrný odpor je číselně roven odporu vodiče ve tvaru krychle o jednotkové hraně, jehož protilehlé stěny jsou udržovány na konstantních potenciálech - třeba přiložením vhodných elektrod.) V případě homogenního vodiče o konstantním měrném odporu ρ R lze právě uvedeným postupem jednoduše vyjádřit i odpor R libovolně dlouhého úseku l proudové trubice konstantního průřezu S. Platí analogicky k (3.20)
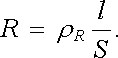 |
(3.20a) |
Kromě odporu a měrného odporu se k charakterizování vlastností látek při vedení elektřiny užívá vodivost G a měrná vodivost (konduktivita) γ . Jsou definovány vztahy
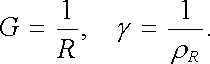 |
(3.21) |
Ohmův zákon vyjádřený ve tvaru (3.19) není vhodný pro obecné úvahy, neboť veličiny v něm vystupující závisí na tvaru uvažovaného vodiče. Užitím pojmu měrného odporu (resp. měrné vodivosti) je však možné získat jeho vyjádření v tzv. diferenciálním tvaru, vyjadřujícím vlastnosti prostředí v daném bodě (srov. čl. 1.2.5). Abychom ho nalezli, uvažujme opět malou část velmi úzké proudové trubice podle obr. 3.4b. Napětí Δ U mezi ekvipotenciálními plochami S1, S2 můžeme vyjádřit pomocí intenzity pole E
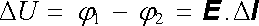 . . |
Proud I tekoucí trubicí lze vyjádřit pomocí hustoty proudu j : I = j . S . Dosadí-me-li tyto hodnoty do (3.19) a vezmeme-li v úvahu, že E i j jsou kolmé k plošce S, dostaneme s ohledem na (3.20) , (3.21) výsledek
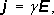 (3.22)
(3.22)
který představuje hledaný diferenciální tvar Ohmova zákona. Vztah (3.22) platí podobně jako (3.19) pro většinu homogenních vodičů a může být také považován za definici měrné vodivosti.
Vztah (3.19) slouží také k odvození jednotek. V Mezinárodní soustavě je jednotkou elektrického odporu jeden ohm (Ω ). Podle (3.19) má vodič odpor jednoho ohmu tehdy, teče-li jím při napětí jednoho voltu proud jednoho ampéru. Jednotkou měrného odporu je podle (3.20) ohm metr (Ω .m). Pomocí vztahů (3.21) lze dále odvodit jednotky vodivosti a měrné vodivosti. Jednotkou vodivosti je ohm na minus první (Ω -1), nazývaný siemens (S). Jednotkou měrné vodivosti je (ohm metr)-1, (Ω .m)-1.
Ohmův zákon je materiálový vztah, který přibližně popisuje chování reálných vodičů v elektrickém poli. V teorii elektrických a magnetických jevů je jeho význam podobný jako význam vztahu (1.255) popisujícího chování měkkého dielektrika v elektrickém poli. Jako každý lineární vztah mezi dvěma různými fyzikálními veličinami může být považován za aproximaci složitější závislostí. Fyzikální podmínky a meze jeho platnosti, které blíže poznáme v kapitole 7, jsou u různých typů vodičů značně rozdílné. Zatímco například v případě homogenních kovů přestává Ohmův zákon zpravidla platit až za velmi extrémních podmínek, existuje řada vodivých prostředí různých skupenství, ve kterých Ohmův zákon v podstatě vůbec neplatí. Nehledě na tyto skutečnosti, má Ohmův zákon zásadní důležitost v teorii elektrických obvodů, neboť definuje pojem lineárního vodiče, v němž se proudy buzené různými příčinami mohou superponovat, aniž by se navzájem ovlivňovaly.
Pro lineární homogenní a izotropní vodič je měrná vodivost (popř. měrný odpor) kladná skalární veličina. V lineárním anizotropním prostředí je měrná vodivost symetrický tenzor druhého řádu. Ohmův zákon v diferenciálním tvaru (3.22) je pak třeba zobecnit. Pro jednotlivé složky hustoty proudu platí
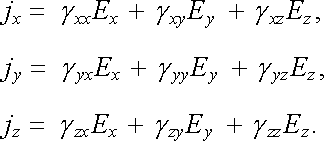 |
(3.23) |
V anizotropním prostředí nejsou tedy vektory j a E obecně kolineární.
Užitím Ohmova zákona lze odvodit některé důležité vlastnosti stacionárního elektrického pole v lineárních vodičích. Především je třeba si uvědomit, že v lineárním, homogenním a izotropním vodiči je hustota proudu vektor, a to vždy kolineární s intenzitou elektrického pole. Dále snadno ukážeme, že v li-neárním homogenním vodiči protékaném stacionárním proudem je hustota volného i vázaného náboje nulová; užitím rovnice kontinuity (3.17) a vztahů (1.248) a (3.22) dostaneme pro objemovou hustotu volného náboje
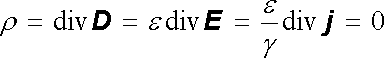 |
(3.24) |
a analogicky pro hustotu náboje vázaného
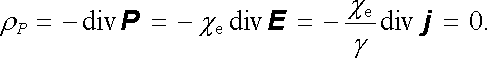 |
(3.25) |
Nenulové makroskopické náboje mohou tedy existovat pouze v místech, ve kterých se mění parametry vodiče.
Dosud jsme probírali vlastnosti stacionárního proudu ve vodiči v souvislosti s vlastnostmi příslušného elektrického pole. Existenci stacionárního proudu jsme předpokládali a nestarali jsme se o podmínky, za kterých tato existence přichází v úvahu. Věnujme se nyní této otázce.
Vzhledem k rovnici kontinuity (3.16) , popř. (3.17) , jsou proudové čáry stacionárního proudu v soustavách konečných rozměrů vždy uzavřené křivky, takže nositelé náboje, realizující tento proud, se musí pohybovat po uzavřených drahách. Takový pohyb, a tudíž ani stacionární proud, nemůže být vyvolán elektrostatickým či elektrickým stacionárním polem, neboť obě tato pole jsou potenciální. Jelikož ze zkušenosti víme, že stacionární proud ve vodiči může existovat, musíme předpokládat existenci jiných, a to nepotenciálních silových polí působících na nositele proudu.
Konkrétní podklady pro vyšetřování takových polí dávají experimenty s nehomogenními vodiči, které ukazují, že Ohmův zákon vyjádřený vztahy (3.19) , popř. (3.22) , pro ně neplatí. Ukazuje se například, že v nehomogenním vodiči může být nulová hustota proudu i při nenulovém poli nebo nenulová hustota proudu při nulovém poli. Tyto výsledky vedou k závěru, že pro nehomogenní vodiče je nutné Ohmův zákon zobecnit. To je možné provést tak, že do vztahu typu (3.22) zahrneme působení žádaných nepotenciálních polí, která jsou obecně neelektrické povahy. (V kapitole 7 budou probrány některé konkrétní formy těchto polí.)
Předpokládáme-li, že zmíněné pole působící na nositele proudu lze popsat silou F *, úměrnou jejich náboji q, je možné v analogii s intenzitou elektrického pole zavést veličinu E * vztaženou k jednotkovému náboji (F * = qE *) a vztah (3.22) zobecnit na tvar
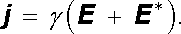 |
(3.26) |
Veličinu E * je zvykem nazývat vtištěnou (elektromotorickou) intenzitou. Ohmův zákon tvaru (3.26) vyhovuje uvedeným experimentálním výsledkům. Hustota proudu je nulová v bodech, ve kterých je E = -E *. V bodech s nulovou inten-zitou pole je proudová hustota j = γ E *.

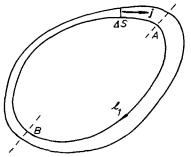
Užitím vztahu (3.26) najdeme nyní odpovídající integrální tvar Ohmova zákona. Vyjádříme křivkový integrál jeho levé i pravé strany podél určité části proudové čáry l1 mezi dvěma ekvipotenciálními plochami A, B (viz obr. 3.5). Dostaneme
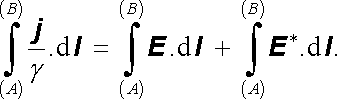 |
(3.27) |
Proudovou hustotu na levé straně můžeme vyjádřit pomocí proudu I tekoucího úzkou proudovou trubicí průřezu Δ S vedenou podél čáry l1 (viz obr. 3.5). Tento proud je podél celé proudové čáry konstantní, takže můžeme psát
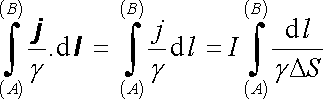 . . |
Veličina
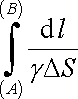 |
(3.20a) |
však podle (3.20) představuje odpor R příslušného úseku trubice, integrál
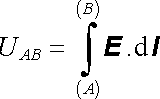 |
vyjadřuje příslušný pokles potenciálu. Dále zavedeme veličinu
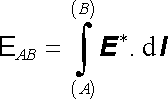 , , |
(3.28) |
kterou nazveme elektromotorickým napětím působícím na daném úseku proudové čáry. Dostaneme potom celkem
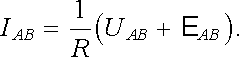 |
(3.29) |
Relace (3.29) vyjadřuje integrální tvar Ohmova zákona pro danou část nehomogenního vodiče. Říká, že proud tekoucí touto částí je úměrný součtu (elektrického) napětí a elektromotorického napětí, jež v ní působí.
Elektromotorické napětí je veličina, která má zřejmě stejný fyzikální rozměr jako potenciál. V Mezinárodní soustavě jednotek se proto měří rovněž ve voltech.
Proudové čáry stacionárního proudu jsou uzavřené křivky. Můžeme proto rozšířit integraci v (3.27) na celou (uzavřenou) čáru l1 (viz obr. 3.5). Dostaneme
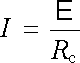 , , |
(3.30) |
přičemž Rc vyjadřuje celkový odpor proudové trubice a E > 0 vyjadřuje celkovou hodnotu elektromotorického napětí.
Vztah (3.30) říká, že proud tekoucí uzavřenou proudovou trubicí je přímo úměrný celkovému elektromotorickému napětí a nepřímo úměrný celkovému odporu trubice. V kapitole 7 poznáme některé konkrétní typy elektromotorických napětí. Uvidíme, že existují vtištěné síly nezávislé na čase. Vzhledem k tomuto faktu z rovnice (3.30) pak také vyplývá možnost existence stacio-nárního proudu ve vodiči. Výsledek (3.30) se někdy nazývá Ohmovým zákonem pro uzavřený obvod.
Uvažujme nyní speciální případ uzavřené proudové trubice, v níž působí vtištěná síla pouze na části li zatímco druhá část le je tvořena homogenním vodičem (viz obr. 3.6). Tento případ je důležitý z praktického hlediska, neboť modeluje tzv. elektrický obvod tvořený jednak homogenními pasivními vodiči (část le), jednak zdroji elektromotorického napětí, například galvanickými články (část li).
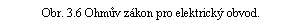
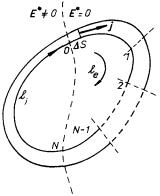
Vyšetříme nejdříve křivkový integrál (3.27) braný přes li. Po zavedení označení
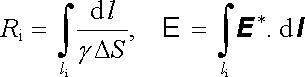 |
jej můžeme přepsat na tvar
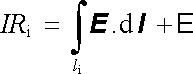 |
(3.31) |
ekvivalentní s (3.29) , který vyjadřuje závislost napětí mezi ekvipotenciálními plochami O, N na proudu. Představuje-li proudová trubice na obr. 3.6 model obvodu se zdrojem elektromotorického napětí, jsou řezy O, N svorkami tohoto zdroje. Rozdíl potenciálu mezi nimi je důležitou charakteristikou. Obvykle se zavádí pojem svorkového napětí vztahem
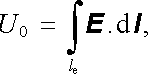 |
(3.32) |
které je vždy kladnou veličinou. Jelikož platí
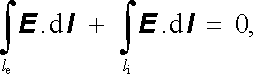 |
je možné místo (3.31) psát
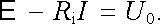 |
(3.33) |
Svorkové napětí je tedy vždy menší než elektromotorické napětí. Pouze ve speciálním případě nulového proudu platí mezi nimi rovnost. Rovnice (3.33) vyjadřuje prostou fyzikální situaci, která nastává ve zdroji elektromotorického napětí. Vtištěné síly, působící uvnitř zdroje, rozdělí volné nositele náboje tak, že mezi svorkami působí elektrické pole. V případě, kdy zdrojem neteče žádný proud, nastane rovnovážný (statický) stav při rovnosti elektromotorického a svorkového napětí. Za tohoto stavu platí podle (3.26) E = -E *, takže na nositele proudu uvnitř zdroje již další síly nepůsobí. Při odběru proudu jsou ze svorek zdroje odváděny náboje, čímž poklesne svorkové napětí i intenzita pole uvnitř zdroje. Působení vtištěných sil není pak zcela vykompenzováno a odvá-děné náboje mohou být neustále doplňovány.
Přejděme k vyšetření integrálu přes celou uzavřenou proudovou čáru (obr. 3.6). Integrál (3.27) lze upravit na tvar
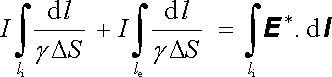 . . |
(3.34) |
Označíme-li ještě
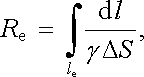 |
dostaneme
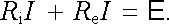 |
(3.35) |
Homogenní část proudové čáry le je možné rozdělit na libovolný počet částí body 1, 2, 3,..., N - l. Označíme-li
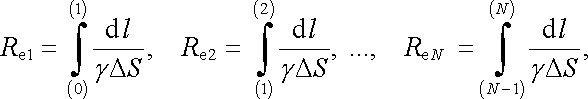 |
bude zřejmě platit
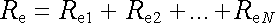 |
(3.36) |
a po dosazení do (3.35) získáme
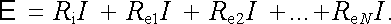 |
(3.37) |
Podle Ohmova
zákona pro homogenní vodiče
(3.19)
vyjadřuje každý člen
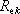 , k = 1,..., N, spád potenciálu v příslušné
části obvodu. Obsah výsledku
(3.37)
pak můžeme vyjádřit slovy: součet úbytků
napětí na všech odporech v obvodu působících je roven celkovému
elektromotorickému napětí E
.
, k = 1,..., N, spád potenciálu v příslušné
části obvodu. Obsah výsledku
(3.37)
pak můžeme vyjádřit slovy: součet úbytků
napětí na všech odporech v obvodu působících je roven celkovému
elektromotorickému napětí E
.
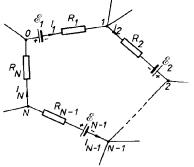
Uzavřenou
proudovou trubici podle obr. 3.6 považujeme za uzavřený elektrický obvod,
jestliže plášť trubice souhlasí s povrchem vodičů. Můžeme ji pak překreslit do
schematického tvaru podle obr. 3.7. Značkou
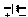 je - jak známo -
reprezentován zdroj elektromotorického napětí a jednotlivými značkami
je - jak známo -
reprezentován zdroj elektromotorického napětí a jednotlivými značkami
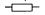 odpory jednotlivých úseků vodičů.
odpory jednotlivých úseků vodičů.
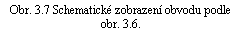
Tímto označením rozumíme dva poznatky, které jsou východiskem při řešení libovolně složitých elektrických obvodů.
I. Kichhoffovo pravidlo je důsledkem rovnice kontinuity proudu ve stacionárním přiblížení. Týká se celkového proudu vytékajícího ze styčného místa několika vodičů (tzv. uzlu).
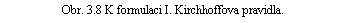
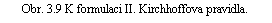
Uvažujme soustavu několika vodičů, které se stýkají ve společném uzlu (viz obr. 3.8) a které jsou obklopeny nevodivým prostředím. Označme postupně I1, I2,..., IN proudy tekoucí jednotlivými vodiči. Jestliže obklopíme uzel 0 libovolnou uzavřenou plochou S, bude celkový proud vytékající z této plochy zřejmě roven algebraickému součtu proudů tekoucích jednotlivými vodiči. Podle (3.16) pak dostaneme podmínku
 , , |
(3.38) |
která tvoří obsah I. Kirchhoffova pravidla: Celkový stacionární proud vytékající z libovolného uzlu je roven nule.
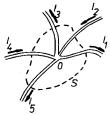
II. Kirchhoffovo pravidlo je důsledkem Ohmova zákona pro libovolnou smyčku vytvořenou z vodičů libovolně složitého elektrického obvodu. Příklad takové smyčky je uveden na obr. 3.9. Integrací Ohmova zákona (3.26) podél této smyčky vymezené body 0, l, 2,...,N, 0 bychom opět dostali vztah (3.37) , který můžeme zapsat ve tvaru
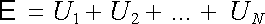 . . |
(3.39) |
Veličina E = E 1 + E 2 +...+ E N vyjadřuje celkové elektromotorické napětí působící ve smyčce a U1 = R1I1,...,UN = RN IN představují napětí v jednotlivých úsecích vodičů mezi sousedními uzly. Obsah vztahu (3.39) je opět možné vyjádřit slovy: Součet úbytků napětí na všech odporech ve smyčce působících je roven celkovému elektromotorickému napětí E působícímu ve smyčce.
Rozdělení integrační dráhy na jednotlivé úseky mezi sousedními uzly je v případě rozvětveného obvodu nutné, neboť každým úsekem teče obecně jiný proud. Výsledné elektromotorické napětí je rovno algebraickému součtu napětí všech zdrojů; při integraci může vyjít s kladným i záporným znaménkem, v závislosti na orientaci integrační dráhy. Rovněž napětí na jednotlivých odporech mohou vyjít kladná i záporná podle toho, jak je orientován směr integrace vůči skutečnému směru proudu. Volba směru integrace je ovšem lhostejná. Jeho změna odpovídá změně znaménka všech členů rovnice, odpovídá tedy násobení faktorem (-1).
Vlastnosti elektrických obvodů vyjádřené Kirchhoffovými pravidly jsou značně důležité z praktického hlediska. Pomocí nich a pomocí Ohmova zákona je možné vyřešit libovolně složitý stacionární obvod. To znamená, že pro dané zapojení obvodu, dané odpory vodičů a daná elektromotorická napětí všech zdrojů je možné pomocí Kirchhoffových pravidel a Ohmova zákona vypočítat proudy ve všech vodičích a potenciály všech uzlů. Některé příklady použití Kirchhoffových pravidel jsou uvedeny v článku 3.2.6, obecné metody řešení obvodů budou vyloženy v kapitole 8.
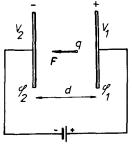
Nejdříve vyšetříme případ konvekčního proudu tvořeného proudem nabitých částic ve vakuu, v prostoru mezi elektrodami V1, V2 (viz obr. 3.10). Vnější zdroj nechť udržuje mezi elektrodami napětí U = φ 1 - φ 2. Částice nesoucí náboj q bude v prostoru mezi elektrodami vystavena působení síly F = qE. Při proběhnutí celé vzdálenosti d získá kinetickou energii W rovnou změně potenciální energie
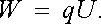 |
(3.40) |
Tato energie nemůže být elektrickému poli navrácena. Částice ji ztratí při nárazu na elektrodu. Energie se přitom promění v teplo, popřípadě v jinou formu energie v závislosti na konkrétní fyzikální situaci. Je proto zřejmé, že pro udržení proudu mezi elektrodami je nutné, aby elektrické pole dodávalo nositelům proudu energii.
Při průchodu proudu I bude za krátký časový interval Δ t dodána energie
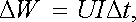 |
(3.41) |
takže výkon
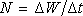 dodávaný zdroji elektrického pole bude dán
vztahem
dodávaný zdroji elektrického pole bude dán
vztahem
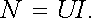 |
(3.42) |
Pro obecné úvahy je výhodnější najít diferenciální formu výrazu (3.42) . Za tím účelem uvažujme velmi malou část úzké proudové trubice vymezenou ekvipotenciálními ploškami Δ S1, Δ S2 (srov. obr. 3.4b). Vzdálenost plošek nechť je dána vektorem Δ I orientovaným ve směru spádu potenciálu. Pro jeho hodnotu Δ U bude platit Δ U = E .Δ I . Energie, kterou získá náboj Δ Q při proběhnutí vzdálenosti Δ l, bude rovna Δ Q(E .Δ I ). V čase Δ t, který potřebují nositelé proudu k proběhnutí vzdálenosti Δ l, projde potenciálovým rozdílem Δ U náboj Δ Q = (j .Δ S ) Δ t, jemuž předá pole energii
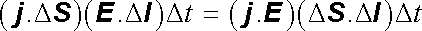 . . |
Veličina
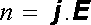 |
(3.43) |
tedy představuje hustotu výkonu předávaného elektrickým polem nositelům proudu. Vztah (3.43) reprezentuje hledané diferenciální vyjádření výrazu (3.42) .
Nyní přejdeme k vyšetřování kondukčního proudu ve vodiči. Uvažujme část vodiče vymezenou ekvipotenciálními plochami S1, S2 (obr. 3.4a), mezi nimiž je potenciálový spád U. Energii potřebnou k udržování proudu I v tomto vodiči určuje experimentálně nalezený Jouleův zákon, který říká: Ve vodiči protékaném proudem vzniká teplo (Jouleovo teplo). Tepelný výkon N vznikající ve vodiči protékaném proudem I, na němž je potenciálový spád U, určuje vztah
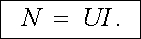 |
(3.44) |
Užitím Ohmova zákona můžeme (3.44) vyjádřit v jiném tvaru pomocí odporu vodiče R
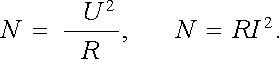 |
(3.45) |
Výrazy (3.44) , (3.45) vyjadřující Jouleův zákon lze také vyjádřit v diferenciálním tvaru pomocí měrné vodivosti γ , intenzity pole E , popř. hustoty proudu j . Jelikož vztahy (3.42) a (3.44) jsou formálně totožné, bude zřejmě i hledaný diferenciální tvar Jouleova zákona formálně totožný s výrazem (3.43)
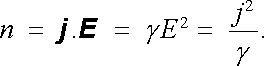 |
(3.46) |
Je však třeba si uvědomit, že přes tuto formální shodu popisují výrazy (3.42) a (3.43) na jedné straně a výrazy (3.44) a (3.46) na straně druhé zcela odlišné fyzikální situace. Nositelé konvekčního proudu se pohybují v prázdném prostoru. Jejich kinetická energie při přechodu od jedné elektrody ke druhé neustále vzrůstá. Práce spojitě dodávaná zdrojem elektrického pole je nositeli proudu akumulována a teprve při jejich nárazu na příslušnou elektrodu je měněna na teplo. Naproti tomu nositelé proudu ve vodiči jsou v neustálé interakci s látkou vodiče, jíž neustále předávají energii získanou od elektrického pole. Ke vzniku Jouleova tepla tedy dochází v celém objemu vodiče.
Ke konci článku vyšetříme ještě energetickou bilanci v uzavřeném elektrickém obvodu. Uvažujme obvod podle obr. 3.6. Platí pro něj rovnice (3.35) . Vynásobíme-li ji proudem I, dostaneme
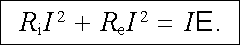 |
(3.47) |
Členy na levé straně vyjadřují podle (3.45) Jouleovo teplo vznikající jednak ve vnitřním odporu zdroje Ri, jednak v odporu vnějších vodičů Re. Předpokládáme-li, že v obvodu neprobíhají žádné další děje podílející se na energetické bilanci, je nutné vzhledem k zákonu zachování energie soudit, že člen na pravé straně vyjadřuje výkon Nz dodávaný zdrojem do obvodu
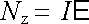 . . |
(3.48) |
Pro obecné úvahy je opět výhodné vztáhnout výkon dodávaný vtištěnými silami na jednotkový objem nehomogenního vodiče. Formuli vyjadřující tento výkon nz dostaneme zřejmě analogickým postupem jako výrazy (3.43) , resp. (3.46) . Bude tedy platit
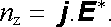 |
(3.49) |
Na základě právě uvedených úvah jsme dostali názorný obraz o fyzikální situaci v elektrickém obvodu. Do obvodu může být dodávána energie pouze prostřednictvím vtištěných (elektromotorických) sil, které konají práci. Tato práce vzniká na úkor jiné formy energie. (V galvanických článcích jde například o energii uvolňující se při chemických procesech.) Účinkem vtištěných sil se vytvoří elektrické pole, které předává energii nositelům proudu. Díky interakcím nositelů proudu s látkou vodiče je pohybová energie nositelů proudu předávána vodičům ve formě tepla.
Formální totožnost rovnic popisujících elektrostatické pole a elektrické stacionární pole se často využívá při řešení konkrétních úloh. Těžko řešitelnou úlohu o poli jednoho druhu je totiž v mnoha případech výhodné převést na úlohu o poli druhého druhu. Tuto situaci budeme demonstrovat na dvou příkladech.
V praxi se může vyskytnout úloha vyřešit průběh elektrostatického pole v okolí jisté soustavy elektrod udržovaných na konstantních potenciálech. Soustava může přitom být natolik složitá, že konkrétní průběh pole nelze vypočítat. V tomto případě je výhodné modelovat elektrostatické pole stacionárním a určit jeho průběh experimentálně. K modelování se zpravidla užívá tzv. elektrolytická vana. Modely elektrod se zhotoví z dobře vodivého materiálu a vloží se do kapaliny, jejíž vodivost je značně menší. Za těchto předpokladů lze povrch elektrod považovat za ekvipotenciální hladiny. V kapalině se vytvoří stacionární pole, jehož průběh odpovídá vyšetřovanému poli elektrostatickému. Rozložení potenciálu stacionárního pole v kapalině lze snadno vyšetřit experimentálně. Konkrétní způsob uspořádání je popsán například v [5].
Opačně může vzniknout potřeba vypočítat odpor homogenního vodiče obklopujícího danou soustavu elektrod. Přímý výpočet může být pro složitější uspořádání značně obtížný. Za předpokladu, že povrch elektrod lze považovat za ekvipotenciální hladiny, lze úlohu s výhodou převést na elektrostatický problém dané soustavy elektrod.
Jako příklad tohoto druhu vyšetříme dvojici elektrod V1, V2 zhotovených z velmi dobrého vodiče, jejichž geometrie odpovídá definici kondenzátoru (viz čl. 1.4.5), vnořených do "nekonečného" prostředí značně menší měrné vodivosti (viz obr. 3.11). Označíme-li φ 1 a φ 2 jejich potenciály, dostaneme podle Ohmova zákona vztah mezi proudem I protékajícím každou elektrodou a spádem poten-ciálu U = φ 1 - φ 2 . Tedy
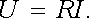 |

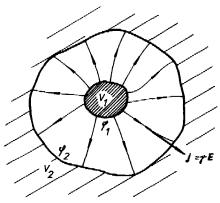
Odpor R působící mezi oběma elektrodami vypočítáme pomocí analogie s elektrostatickým polem. Nechť jsou nyní obě elektrody vnořeny do "nekonečného" měkkého dielektrika o permitivitě ε a nechť jsou na ně přivedeny náboje stejné velikostí Q, ale opačného znamení, které udržují původní hodnoty potenciálů. Vztah mezi velikostí náboje Q a spádem potenciálu pak lze vyjádřit pomocí kapacity C
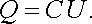 |
Náboj Q je však podle (1.276) dán tokem vektoru elektrické indukce přes povrch S kladně nabité elektrody, takže platí
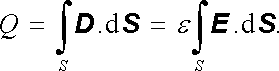 |
Na druhé straně lze proud I vyjádřit pomocí proudové hustoty
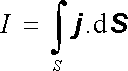 |
a podle Ohmova zákona
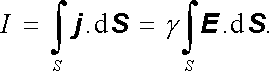 |
Spojením výrazů pro oba typy polí lze pak odpor R vyjádřit pomocí kapacity C
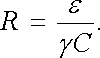 |
(3.50) |
Budeme-li tedy umět kapacitu vypočítat, popř. určit experimentálně, bude vyřešena i úloha o vedení proudu. Její výpočet může být ovšem obecně stejně obtížný jako výpočet odporu příslušného vodiče. Změřena však může být na kondenzátoru jen s danou geometrií elektrod a s libovolným vhodným dielektrikem.
Pomocí Ohmova zákona (3.19) a Kirchhoffových pravidel lze velmi snadno odvodit vztahy pro výpočet výsledného odporu několika vodičů zapojených sériově (obr. 3.12a), či paralelně (obr. 3.12b). Problém výsledného odporu několika sériově zapojených vodičů byl vlastně již řešen v čl. 3.2.3 (srov. obr. 3.6 a vztahy (3.35) až (3.37) ). Opakováním těchto úvah na odpory R1, R2,..., RN zapojené podle obr. 3.12a dostaneme pro výsledný odpor RS vztah analogický k (3.36)
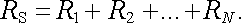 |
(3.51) |
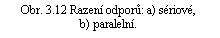
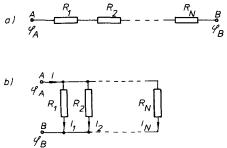
Při paralelním spojení podle obr. 3.12b je na všech odporech stejný spád potenciálu U = ℜ| φ A - φ Bℜ| a jednotlivé proudy I1, I2,..., IN jsou určeny Ohmovým zákonem
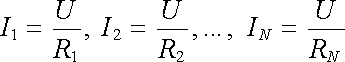 . . |
Výsledný proud I tekoucí body A, B je podle (3.38) roven součtu proudů prochá-zejících jednotlivými vodiči.
Po dosazení za tyto proudy a srovnáním výsledku s (3.19) dostaneme pro výsledný odpor RP paralelního spojení
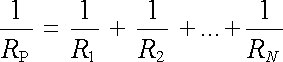 . . |
(3.52) |
Mějme tři prvky o odporech R1, R2, R3 zapojené do trojúhelníku a tři prvky o odporech RI, RII, RIII zapojené do hvězdy (obr. 3.13). Tato spojení bude možné v libovolném obvodu vzájemně zaměnit, budou-li výsledné odpory mezi body AB, AC, BC v obou uspořádáních stejné. Využitím vztahů (3.51) a (3.52) lze z uvedených požadavků získat rovnice, jejichž řešením jsou hledané transformační vztahy
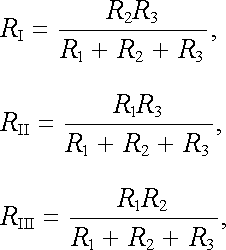 |
(3.53) |
respektive vztahy inverzní
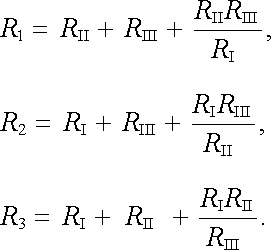 |
(3.54) |
Transformací hvězda-trojúhelník lze v některých případech zjednodušit řešení složitějších obvodů (srov. příklad 8.2.7c).
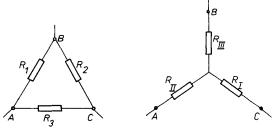
Obr. 3.13 Transformace hvězda trojúhelník.
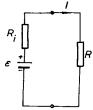
Je-li ke zdroji elektromotorického napětí E s vnitřním odporem Ri připojen spotřebič o odporu R (obr. 3.14), je výkon dodávaný zdrojem do spotřebiče závislý na vzájemném vztahu odporů R a Ri Bude-li odpor R příliš velký, poteče jím malý proud a výkon dodaný do spotřebiče bude malý. Naopak bude-li odpor R příliš malý, bude proud v obvodu určen vnitřním odporem zdroje a výkon dodaný do spotřebiče bude rovněž malý. Optimální hodnota výkonu dodaného do spotřebiče je dána maximem funkce
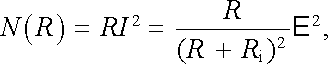 |
které nastává při splnění podmínky
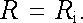 |
(3.55) |
O tomto stavu říkáme, že spotřebič je výkonově přizpůsoben zdroji.
E