---

---

3.1 Elektrický proud

3.1.1 Pojem elektrického proudu, hustota proudu

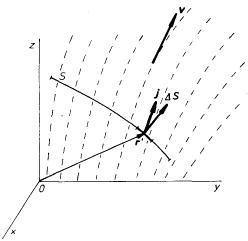
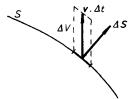
Samotné přemisťování elektrického náboje nazýváme elektrickým proudem. Pro jeho kvantitativní zavedení předpokládejme (jako dosud vždy), že pozorování provádíme v určité inerciální soustavě, v níž je dána pevná orientovaná plocha S (viz obr. 3.1).[15] Můžeme si představit, že v prostoru dochází k pohybu nositelů náboje, z nichž některé prochází uvažovanou plochou S. Projde-li v časovém intervalu Δ t touto plochou v kladném směru náboj Δ Q, definujeme veličinu

,

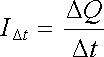(3.1)

kterou nazýváme průměrným proudem. Limitní hodnotu

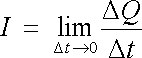(3.2)

označíme jako okamžitý proud (nebo krátce proud) tekoucí plochou S.

Obecně je třeba považovat proud za funkci času. Je-li proud skutečně s časem proměnný, mluvíme o nestacionárním proudu, proud časově neproměnný nazý­váme proudem stacionárním. Množství náboje Q, které proteče danou plochou v konečném časovém intervalu (0, t), je zřejmě dáno vztahem

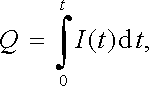(3.3)

který se v případě stacionárního proudu redukuje na prostý součin

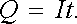(3.4)

Proud je zřejmě skalární veličina, která může nabývat kladných i záporných hodnot. Kladný je tehdy, protéká-li v kladném směru kladný náboj. Jestliže při­tom vytéká z jednoho objemu a vtéká do druhého, znamená pravá strana (3.1) , popř. (3.2) , přírůstek náboje za jednotku času v objemu, kam náboj vtéká, nebo úbytek náboje za jednotku času v objemu, z něhož náboj vytéká. Průchod kladného náboje jedním směrem je ekvivalentní průchodu záporného náboje opačným směrem.

Přejdeme k definici hustoty proudu. Hustotou proudu rozumíme vektorovou veličinu j (r ) definovanou v každém bodě plochy S protékané proudem, která popisuje rozložení proudu na této ploše. Proud I_i tekoucí libovolnou částí S_i plo­chy S lze pak vyjádřit vztahem

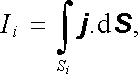(3.5)

který můžeme považovat za integrální definiční rovnici hustoty proudu (srov. analogický postup při zavádění pojmu hustoty náboje v článku 1.1.4). Z význa-mu hustoty proudu vyplývá, že proud Δ I tekoucí velmi malou ploškou Δ S tvořící část plochy S, bude možné přibližně vyjádřit vztahem (viz obr. 3.1)

,

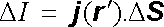(3.6)

ve kterém r ℜ' představuje libovolný bod plošky Δ S . Ve speciálním případě, kdy je proud rovnoměrně rozdělen po celé ploše rovinné S , tj. v případě, kdy má proudová hustota ve všech bodech plochy stejnou velikost a směr, redukuje se integrál (3.5) na prostý součin

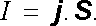(3.7)

Hustota proudu reprezentuje nové vektorové pole. Z toho, co o ní bylo dosud řečeno, je zřejmé, že její orientace udává v daném bodě kladný směr proudu a její velikost vyjadřuje velikost proudu připadající na jednotku plochy. Hustota stacionárního proudu zřejmě nezávisí na čase, zatímco hustota nestacionárního proudu je explicitní funkcí času.

Pro popis rozložení proudu ve vodiči je výhodné zavést pojmy analogické těm, které se užívají pro popis rozložení elektrostatického pole. Proudovou ča­rou rozumíme křivku, jejíž tečny mají vždy směr hustoty proudu. Proudovou trubicí rozumíme část prostoru (z vnějšku) vymezenou plochou tvořenou prou­dovými čarami. Touto plochou, která tvoří plášť trubice, tedy neprotéká žádný proud. Hustotu proudu chápeme v celé této knize (s výjimkou oddílu 5.4) jako makroskopickou veličinu, která nebere zřetel na diskrétní mikrofyzikální struk­turu náboje. V tomto ohledu je zcela analogická hustotě náboje, se kterou jsme pracovali v kapitole l.

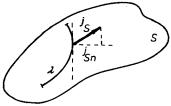
Dosud jsme proud považovali za prostorovou záležitost a chápali jsme jej jako přemisťování objemově rozložených nábojů. Analogicky však můžeme hovořit také o plošných proudech, kterými rozumíme pohyb plošných nábojů po povrchu určitých těles. Nechť je dáno určité těleso, na jehož povrchu S je rozlo­žen plošný náboj, který se po tomto povrchu může pohybovat. Pak můžeme zavést pojem plošného proudu I_S, tekoucího libovolnou křivkou λ , ležící na ploše S (viz obr. 3.2).

Označíme-li Δ Q náboj, který projde křivkou λ ve zvoleném směru za časový interval Δ t, máme analogicky k (3.2)

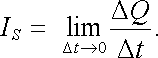(3.2a)

Můžeme také zavést hustotu plošného proudu j _S, (srov. čl. 1.1.4). Analogicky k  (3.5) bude platit

.

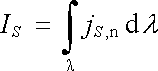(3.5a)

Pojem plošného proudu je užitečný při vyšetřování magnetického pole v látkách (viz oddíl 3.5).

Jednotkou proudu v Mezinárodní soustavě jednotek je ampér (A), který je v této soustavě základní jednotkou a je definován pomocí magnetických účinků proudu (viz čl. 3.3.2, popř. Dodatek 2). Vztah mezi ampérem a jednotkou náboje coulombem je dán výrazem (3.2) , respektive (3.3) . Jeden coulomb je takové množství náboje, které proteče danou plochou za jednu sekundu, jestliže touto plochou teče proud jednoho ampéru. Jednotkou hustoty objemového proudu je podle (3.5) až (3.7) ampér na metr čtverečný (A.m^-2). Analogicky jednotkou hustoty plošného proudu je ampér na metr (A.m^-1).

3.1.2 Mechanismy vedení proudu

Přemisťování náboje v prostoru může být uskutečňováno několika způsoby. Podle charakteru přemisťování náboje rozlišujeme několik typů proudu. Přede­vším může jít o volné proudy, které vznikají při přemisťování volných nábojů na makroskopické vzdálenosti. Volné proudy mohou být realizovány buď pohybem volných nositelů náboje v látkovém prostředí (tj. ve vodičích), nebo makrosko­pickým pohybem volných nositelů náboje v prázdném prostoru. V prvním pří­padě mluvíme o proudech kondukčních, ve druhém případě o proudech kon­vekčních.

Konkrétní fyzikální zákonitosti platné pro kondukční proudy budou diskuto­vány v kapitole 7. Bude například ukázáno, že zatímco v pevných látkách je elektrický proud realizován především elektrony, v kapalinách jsou standardními nositeli proudu ionty a průchod proudu je doprovázen transportem hmoty.

V kapitole o elektrostatice jsme viděli, že při změně polarizace dielektrika může docházet ke změnám v prostorovém rozložení makroskopických vázaných nábojů, při nichž nedochází k pohybu žádných nositelů náboje na makrosko­pické vzdálenosti. Změny v prostorovém rozložení makroskopických vázaných nábojů jsou tedy působeny zásadně odlišným pohybem nositelů náboje než v případě volných proudů. Mluvíme o polarizačním proudu v dielektriku, který je jedním typem tzv. vázaných proudů. [16]

V případě volných proudů existuje jednoduchý vztah mezi hustotou proudu, hustotou náboje a rychlostí pohybu. Nechť jsou v daném místě prostoru rozlo­ženy kladné náboje s objemovou hustotou ρ ₊ a záporné náboje s hustotou ρ _-. Nechť dále v ₊ je rychlost kladných a v _- rychlost záporných nábojů. Množství kladného náboje Δ Q₊, které projde malou ploškou Δ S za krátký časový interval Δ t, vyplní zřejmě objem Δ V (viz obr. 3.3), takže platí Δ Q₊ = ρ ₊Δ V = ρ ₊( Δ S .v ₊ )Δ t. Hustota proudu j ₊ tvořeného kladnými náboji je tedy dána vzta­hem

.

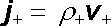(3.8)

Pro hustotu proudu vytvořeného zápornými náboji platí analogicky

.

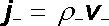(3.9)

Celková hustota kondukčního proudu v daném bodě je pak dána vektorovým součtem obou příspěvků

.

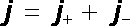(3.10)

V praxi nastává často případ, že vodič je jako celek elektricky neutrální, takže platí ℜ| ρ ₊ℜ|  = ℜ| ρ _-ℜ| . Potom lze celkovou proudovou hustotu j zřejmě vyjád­řit ve tvaru

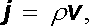(3.11)

kde 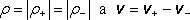je relativní rychlost obou typů nositelů.

Vztahy analogické k (3.8) až (3.11) lze zřejmě získat i pro případ plošných proudů. V těchto jednotlivých vztazích je třeba pouze nahradit proudovou hus­totu j hustotou plošného proudu j _S a hustoty objemového rozložení náboje pří­slušnými plošnými hustotami.

V případě polarizačního proudu v dielektriku lze hustotu proudu jednoduše vyjádřit pomocí časové změny vektoru polarizace. Uvažujme za tímto účelem libovolnou uzavřenou plochu S uvnitř dielektrika a označme Q_P celkový vázaný náboj v ní obsažený. Celkový polarizační proud I_P tekoucí plochou S lze podle (3.5) vyjádřit pomocí hustoty j _P ve tvaru

.

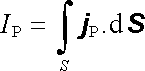Na druhé straně je proud I_P dán úbytkem náboje Q_P za jednotku času, I_P = -  dQ_P/dt. V případě, že uvnitř plochy jsou vázané náboje jen objemově rozložené, můžeme podle čl. 1.5.2 psát

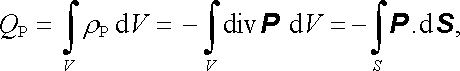což znamená

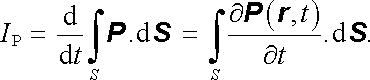Spojením obou vyjádření dostáváme pro hustotu polarizačního (posuvného) proudu j _P

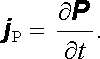(3.12)

Všechny tři uvedené mechanismy, které reprezentují pohyb reálných nábojů, mohou obecně přispívat k výslednému proudu. Celkový proud tekoucí v pro-storu je pak superpozicí příspěvků všech těchto mechanismů. Hustota posuvného proudu nemůže však být časově nezávislá, poněvadž polarizace dielektrika nemůže do nekonečna vzrůstat ani klesat. Posuvný proud proto nemůže přispívat ke stacionárnímu proudu, který je tudíž vždy dán jen proudy volnými.

3.1.3 Rovnice kontinuity proudu

Tato rovnice je matematickým vyjádřením zákona zachování náboje. Jak bylo vyloženo v předchozích kapitolách, vyjadřuje zákon zachování náboje experi­mentálně ověřený poznatek (platný v makroskopickém i mikroskopickém mě­řítku), že náboj nikde nevzniká ani nezaniká.

Uvažujme libovolnou uzavřenou plochu S, která tvoří povrch tělesa objemu V. Předpokládejme, že z této plochy vytéká proud I, takže za krátký časový in­terval Δ t z ní vyteče náboj Δ Q ℜ' , o který se vzhledem k zákonu o zachování ná­boje musí zmenšit celkový náboj uzavřený v ploše. Označíme-li tento úbytek - Δ Q, dostaneme -Δ Q = IΔ t, odkud plyne pro limitní případ Δ  t ℜ →  0 podmínka

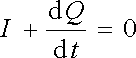(3.13)

nazývaná rovnice kontinuity proudu v integrálním tvaru, v níž Q = Q(t) repre­zentuje okamžité množství náboje uzavřeného v ploše S.

Rovnice (3.13) je přímým důsledkem zákona zachování náboje, a platí tudíž zcela obecně. Vyloučíme-li z úvah plošné náboje a plošné proudy, můžeme zís­kat její matematicky konkrétnější tvar. Především lze vztahem typu (3.5) vyjád­řit proud I pomocí hustoty proudu

.

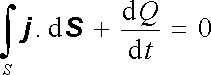(3.14)

Dále můžeme náboj Q vyjádřit jako objemový integrál hustoty náboje ρ  = ρ (r , t). Předpokládáme-li, že poloha a tvar plochy S nezávisí na čase, můžeme psát

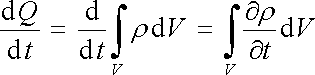a levou stranu (3.14) upravit známým způsobem pomocí Gaussovy věty. Dosta­neme diferenciální tvar rovnice kontinuity

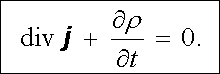(3.15)

Ve speciálním případě stacionárního proudu musí být člen dQ/d t, pop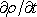ř. ve vztazích (3.13) a (3.14) , a tedy i v (3.15) roven nule. Z libovolné uzavřené plochy nemůže totiž vytékat od nuly různý stacionární (tj. časově nezávislý) proud, neboť by v objemu jí ohraničeném musel existovat buď zdroj nekonečně velkého náboje, nebo by se v něm musel nekonečně velký náboj ztrácet. Pro stacionární proud má tedy rovnice kontinuity tvar

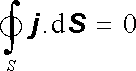(3.16)

nebo

.

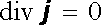(3.17)

Zákon zachování náboje se vztahuje na všechny náboje uzavřené v uvažované ploše S. Bylo by proto přirozené proud I a náboj Q v (3.13) chápat jako celkový proud vytékající z plochy S a jako celkový náboj v ní obsažený. Podobně v diferenciálním tvaru (3.15) by vystupovala celková hustota proudu j a celková hustota náboje ρ v daném bodě. Častěji se však rovnice kontinuity formuluje pro volné proudy, které mají větší praktický význam. Symboly v  (3.13) a (3.15) mají pak význam příslušných veličin volného proudu v dané soustavě. Platnost rovnice kontinuity v tomto obvyklém tvaru je ovšem vázána na podmínku, která je v praxi často splněna, a to že se v dané soustavě zachovává charakter nositelů náboje, tj. že se například počet volných nositelů náboje nemění na úkor počtu nositelů náboje vázaného.

 

 

---

---