Elektronické obvody při velmi vysokých frekvencích

Mnohé z problémů, které v elektronice studujeme, zahrnují elektrické obvody. Pod tímto pojmem si intuitivně představujeme něco, co je v elektronické praxi důležité a souvisí s teorií elektromagnetického pole. V úloze s obvodem je často přiložené napětí, existují proudy ve vodičích obvodu, náboje na kondenzátorech v obvodu, ohmické ztráty a eventuelně i ztráty výkonu vyzařováním. Na obvodech lze také jednoduše demonstrovat souvislost příčiny a následku (změním odpor, změní se proud). Budeme se proto snažit zkoumat elektrické obvody z hlediska základních zákonů elektrodynamiky. Pro obvody malé (rozměry) ve srovnání s vlnovou délkou odpovídající kmitočtu, se kterou obvod pracuje, najdeme, že tento exaktní přístup vede přímo ke známým přístupům řešení obvodů na základě Kirchhoffových zákonů a představa soustředných parametrů je pro analýzu obvodů dostatečná. V praxi se však často používá obvodů při tak vysokých kmitočtech, že uvedená podmínka není splnitelná. Proto je třeba pojem obvodu rozšířit i na případ, kdy předpoklad „soustředěnosti“ parametrů není splněn. Další důvody pro rozšíření této představy jsou následující:

(1) Široké použití vysokých kmitočtů v řadě obvodů bez dostatečného porozumění zvyšuje nejistotu při návrhu a vývoji obvodů a tím se doba jejich návrhu prodlužuje. Např. intuitivně přistupujeme k řešení vysokofrekvenčních obvodů na základě studia systémů, kde proud teče skrze relativně malý průřez vodiče. Je zřejmé, že to je jen určitý speciální případ obecnějšího problému, kdy proud teče - je rozložen - do velké oblasti prostoru. Na druhé straně by bylo výhodné i pro obvody tohoto typu použít užitečné (a jednoduché) metody řešení známé z obvodů se soustředěnými parametry.

(2) Uvažujeme-li vyzařování - radiaci - energie, musíme studovat jednak vlastní mechanizmus uvolňování energie z obvodu - antény, jednak transport energie do místa, kde se vyzařuje - přenosové vedení.

Při tom všem je snaha využít známých přístupů - pojmů přiložené napětí, impedance, atd. Pokusíme se tedy dát dohromady kombinaci přístupů obvodových a teoretických.

I. Kirchhoffův zákon

V klasické teorii obvodů definujeme nejdříve větev obvodu jako aktivní (zdroj) nebo pasivní (R,L,C) dvojpól a pak uzel jako místo, kde se stýkají alespoň dvě větve. Stýká-li se v uzlu N větví (N≥2) pak podle I. Kirchhoffova zákona platí:

 (algebraická suma proudů do uzlu vtékajících se v každém časovém okamžiku rovná nule).

Je zřejmé, že teoretická idea za tímto zákonem skrytá, tkví v rovnici kontinuity:

        (1.5.1)

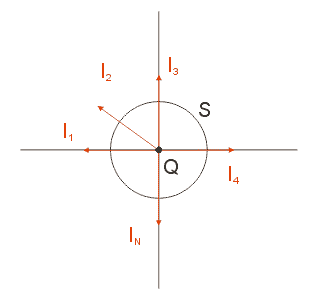Představíme-li si nyní plochu S tak, že obepíná uzel Q a procházejí jí všechny do uzlu vcházející vodiče, bude na levé straně rovnice (1.5.1) prostý součet proudů soustředěných do vodičů vtékajících do uzlu (s příslušnými znaménky) a na pravé straně časová změna náboje Q, pokud se nějaký v uzlu akumuluje.  Takže (1.5.1) může být zapsáno jako               (1.5.2), což je ve zjevném rozporu s původním zápisem. Tento rozpor je jen zdánlivý, neboť při praktické aplikaci Kirchhoffova zákona přidáváme novou větev, větev s kapacitou,  je proud nabíjející (vybíjející) tuto kapacitu. Pak N přejde na N+1 a když   -   převedeme na levou stranu rovnice, dostaneme zápis totožný s původním.

Obr.1.4.1 Plocha S obepínající uzel Q

Úloha:

Ukažte, že člen na pravé straně rovnice (1.5.2) je posuvný proud, který teče ven s plochy S.

Rozdíl mezi rovnicí (1.5.2) a klasickým zápisem je tedy jen formální. Rovnice (1.5.2) je názornější a klasický zápis je častější. Připomeňme, že jsme při odvozování rovnice (1.5.2) předpokládali, že proudy tečou jen ve vodičích. Nediskutovali jsme zatím případ velmi vysokých kmitočtů.

Vztah pole a proudu (Ohmův zákon)

Snad nejjednodušší a asi i nejdůležitější vztah, který se používá v klasické teorii obvodů je Ohmův zákon. Dává do souvislosti proud a napětí na vodiči, kterým tento proud prochází. V diferenciálním tvaru zní: .

Je to vztah pro hustotu proudu v určitém bodě vodiče za předpokladu, že známe celkovou intenzitu elektrického pole  v tomto bodě. Zde zdůrazňujeme pojem celková, neboť ve skutečném obvodu se skládá vtištěné pole ze zdroje energie s poli vznikajícími v obvodu díky změnám proudu a náboje v systému. Změny proudu v obvodu vyvolávají změny napětí na kapacitách a indukčnostech obvodu. Jen část původního pole zůstává na ohmické úbytky.

Celkové pole  je složeno ze dvou základních částí:

_o + , kde _o je vtištěné pole z externího generátoru (zdroje) a  vzniká změnami nábojů a proudů ve vlastním obvodu.

Pokud bychom tento obvod řešili z hlediska Maxwellových rovnic, byl by to jeden systém, kde by na sebe vzájemně působily generátor energie (zdroj) a proudy tekoucí v „pasivní“ části obvodu. Toto ovlivňování skutečně v praxi nastává a např. odražený výkon může způsobit vážné poškození generátoru, pokud tento nemá příslušnou ochranu. Často lze předpokládat, že zdroj a zbytek obvodu jsou nezávislé, čímž se analýza obvodů zjednoduší. V praxi se např. jedná o obvod, kdy zátěž je dobře přizpůsobena, takže k ovlivnění generátoru odraženým výkonem nedochází. Pak můžeme _o považovat za nezávislé na nábojích a proudech v obvodu a z druhé strany závisí pouze na změnách nábojů a proudů v obvodu. Proto aplikujeme základní rovnice jen na toto indukované pole. Předpokládáme-li, že je dáno vtištění pole _o, platí  .

Indukované pole  se dá vyjádřit pomocí skalárního a vektorového potenciálu:    

Z Maxwellových rovnic  lze vyjádřit: .

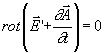Kde    je nevírové pole a dá se tedy napsat jako gradient skalární funkce .

Použitím Gaussovy věty  dostaneme:

          (1.5.3) 

Aplikujeme Faradayův zákon elektromagnetické indukce  , neboli

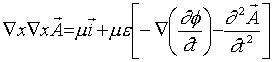
(Na rozepsání  použijeme vzorec ⇒  ) a dostaneme:

    (1.5.4).

Vektorový potenciál není rovnicí  definován jednoznačně a můžeme k němu přidat libovolný gradient skalární funkce - kalibrační podmínku. Tu obvykle nepíšeme ve tvaru přímo pro , ale pro . Nejjednodušší je  . 

Zde ale použijeme Lorentzovu kalibrační podmínku, která pro nevodivé prostředí (vodivostní část máme v naší úvaze zvlášť) zní: ,  čímž z rovnice (1.5.4) vymizí zbytečné členy a dostaneme nehomogenní vlnovou rovnici pro  ( podobně z rovnice (1.5.3)  nehomogenní vlnovou rovnici pro φ):

 neboli       ;     

Z těchto vlnových rovnic plyne, že při změně rozložení náboje (proudu), změní se potenciály až za dobu , kde  . Jedná se o tzv. retardované potenciály.

Vraťme se však k našemu problému.

Můžeme napsat, že  neboli     (1.5.5).

To je vztah typu příčina a důsledek, neboť vtištěné pole  má za následek člen ohmický a členy způsobené náboji a proudy v obvodu. To je první krok při postupu k odvození obvodových vztahů, který přitom vychází z rigorózní teorie. Nyní musíme přesně definovat, co míníme obvodem, abychom mohli vztah (1.5.5), který platí v určitém místě ve vodiči převést na integrální tvar platící pro smyčku neboli obvod.

II. Kirchhoffův zákon

Předpokládejme nejprve stejnosměrný případ:

Napětí baterie působí proud a to je to jediné, co proud působí, neboť nemáme žádné proměnné proudy ani žádná elektrická pole ve vodivé smyčce způsobené náboji (pomíjíme přechodný efekt zapnutí; jakmile se proud ustaví a eventuelně parazitní kapacity nabijí, neovlivňují nijak výsledný proud). Teorie obvodů říká, že baterie musí vytvořit elektrické pole ve vodiči, neboť jinak (při ) by netekl žádný proud . Tím, že jsme definovali napětí rovnicí (1.5.7), jsme oba náhledy spojili. Přesto ani teorie obvodů, ani teorie pole se nestará o to, jakým způsobem napětí, resp. pole vzniklo. Ze zkušenosti víme, že napětí na svorkách baterie nezáleží na orientaci baterie v prostoru, jinak řečeno ať povedeme integrál (1.5.7) po libovolné křivce spojující svorky, bude napětí stále stejné. Pokud však máme co dělat s obvody pracujícími s časově proměnnými proudy a napětími, musíme se smířit s tím, že zdrojem může být např. anténa přijímající signál od vzdáleného vysílače, a pak velmi záleží na tom, jak je tato anténa orientována v prostoru, neboli jakou křivku zvolíme pro integrál (1.5.7). Nyní již můžeme rovnici (1.5.6) interpretovat jako II. Kirchhoffův zákon - přiložené napětí se rovná součtu úbytků podél obvodu (nejenom ohmických). Tyto úbytky jsou definovány v rovnici (1.5.6) na pravé straně a interpretujeme je:

. . . . ohmický úbytek, . . . . . . . “induktivní“ úbytek, . . . “kapacitní“ úbytek. 

(Rozmyslete si, proč tento integrál není obecně roven 0; co způsobuje jeho „nenulovost“ ?). 

Nejlépe se interpretují tyto členy pro „pomalé“ změny  a  -  v obvodech se soustředěnými parametry můžeme integrovat u příslušného členu jenom od jedné svorky např. cívky ke druhé, neboť příspěvek dalších částí obvodu k tomuto „úbytku „ je zanedbatelný. Se vzrůstajícím kmitočtem hranice mezi původně „soustředěnými“ elementy obvodu mizí a proto pro obvody velmi vysokých kmitočtů nemá aplikace II. Kirchhoffova zákona praktický smysl.

<<< předchozí | hlavní stránka | další >>>