Elektrické pole
Intenzitu elektrického pole definujeme jako sílu působící na jednotkový náboj:
![]()
![]()
V látkovém prostředí definujeme vektor elektrické indukce
![]() ;
kde
;
kde ![]() je vektor
elektrické polarizace (elektrický dipólový moment jednotky objemu). Obvykle
se předpokládá lineární závislost
je vektor
elektrické polarizace (elektrický dipólový moment jednotky objemu). Obvykle
se předpokládá lineární závislost
![]() ; kde χ
je elektrická susceptibilita. Z toho
; kde χ
je elektrická susceptibilita. Z toho
![]() , kde
, kde
![]() .
.
Zdrojem toku elektrické indukce je náboj - elektrické pole je zřídlové. Platí Gaussova věta: Tok vektoru elektrické indukce uzavřenou plochou obklopující náboj q je úměrný množství náboje a nezávisí na tvaru plochy:
![]() neboli
neboli
![]()
Ze zkušenosti plyne, že v elektrostatickém poli nezávisí práce, kterou vykoná náboj q po křivce, na tvaru křivky, neboli že pohybem po libovolné uzavřené křivce práci nekonáme:
![]() neboli
neboli
![]() . Z toho plyne, že
. Z toho plyne, že
![]() lze napsat jako
-grad φ. Pro φ platí
Laplaceova -Poissonova rovnice
lze napsat jako
-grad φ. Pro φ platí
Laplaceova -Poissonova rovnice
![]() .
.
Energie elektrostatického pole: Práce vykonaná přemístěním
bodového náboje q´ z ∞ do vzdálenosti r od bodového náboje q
je rovna
![]() . Pro velké množství nábojů se tyto práce sčítají:
. Pro velké množství nábojů se tyto práce sčítají:
![]() (ve
vzorci je
(ve
vzorci je ![]() ,
abychom každý příspěvek nepočítali dvakrát).
,
abychom každý příspěvek nepočítali dvakrát).
Potenciál v místě j-tého náboje je
![]() a tedy
a tedy
![]() ; za
ρ dosadíme z Gaussovy věty div
; za
ρ dosadíme z Gaussovy věty div
![]() a použijeme
identity:
a použijeme
identity:
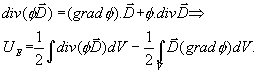
Použijeme Gaussovu větu na první integrál:
![]() a bereme plochu v ∞ a
první integrál je 0 a
a bereme plochu v ∞ a
první integrál je 0 a
![]() ;
objemová hustota
energie je
;
objemová hustota
energie je ![]() .
.
Zákon zachování náboje; plyne ze zkušenosti a experimentu; z něj plyne rovnice kontinuity (platí vždy):
![]()
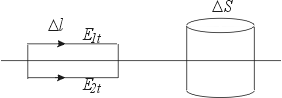
Obr.1.3.1 Tečné složky na rozhraní dvou prostředí
Tečné složky:
![]() ze vztahu
ze vztahu
![]()
neboli
![]() .
.
Normálové složky:
![]() z Gaussovy věty
z Gaussovy věty
![]() neboli
neboli
![]()
Magnetické pole
Magnetickou indukci definujeme pomocí silových účinků na
pohybující se náboj:
![]() , kde
, kde
![]() je rychlost náboje.
Vektor magnetické intenzity definujeme jako
je rychlost náboje.
Vektor magnetické intenzity definujeme jako
![]() je vektor
magnetizace (magnetický dipólový moment jednotky objemu látky), obvykle se
předpokládá
je vektor
magnetizace (magnetický dipólový moment jednotky objemu látky), obvykle se
předpokládá
![]() ; kde χ
je magnetická susceptibilita,
; kde χ
je magnetická susceptibilita,
![]() , kde
, kde
![]() .
.
Z experimentů plyne, že magnetický indukční tok libovolnou
uzavřenou plochou je vždy roven nule:
![]() , tj. neexistuje magnetický náboj,
, tj. neexistuje magnetický náboj,
![]()
Ve statickém magnetickém poli je křivkový integrál
magnetické intenzity
![]() podél uzavřené
křivky ohraničující proud I úměrný velikosti tohoto proudu:
podél uzavřené
křivky ohraničující proud I úměrný velikosti tohoto proudu:
![]() (Ampérův zákon) neboli rot
(Ampérův zákon) neboli rot
![]() .
.
Z rovnice
![]() plyne, že
plyne, že
![]() lze
napsat jako
lze
napsat jako
![]() , kde
, kde
![]() je definováno až na
gradient φ
kalibrační podmínka např.
je definováno až na
gradient φ
kalibrační podmínka např.
![]() . Pak
. Pak
![]() (homogenní prostředí).
(homogenní prostředí).
Energie magnetostatického pole:
výraz
![]() je možné
interpretovat jako interakční energii částice s vnějším magnetickým polem.
Pro náboje s hustotou r:
je možné
interpretovat jako interakční energii částice s vnějším magnetickým polem.
Pro náboje s hustotou r:
![]() ,
kde
,
kde ![]() .
Pak
.
Pak ![]() .
.
To je interakční
energie proudu
![]() v daném poli
v daném poli
![]() .
.
![]() (je-li pole vytvořeno týmiž proudy
(je-li pole vytvořeno týmiž proudy
![]() , je třeba dělit výraz 2, abychom
interval energií
proudových elementů nezapočítali dvakrát)
, je třeba dělit výraz 2, abychom
interval energií
proudových elementů nezapočítali dvakrát)
Veličinu
![]() interpretujeme jako
práci potřebnou na vytvoření magnetického pole.
interpretujeme jako
práci potřebnou na vytvoření magnetického pole.
Upravíme:
![]()
![]()
![]() , jsou-li proudy soustředěny v konečné
oblasti
, jsou-li proudy soustředěny v konečné
oblasti
![]() a objemová hustota
energie je
a objemová hustota
energie je
![]() .
.
Na rozhraní dvou prostředí (z obdobné úvahy jako pro
elektrostatiku a použitím vztahů
![]() a
a
![]() ):
):
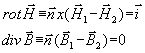
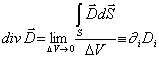 (Einsteinova sumační
konvence)
(Einsteinova sumační
konvence) 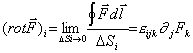 (εijk - Levi - Civitův symbol)
(εijk - Levi - Civitův symbol)