Stejnosměrné a nízkofrekvenční obvody
-
Pro stejnosměrné proudy platí
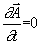 a obvodem neteče proud, pokud nebude úplně uzavřen. Integrály
a obvodem neteče proud, pokud nebude úplně uzavřen. Integrály
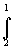 ... jsou
integrály křivkové podél uzavřené křivky:
... jsou
integrály křivkové podél uzavřené křivky:
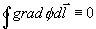 , protože φ
je prostý skalár nezávislý na čase. Proudovou hustotu
, protože φ
je prostý skalár nezávislý na čase. Proudovou hustotu
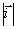 vypočítáme z celkového protékajícího proudu:
vypočítáme z celkového protékajícího proudu:
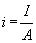 , kde
A je plocha průřezu vodiče. Pak
, kde
A je plocha průřezu vodiče. Pak
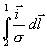 =
=
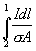 (
I a dl mají stejný směr)
⇒ I
(
I a dl mají stejný směr)
⇒ I
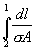 (A
přitom může být funkcí I).
Integrál u I
se nazývá stejnosměrný odpor R dráhy 21 a platí integrální Ohmův zákon
(A
přitom může být funkcí I).
Integrál u I
se nazývá stejnosměrný odpor R dráhy 21 a platí integrální Ohmův zákon
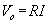 .
.
-
Nízkofrekvenčními obvody míníme takové obvody, které
nebo
Ze zkušenosti víme a později si ukážeme, že střídavé proudy nejsou rozloženy ve vodiči rovnoměrně, ale že preferují povrch vodiče
- skin efekt. Pro proudovou hustotu
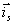 při povrchu vodiče musí
také platit Ohmův zákon:
při povrchu vodiče musí
také platit Ohmův zákon:
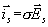 .
.
Představíme-li si integrační křivku blízko povrchu vodiče, můžeme psát
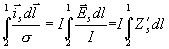 , kde
, kde
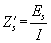 je
vnitřní impedance příslušného vodiče.
je
vnitřní impedance příslušného vodiče.
Rozložení proudu při povrchu vodiče je závislé na kmitočtu.
Pro definici
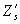 musíme předpokládat harmonické časové změny
jedné frekvence.
Povrchové elektrické pole
musíme předpokládat harmonické časové změny
jedné frekvence.
Povrchové elektrické pole
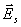 není ve fázi s proudem.
není ve fázi s proudem.
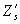 má reálnou složku a imaginární složku.
Reálná složka představuje střídavý odpor a imaginární vnitřní
reaktanci. Vnitřní reaktance vzniká z magnetického toku uvnitř vodiče.
Někdy se též nazývá vnitřní indukčnost a značí se Li.
má reálnou složku a imaginární složku.
Reálná složka představuje střídavý odpor a imaginární vnitřní
reaktanci. Vnitřní reaktance vzniká z magnetického toku uvnitř vodiče.
Někdy se též nazývá vnitřní indukčnost a značí se Li.
Pro induktivní
člen a střídavý nízkofrekvenční
případ
(naše předpoklady platí do frekvencí řádu jednotek GHz ) odvodíme jednodušší vztah než je v rovnici
(1.5.6).
Vektorový potenciál za předpokladu zanedbání retardace je stejný jako pro stacionární magnetické pole vytvořené proudem
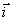 tedy
tedy
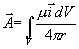 (viz.[3] str. 18 a 40).
Úvahou je možné odvodit analogický vzorec pro skalární potenciál, který splňuje Poissonovu rovnici typu
(viz.[3] str. 18 a 40).
Úvahou je možné odvodit analogický vzorec pro skalární potenciál, který splňuje Poissonovu rovnici typu
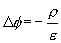 .
.
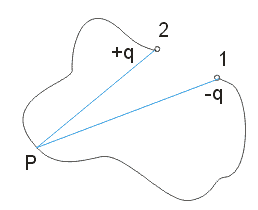
Na základě Coulombova zákona
náboj 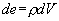 vytváří ve vzdálenosti
r od sebe potenciál
vytváří ve vzdálenosti
r od sebe potenciál
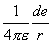 .
Pro potenciál platí princip superpozice.
Celkový potenciál
.
Pro potenciál platí princip superpozice.
Celkový potenciál
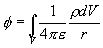 .
.
Vzorec pro 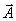 je duální modifikací
je duální modifikací
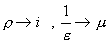 .
Proudovou hustotu můžeme vyjádřit jako součin celkového proudu
I a vektorové funkce
.
Proudovou hustotu můžeme vyjádřit jako součin celkového proudu
I a vektorové funkce
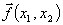 , kde x1,x2 jsou souřadnice přes průřez vodiče:
, kde x1,x2 jsou souřadnice přes průřez vodiče:
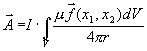 . Vlastní integrál je funkcí μ,
relativního rozložení proudu a konfigurace obvodu, ale nikoli celkového proudu
I.
. Vlastní integrál je funkcí μ,
relativního rozložení proudu a konfigurace obvodu, ale nikoli celkového proudu
I.
Můžeme proto definovat koeficient
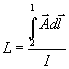 (1.6.1).
(1.6.1).
Příslušný člen v rovnici (1.5.6)
přejde na tvar:
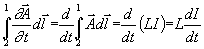
Parciální derivaci jsme nahradili totální derivací, neboť z našich předpokladů vyplývá, že podél obvodu se
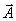 nebude měnit jako funkce místa
- stacionarita.
nebude měnit jako funkce místa
- stacionarita.
Definici (1.6.1) pro indukčnost lze, pokud uvažujeme uzavřený
obvod, napsat v jednodušším tvaru.
Platí
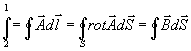
a tedy
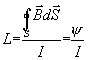 ,
,
kde 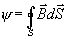 je magnetický tok plochou obvodu.
je magnetický tok plochou obvodu.
Kapacitní člen
Zatím jsme předpokládali, že obvod je uzavřený. Když nyní obvod v jednom místě rozpojíme, vznikne přechod mezi prostředími o různém
ε a vznikne možnost akumulace náboje.
Vyjádříme-li
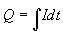 (rovnice kontinuity), dostaneme pro
(rovnice kontinuity), dostaneme pro kapacitní
spád vztah:
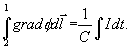
Předpokládáme-li periodicky proměnné napětí a proudy, můžeme napsat pro komplexní amplitudy těchto proudů :
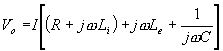 .
.
<<< předchozí | hlavní stránka
| další >>>
![]() a obvodem neteče proud, pokud nebude úplně uzavřen. Integrály
a obvodem neteče proud, pokud nebude úplně uzavřen. Integrály
![]() ... jsou
integrály křivkové podél uzavřené křivky:
... jsou
integrály křivkové podél uzavřené křivky:
![]() , protože φ
je prostý skalár nezávislý na čase. Proudovou hustotu
, protože φ
je prostý skalár nezávislý na čase. Proudovou hustotu
![]() vypočítáme z celkového protékajícího proudu:
vypočítáme z celkového protékajícího proudu:
![]() , kde
A je plocha průřezu vodiče. Pak
, kde
A je plocha průřezu vodiče. Pak
![]() =
=
![]() (
I a dl mají stejný směr)
⇒ I
(
I a dl mají stejný směr)
⇒ I
![]() (A
přitom může být funkcí I).
Integrál u I
se nazývá stejnosměrný odpor R dráhy 21 a platí integrální Ohmův zákon
(A
přitom může být funkcí I).
Integrál u I
se nazývá stejnosměrný odpor R dráhy 21 a platí integrální Ohmův zákon
![]() .
.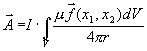 . Vlastní integrál je funkcí μ,
relativního rozložení proudu a konfigurace obvodu, ale nikoli celkového proudu
I.
. Vlastní integrál je funkcí μ,
relativního rozložení proudu a konfigurace obvodu, ale nikoli celkového proudu
I.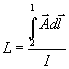
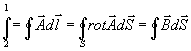
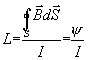 ,
,
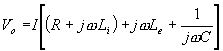 .
.