3.2 Geometrická optika sférických ploch
Pod pojmem geometrická optika se většinou chápe nauka zabývající se průchodem optických paprsků čočkami, zrcadly a jinými zobrazovacími prvky, tedy optickým zobrazením. Z hlediska základních zákonů fyziky stačí pro naprostou většinu vyšetřovaných případů znalost zákona lomu. Šíření světla soustavou je pak možné studovat tak, že z jednotlivých bodů předmětu necháme vystupovat myšlené paprsky pod různými směry a necháme je lámat a odrážet na jednotlivých optických rozhraních. Současné počítače tak dovolují vyšetřit šíření velkého počtu paprsků a úlohu vyřešit. Této metodě se říká obvykle metoda sledování paprsků ("ray tracing"). Po staletí se však vyvíjely i jiné postupy výpočtu zobrazovacích soustav v různých stupních aproximací. Byly také řešeny základní otázky související s optickým zobrazením, tedy co to je dokonalé zobrazení, jaká matematická transformace mu odpovídá a za jakých experimentálních podmínek je možné ho realizovat. Nebudeme se zde obecně těmito problémy zabývat, jejich diskusi je možné nalézt například v knize Borna a Wolfa. Připomeneme pouze, že při ideálním zobrazení odpovídá každému bodu předmětového prostoru právě jeden bod prostoru obrazového (sdružené body), podobně každé úsečce, resp. rovině, odpovídá sdružená úsečka, resp. rovina. Obraz vytvořený v rovině kolmé k ose soustavy (v osově symetrické soustavě) je v geometrickém smyslu podobný předmětu.
Omezíme se zde na případ zobrazení, ke kterému dochází při lomu světla na kulových rozhraních mezi prostředími s různými indexy lomu a při odrazu světla na kulových zrcadlech. Budeme se zabývat nejjednodušším případem, kdy paprsky šířící se osově symetrickou soustavou svírají malé úhly s osou soustavy. Tento případ se nazývá paraxiální aproximací. Odvodíme příslušné zobrazovací rovnice, které spojují souřadnice vzoru a obrazu. Vzhledem k osové souměrnosti zobrazovacích soustav stačí užívat dvě souřadnice, "příčnou" ve směru kolmém k ose soustavy, kterou budeme označovat y, a podélnou ve směru optické osy, kterou budeme označovat z. K zvláštnostem geometrické optiky patří, že se zavádí při výpočtu celá řada souřadných soustav: s každým optickým prvkem je spojena souřadná soustava předmětová (v předmětovém prostoru) a souřadná soustava obrazová (v obrazovém prostoru). Důvodem je skutečnost, že zobrazovací rovnice je možné psát ve stejném tvaru pro každý optický prvek.
3.2.1 Znaménková konvence
K další zvláštnosti geometrické optiky patří znaménková konvence, která zavádí vzdálenosti a úhly jako orientované veličiny. Důsledně užívaná konvence umožňuje používat zobrazovací rovnice ve stejném tvaru pro různé případy, a získat přímočaře výsledky se správnými znaménky (například, zda je čočka spojná či rozptylná). Ke koloritu geometrické optiky patří, že většina učebnic a knih užívá znaménkovou konvenci, ale každá jinou. Zvolená konvence vede ovšem k jisté modifikaci rovnic a vztahů geometrické optiky, proto je nutné převzít vztahy i s příslušnou konvencí. Zavedeme zde znaménkovou konvenci, kterou dále budeme v geometrické optice užívat. Vycházíme přitom z konvence normy DIN 1335.
Kladné jsou všechny dráhy a úsečky odměřované od vztažného bodu ve směru šíření světelných paprsků a od vztažného bodu směrem nahoru. Schémata se zakreslují tak, že světlo se šíří zleva doprava, po odraze na zrcadle může být ovšem směr opačný. Vzdálenosti se znázorňují orientovanými úsečkami s počátkem ve vztažném bodě. Vztažnými body jsou:
- pro kulové plochy body na ploše (poloměr křivosti je orientován od bodu na ploše do středu křivosti plochy);
- pro ohniskové vzdálenosti příslušné hlavní body (ohnisková vzdálenost je orientována od hlavního bodu k ohniskovému bodu);
- pro souřadnice bodů počátky odpovídajících souřadných systémů, obvykle buď hlavní body nebo ohniska. Souřadnice v souřadném systému s počátkem v hlavním bodě se označují malými písmeny, tj. x, y, z, v souřadném systému spojeném s ohnisky velkými písmeny, tj. X, Y, Z). Pro souřadnici z měřenou od hlavního bodu se často z historických důvodů používá označení a. U kulových ploch se často měří vzdálenost od vrcholu lámavé plochy (vztažný bod), která se označuje s.
Úhly se měří od vztažného ramene k druhému rameni. Pokud postupujeme od vztažného ramene k druhému rameni v kladném smyslu (proti směru pohybu hodinových ručiček) je úhel kladný. Vztažným ramenem je:
- pro úhly dopadu kolmice dopadu
- pro úhly paprsků a poloměrů křivosti paprsky a poloměry křivosti (například úhel, který svírá paprsek s osou soustavy se měří od paprsku k ose).
Uvedená znaménková konvence je ilustrována na obr.10. 5.
 Obr. 10.5
Obr. 10.5 Ilustrace znaménkové konvence. Paprsek vycházející z bodu
P dopadá po průchodu optickou soustavou do bodu
P
3.2.2 Abbéův invariant
 Obr. 10.6
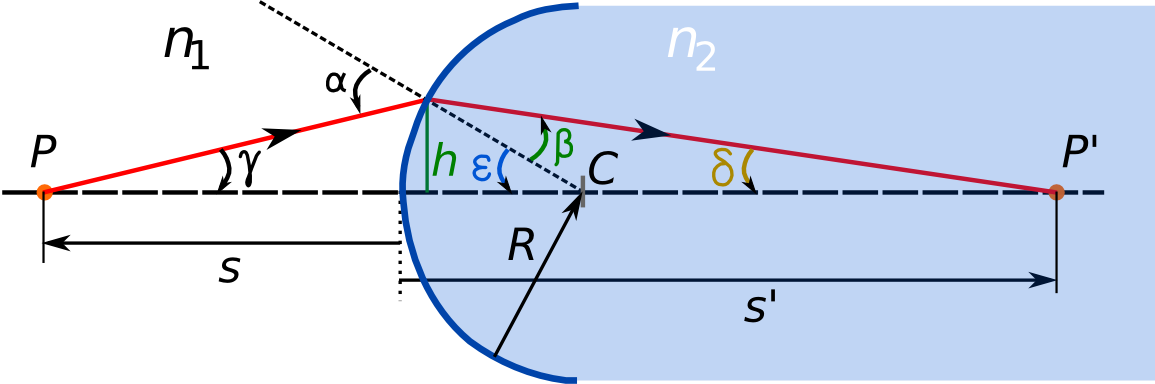
Obr. 10.6 K odvození Abbéovy rovnice pro lom paprsků na kulovém optickém rozhraní
Nyní se budeme zabývat lomem a odrazem světla na kulovém optickém rozhraní. Na obr. 10.6 je znázorněna kulová plocha o poloměru R se středem v bodě C, která odděluje prostředí s indexem lomu
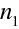 a
a
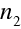 . Z bodu P vychází paprsek, který dopadá na optické rozhraní a láme se do bodu
. Z bodu P vychází paprsek, který dopadá na optické rozhraní a láme se do bodu
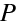 . Přímka
. Přímka
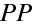 prochází středem křivosti plochy, v uvedeném kontextu se nazývá osou zobrazovacího prvku. Vzdálenost bodu, v němž dopadá paprsek na kulové rozhraní je ve vzdálenosti h od osy
prochází středem křivosti plochy, v uvedeném kontextu se nazývá osou zobrazovacího prvku. Vzdálenost bodu, v němž dopadá paprsek na kulové rozhraní je ve vzdálenosti h od osy
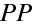 . Vzdálenosti bodu P, resp.
. Vzdálenosti bodu P, resp.
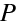 , od vrcholu kulové plochy jsou s, resp.
, od vrcholu kulové plochy jsou s, resp.
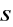 . Budeme je udávat v zavedené konvenci geometrické optiky. Na obr. 10.6 jsou vyznačeny úhly (je použita znaménková konvence). Z geometrie zřejmě plyne
. Budeme je udávat v zavedené konvenci geometrické optiky. Na obr. 10.6 jsou vyznačeny úhly (je použita znaménková konvence). Z geometrie zřejmě plyne
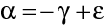 |
(10.49) |
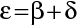 |
(10.50) |
Budeme dále předpokládat, že vzdálenost h je malá, tak že úhly jsou natolik malé, že jejich tangenty můžeme nahradit s dobrou přesností jejich argumenty. Tato aproximace se nazývá paraxiální aproximací. V uvedené aproximaci platí
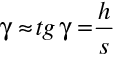 |
(10.51) |
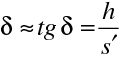 |
(10.52) |
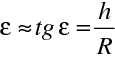 |
(10.53) |
Podle zákona lomu v paraxiální aproximaci ovšem platí
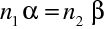 |
(10.54) |
Ze vztahů (10.49, 10.50) a (10.54) máme
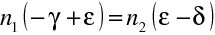 |
(10.55) |
a
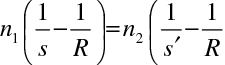 |
(10.56) |
To je rovnice spojuje vzdálenost s, se vzdáleností
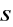 , vystupují v ní pouze indexy lomu a poloměr kulové plochy. To znamená, že všechny paprsky vycházející pod libovolným úhlem vůči ose z bodu P dopadají do jednoho bodu
, vystupují v ní pouze indexy lomu a poloměr kulové plochy. To znamená, že všechny paprsky vycházející pod libovolným úhlem vůči ose z bodu P dopadají do jednoho bodu
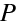 na ose (stigmatické zobrazení). Levá i pravá strana rovnice (10.56) má stejný tvar, nazývá se často Abbéovým invariantem.
Jak se zobrazují body, které neleží na ose ? Uvažujme bod vzdálený y od osy, který se zobrazí do bodu vzdáleného
na ose (stigmatické zobrazení). Levá i pravá strana rovnice (10.56) má stejný tvar, nazývá se často Abbéovým invariantem.
Jak se zobrazují body, které neleží na ose ? Uvažujme bod vzdálený y od osy, který se zobrazí do bodu vzdáleného
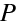 od osy. V paraxiální aproximaci pro zobrazení bodu, který leží ve vzdálenosti y nad osou, můžeme nalézt vzdálenost
od osy. V paraxiální aproximaci pro zobrazení bodu, který leží ve vzdálenosti y nad osou, můžeme nalézt vzdálenost
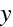 jeho obrazu od osy jednoduše z geometrie, jak je uvedeno na obr. 10.7 . Zřejmě platí
jeho obrazu od osy jednoduše z geometrie, jak je uvedeno na obr. 10.7 . Zřejmě platí
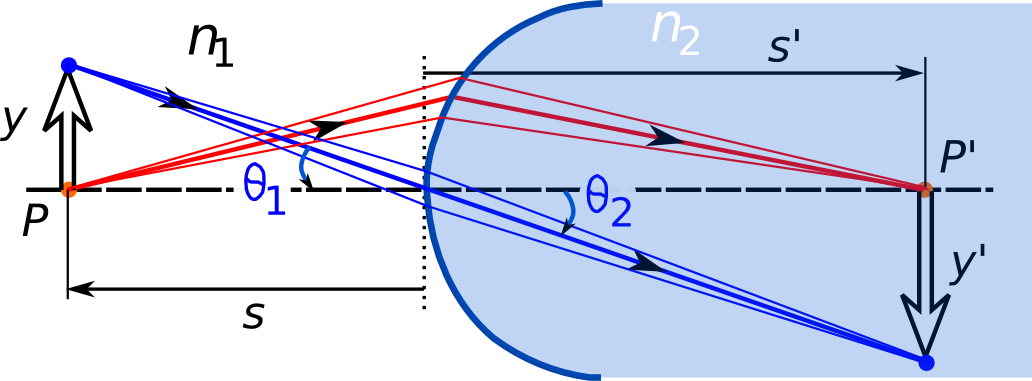 Obr. 10.7
Obr. 10.7 K výkladu příčného zvětšení při lomu na kulové ploše
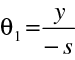 |
(10.57) |
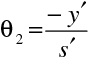 |
(10.58) |
Podle zákona lomu
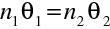 |
(10.59) |
Z rov. (10.57 - 59) máme vztah pro příčné zvětšení
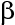
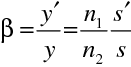 |
(10.60) |
3.2.3 Kardinální body optické soustavy
V geometrické optice se pro jednotlivé zobrazovací soustavy definují důležité, tzv. kardinální body. K nim patří ohniskové, hlavní a uzlové body. Uvedeme nyní jejich definici a ukážeme, jak je možné určit jejich polohu pro kulovou lámavou plochu.
Hlavní body optické soustavy jsou navzájem sdružené (vzor - obraz) body
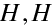 , které jsou průsečíky předmětové a obrazové hlavní roviny (roviny kolmé k optické ose). Hlavní roviny jsou navzájem sdružené, a mají tu vlastnost, že příčné zvětšení je při zobrazení rovno jedné. Tedy rovnost
, které jsou průsečíky předmětové a obrazové hlavní roviny (roviny kolmé k optické ose). Hlavní roviny jsou navzájem sdružené, a mají tu vlastnost, že příčné zvětšení je při zobrazení rovno jedné. Tedy rovnost
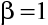 |
(10.61) |
je podmínkou pro hlavní roviny. V případě kulové lámavé plochy je z názoru zřejmé (zákon lomu), že budeme-li posunovat předmět (úsečku
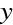 ) podél osy, dostaneme vždy obraz, pro nějž
) podél osy, dostaneme vždy obraz, pro nějž
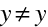 . Výjimkou bude případ, kdy se zobrazuje bod ležící na optickém rozhraní, kdy ovšem splývá bod a obraz. Protože je optické rozhraní tvořeno kulovou plochou, měli bychom místo hlavní roviny "hlavní kulovou plochu". Ale v paraxiální aproximaci je obraz umístěn tak blízko osy, že kulovou plochu můžeme aproximovat rovinou. U kulového rozhraní tedy v paraxiální aproximaci obě hlavní roviny splývají a procházejí vrcholem lámavé plochy, hlavní body
. Výjimkou bude případ, kdy se zobrazuje bod ležící na optickém rozhraní, kdy ovšem splývá bod a obraz. Protože je optické rozhraní tvořeno kulovou plochou, měli bychom místo hlavní roviny "hlavní kulovou plochu". Ale v paraxiální aproximaci je obraz umístěn tak blízko osy, že kulovou plochu můžeme aproximovat rovinou. U kulového rozhraní tedy v paraxiální aproximaci obě hlavní roviny splývají a procházejí vrcholem lámavé plochy, hlavní body
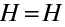 leží ve vrcholu (vrcholem se myslí průsečík optické osy s lámavou plochou).
leží ve vrcholu (vrcholem se myslí průsečík optické osy s lámavou plochou).
Jak jsou definované ohniskové body ? Předmětový
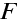 a obrazový
a obrazový
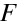 ohniskový bod nejsou navzájem sdružené body, jsou to průsečíky odpovídajících ohniskových rovin s optickou osou. Předmětová ohnisková rovina je rovina (kolmá k optické ose ), jejíž body se zobrazí do nekonečna. Obrazová ohnisková rovina je rovina, do níž se zobrazí body ležící v nekonečnu (v "minus nekonečnu" podle znaménkové konvence). Ohniskové body
ohniskový bod nejsou navzájem sdružené body, jsou to průsečíky odpovídajících ohniskových rovin s optickou osou. Předmětová ohnisková rovina je rovina (kolmá k optické ose ), jejíž body se zobrazí do nekonečna. Obrazová ohnisková rovina je rovina, do níž se zobrazí body ležící v nekonečnu (v "minus nekonečnu" podle znaménkové konvence). Ohniskové body
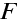 ,
,
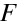 jsou sdružené s body, které leží v nekonečnu na optické ose. Kde leží ohniskové body kulové lámavé plochy ? Abbéův invariant můžeme přepsat
jsou sdružené s body, které leží v nekonečnu na optické ose. Kde leží ohniskové body kulové lámavé plochy ? Abbéův invariant můžeme přepsat
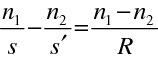 |
(10.62) |
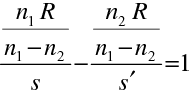 |
(10.63) |
Polohu obrazového ohniskového bodu určíme, když si uvědomíme, že je obrazem bodu ležícího v nekonečnu, tedy z podmínky
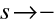 :
:
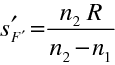 |
(10.64) |
Podobně pro polohu předmětového ohniska
 ,
,
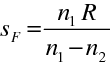 |
(10.65) |
Ohniskové vzdálenosti, jak jsme uvedli již při zavádění znaménkové konvence, se definují jako orientované vzdálenosti měřené od hlavních bodů k ohniskovým bodům. Předmětová ohnisková vzdálenost f je rovna
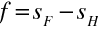 |
(10.66) |
a obrazová ohnisková vzdálenost

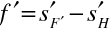 |
(10.67) |
Pro lom na kulové ploše je, jak jsme uvedli,
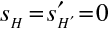 , proto
, proto
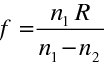 |
(10.68) |
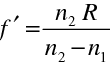 |
(10.69) |
Pro podíl ohniskových vzdáleností dostáváme 
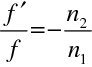 |
(10.70) |
Uvidíme později, že tento vztah mezi obrazovým a předmětovým ohniskem platí obecně i pro složitější optické soustavy. Uzlové body N, N` jsou dva sdružené body, pro které je úhlové zvětšení rovno jedné, jak uvedeme v odstavci 10.2.6.
3.2.4 Zobrazovací rovnice
Abbéův invariant ve tvaru (10.63) můžeme přepsat do jednoduchého tvaru, který spojuje vzdálenosti předmětu a obrazu pomocí ohniskových vzdáleností:
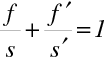 |
(10.71) |
Vzdálenosti s,
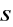 měřené od vrcholu lámavé plochy jsou v případě lomu na kulovém optickém rozhraní rovny vzdálenostem a,
měřené od vrcholu lámavé plochy jsou v případě lomu na kulovém optickém rozhraní rovny vzdálenostem a,
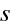 měřeným od hlavních bodů, protože hlavní body leží ve vrcholu lámavé plochy. Můžeme tedy psát
měřeným od hlavních bodů, protože hlavní body leží ve vrcholu lámavé plochy. Můžeme tedy psát
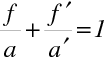 |
(10.72) |
což je známý Gaussův tvar zobrazovací rovnice. Také příčné zvětšení je možné vyjádřit pomocí vzdáleností a,
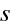
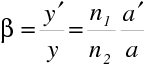 |
(10.73) |
Zobrazovací rovnice (10.72), (10.73) můžeme ovšem přepsat i pomocí vzdáleností měřených od ohniskových bodů. Stačí správně vyjádřit transformaci vzdáleností, která je zřejmá z obr. 10.8.
 Obr. 10.8
Obr. 10.8 Vztah mezi vzdálenostmi měřenými v soustavách spojených s hlavními a ohniskovými body
Podle obr. 10.8 zřejmě platí
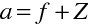 |
(10.74) |
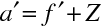 |
(10.75) |
Přímým dosazením rov. (10.74), (10.75) do rov. (10.72) máme
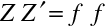 |
(10.76) |
a dosazením do (10.73)
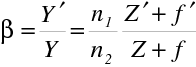 |
(10.77) |
a dále s uvážením (10.76)
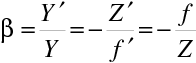 |
(10.78) |
Vztahy (10.76) a (10.78) se nazývají Newtonovy zobrazovací rovnice.
Gaussovy a Newtonovy zobrazovací vztahy (rovnice) jsou obecným tvarem rovnic pro optické zobrazení. Protože naprostá většina zobrazovacích prvků v optice je tvořena sférickými plochami, pro něž jsme ukázali platnost uvedených vztahů, nebudeme se jejich obecnější platností zabývat.
3.2.5 Zrcadlové plochy
Po odrazu světla se změní směr jeho šíření, světlo se šíří stále v prostředí se stejným indexem lomu, fázová rychlost tedy mění pouze znaménko. Úvahy a vztahy, které jsme uvedli výše pro lom světla na rozhraní mezi prostředími s indexy lomu n1, n2, můžeme použít i na případ odrazu světla, položíme-li formálně
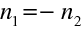 |
(10.79) |
Pak podle rov. (10.64), (10.65), resp. (10.68) a (10.69) je
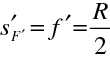 |
(10.80) |
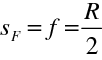 |
(10.81) |
Zřejmě je
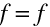 |
(10.82) |
jak také vychází z (10.70) pro
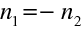 . Zobrazovací vztah (10.72) pro zrcadlo lze tedy psát
. Zobrazovací vztah (10.72) pro zrcadlo lze tedy psát
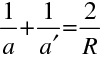 |
(10.83) |
Pro příčné zvětšení (10.73) vychází pro (10.79)
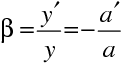 |
(10.84) |
Kulová zrcadla se dají rozdělit na vypuklá (konvexní) a dutá (konkávní). V souhlasu se zde používanou znaménkovou konvencí je pro vypuklá zrcadla jejich poloměr R>0, pro zrcadla dutá je R<0. Pro předmět před zrcadlem je a< 0. Z (10.83) tedy pro vypuklá zrcadla plyne
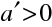 , tedy, že obraz vzniká v prostoru za zrcadlem, je virtuální. Podle (10.84) je b >0 , obraz je vzpřímený. Pro dutá zrcadla (R<0) pro
, tedy, že obraz vzniká v prostoru za zrcadlem, je virtuální. Podle (10.84) je b >0 , obraz je vzpřímený. Pro dutá zrcadla (R<0) pro
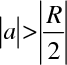 je
je
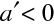 , a
, a
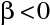 , tedy obraz vzniká v prostoru před zrcadlem, je tedy reálný, a je převrácený. Pro dutá zrcadla pro
, tedy obraz vzniká v prostoru před zrcadlem, je tedy reálný, a je převrácený. Pro dutá zrcadla pro
 je
je
 , a
, a
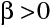 , což znamená, že obraz je virtuální a vzpřímený. K uvedeným závěrům lze dospět také pomocí geometrické konstrukce, v případě zrcadel obzvlášť jednoduché (použití dvou speciálních paprsků vycházejících z bodu předmětu: jeden paprsek procházející (eventuálně v prodloužení za zrcadlo) středem poloměru křivosti zrcadla zachovává při odrazu svůj směr, druhý paprsek procházející ohniskem se šíří po odrazu rovnoběžně s osou).
, což znamená, že obraz je virtuální a vzpřímený. K uvedeným závěrům lze dospět také pomocí geometrické konstrukce, v případě zrcadel obzvlášť jednoduché (použití dvou speciálních paprsků vycházejících z bodu předmětu: jeden paprsek procházející (eventuálně v prodloužení za zrcadlo) středem poloměru křivosti zrcadla zachovává při odrazu svůj směr, druhý paprsek procházející ohniskem se šíří po odrazu rovnoběžně s osou).
Kulová zrcadla zajišťují ovšem ideální zobrazení pouze v paraxiální aproximaci. Pro obecný případ dochází k vadám zobrazení. Zrcadlová koule (vánoční ozdoba) dovoluje ovšem (zkresleně) zobrazit téměř celý prostor kolem ní. Skutečně, pozorujeme-li kouli o poloměru R z velké vzdálenosti, dopadají do oka paprsky (přibližně rovnoběžné), jejichž úhel odrazu se při změně záměrné vzdálenosti od středu koule k jejím krajům mění od 0 do 180o. V kouli lze vidět vše, kromě prostoru za ní. Uvedené zobrazení prostoru (které studoval podobně Helmholtz) hraje jistou roli v teorii relativity.
3.2.6 Zvětšení při optickém zobrazení
Příčné zvětšení v paraxiální aproximaci jsme uvedli výše
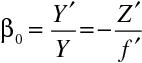 resp.
resp.
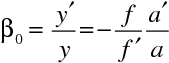
|
(10.85) |
Hlavní roviny jsou definovány podmínkou
 . Úhlové zvětšení je definováno (
. Úhlové zvětšení je definováno (
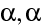 jsou úhly, které svírá paprsek s osou z) jako
jsou úhly, které svírá paprsek s osou z) jako
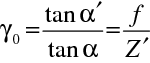 resp.
resp.
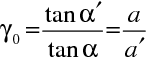
|
(10.86) |
Uzlové body jsou určeny podmínkou
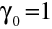 .V případě, kdy
.V případě, kdy
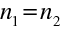 , tedy, kdy je například před čočkou i za čočkou prostředí se stejným indexem lomu, uzlové a hlavní body splývají, jak plyne přímo z rov. (10.70), (10.85) a (10.86).
Podélné zvětšení je definováno
, tedy, kdy je například před čočkou i za čočkou prostředí se stejným indexem lomu, uzlové a hlavní body splývají, jak plyne přímo z rov. (10.70), (10.85) a (10.86).
Podélné zvětšení je definováno
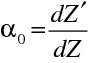 |
(10.87) |
Diferencováním rovnice (10.76)
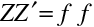 dostaneme
dostaneme
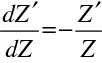 |
(10.88) |
nebo
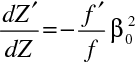 |
(10.89) |
Z výše uvedených vztahů pak máme
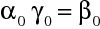 |
(10.90) |
Pro častý případ
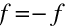 pak platí
pak platí
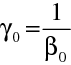 |
(10.91) |
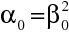 |
(10.92) |
3.2.7 Kombinace dvou zobrazení
 Obr. 10.9
Obr. 10.9 Kombinace dvou zobrazení
Podíváme se nyní na situaci, kdy je zobrazovací prvek tvořen kombinací dvou jednodušších prvků, jejichž zobrazení je popsáno zobrazovacími vztahy (10.76), (10.78). To odpovídá například zobrazení lomem na dvou po sobě následujících kulových plochách. Situace je znázorněna na obr. 10.9. Budeme používat Newtonovy zobrazovací vztahy a tedy souřadné systémy spojené s ohniskovými body. První zobrazovací prvek je charakterizován ohniskovými body
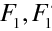 a ohniskovými vzdálenostmi
a ohniskovými vzdálenostmi
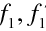 , druhý prvek má ohniskové body
, druhý prvek má ohniskové body
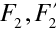 a vzdálenosti
a vzdálenosti
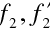 . Předpokládáme, že oba prvky jsou umístěny tak, aby jejich optické osy splývaly. Vzdálenost mezi oběma prvky se obvykle vyjadřuje pomocí optického intervalu
. Předpokládáme, že oba prvky jsou umístěny tak, aby jejich optické osy splývaly. Vzdálenost mezi oběma prvky se obvykle vyjadřuje pomocí optického intervalu
 , tedy vzdálenosti měřené od obrazového ohniska
, tedy vzdálenosti měřené od obrazového ohniska
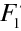 prvního prvku k předmětovému ohnisku
prvního prvku k předmětovému ohnisku
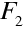 druhého prvku. Uvažujme nyní předmět znázorněný šipkou, jejíž koncový bod má v předmětovém prostoru prvního prvku souřadnice
druhého prvku. Uvažujme nyní předmět znázorněný šipkou, jejíž koncový bod má v předmětovém prostoru prvního prvku souřadnice
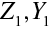 . První prvek vytvoří obraz, který má v jeho obrazovém prostoru souřadnice
. První prvek vytvoří obraz, který má v jeho obrazovém prostoru souřadnice
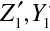 . Obrazový prostor prvního prvku je ovšem současně předmětovým prostorem prvku druhého, souřadnice předmětu pro druhý zobrazovací prvek jsou
. Obrazový prostor prvního prvku je ovšem současně předmětovým prostorem prvku druhého, souřadnice předmětu pro druhý zobrazovací prvek jsou
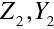 . Souřadnice výsledného obrazu v obrazovém prostoru druhého prvku jsou
. Souřadnice výsledného obrazu v obrazovém prostoru druhého prvku jsou
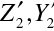 . Podle obrázku zřejmě platí
. Podle obrázku zřejmě platí
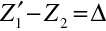 |
(10.93) |
Dále platí zobrazovací vztahy
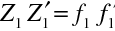 |
(10.94) |
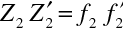 |
(10.95) |
Nyní najdeme polohu ohniskových a hlavních bodů kombinace dvou zobrazení a ukážeme, že i pro výslednou kombinaci platí opět Newtonovy zobrazovací vztahy. Z (10.93) a (10.94) dostaneme
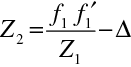 |
(10.96) |
a z (10.95)
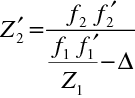 |
(10.97) |
Odtud můžeme určit polohu výsledných ohniskových bodů: souřadnici obrazového ohniskového bodu
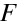 (souřadnice v soustavě spojené s obrazovým ohniskem
(souřadnice v soustavě spojené s obrazovým ohniskem
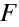 ) dostaneme z (10.97) v limitě
) dostaneme z (10.97) v limitě
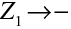
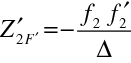 |
(10.98) |
Podobně pro
 máme pro polohu předmětového ohniska
máme pro polohu předmětového ohniska
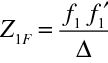 |
(10.99) |
Tyto polohy ohniska jsme mohli ovšem určit i jednodušším způsobem: paprsky přicházející rovnoběžně s osou se protnou v ohniskovém bodě prvního prvku (například čočky)
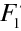 . Tento prvotní obraz je dále zobrazován druhou čočkou, podle Newtonova vztahu (10.76) dostaneme výsledek (10.98), uvážíme-li, že
. Tento prvotní obraz je dále zobrazován druhou čočkou, podle Newtonova vztahu (10.76) dostaneme výsledek (10.98), uvážíme-li, že
 . Odtud je zřejmé, proč ve vztahu (10.98) nevystupuje ohnisková vzdálenost první čočky. Podobnou úvahu můžeme provést i pro předmětové ohnisko.
. Odtud je zřejmé, proč ve vztahu (10.98) nevystupuje ohnisková vzdálenost první čočky. Podobnou úvahu můžeme provést i pro předmětové ohnisko.
Určíme nyní polohu hlavních bodů složené soustavy. Pro příčné zvětšení prvního a druhého prvku máme
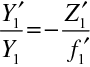 |
(10.100) |
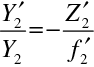 |
(10.101) |
Je jasné, že
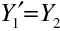 . Vydělením rovnic (10.100) a (10.101) a dosazením z (10.94) resp. (10.97) dostaneme pro příčné zvětšení celé soustavy
. Vydělením rovnic (10.100) a (10.101) a dosazením z (10.94) resp. (10.97) dostaneme pro příčné zvětšení celé soustavy
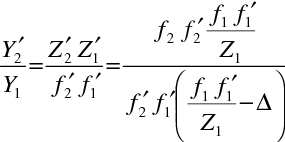 |
(10.102) |
Polohu předmětového hlavního bodu dostaneme nyní jednoduše z (10.102) a z podmínky
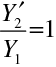 , která hlavní body definuje:
, která hlavní body definuje:
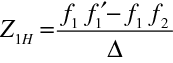 |
(10.103) |
Pro polohu obrazového hlavního bodu máme například z (10.97)
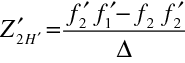 |
(10.104) |
Výsledné ohniskové vzdálenosti můžeme určit z jejich definice jako vzdálenosti měřené od hlavních bodů k ohniskovým bodům, tedy
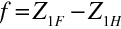 |
(10.105) |
a
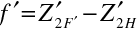 |
(10.106) |
Dosazením z rov. (10.98, 10.99) a (10.103, 10.105) máme výsledek
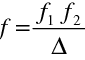 |
(10.107) |
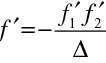 |
(10.108) |
Pro kombinaci dvou zobrazení jsme tedy dostali polohu ohniskových a hlavních bodů a velikosti ohniskových vzdáleností. Vyjádříme-li nyní souřadnice obrazu a vzoru v souřadném systému spojeném s výslednými ohniskovými body
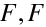 , můžeme přímo ukázat, že pro výsledné zobrazení platí obecné Newtonovy zobrazovací vztahy (10.76, 10.78).
, můžeme přímo ukázat, že pro výsledné zobrazení platí obecné Newtonovy zobrazovací vztahy (10.76, 10.78).
Uvedeným postupem můžeme kombinovat libovolný počet zobrazovacích prvků.
3.2.8 Optická čočka
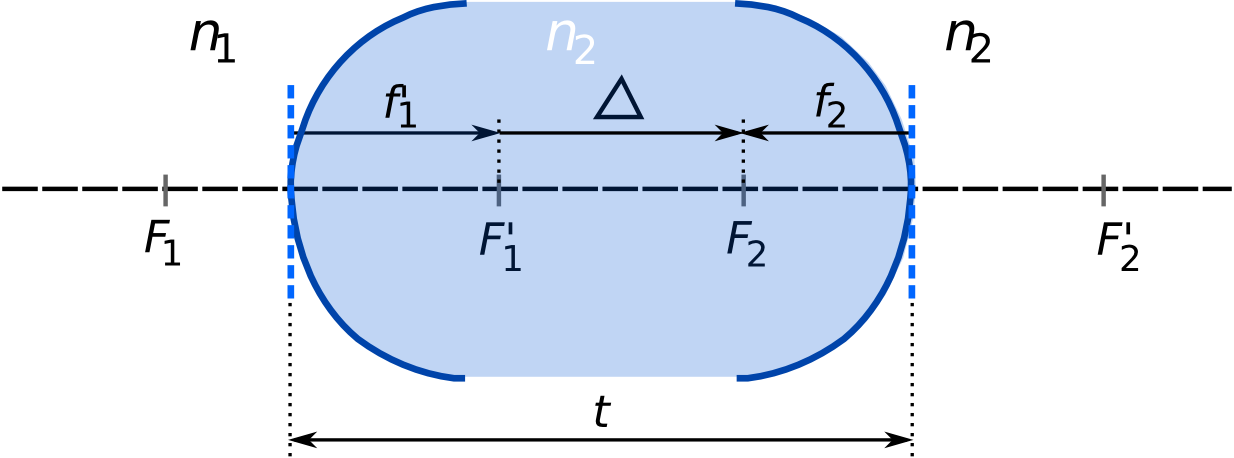 Obr. 10.10
Obr. 10.10 Schéma obecné čočky, tedy dvou kulových ploch oddělujících tři prostředí s indexy lomu
n1, n 2, n 3.
Optická čočka je zobrazovací prvek, který je tvořen kombinací dvou sférických lámavých ploch. Nejčastěji je čočka vyrobena ze skla a je umístěna ve vzduchu. Na obr.10.10 je znázorněna obecná čočka, tj. kombinace dvou lámavých ploch s poloměry
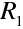 a
a
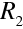 , které oddělují prostředí s indexy lomu postupně
, které oddělují prostředí s indexy lomu postupně
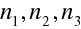 . Osou zobrazovací soustavy je přímka spojující středy křivosti obou ploch. Tloušťka čočky t je kladná geometrická vzdálenost vrcholů obou ploch. Tloušťka čočky je spojena s optickým intervalem a ohniskovými vzdálenostmi obou lámavých ploch, jak je zřejmé z obrázku
. Osou zobrazovací soustavy je přímka spojující středy křivosti obou ploch. Tloušťka čočky t je kladná geometrická vzdálenost vrcholů obou ploch. Tloušťka čočky je spojena s optickým intervalem a ohniskovými vzdálenostmi obou lámavých ploch, jak je zřejmé z obrázku
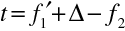 . Užíváme zde, stejně jako všude v této kapitole, znaménkovou konvenci. Pro ohniskové vzdálenosti obou lámavých ploch platí
. Užíváme zde, stejně jako všude v této kapitole, znaménkovou konvenci. Pro ohniskové vzdálenosti obou lámavých ploch platí
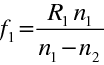 |
(10.109) |
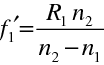 |
(10.110) |
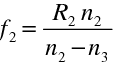 |
(10.111) |
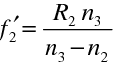 |
(10.112) |
Výsledné ohniskové vzdálenosti a polohu hlavních a ohniskových bodů dostaneme jednoduše dosazením do vztahů, které jsme odvodili pro kombinaci dvou zobrazení (10.101) až (10.106). Například pro čočku ve vzduchu, tedy pro
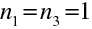 dostaneme pro výslednou ohniskovou vzdálenost
dostaneme pro výslednou ohniskovou vzdálenost
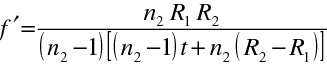 |
(10.113) |
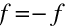 |
(10.114) |
Pokud je tloušťka čočky velmi malá, je možné ji zanedbat a položit tedy
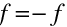 . V tomto případě se mluví o tenké čočce, na rozdíl od případu čočky tlusté. Tenká čočka je zřejmě aproximací, která se však velmi často používá pro jednoduchost výrazů. V aproximaci tenké čočky ve vzduchu můžeme psát výraz pro obrazovou ohniskovou vzdálenost ve tvaru
. V tomto případě se mluví o tenké čočce, na rozdíl od případu čočky tlusté. Tenká čočka je zřejmě aproximací, která se však velmi často používá pro jednoduchost výrazů. V aproximaci tenké čočky ve vzduchu můžeme psát výraz pro obrazovou ohniskovou vzdálenost ve tvaru
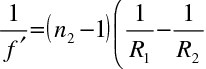 |
(10.115) |
kterému se často říká rovnice výrobců čoček, protože dovoluje pro daný index lomu skla čočky zvolit vhodné poloměry křivosti jejích ploch, aby měla požadovanou ohniskovou vzdálenost. Opět samozřejmě platí (10.114). Pro tenkou čočku, která je z materiálu o indexu lomu n2 v prostředí s indexem lomu
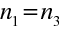 platí
platí
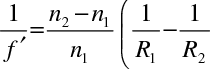 |
(10.116) |
V praxi se "síla" čočky umístěné v prostředí
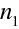 určuje pomocí optické mohutnosti , která se definuje
určuje pomocí optické mohutnosti , která se definuje
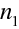 |
(10.117) |
Jednotkou optické mohutnosti je dioptrie (1D = 1/m). Pro čočku ve vzduchu je ovšem optická mohutnost rovna reciproké hodnotě obrazové ohniskové vzdálenosti. Znaménková konvence, kterou užíváme, dává znaménka optické mohutnosti v souhlase s tím, jak jsou používána v praxi, například u očních optiků; spojná čočka má kladnou optickou mohutnost.
Pro výpočet čočky jsou důležité samozřejmě i polohy kardinálních bodů, které můžeme přímo vypočítat ze vztahů (10.101 až 10.104). Z praktického hlediska je vhodné vyjádřit například polohu ohniskových bodů čočky pomocí jejich vzdáleností od vrcholů lámavých ploch. Pro případ čočky ve vzduchu je vzdálenost obrazového ohniska
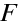 od vrcholu druhé lámavé plochy rovna
od vrcholu druhé lámavé plochy rovna
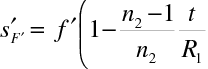 |
(10.118) |
a vzdálenost předmětového ohniska F od vrcholu první lámavé plochy je
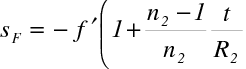 |
(10.119) |
Pro tenkou čočku je ovšem
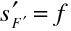 a
a
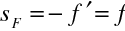 , což odpovídá tomu, že hlavní body leží pro tenkou čočku ve vrcholech obou sférických ploch, které splývají.
, což odpovídá tomu, že hlavní body leží pro tenkou čočku ve vrcholech obou sférických ploch, které splývají.


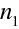 a
a
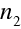 . Z bodu P vychází paprsek, který dopadá na optické rozhraní a láme se do bodu
. Z bodu P vychází paprsek, který dopadá na optické rozhraní a láme se do bodu
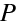 . Přímka
. Přímka
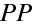 prochází středem křivosti plochy, v uvedeném kontextu se nazývá osou zobrazovacího prvku. Vzdálenost bodu, v němž dopadá paprsek na kulové rozhraní je ve vzdálenosti h od osy
prochází středem křivosti plochy, v uvedeném kontextu se nazývá osou zobrazovacího prvku. Vzdálenost bodu, v němž dopadá paprsek na kulové rozhraní je ve vzdálenosti h od osy
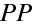 . Vzdálenosti bodu P, resp.
. Vzdálenosti bodu P, resp.
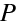 , od vrcholu kulové plochy jsou s, resp.
, od vrcholu kulové plochy jsou s, resp.
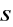 . Budeme je udávat v zavedené konvenci geometrické optiky. Na obr. 10.6 jsou vyznačeny úhly (je použita znaménková konvence). Z geometrie zřejmě plyne
. Budeme je udávat v zavedené konvenci geometrické optiky. Na obr. 10.6 jsou vyznačeny úhly (je použita znaménková konvence). Z geometrie zřejmě plyne
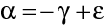
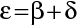
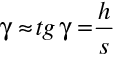
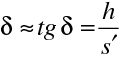
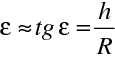
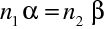
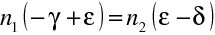
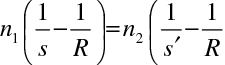
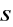 , vystupují v ní pouze indexy lomu a poloměr kulové plochy. To znamená, že všechny paprsky vycházející pod libovolným úhlem vůči ose z bodu P dopadají do jednoho bodu
, vystupují v ní pouze indexy lomu a poloměr kulové plochy. To znamená, že všechny paprsky vycházející pod libovolným úhlem vůči ose z bodu P dopadají do jednoho bodu
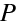 na ose (stigmatické zobrazení). Levá i pravá strana rovnice (10.56) má stejný tvar, nazývá se často Abbéovým invariantem.
Jak se zobrazují body, které neleží na ose ? Uvažujme bod vzdálený y od osy, který se zobrazí do bodu vzdáleného
na ose (stigmatické zobrazení). Levá i pravá strana rovnice (10.56) má stejný tvar, nazývá se často Abbéovým invariantem.
Jak se zobrazují body, které neleží na ose ? Uvažujme bod vzdálený y od osy, který se zobrazí do bodu vzdáleného
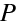 od osy. V paraxiální aproximaci pro zobrazení bodu, který leží ve vzdálenosti y nad osou, můžeme nalézt vzdálenost
od osy. V paraxiální aproximaci pro zobrazení bodu, který leží ve vzdálenosti y nad osou, můžeme nalézt vzdálenost
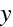 jeho obrazu od osy jednoduše z geometrie, jak je uvedeno na obr. 10.7 . Zřejmě platí
jeho obrazu od osy jednoduše z geometrie, jak je uvedeno na obr. 10.7 . Zřejmě platí

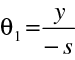
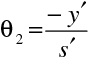
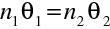
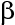
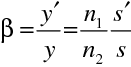
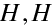 , které jsou průsečíky předmětové a obrazové hlavní roviny (roviny kolmé k optické ose). Hlavní roviny jsou navzájem sdružené, a mají tu vlastnost, že příčné zvětšení je při zobrazení rovno jedné. Tedy rovnost
, které jsou průsečíky předmětové a obrazové hlavní roviny (roviny kolmé k optické ose). Hlavní roviny jsou navzájem sdružené, a mají tu vlastnost, že příčné zvětšení je při zobrazení rovno jedné. Tedy rovnost
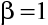
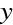 ) podél osy, dostaneme vždy obraz, pro nějž
) podél osy, dostaneme vždy obraz, pro nějž
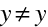 . Výjimkou bude případ, kdy se zobrazuje bod ležící na optickém rozhraní, kdy ovšem splývá bod a obraz. Protože je optické rozhraní tvořeno kulovou plochou, měli bychom místo hlavní roviny "hlavní kulovou plochu". Ale v paraxiální aproximaci je obraz umístěn tak blízko osy, že kulovou plochu můžeme aproximovat rovinou. U kulového rozhraní tedy v paraxiální aproximaci obě hlavní roviny splývají a procházejí vrcholem lámavé plochy, hlavní body
. Výjimkou bude případ, kdy se zobrazuje bod ležící na optickém rozhraní, kdy ovšem splývá bod a obraz. Protože je optické rozhraní tvořeno kulovou plochou, měli bychom místo hlavní roviny "hlavní kulovou plochu". Ale v paraxiální aproximaci je obraz umístěn tak blízko osy, že kulovou plochu můžeme aproximovat rovinou. U kulového rozhraní tedy v paraxiální aproximaci obě hlavní roviny splývají a procházejí vrcholem lámavé plochy, hlavní body
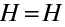 leží ve vrcholu (vrcholem se myslí průsečík optické osy s lámavou plochou).
leží ve vrcholu (vrcholem se myslí průsečík optické osy s lámavou plochou).
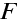 a obrazový
a obrazový
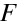 ohniskový bod nejsou navzájem sdružené body, jsou to průsečíky odpovídajících ohniskových rovin s optickou osou. Předmětová ohnisková rovina je rovina (kolmá k optické ose ), jejíž body se zobrazí do nekonečna. Obrazová ohnisková rovina je rovina, do níž se zobrazí body ležící v nekonečnu (v "minus nekonečnu" podle znaménkové konvence). Ohniskové body
ohniskový bod nejsou navzájem sdružené body, jsou to průsečíky odpovídajících ohniskových rovin s optickou osou. Předmětová ohnisková rovina je rovina (kolmá k optické ose ), jejíž body se zobrazí do nekonečna. Obrazová ohnisková rovina je rovina, do níž se zobrazí body ležící v nekonečnu (v "minus nekonečnu" podle znaménkové konvence). Ohniskové body
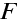 ,
,
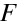 jsou sdružené s body, které leží v nekonečnu na optické ose. Kde leží ohniskové body kulové lámavé plochy ? Abbéův invariant můžeme přepsat
jsou sdružené s body, které leží v nekonečnu na optické ose. Kde leží ohniskové body kulové lámavé plochy ? Abbéův invariant můžeme přepsat
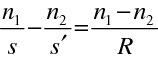
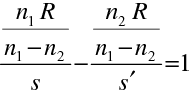
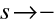 :
:
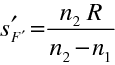
 ,
,
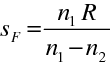
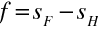

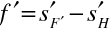
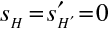 , proto
, proto

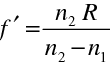

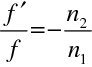
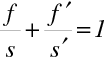
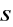 měřené od vrcholu lámavé plochy jsou v případě lomu na kulovém optickém rozhraní rovny vzdálenostem a,
měřené od vrcholu lámavé plochy jsou v případě lomu na kulovém optickém rozhraní rovny vzdálenostem a,
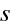 měřeným od hlavních bodů, protože hlavní body leží ve vrcholu lámavé plochy. Můžeme tedy psát
měřeným od hlavních bodů, protože hlavní body leží ve vrcholu lámavé plochy. Můžeme tedy psát
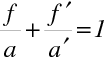
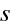
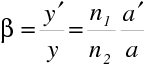

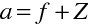
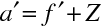
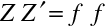
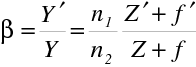
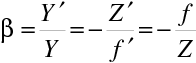
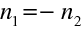
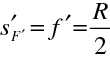
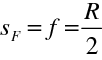
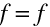
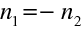 . Zobrazovací vztah (10.72) pro zrcadlo lze tedy psát
. Zobrazovací vztah (10.72) pro zrcadlo lze tedy psát
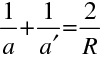
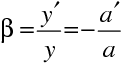
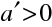 , tedy, že obraz vzniká v prostoru za zrcadlem, je virtuální. Podle (10.84) je b >0 , obraz je vzpřímený. Pro dutá zrcadla (R<0) pro
, tedy, že obraz vzniká v prostoru za zrcadlem, je virtuální. Podle (10.84) je b >0 , obraz je vzpřímený. Pro dutá zrcadla (R<0) pro
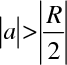 je
je
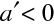 , a
, a
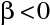 , tedy obraz vzniká v prostoru před zrcadlem, je tedy reálný, a je převrácený. Pro dutá zrcadla pro
, tedy obraz vzniká v prostoru před zrcadlem, je tedy reálný, a je převrácený. Pro dutá zrcadla pro
 je
je
 , a
, a
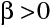 , což znamená, že obraz je virtuální a vzpřímený. K uvedeným závěrům lze dospět také pomocí geometrické konstrukce, v případě zrcadel obzvlášť jednoduché (použití dvou speciálních paprsků vycházejících z bodu předmětu: jeden paprsek procházející (eventuálně v prodloužení za zrcadlo) středem poloměru křivosti zrcadla zachovává při odrazu svůj směr, druhý paprsek procházející ohniskem se šíří po odrazu rovnoběžně s osou).
, což znamená, že obraz je virtuální a vzpřímený. K uvedeným závěrům lze dospět také pomocí geometrické konstrukce, v případě zrcadel obzvlášť jednoduché (použití dvou speciálních paprsků vycházejících z bodu předmětu: jeden paprsek procházející (eventuálně v prodloužení za zrcadlo) středem poloměru křivosti zrcadla zachovává při odrazu svůj směr, druhý paprsek procházející ohniskem se šíří po odrazu rovnoběžně s osou).
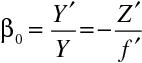 resp.
resp.
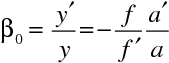
 . Úhlové zvětšení je definováno (
. Úhlové zvětšení je definováno (
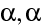 jsou úhly, které svírá paprsek s osou z) jako
jsou úhly, které svírá paprsek s osou z) jako
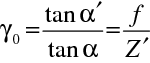 resp.
resp.
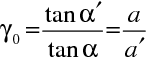
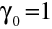 .V případě, kdy
.V případě, kdy
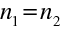 , tedy, kdy je například před čočkou i za čočkou prostředí se stejným indexem lomu, uzlové a hlavní body splývají, jak plyne přímo z rov. (10.70), (10.85) a (10.86).
Podélné zvětšení je definováno
, tedy, kdy je například před čočkou i za čočkou prostředí se stejným indexem lomu, uzlové a hlavní body splývají, jak plyne přímo z rov. (10.70), (10.85) a (10.86).
Podélné zvětšení je definováno
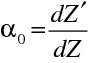
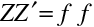 dostaneme
dostaneme

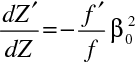
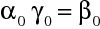
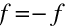 pak platí
pak platí
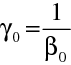
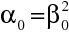

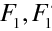 a ohniskovými vzdálenostmi
a ohniskovými vzdálenostmi
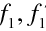 , druhý prvek má ohniskové body
, druhý prvek má ohniskové body
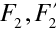 a vzdálenosti
a vzdálenosti
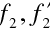 . Předpokládáme, že oba prvky jsou umístěny tak, aby jejich optické osy splývaly. Vzdálenost mezi oběma prvky se obvykle vyjadřuje pomocí optického intervalu
. Předpokládáme, že oba prvky jsou umístěny tak, aby jejich optické osy splývaly. Vzdálenost mezi oběma prvky se obvykle vyjadřuje pomocí optického intervalu
 , tedy vzdálenosti měřené od obrazového ohniska
, tedy vzdálenosti měřené od obrazového ohniska
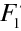 prvního prvku k předmětovému ohnisku
prvního prvku k předmětovému ohnisku
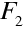 druhého prvku. Uvažujme nyní předmět znázorněný šipkou, jejíž koncový bod má v předmětovém prostoru prvního prvku souřadnice
druhého prvku. Uvažujme nyní předmět znázorněný šipkou, jejíž koncový bod má v předmětovém prostoru prvního prvku souřadnice
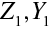 . První prvek vytvoří obraz, který má v jeho obrazovém prostoru souřadnice
. První prvek vytvoří obraz, který má v jeho obrazovém prostoru souřadnice
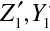 . Obrazový prostor prvního prvku je ovšem současně předmětovým prostorem prvku druhého, souřadnice předmětu pro druhý zobrazovací prvek jsou
. Obrazový prostor prvního prvku je ovšem současně předmětovým prostorem prvku druhého, souřadnice předmětu pro druhý zobrazovací prvek jsou
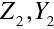 . Souřadnice výsledného obrazu v obrazovém prostoru druhého prvku jsou
. Souřadnice výsledného obrazu v obrazovém prostoru druhého prvku jsou
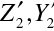 . Podle obrázku zřejmě platí
. Podle obrázku zřejmě platí
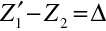
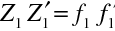
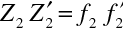
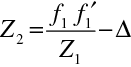

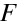 (souřadnice v soustavě spojené s obrazovým ohniskem
(souřadnice v soustavě spojené s obrazovým ohniskem
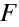 ) dostaneme z (10.97) v limitě
) dostaneme z (10.97) v limitě
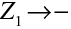
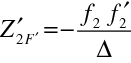
 máme pro polohu předmětového ohniska
máme pro polohu předmětového ohniska
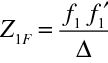
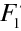 . Tento prvotní obraz je dále zobrazován druhou čočkou, podle Newtonova vztahu (10.76) dostaneme výsledek (10.98), uvážíme-li, že
. Tento prvotní obraz je dále zobrazován druhou čočkou, podle Newtonova vztahu (10.76) dostaneme výsledek (10.98), uvážíme-li, že
 . Odtud je zřejmé, proč ve vztahu (10.98) nevystupuje ohnisková vzdálenost první čočky. Podobnou úvahu můžeme provést i pro předmětové ohnisko.
. Odtud je zřejmé, proč ve vztahu (10.98) nevystupuje ohnisková vzdálenost první čočky. Podobnou úvahu můžeme provést i pro předmětové ohnisko.
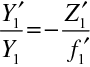
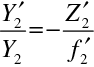
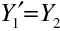 . Vydělením rovnic (10.100) a (10.101) a dosazením z (10.94) resp. (10.97) dostaneme pro příčné zvětšení celé soustavy
. Vydělením rovnic (10.100) a (10.101) a dosazením z (10.94) resp. (10.97) dostaneme pro příčné zvětšení celé soustavy
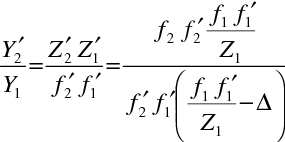
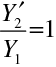 , která hlavní body definuje:
, která hlavní body definuje:
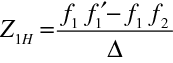
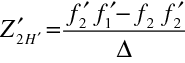
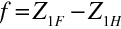
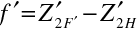
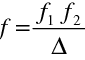
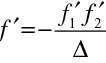
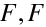 , můžeme přímo ukázat, že pro výsledné zobrazení platí obecné Newtonovy zobrazovací vztahy (10.76, 10.78).
, můžeme přímo ukázat, že pro výsledné zobrazení platí obecné Newtonovy zobrazovací vztahy (10.76, 10.78).

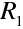 a
a
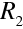 , které oddělují prostředí s indexy lomu postupně
, které oddělují prostředí s indexy lomu postupně
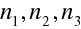 . Osou zobrazovací soustavy je přímka spojující středy křivosti obou ploch. Tloušťka čočky t je kladná geometrická vzdálenost vrcholů obou ploch. Tloušťka čočky je spojena s optickým intervalem a ohniskovými vzdálenostmi obou lámavých ploch, jak je zřejmé z obrázku
. Osou zobrazovací soustavy je přímka spojující středy křivosti obou ploch. Tloušťka čočky t je kladná geometrická vzdálenost vrcholů obou ploch. Tloušťka čočky je spojena s optickým intervalem a ohniskovými vzdálenostmi obou lámavých ploch, jak je zřejmé z obrázku
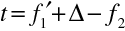 . Užíváme zde, stejně jako všude v této kapitole, znaménkovou konvenci. Pro ohniskové vzdálenosti obou lámavých ploch platí
. Užíváme zde, stejně jako všude v této kapitole, znaménkovou konvenci. Pro ohniskové vzdálenosti obou lámavých ploch platí
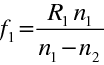
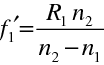
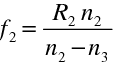
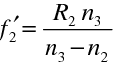
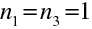 dostaneme pro výslednou ohniskovou vzdálenost
dostaneme pro výslednou ohniskovou vzdálenost
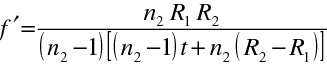
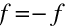
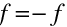 . V tomto případě se mluví o tenké čočce, na rozdíl od případu čočky tlusté. Tenká čočka je zřejmě aproximací, která se však velmi často používá pro jednoduchost výrazů. V aproximaci tenké čočky ve vzduchu můžeme psát výraz pro obrazovou ohniskovou vzdálenost ve tvaru
. V tomto případě se mluví o tenké čočce, na rozdíl od případu čočky tlusté. Tenká čočka je zřejmě aproximací, která se však velmi často používá pro jednoduchost výrazů. V aproximaci tenké čočky ve vzduchu můžeme psát výraz pro obrazovou ohniskovou vzdálenost ve tvaru
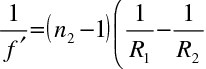
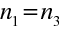 platí
platí
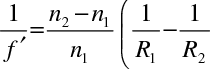
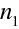 určuje pomocí optické mohutnosti , která se definuje
určuje pomocí optické mohutnosti , která se definuje
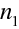
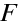 od vrcholu druhé lámavé plochy rovna
od vrcholu druhé lámavé plochy rovna
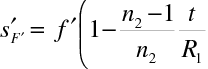
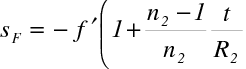
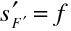 a
a
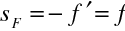 , což odpovídá tomu, že hlavní body leží pro tenkou čočku ve vrcholech obou sférických ploch, které splývají.
, což odpovídá tomu, že hlavní body leží pro tenkou čočku ve vrcholech obou sférických ploch, které splývají.