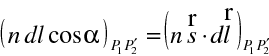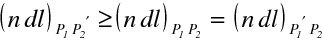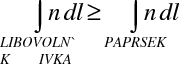3.1 Úvod do geometrické optiky
3.1.1 Eikonálová rovnice
Geometrická optika popisuje šíření světla pomocí paprsků světla. Paprsek světla intuitivně dobře chápeme, geometrická optika patří k nejstarším odvětvím fyziky. Lze paprsek zavést přesněji? V tomto odstavci ukážeme, že geometrickou optiku lze chápat jako limitní případ optiky "fyzikální", tedy vlnové, v případě, že délka vlny je velmi malá, tedy symbolicky pro
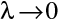 .
.
Uvažujme světelné pole, které popíšeme vektorem elektrické intenzity
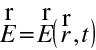 . V komplexní symbolice máme pro speciální případ harmonické rovinné vlny faktor popisující šíření vlny ("náběh fáze šířením") ve tvaru
. V komplexní symbolice máme pro speciální případ harmonické rovinné vlny faktor popisující šíření vlny ("náběh fáze šířením") ve tvaru
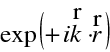 , kde
, kde
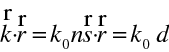 . Zde n je index lomu (homogenního, izotropního) prostředí, a d je optická dráha světla. Uvažujme nyní šíření světla v izotropním prostředí, které není již opticky homogenní, tedy
. Zde n je index lomu (homogenního, izotropního) prostředí, a d je optická dráha světla. Uvažujme nyní šíření světla v izotropním prostředí, které není již opticky homogenní, tedy
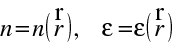 |
(10.1) |
Budeme vyšetřovat šíření harmonické vlny s obecnějším prostorovým charakterem ve tvaru, který vychází z výrazu pro rovinnou vlnu:
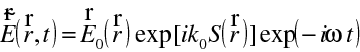 |
(10.2) |
Zde
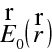 je amplituda pole, která se mění "pomalu" na vzdálenosti odpovídající vlnové délce (přesněji viz dále). Zavedená skalární funkce souřadnic
je amplituda pole, která se mění "pomalu" na vzdálenosti odpovídající vlnové délce (přesněji viz dále). Zavedená skalární funkce souřadnic
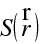 se nazývá eikonálem, podle řeckého εικών (obraz). Analogicky popíšeme magnetickou intenzitu,
se nazývá eikonálem, podle řeckého εικών (obraz). Analogicky popíšeme magnetickou intenzitu,
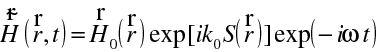 |
(10.3) |
Budeme zde předpokládat, že amplitudy
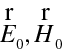 elektrického a magnetického pole jsou reálné (vhodná volba časového počátku). Za určitých přiblížení, která vymezují geometrickou optiku, můžeme z Maxwellových rovnic odvodit diferenciální rovnici pro eikonál S, v níž nebudou vystupovat amplitudy polí, která jednoznačně popisuje šíření vlny bez ohledu na její intenzitu.
elektrického a magnetického pole jsou reálné (vhodná volba časového počátku). Za určitých přiblížení, která vymezují geometrickou optiku, můžeme z Maxwellových rovnic odvodit diferenciální rovnici pro eikonál S, v níž nebudou vystupovat amplitudy polí, která jednoznačně popisuje šíření vlny bez ohledu na její intenzitu.
Do "rotačních" Maxwellových rovnic, rov. (1.1, 1.2), pro případ dielektrika (
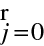 )
)
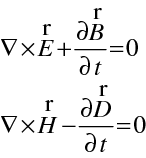 |
(10.4) |
dosadíme za intenzity pole z (10.2) a (10.3). Budeme uvažovat materiálové vztahy
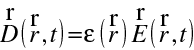 |
(10.5) |
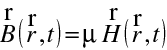 .
.
 (10.6)
Použijeme dále vztah pro rotaci součinu vektoru a skaláru
(10.6)
Použijeme dále vztah pro rotaci součinu vektoru a skaláru
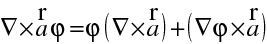 |
(10.7) |
Tak z rovnice pro rotaci magnetické intenzity dostáváme
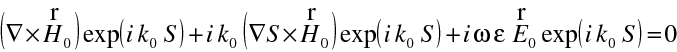 |
(10.8) |
V posledním členu je podle definice velikosti vlnového vektoru
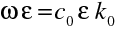 |
(10.9) |
Z (10.8) máme
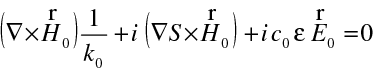 |
(10.10) |
V limitě
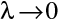 , je
, je
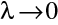 , a první člen v rovnici (10.10) můžeme zanedbat. Ve skutečnosti je
, a první člen v rovnici (10.10) můžeme zanedbat. Ve skutečnosti je
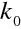 velké, například pro vlnovou délku 550 nm (zelené světlo) je
velké, například pro vlnovou délku 550 nm (zelené světlo) je
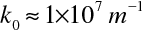 . Rotace amplitudy vektoru
. Rotace amplitudy vektoru
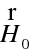 vynásobená
vynásobená
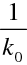 obsahuje členy typu
obsahuje členy typu
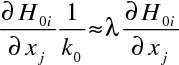 |
(10.11) |
Tyto členy je možné zanedbat, pokud budou velmi malé, tedy pokud bude amplituda pole taková, že její změna na vzdálenostech odpovídající vlnové délce bude zanedbatelná.
Rovnice (10.10) v limitě přejde na tvar
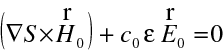 |
(10.12) |
Zcela analogicky můžeme z "rotační" rovnice pro intenzitu elektrického pole odvodit rovnici
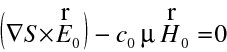 |
(10.13) |
Z (10.13) lze vyjádřit explicitně
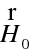 :
:
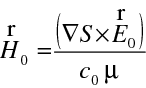 |
(10.14) |
a dosadit do (10.12). Získáme tak
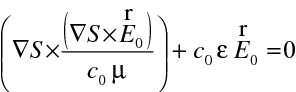 |
(10.15) |
Využijeme-li výraz pro vektorový součin
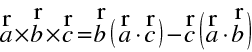 , máme
, máme
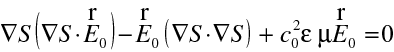 . (10.16) Ovšem pro amplitudu elektrického pole máme z (10.12)
. (10.16) Ovšem pro amplitudu elektrického pole máme z (10.12)
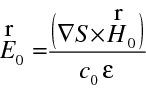 |
(10.17) |
Odtud zřejmě plyne
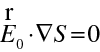 |
(10.18) |
a tedy první člen v (10.16) je roven vždy nule. Z (10.16) tedy máme
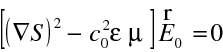 (10.19) a pro nenulové pole
(10.19) a pro nenulové pole
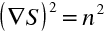 |
(10.20) |
Využili jsme zde vztahu
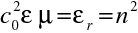 |
(10.21) |
Rovnice (10.20) se nazývá eikonálová rovnice.
Ve složkách má tvar
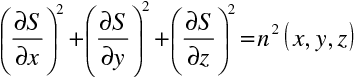 |
(10.22) |
Geometrické místo bodů s konstantní hodnotou eikonálu
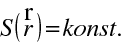 |
(10.23) |
určuje vlnoplochu (ve smyslu geometrické optiky). Paprsek, který je velmi dobře intuitivně chápán, můžeme nyní definovat přesně jako normálu k vlnoploše. Jednotkový paprskový vektor je tedy určen (jak je zřejmé z (10.20))
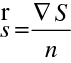 |
(10.24) |
Z rovnic (10.14) a (10.17) plyne, že amplitudové vektory
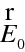 ,
,
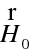 jsou kolmé na směr paprsku (i navzájem), což odpovídá případu rovinné vlny, světlo má tedy v případě geometrické optiky lokálně charakter rovinné vlny.
jsou kolmé na směr paprsku (i navzájem), což odpovídá případu rovinné vlny, světlo má tedy v případě geometrické optiky lokálně charakter rovinné vlny.
3.1.2 Zákon lomu pro paprsky
Nyní si všimneme vlastností vektoru (
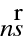 ). Rotace tohoto vektoru je rovna nule, jak plyne přímo z (10.24)
). Rotace tohoto vektoru je rovna nule, jak plyne přímo z (10.24)
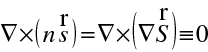 |
(10.25) |
To ovšem podle Stokesovy věty (vektorová analýza) znamená, že také cirkulace uvedeného vektoru po uzavřené křivce je nulová,
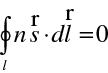 |
(10.26) |
Poslední rovnice se nazývá Lagrangeovým invariantem. Můžeme ji využít pro odvození zákona lomu pro paprsek. Uvažujme rozhraní oddělující dvě optická prostředí s indexy lomu
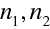 . Počítáme-li cirkulaci (10.26) po obvodu obdélníka jako na obr. 10.1 máme v limitě, kdy výšku obdélníka "stáhneme" k rozhraní (ve skalárním součinu ve (10.26) je kosinus doplňkových úhlů k q 1 , q 2 ),
. Počítáme-li cirkulaci (10.26) po obvodu obdélníka jako na obr. 10.1 máme v limitě, kdy výšku obdélníka "stáhneme" k rozhraní (ve skalárním součinu ve (10.26) je kosinus doplňkových úhlů k q 1 , q 2 ),
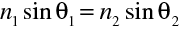 |
(10.27) |
tedy zákon lomu pro paprsek. Ten je ovšem základním vztahem geometrické optiky1.
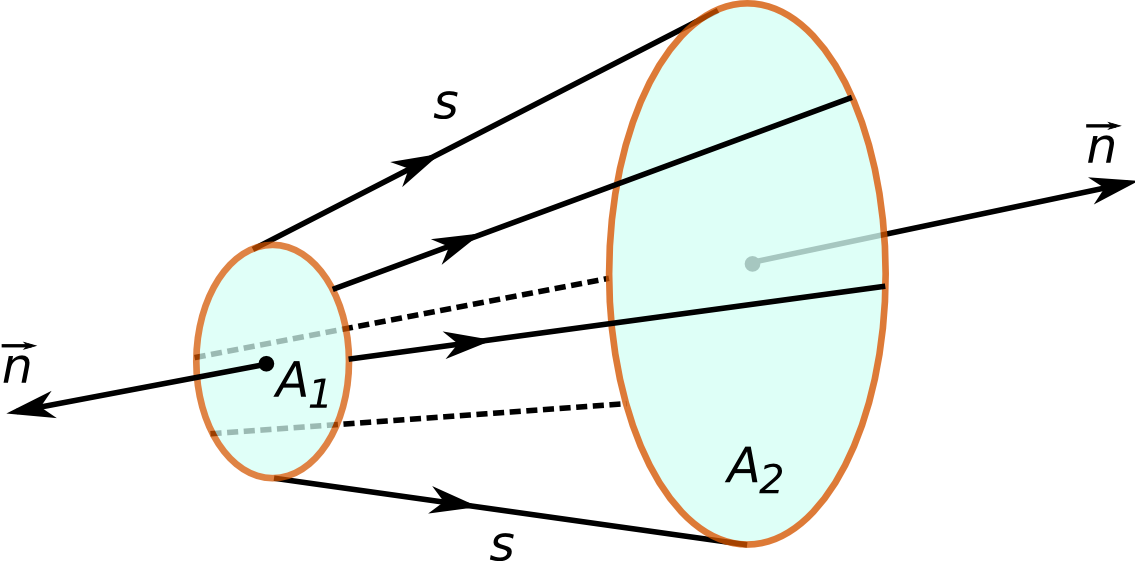 Obr. 10.1
Obr. 10.1 Schéma k odvození zákona lomu pro paprsky
3.1.3 Intenzita světla v geometrické optice
Intenzita světla je rovna časové střední hodnotě velikosti Poyntingova vektoru (viz rov. (1.69)), tedy
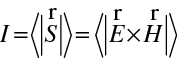 |
(10.28) |
V uvažovaném tvaru vln (amplitudy jsou reálné), můžeme psát
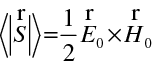 |
(10.29) |
Dosadíme-li za
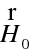 z (10.14), dostaneme
z (10.14), dostaneme
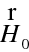 |
(10.30) |
použijeme-li výraz pro trojný vektorový součin a uvážíme-li, že platí (10.18) (v (10.30) se projevuje poněkud nešťastné označení eikonálu a Poyntingova vektoru stejným písmenem)
Do výrazu pro intenzitu můžeme dosadit paprskový vektor (10.24), pak
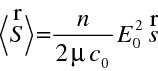 |
(10.31) |
tedy
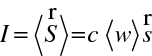 |
(10.32) |
kde
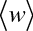 je časová střední hodnota elektromagnetické hustoty energie. Vztah (10.32) je stejný jako v případě rovinné vlny. Z Poyntingovy věty pro časově neproměnnou hustotu energie plyne
je časová střední hodnota elektromagnetické hustoty energie. Vztah (10.32) je stejný jako v případě rovinné vlny. Z Poyntingovy věty pro časově neproměnnou hustotu energie plyne
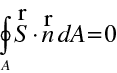 |
(10.33) |
což je plošný integrál Poyntingova vektoru přes uzavřenou plochu A. Použijeme nyní tento vztah pro situaci na obr. 10.2, tj. na plochu tvořenou částmi ("podstavami")
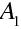 , resp.
, resp.
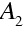 , které jsou kolmé na paprsky a částí, která je tvořena paprsky ("plášť").
, které jsou kolmé na paprsky a částí, která je tvořena paprsky ("plášť").
 Obr. 10.2
Obr. 10.2 Intenzita světla v geometrické optice
Integrál přes plášť je roven nule vzhledem ke směru toku energie. Pokud jsou plochy malé, přejde integrál na násobení, je nutné uvážit směry normál k plochám. Po provedení časového středování dostaneme zákon změny intenzity pro geometrickou optiku, tj.
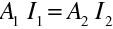 |
(10.34) |
3.1.4 Paprsková rovnice
Kromě eikonálové rovnice je výhodné zformulovat rovnici, která by popisovala přímo paprsek, tedy paprskovou rovnici. Pokud určitý bod paprsku - viz obr. 10.3 - má polohový vektor
 , změní se při posunu o délku
, změní se při posunu o délku
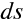 po paprsku polohový vektor o
po paprsku polohový vektor o
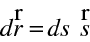 |
(10.35) |
Pro polohový vektor jako funkci délky paprsku s tedy máme
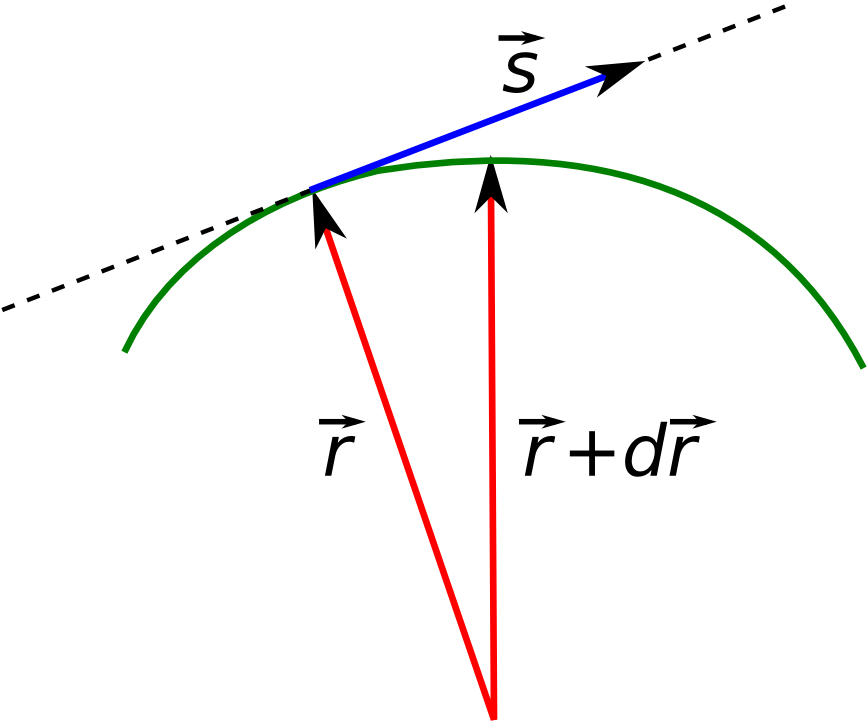 Obr. 10.3
Obr. 10.3 Schéma k odvození paprskové rovnice
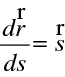 |
(10.36) |
Po vynásobení obou stran rovnice (10.36) (prostorově závislým) indexem lomu a derivování podle s, tedy ve směru
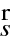 (podle paprsku), dostaneme
(podle paprsku), dostaneme
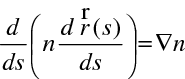 |
(10.37) |
což je paprsková rovnice. Platnost vektorové rovnice (10.37) ukážeme ve složkách. Například x-ovou složku levé strany (10.37) můžeme podle (10.36) a podle definice derivace ve směru (pro jednoduchost označíme
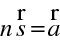 ) formálně přepsat
) formálně přepsat
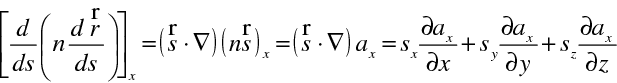 |
(10.38) |
 Protože podle (10.25) je
Protože podle (10.25) je
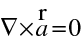 , jak plyne z eikonálové rovnice, platí pro parciální derivace komponent aj
, jak plyne z eikonálové rovnice, platí pro parciální derivace komponent aj
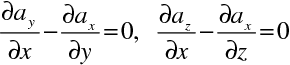 |
(10.39) |
Vztah (10.38) můžeme podle (10.39) (
 je jednotkový vektor) upravit
je jednotkový vektor) upravit
 |
(10.40) |
což je již paprsková rovnice (10.37) pro x-ovou složku.
Vyřešením paprskové rovnice pro danou závislost
 dostaneme dráhu paprsku, tedy
dostaneme dráhu paprsku, tedy
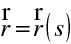 . Jako příklad můžeme uvést šíření v prostředí s konstantním indexem lomu. Pak bude mít paprsková rovnice jednoduchý tvar
. Jako příklad můžeme uvést šíření v prostředí s konstantním indexem lomu. Pak bude mít paprsková rovnice jednoduchý tvar
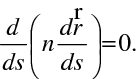 |
(10.41) |
Její řešení je
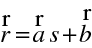 |
(10.42) |
kde
 a
a
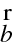 jsou konstantní vektory. V tomto případě se tedy šíří světlo po přímce, přímočaře. Rovnici můžeme ovšem použít k výpočtům i v obecném případě proměnného indexu lomu, kdy paprsky mohou být složité křivky.
10.1.5 Fermatův princip
jsou konstantní vektory. V tomto případě se tedy šíří světlo po přímce, přímočaře. Rovnici můžeme ovšem použít k výpočtům i v obecném případě proměnného indexu lomu, kdy paprsky mohou být složité křivky.
10.1.5 Fermatův princip
Nyní ukážeme, že platí Fermatův princip, který je často považován za základní východisko geometrické optiky (Pierre de Fermat, 1662). Uvažujme paprsky jako na obr. 10.4, dva blízké paprsky například procházejí mezi body
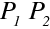 , respektive
, respektive
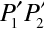 . V jejich blízkém okolí uvažujme libovolnou křivku
. V jejich blízkém okolí uvažujme libovolnou křivku
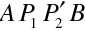 .
.
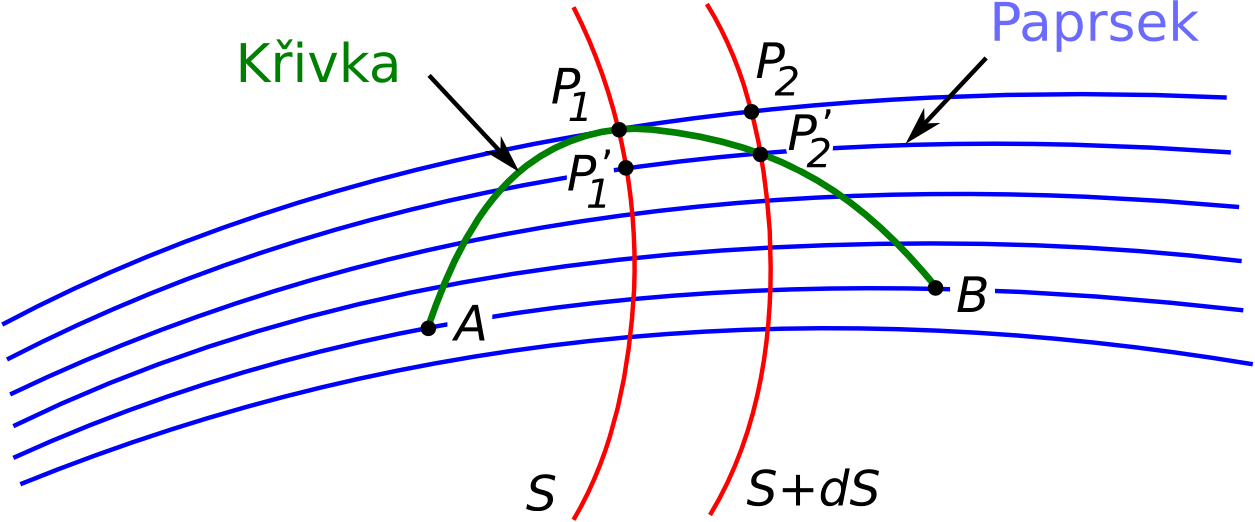 Obr. 10.4
Obr. 10.4 K výkladu Fermatova principu
Jsou zde také zakresleny dvě blízké plochy konstantního eikonálu s hodnotami S a S + dS. Podle vztahu (10.26) platí
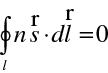 . Počítáme-li cirkulaci po křivce tvořené malými úseky
. Počítáme-li cirkulaci po křivce tvořené malými úseky
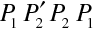 , máme
, máme
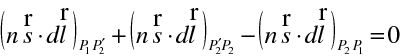 |
(10.43) |
 Poslední člen představuje část cirkulace po paprsku. Prostřední člen odpovídající úseku
Poslední člen představuje část cirkulace po paprsku. Prostřední člen odpovídající úseku
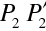 je roven nule,
je roven nule,
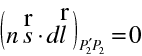 |
(10.44) |
protože je zřejmě podle (10.24) vektor
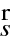 kolmý k ploše konstantního eikonálu, po níž se integruje. Pro optickou délku úseku křivky
kolmý k ploše konstantního eikonálu, po níž se integruje. Pro optickou délku úseku křivky
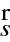 platí zřejmě
platí zřejmě
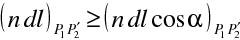 |
(10.45) |
pro libovolný úhel
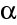 . Je-li to úhel mezi vektory
. Je-li to úhel mezi vektory
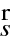 a
a
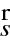 , je
, je
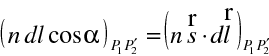 |
(10.46) |
Z rov. (10.43 až 46) plyne
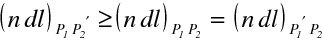 |
(10.47) |
poslední rovnost platí, protože se jedná o velikosti optické dráhy po paprscích mezi plochami stejného eikonálu. Nerovnost (10.47) znamená, že délka optické dráhy po úseku libovolné křivky je větší než délka optické dráhy po odpovídajícím úseku paprsku. Uvedený postup můžeme opakovat pro další úseky zvolené křivky AB. Odtud tedy plyne závěr, že optická dráha po (libovolné) křivce AB je větší než optická dráha po paprsku. To je jedna z formulací Fermatova principu:
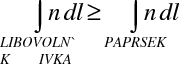 |
(10.48) |
Světlo se tedy šíří tak, že délka optické dráhy po paprsku je kratší než délky optických drah po libovolných jiných křivkách, které leží v okolí paprsku. Doba šíření světla je rovna podílu délky optické dráhy a rychlosti světla ve vakuu. Fermatův princip bývá proto také často formulován jako princip nejkratšího času, tedy, že světlo se šíří mezi dvěma body tak, aby doba šíření byla co nejkratší. Takto ho také Fermat původně (1891) vyslovil. Obecněji je ovšem možné ho formulovat tak, že optická dráha mezi dvěma body, kterými prochází světelný paprsek, je extremální (tj. musí být minimální, maximální nebo musí odpovídat inflexnímu bodu). Řečeno jinak, variace dráhy musí být nulová. Princip se vztahuje na křivky v blízkém okolí, nemusí jít o globální extrém.
 .
.
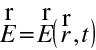 . V komplexní symbolice máme pro speciální případ harmonické rovinné vlny faktor popisující šíření vlny ("náběh fáze šířením") ve tvaru
. V komplexní symbolice máme pro speciální případ harmonické rovinné vlny faktor popisující šíření vlny ("náběh fáze šířením") ve tvaru
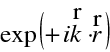 , kde
, kde
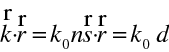 . Zde n je index lomu (homogenního, izotropního) prostředí, a d je optická dráha světla. Uvažujme nyní šíření světla v izotropním prostředí, které není již opticky homogenní, tedy
. Zde n je index lomu (homogenního, izotropního) prostředí, a d je optická dráha světla. Uvažujme nyní šíření světla v izotropním prostředí, které není již opticky homogenní, tedy
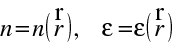
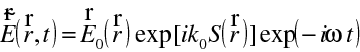
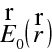 je amplituda pole, která se mění "pomalu" na vzdálenosti odpovídající vlnové délce (přesněji viz dále). Zavedená skalární funkce souřadnic
je amplituda pole, která se mění "pomalu" na vzdálenosti odpovídající vlnové délce (přesněji viz dále). Zavedená skalární funkce souřadnic
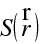 se nazývá eikonálem, podle řeckého εικών (obraz). Analogicky popíšeme magnetickou intenzitu,
se nazývá eikonálem, podle řeckého εικών (obraz). Analogicky popíšeme magnetickou intenzitu,
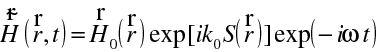
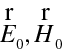 elektrického a magnetického pole jsou reálné (vhodná volba časového počátku). Za určitých přiblížení, která vymezují geometrickou optiku, můžeme z Maxwellových rovnic odvodit diferenciální rovnici pro eikonál S, v níž nebudou vystupovat amplitudy polí, která jednoznačně popisuje šíření vlny bez ohledu na její intenzitu.
elektrického a magnetického pole jsou reálné (vhodná volba časového počátku). Za určitých přiblížení, která vymezují geometrickou optiku, můžeme z Maxwellových rovnic odvodit diferenciální rovnici pro eikonál S, v níž nebudou vystupovat amplitudy polí, která jednoznačně popisuje šíření vlny bez ohledu na její intenzitu.
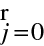 )
)

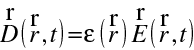
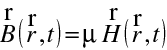 .
.
 (10.6)
Použijeme dále vztah pro rotaci součinu vektoru a skaláru
(10.6)
Použijeme dále vztah pro rotaci součinu vektoru a skaláru
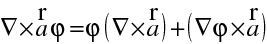
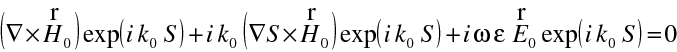
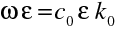
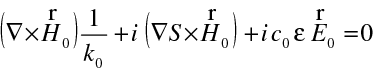
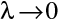 , je
, je
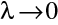 , a první člen v rovnici (10.10) můžeme zanedbat. Ve skutečnosti je
, a první člen v rovnici (10.10) můžeme zanedbat. Ve skutečnosti je
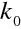 velké, například pro vlnovou délku 550 nm (zelené světlo) je
velké, například pro vlnovou délku 550 nm (zelené světlo) je
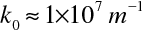 . Rotace amplitudy vektoru
. Rotace amplitudy vektoru
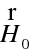 vynásobená
vynásobená
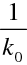 obsahuje členy typu
obsahuje členy typu
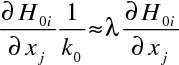
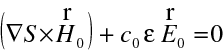
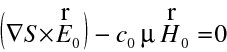
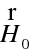 :
:
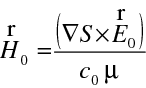
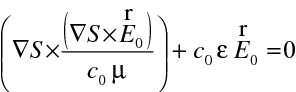
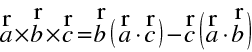 , máme
, máme
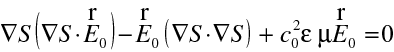 . (10.16) Ovšem pro amplitudu elektrického pole máme z (10.12)
. (10.16) Ovšem pro amplitudu elektrického pole máme z (10.12)
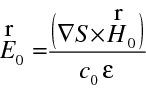
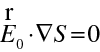
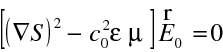 (10.19) a pro nenulové pole
(10.19) a pro nenulové pole
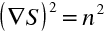
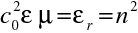
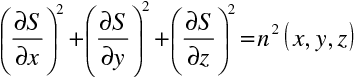
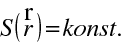
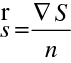
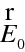 ,
,
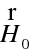 jsou kolmé na směr paprsku (i navzájem), což odpovídá případu rovinné vlny, světlo má tedy v případě geometrické optiky lokálně charakter rovinné vlny.
jsou kolmé na směr paprsku (i navzájem), což odpovídá případu rovinné vlny, světlo má tedy v případě geometrické optiky lokálně charakter rovinné vlny.
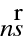 ). Rotace tohoto vektoru je rovna nule, jak plyne přímo z (10.24)
). Rotace tohoto vektoru je rovna nule, jak plyne přímo z (10.24)
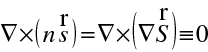
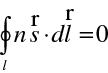
 . Počítáme-li cirkulaci (10.26) po obvodu obdélníka jako na obr. 10.1 máme v limitě, kdy výšku obdélníka "stáhneme" k rozhraní (ve skalárním součinu ve (10.26) je kosinus doplňkových úhlů k q 1 , q 2 ),
. Počítáme-li cirkulaci (10.26) po obvodu obdélníka jako na obr. 10.1 máme v limitě, kdy výšku obdélníka "stáhneme" k rozhraní (ve skalárním součinu ve (10.26) je kosinus doplňkových úhlů k q 1 , q 2 ),
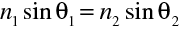

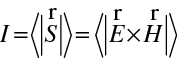
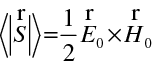
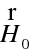 z (10.14), dostaneme
z (10.14), dostaneme
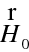
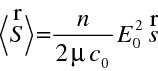
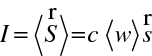
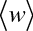 je časová střední hodnota elektromagnetické hustoty energie. Vztah (10.32) je stejný jako v případě rovinné vlny. Z Poyntingovy věty pro časově neproměnnou hustotu energie plyne
je časová střední hodnota elektromagnetické hustoty energie. Vztah (10.32) je stejný jako v případě rovinné vlny. Z Poyntingovy věty pro časově neproměnnou hustotu energie plyne
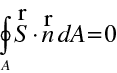
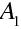 , resp.
, resp.
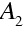 , které jsou kolmé na paprsky a částí, která je tvořena paprsky ("plášť").
, které jsou kolmé na paprsky a částí, která je tvořena paprsky ("plášť").

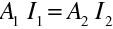
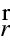 , změní se při posunu o délku
, změní se při posunu o délku
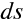 po paprsku polohový vektor o
po paprsku polohový vektor o
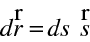

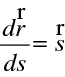
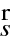 (podle paprsku), dostaneme
(podle paprsku), dostaneme
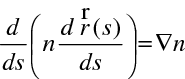
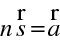 ) formálně přepsat
) formálně přepsat
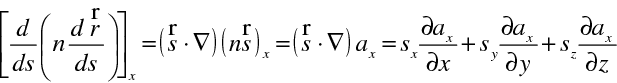
 Protože podle (10.25) je
Protože podle (10.25) je
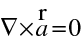 , jak plyne z eikonálové rovnice, platí pro parciální derivace komponent aj
, jak plyne z eikonálové rovnice, platí pro parciální derivace komponent aj
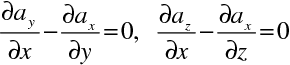
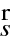 je jednotkový vektor) upravit
je jednotkový vektor) upravit
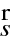
 dostaneme dráhu paprsku, tedy
dostaneme dráhu paprsku, tedy
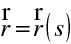 . Jako příklad můžeme uvést šíření v prostředí s konstantním indexem lomu. Pak bude mít paprsková rovnice jednoduchý tvar
. Jako příklad můžeme uvést šíření v prostředí s konstantním indexem lomu. Pak bude mít paprsková rovnice jednoduchý tvar
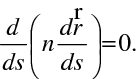
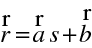
 a
a
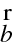 jsou konstantní vektory. V tomto případě se tedy šíří světlo po přímce, přímočaře. Rovnici můžeme ovšem použít k výpočtům i v obecném případě proměnného indexu lomu, kdy paprsky mohou být složité křivky.
10.1.5 Fermatův princip
jsou konstantní vektory. V tomto případě se tedy šíří světlo po přímce, přímočaře. Rovnici můžeme ovšem použít k výpočtům i v obecném případě proměnného indexu lomu, kdy paprsky mohou být složité křivky.
10.1.5 Fermatův princip
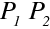 , respektive
, respektive
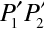 . V jejich blízkém okolí uvažujme libovolnou křivku
. V jejich blízkém okolí uvažujme libovolnou křivku
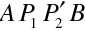 .
.

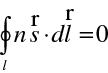 . Počítáme-li cirkulaci po křivce tvořené malými úseky
. Počítáme-li cirkulaci po křivce tvořené malými úseky
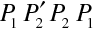 , máme
, máme
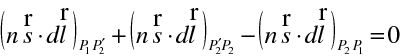
 Poslední člen představuje část cirkulace po paprsku. Prostřední člen odpovídající úseku
Poslední člen představuje část cirkulace po paprsku. Prostřední člen odpovídající úseku
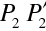 je roven nule,
je roven nule,
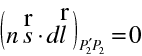
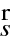 kolmý k ploše konstantního eikonálu, po níž se integruje. Pro optickou délku úseku křivky
kolmý k ploše konstantního eikonálu, po níž se integruje. Pro optickou délku úseku křivky
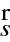 platí zřejmě
platí zřejmě
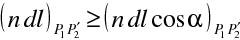
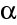 . Je-li to úhel mezi vektory
. Je-li to úhel mezi vektory
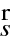 a
a
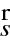 , je
, je