2 Interference světla
Z principu superpozice vyplývá, že pokud jednotlivá světelná pole jsou řešením vlnové rovnice, je řešením i jejich součet. Pokud se tedy v prostoru setkávají například dvě světelné vlny
,
, je výsledné pole dáno součtem
 |
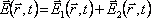(5.1) |
Okem a detektory však zaznamenáváme intenzitu světla. To ovšem znamená, že odpovídají-li zmíněným dvěma světelným polím intenzity
a
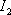, není obecně výsledná intenzita I rovna součtu jednotlivých intenzit,
. Ukazuje se naopak, že v určitých místech může být intenzita větší než součet, jinde menší nebo dokonce nulová. Jevy, v nichž skládání dvou nebo více polí vede k prostorové modulaci intenzity výsledného pole, se nazývají interferenčními jevy. Interference světla je tedy skládání světla. Protože výsledná modulace světelné intenzity je přímým důsledkem vlnové povahy světla, považovala se v historii vždy existence interference za přímý důkaz vlnové povahy světla.Slavný je zejména Youngův interferenční experiment, který popíšeme v dalších odstavcích.
Jakkoliv není z hlediska teoretického interference nic jiného než správné sčítání vektorů elektrické intenzity a pak výpočet intenzity světla, z hlediska optických jevů zahrnují interferenční jevy širokou škálu situací - od interferometrů pro spektrální měření přes laserové rezonátory až po barevné jevy na olejových skvrnách na vodě či barevná křídla motýlů. Proto stojí za jistou námahu vypsat sčítání polí v některých typických situacích explicitně.
V řadě praktických případů se ovšem interference neprojevuje. Například příspěvky světelných toků jednotlivých žárovek na lustru se jednoduše sčítají. V tomto případě se totiž nesčítají uspořádané monochromatické vlny, ale neuspořádané světlo s amplitudou nebo fázemi náhodně se měnícími v čase. Středování při výpočtu výsledné intenzity světla pak vede k nulové hodnotě interferenčního členu.
