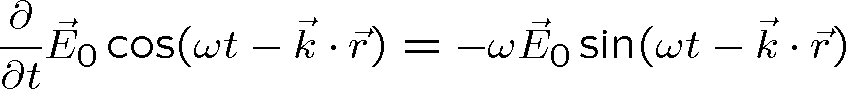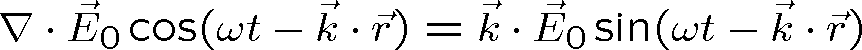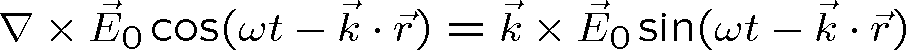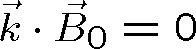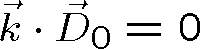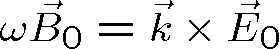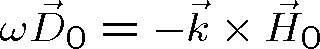1.3 Rovinné vlny
Každé řešení vlnové rovnice se nazývá vlnou. Rovnost druhých parciálních derivací podle času a souřadnic (až na druhou mocninu fázové rychlosti) vede k tomu, že v argumentu funkce, popisující vlnu, musí být čas a prostorová souřadnice spojeny do obecné fáze vlny. To odpovídá tomu, jak chápeme vlnu intuitivně: jedná se o rozruch, který se šíří v prostoru a čase. Nabude určité velikosti v určitém místě a čase, v jiném místě nabude stejné velikosti v jiném čase, až tam vlna dorazí. Geometrické místo bodů, v nichž má obecná fáze vlny pro určitý čas konstantní hodnotu, se nazývá vlnoplochou (plocha konstantní fáze). V optice hrají významnou roli vlny rovinné (vlnoplochy jsou roviny)a vlny kulové (sférické) (vlnoplochy jsou kulové plochy). Speciálním případem jsou pak vlny harmonické, které jsou popsány funkcí kosinus nebo sinus. Pokud je na vlnoploše konstantní hodnota amplitudy vlny, nazývá se vlna homogenní3. V případech, kdy je důležitá jen jedna kartézská složka elektrického nebo magnetického pole, je možné uvažovat jen vlnovou rovnici pro tuto složku. Řešení této skalární rovnice se nazývá skalární vlna. V optice se dává přednost elektrickému poli, protože při interakci světla s látkou hraje zpravidla dominantní roli (nejsilnější optické přechody v atomech jsou spojeny s jejich elektrickými dipólovými momenty).
1.3.1 Obecná rovinná světelná vlna
Rovinné elektromagnetické vlny4 jsou důležitým řešením vlnové rovnice. Budeme se zde zabývat homogenními rovinnými vlnami. V nich závisí elektrické a magnetické pole pouze na vzdálenosti měřené v určitém směru. Pokud vhodně natočíme souřadný systém tak, že tento význačný směr odpovídá směru osy z, znamená to, že vektory pole se stávají závislé pouze na jedné souřadnici, na z. Pak má ovšem vlnová rovnice pro libovolnou komponentu vektoru
 tvar
tvar
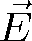 |
(1.17) |
Podobně platí tato jednodimensionální rovnice i pro pole B. Tuto rovnici je možné přepsat na tvar
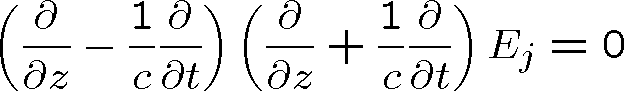 |
(1.18) |
Přejdeme-li k novým proměnným
 a
a

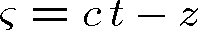 |
(1.19) |
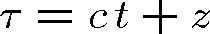 |
(1.20) |
máme
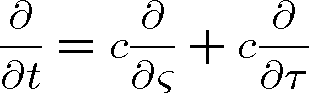 |
(1.21) |
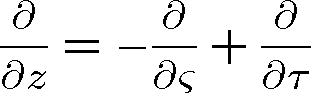 |
(1.22) |
Vlnová rovnice (1.17) má v nových proměnných tvar
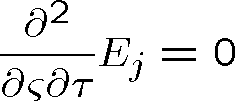 |
(1.23) |
Obecné řešení této rovnice je zřejmě
 |
(1.24) |
kde f1 , f2 jsou libovolné funkce. Dosadíme-li zpět původní proměnné, dostaneme
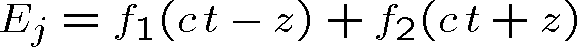 |
(1.25) |
Řešení má jasný smysl. Pro případ f2 =0 máme pro komponentu pole
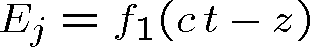 |
(1.26) |
V určité rovině
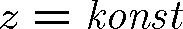 závisí pole jen na čase, v určitém časovém okamžiku závisí pole jen na souřadnici z. Pole bude mít zřejmě stejnou velikost pro všechny souřadnice a časy, které jsou spojeny výrazem
závisí pole jen na čase, v určitém časovém okamžiku závisí pole jen na souřadnici z. Pole bude mít zřejmě stejnou velikost pro všechny souřadnice a časy, které jsou spojeny výrazem
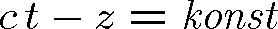 |
(1.27) |
Pokud například v čase t=0 a v rovině z=0 bude mít pole určitou hodnotu, bude v dalším čase nabývat této hodnoty v místech
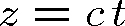 . Geometrické místo stejných hodnot pole, rovina, se tedy bude šířit rychlostí c v kladném směru osy z. Řešení f2 odpovídá rovinné vlně, která běží v záporném smyslu osy z. Pokud chceme vyjádřit rovinnou vlnu v obecném případě, kdy směr náběhu fáze, směr šíření, je určen jednotkovým vektorem
. Geometrické místo stejných hodnot pole, rovina, se tedy bude šířit rychlostí c v kladném směru osy z. Řešení f2 odpovídá rovinné vlně, která běží v záporném smyslu osy z. Pokud chceme vyjádřit rovinnou vlnu v obecném případě, kdy směr náběhu fáze, směr šíření, je určen jednotkovým vektorem
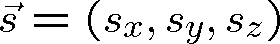 (viz obr. 1.2), bude argument rovinné vlny mít tvar (
(viz obr. 1.2), bude argument rovinné vlny mít tvar (
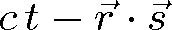 ), protože skalární součin
), protože skalární součin
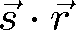 je roven průmětu libovolného polohového vektoru
je roven průmětu libovolného polohového vektoru
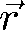 do směru
do směru
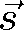 , odpovídá tedy výše uvažované souřadnici z. Tento argument se nazývá fází vlny. Elektrické a magnetické pole rovinné vlny má tedy jednotlivé komponenty, které závisí na fázi vyjádřené v uvedeném tvaru. Aby ovšem vektory elektrického a magnetického pole byly řešením Maxwellových rovnic, musí splňovat ještě další podmínky. Uvažujeme tedy vektory
, odpovídá tedy výše uvažované souřadnici z. Tento argument se nazývá fází vlny. Elektrické a magnetické pole rovinné vlny má tedy jednotlivé komponenty, které závisí na fázi vyjádřené v uvedeném tvaru. Aby ovšem vektory elektrického a magnetického pole byly řešením Maxwellových rovnic, musí splňovat ještě další podmínky. Uvažujeme tedy vektory
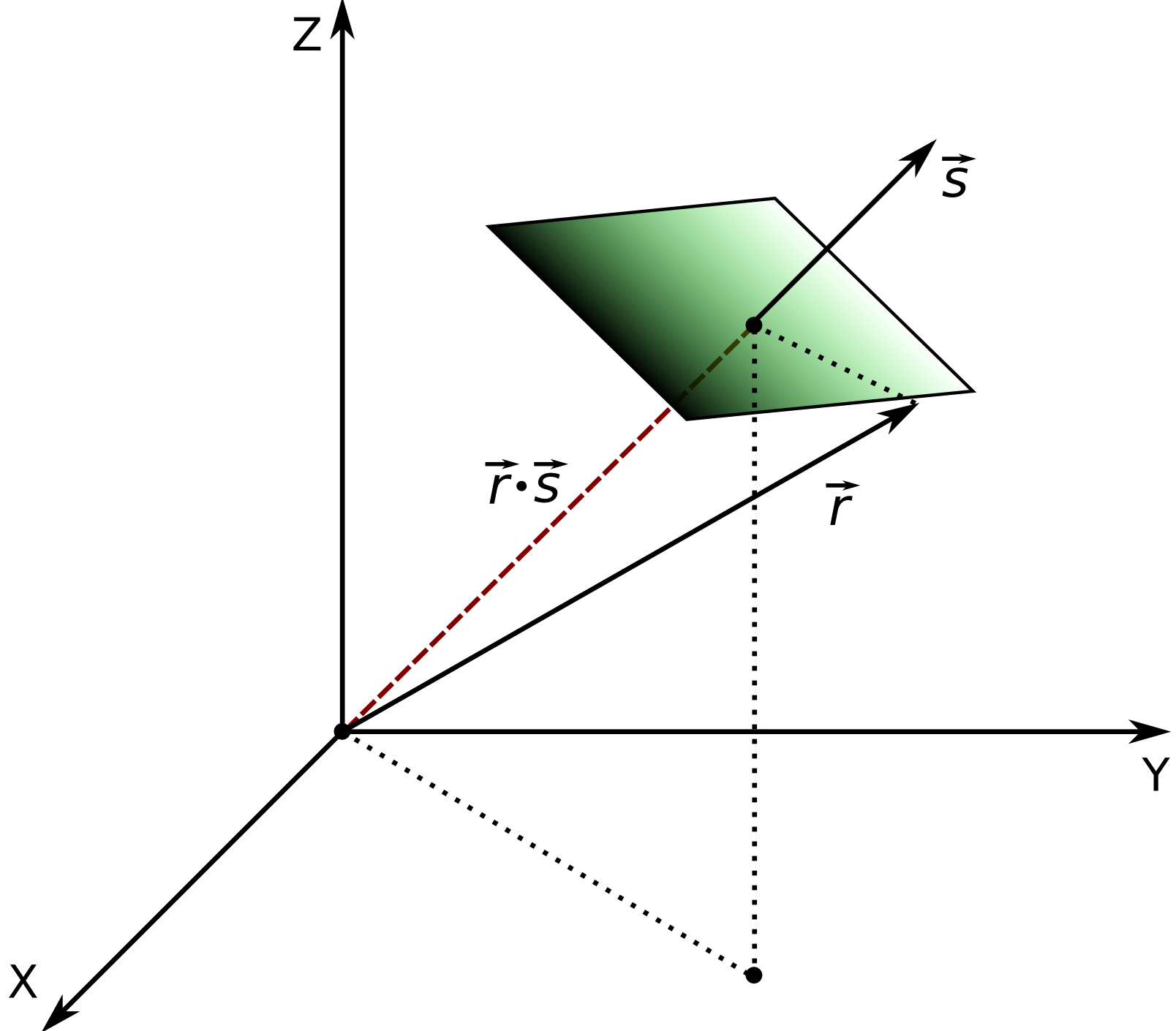 Obr. 1.2
Obr. 1.2 Šíření rovinné vlny v obecném směru, který je dán jednotkovým vektorem
s.
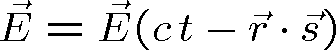 |
(1.28) |
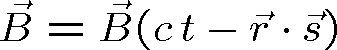 |
(1.29) |
Zřejmě pro derivace platí
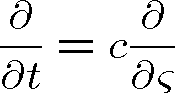 |
(1.30) |
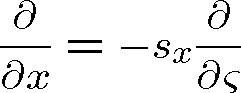 ,
,
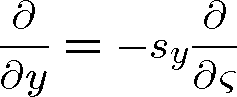 ,
,
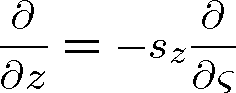 . (1.31)
Proto můžeme vyjádřit
. (1.31)
Proto můžeme vyjádřit
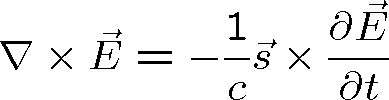 |
(1.32) |
a z rovnice (1.1) dostáváme
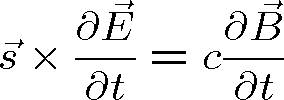 |
(1.33) |
Zcela stejně z rov. (1.2) máme
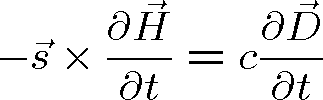 |
(1.34) |
Poslední dvě rovnice je možné integrovat podle času, přičemž integrační konstantu, která by znamenala konstantní hodnotu polí (ne časově proměnné vlnění) položíme rovnou nule. Pak dostaneme dvě rovnice, které spojují vektory
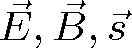
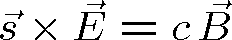 |
(1.35) |
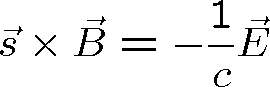 |
(1.36) |
Vztah (1.36) plyne z rov. (1.34) a z materiálových vztahů pro izotropní prostředí. Ze vztahů (1.35), (1.36) je zřejmé, že vektory
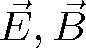 musí být kolmé na směr šíření (skutečně skalární součin
musí být kolmé na směr šíření (skutečně skalární součin
 i kolmé navzájem.5 Pro izotropní prostředí jsou ovšem vektory
i kolmé navzájem.5 Pro izotropní prostředí jsou ovšem vektory
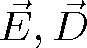 , resp.
, resp.
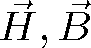 kolineární. Rovinné elektromagnetické vlny jsou tedy v izotropním prostředí příčné, vektory mají vzájemnou orientaci jak je znázorněno na obr. 1.3. Například z rov. (1.35)
kolineární. Rovinné elektromagnetické vlny jsou tedy v izotropním prostředí příčné, vektory mají vzájemnou orientaci jak je znázorněno na obr. 1.3. Například z rov. (1.35)
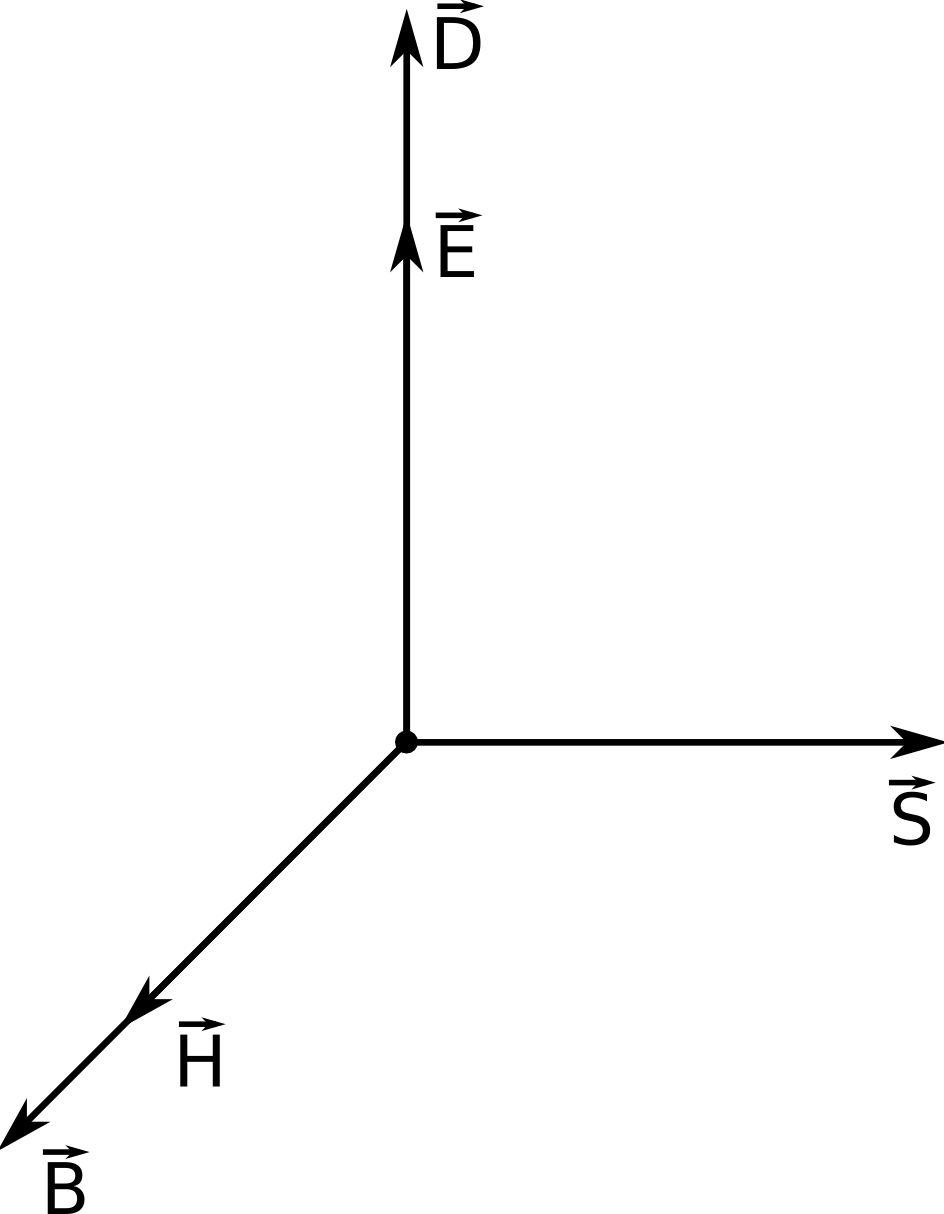 Obr. 1.3
Obr. 1.3 Vzájemná orientace vektorů elektrického a magnetického pole v rovinné vlně
vyplývá vztah mezi velikostmi navzájem kolmých vektorů
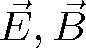 rovinné elektromagnetické vlny
rovinné elektromagnetické vlny
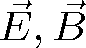 |
(1.37) |
odkud
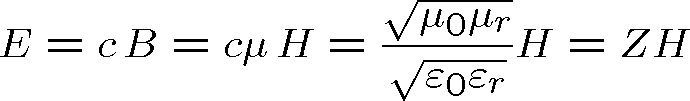 |
(1.38) |
Poslední rovnost definuje impedanci Z. Impedance vakua Z0 je rovna
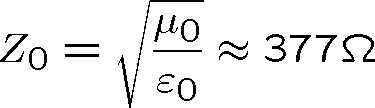 |
(1.39) |
Podle rov. (1.16) je pro nemagnetické prostředí (
 ) impedance rovna
) impedance rovna
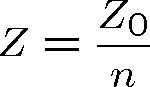 |
(1.40) |
kde n je index lomu látky.
1.3.2 Harmonická rovinná světelná vlna
Jako jedno z nejjednodušších (a pro optiku nejvýznamnějších) řešení vlnové rovnice můžeme uvést rovinnou harmonickou vlnu6,
 |
(1.41) |
Zde
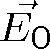 je amplituda vlny,
je amplituda vlny,
 kruhová frekvence. Protože se jedná o vlnění na jedné pevně dané frekvenci, mluví se o monochromatické vlně.
kruhová frekvence. Protože se jedná o vlnění na jedné pevně dané frekvenci, mluví se o monochromatické vlně.
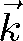 je vlnový vektor definovaný
je vlnový vektor definovaný
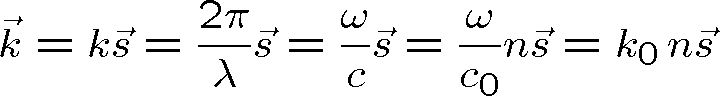 |
(1.42) |
Zde
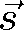 je opět jednotkový vektor ve směru šíření,
je opět jednotkový vektor ve směru šíření,
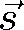 vlnová délka vlny v prostředí,
vlnová délka vlny v prostředí,
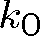 velikost vlnového vektoru ve vakuu. Magnetické pole
velikost vlnového vektoru ve vakuu. Magnetické pole
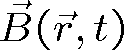 je vyjádřeno analogicky.
je vyjádřeno analogicky.
Pro harmonickou časovou závislost světelné vlny lze provést časovou derivaci a psát vlnovou rovnici v Helmholtzově tvaru7
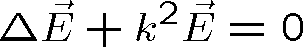 |
(1.43) |
Připomeňme zde všeobecně známý význam parametrů popisujících harmonickou vlnu na příkladu jednodimensionální skalární harmonické vlny postupující ve směru osy z
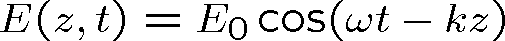 |
(1.44) |
Sledujeme-li výchylku spojenou s vlnou v určitém místě (například
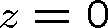 ) opakuje se její maximální hodnota v čase s periodou T, která je důsledkem periodicity funkce cos, a souvisí přímo s kruhovou frekvencí vlny
) opakuje se její maximální hodnota v čase s periodou T, která je důsledkem periodicity funkce cos, a souvisí přímo s kruhovou frekvencí vlny
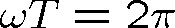 |
(1.45) |
Frekvence vlnění
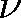 je definována jako počet period za jednotku času8, tedy
je definována jako počet period za jednotku času8, tedy
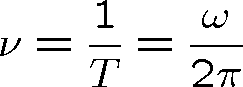 |
(1.46) |
"Zmrazíme-li" vlnu v pevném čase (například
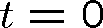 ), opakuje se její maximální hodnota v prostoru s periodou
), opakuje se její maximální hodnota v prostoru s periodou
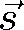 (vlnovou délkou), která je důsledkem periodicity funkce cos, a souvisí s velikostí vlnového vektoru
(vlnovou délkou), která je důsledkem periodicity funkce cos, a souvisí s velikostí vlnového vektoru
 |
(1.47) |
Vzhledem k podstatě vlnění (posun v čase spojen s posunem v prostoru) musí být
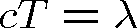 |
(1.48) |
tedy
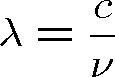 |
(1.49) |
Dále zřejmě platí9
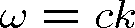 |
(1.50) |
Harmonické rovinné vlny jako speciální případ obecných rovinných vln musí být příčné, jak je uvedeno výše. Lze to ukázat ovšem velmi jednoduše, dosadíme-li elektrické pole ve tvaru rovnice (1.41) do Maxwellových rovnic (pro jednoduchost volíme
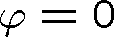 ). Uvážíme přitom, že je
). Uvážíme přitom, že je
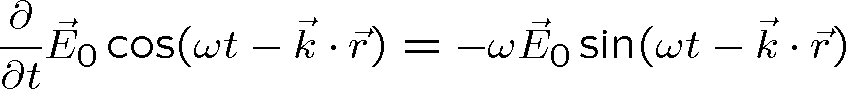 |
(1.51) |
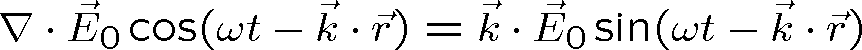 |
(1.52) |
a
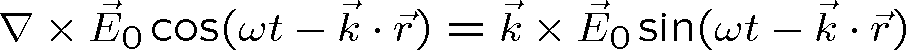 |
(1.53) |
Pak ovšem dostáváme pro vektorové amplitudy vln vztahy odpovídající Maxwellovým rovnicím (1.1 - 1.4)
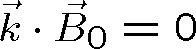 |
(1.54) |
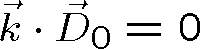 |
(1.55) |
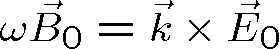 |
(1.56) |
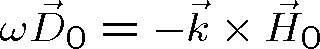 |
(1.57) |
Tyto vztahy ukazují jasně příčnost rovinné (homogenní) harmonické vlny i vzájemnou orientaci vektorů. Harmonická rovinná vlna postupující ve směru osy z je znázorněna na obr. 1.4.
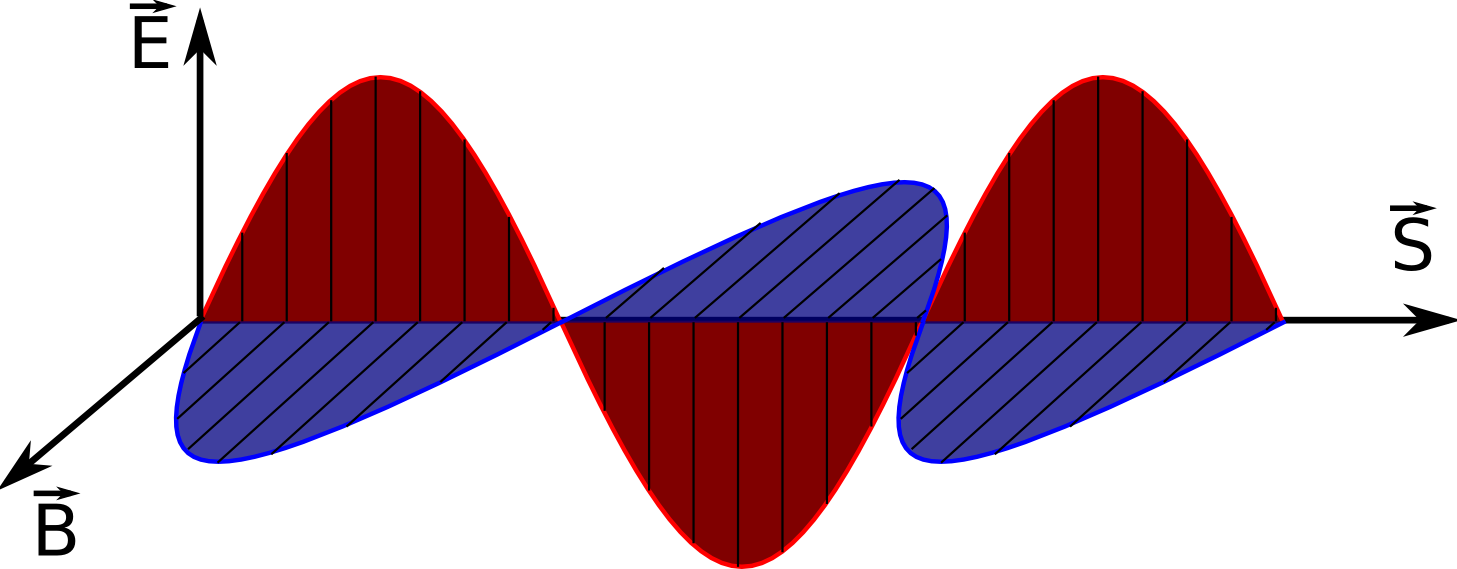 Obr. 1.4
Obr. 1.4 Rovinná elektromagnetická vlna postupující ve směru osy
z
 tvar
tvar
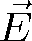
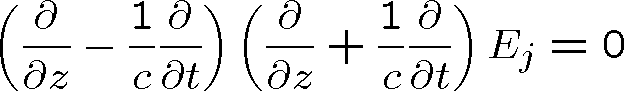
 a
a

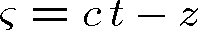
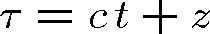
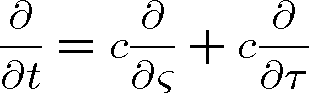
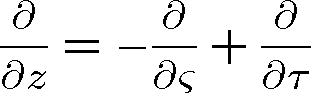
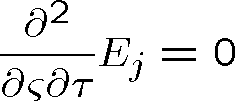

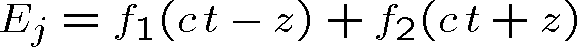
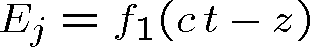
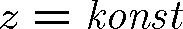 závisí pole jen na čase, v určitém časovém okamžiku závisí pole jen na souřadnici z. Pole bude mít zřejmě stejnou velikost pro všechny souřadnice a časy, které jsou spojeny výrazem
závisí pole jen na čase, v určitém časovém okamžiku závisí pole jen na souřadnici z. Pole bude mít zřejmě stejnou velikost pro všechny souřadnice a časy, které jsou spojeny výrazem
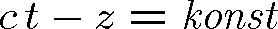
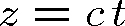 . Geometrické místo stejných hodnot pole, rovina, se tedy bude šířit rychlostí c v kladném směru osy z. Řešení f2 odpovídá rovinné vlně, která běží v záporném smyslu osy z. Pokud chceme vyjádřit rovinnou vlnu v obecném případě, kdy směr náběhu fáze, směr šíření, je určen jednotkovým vektorem
. Geometrické místo stejných hodnot pole, rovina, se tedy bude šířit rychlostí c v kladném směru osy z. Řešení f2 odpovídá rovinné vlně, která běží v záporném smyslu osy z. Pokud chceme vyjádřit rovinnou vlnu v obecném případě, kdy směr náběhu fáze, směr šíření, je určen jednotkovým vektorem
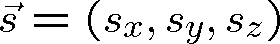 (viz obr. 1.2), bude argument rovinné vlny mít tvar (
(viz obr. 1.2), bude argument rovinné vlny mít tvar (
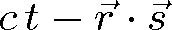 ), protože skalární součin
), protože skalární součin
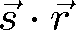 je roven průmětu libovolného polohového vektoru
je roven průmětu libovolného polohového vektoru
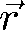 do směru
do směru
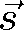 , odpovídá tedy výše uvažované souřadnici z. Tento argument se nazývá fází vlny. Elektrické a magnetické pole rovinné vlny má tedy jednotlivé komponenty, které závisí na fázi vyjádřené v uvedeném tvaru. Aby ovšem vektory elektrického a magnetického pole byly řešením Maxwellových rovnic, musí splňovat ještě další podmínky. Uvažujeme tedy vektory
, odpovídá tedy výše uvažované souřadnici z. Tento argument se nazývá fází vlny. Elektrické a magnetické pole rovinné vlny má tedy jednotlivé komponenty, které závisí na fázi vyjádřené v uvedeném tvaru. Aby ovšem vektory elektrického a magnetického pole byly řešením Maxwellových rovnic, musí splňovat ještě další podmínky. Uvažujeme tedy vektory

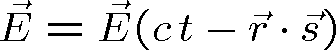
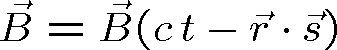
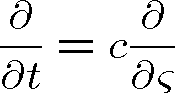
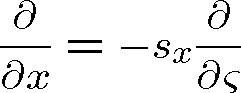 ,
,
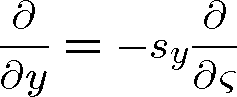 ,
,
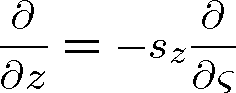 . (1.31)
Proto můžeme vyjádřit
. (1.31)
Proto můžeme vyjádřit
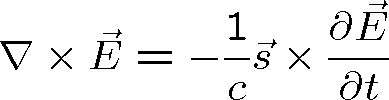
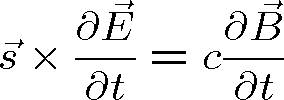
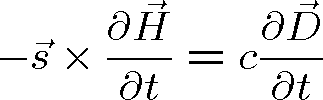
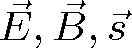
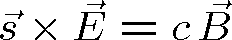
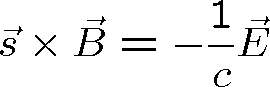
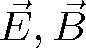 musí být kolmé na směr šíření (skutečně skalární součin
musí být kolmé na směr šíření (skutečně skalární součin
 i kolmé navzájem.5 Pro izotropní prostředí jsou ovšem vektory
i kolmé navzájem.5 Pro izotropní prostředí jsou ovšem vektory
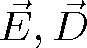 , resp.
, resp.
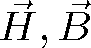 kolineární. Rovinné elektromagnetické vlny jsou tedy v izotropním prostředí příčné, vektory mají vzájemnou orientaci jak je znázorněno na obr. 1.3. Například z rov. (1.35)
kolineární. Rovinné elektromagnetické vlny jsou tedy v izotropním prostředí příčné, vektory mají vzájemnou orientaci jak je znázorněno na obr. 1.3. Například z rov. (1.35)

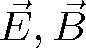 rovinné elektromagnetické vlny
rovinné elektromagnetické vlny
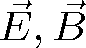
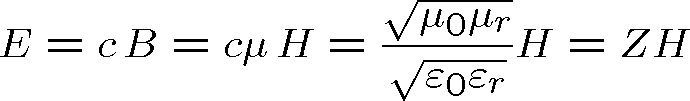
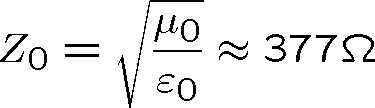
 ) impedance rovna
) impedance rovna
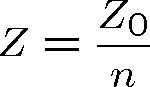

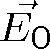 je amplituda vlny,
je amplituda vlny,
 kruhová frekvence. Protože se jedná o vlnění na jedné pevně dané frekvenci, mluví se o monochromatické vlně.
kruhová frekvence. Protože se jedná o vlnění na jedné pevně dané frekvenci, mluví se o monochromatické vlně.
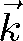 je vlnový vektor definovaný
je vlnový vektor definovaný
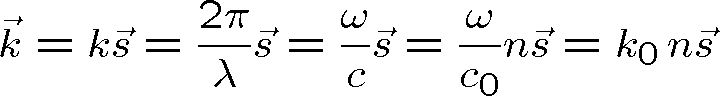
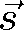 je opět jednotkový vektor ve směru šíření,
je opět jednotkový vektor ve směru šíření,
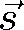 vlnová délka vlny v prostředí,
vlnová délka vlny v prostředí,
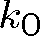 velikost vlnového vektoru ve vakuu. Magnetické pole
velikost vlnového vektoru ve vakuu. Magnetické pole
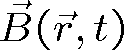 je vyjádřeno analogicky.
je vyjádřeno analogicky.
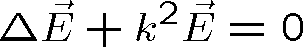
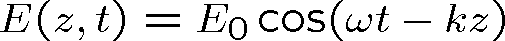
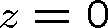 ) opakuje se její maximální hodnota v čase s periodou T, která je důsledkem periodicity funkce cos, a souvisí přímo s kruhovou frekvencí vlny
) opakuje se její maximální hodnota v čase s periodou T, která je důsledkem periodicity funkce cos, a souvisí přímo s kruhovou frekvencí vlny
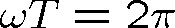
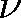 je definována jako počet period za jednotku času8, tedy
je definována jako počet period za jednotku času8, tedy
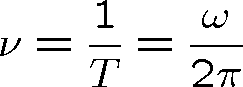
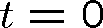 ), opakuje se její maximální hodnota v prostoru s periodou
), opakuje se její maximální hodnota v prostoru s periodou
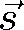 (vlnovou délkou), která je důsledkem periodicity funkce cos, a souvisí s velikostí vlnového vektoru
(vlnovou délkou), která je důsledkem periodicity funkce cos, a souvisí s velikostí vlnového vektoru

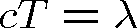
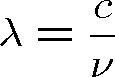
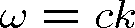
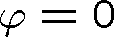 ). Uvážíme přitom, že je
). Uvážíme přitom, že je