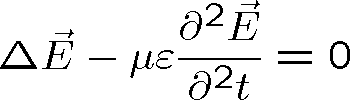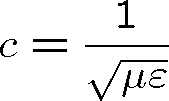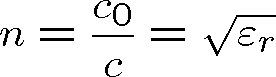1.2 Vlnová rovnice
Šíření světla, které je speciálním případem elektromagnetických vln, popisuje vlnová rovnice, která plyne z Maxwellových rovnic. Připomeňme si nyní, jak z Maxwellových rovnic vlnovou rovnici dostaneme a jaký má tvar pro různá prostředí. V tomto kontextu lze prostředí rozdělit na prostředí homogenní, nehomogenní, izotropní, anizotropní, vodivá a nevodivá. Homogenní prostředí jsou taková, jejichž vlastnosti jsou ve všech místech stejné, nezávisí na prostorové souřadnici. V prostředích nehomogenních naopak na prostorové souřadnici závisí. Izotropní látky mají vlastnosti nezávislé na směru (šíření světla, polarizace apod.), v anizotropních jsou jejich vlastnosti na směru závislé. Rozdělení látek na vodivé a nevodivé je obvyklé v učebnicích o elektřině a magnetismu, kde se mluví zpravidla o dielektrikách a vodičích. Vyjdeme z Maxwellových rovnic
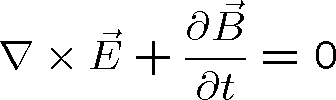 |
(1.1) |
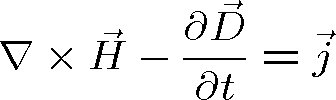 |
(1.2) |
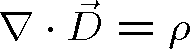 |
(1.3) |
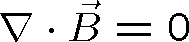 |
(1.4) |
a obvyklých materiálových vztahů
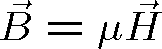 |
(1.5) |
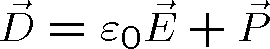 |
(1.6) |
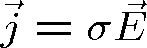 |
(1.7) |
Zde je použité běžné značení veličin:
 je intenzita elektrického pole,
je intenzita elektrického pole,
 je elektrická indukce,
je elektrická indukce,
 je magnetická intenzita,
je magnetická intenzita,
 magnetická indukce,
magnetická indukce,
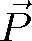 elektrická polarizace,
elektrická polarizace,
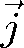 hustota elektrického proudu, ρ hustota elektrického náboje, μ je magnetická permeabilita, ε0 permitivita vakua a σ elektrická vodivost. Budeme se zabývat šířením světla v látkách nemagnetických, tedy
hustota elektrického proudu, ρ hustota elektrického náboje, μ je magnetická permeabilita, ε0 permitivita vakua a σ elektrická vodivost. Budeme se zabývat šířením světla v látkách nemagnetických, tedy
 . Ve většině případů (kromě 16. kapitoly) budeme také předpokládat lineární závislost polarizace na elektrickém poli, tedy
. Ve většině případů (kromě 16. kapitoly) budeme také předpokládat lineární závislost polarizace na elektrickém poli, tedy
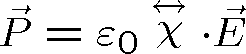 |
(1.8) |
kde
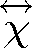 je elektrická susceptibilita (obecně tenzor) a odkud je
je elektrická susceptibilita (obecně tenzor) a odkud je
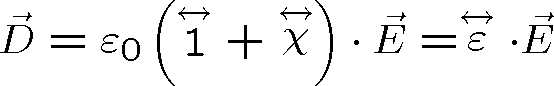 |
(1.9) |
Permitivita
 je obecně tenzorová veličina závislá na prostorových souřadnicích. Výraz v kulatých závorkách v (1.9) definuje relativní permitivitu,
je obecně tenzorová veličina závislá na prostorových souřadnicích. Výraz v kulatých závorkách v (1.9) definuje relativní permitivitu,
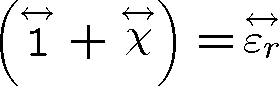 .Vlastnosti permitivity podle typu prostředí jsou shrnuty v tab. 1.2. 1
.Vlastnosti permitivity podle typu prostředí jsou shrnuty v tab. 1.2. 1
|
|
homogenní
|
nehomogenní
|
|
izotropní
|

|


|
|
anizotropní
|
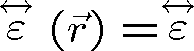
|
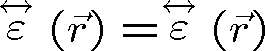
|
Tabulka 1.2 Přehled klasifikace prostředí a odpovídající charakter permitivity
Nyní se budeme zabývat pouze izotropními prostředími, šíření světla anizotropními prostředími budeme podrobně zkoumat v kapitole 13. Aplikujeme-li operátor
 na rovnici (1.1) a uvážíme-li, že můžeme zaměnit pořadí derivací podle času a souřadnice, dostaneme po dosazení z rovnice (1.2)
na rovnici (1.1) a uvážíme-li, že můžeme zaměnit pořadí derivací podle času a souřadnice, dostaneme po dosazení z rovnice (1.2)
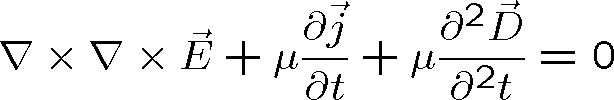 |
(1.10) |
Můžeme nyní použít vektorovou identitu
 |
(1.11) |
Obvykle se dále předpokládá, že
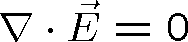 |
(1.12) |
To je splněno například pro homogenní izotropní prostředí bez volného náboje, jak plyne přímo z rovnice (1.3), nebo v dobrých vodičích, kde je amplituda jakéhokoliv náboje v objemu rychle tlumena.2
Platí-li (1.12) a výše uvedené materiálové vztahy, dostáváme vlnovou rovnici ve tvaru (
 je Lapalceův operátor)
je Lapalceův operátor)
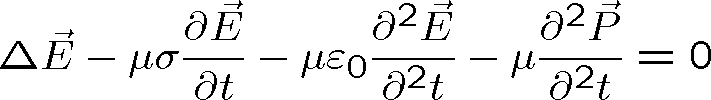 |
(1.13) |
Odtud můžeme získat známé tvary vlnové rovnice. Například pro šíření světla ve vakuu je
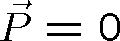 a
a
 . Pro homogenní izotropní dielektrikum (
. Pro homogenní izotropní dielektrikum (
 ), pro které platí (1.8), máme
), pro které platí (1.8), máme
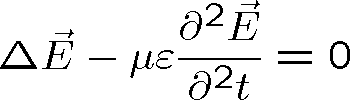 |
(1.14) |
tedy fázová rychlost šíření je
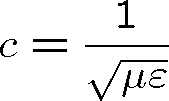 |
(1.15) |
V optice se zavádí veličina index lomu prostředí, jako poměr rychlosti světla ve vakuu k rychlosti světla v daném (nemagnetickém) prostředí,
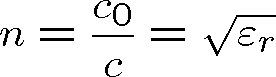 |
(1.16) |
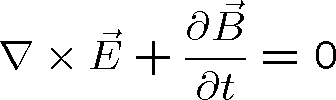
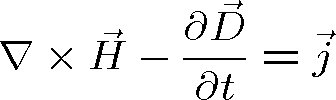
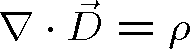
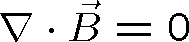
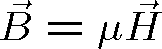
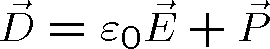
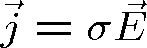
 je intenzita elektrického pole,
je intenzita elektrického pole,
 je elektrická indukce,
je elektrická indukce,
 je magnetická intenzita,
je magnetická intenzita,
 magnetická indukce,
magnetická indukce,
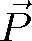 elektrická polarizace,
elektrická polarizace,
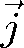 hustota elektrického proudu, ρ hustota elektrického náboje, μ je magnetická permeabilita, ε0 permitivita vakua a σ elektrická vodivost. Budeme se zabývat šířením světla v látkách nemagnetických, tedy
hustota elektrického proudu, ρ hustota elektrického náboje, μ je magnetická permeabilita, ε0 permitivita vakua a σ elektrická vodivost. Budeme se zabývat šířením světla v látkách nemagnetických, tedy
 . Ve většině případů (kromě 16. kapitoly) budeme také předpokládat lineární závislost polarizace na elektrickém poli, tedy
. Ve většině případů (kromě 16. kapitoly) budeme také předpokládat lineární závislost polarizace na elektrickém poli, tedy
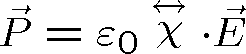
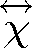 je elektrická susceptibilita (obecně tenzor) a odkud je
je elektrická susceptibilita (obecně tenzor) a odkud je
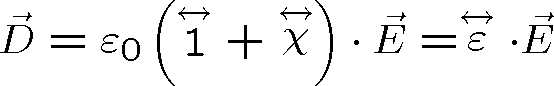
 je obecně tenzorová veličina závislá na prostorových souřadnicích. Výraz v kulatých závorkách v (1.9) definuje relativní permitivitu,
je obecně tenzorová veličina závislá na prostorových souřadnicích. Výraz v kulatých závorkách v (1.9) definuje relativní permitivitu,
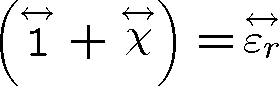 .Vlastnosti permitivity podle typu prostředí jsou shrnuty v tab. 1.2. 1
.Vlastnosti permitivity podle typu prostředí jsou shrnuty v tab. 1.2. 1
 na rovnici (1.1) a uvážíme-li, že můžeme zaměnit pořadí derivací podle času a souřadnice, dostaneme po dosazení z rovnice (1.2)
na rovnici (1.1) a uvážíme-li, že můžeme zaměnit pořadí derivací podle času a souřadnice, dostaneme po dosazení z rovnice (1.2)
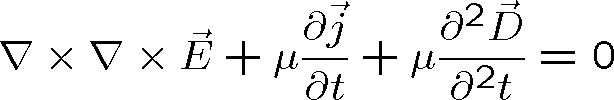

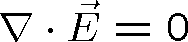
 je Lapalceův operátor)
je Lapalceův operátor)
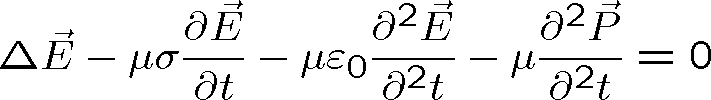
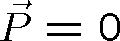 a
a
 . Pro homogenní izotropní dielektrikum (
. Pro homogenní izotropní dielektrikum (
 ), pro které platí (1.8), máme
), pro které platí (1.8), máme