---

---

2.3 Tepelná rovnováha. Teplota

Uvažujme dvě tělesa A a B (soustavy A a B), které uvedeme do vzájemného kontaktu. Ze zkušenosti vyplývá, že mohou nastat dvě možnosti:

1. Mezi tělesy neprobíhá tepelná výměna, tedy Q_A = Q_B = 0. Tělesa se nacházejí ve vzájemné tepelné rovnováze. Tento případ charakterizujeme výrokem, že obě tělesa mají stejnou teplotu.
2. Nastane změna stavu každého tělesa. Mezi tělesy probíhá tepelná výměna a po určité době se vytvoří rovnovážný stav. V tomto případě říkáme, že na počátku děje měla tělesa různou teplotu. Těleso, u něhož během tepelné výměny došlo ke zmenšení jeho vnitřní energie, mělo na počátku děje vyšší teplotu, než těleso druhé.

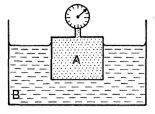Obr. 2-3

Teplota je stavová veličina, která charakterizuje stav termodynamické rovnováhy soustavy. Znalost teploty zkoumaných těles umožňuje říci, zda mezi tělesy nastane tepelná výměna a jaký je její „směr" .

Stav tepelné rovnováhy je tranzitivní; je-li těleso A v tepelné rovnováze s tělesem B a současně těleso B v tepelné rovnováze s tělesem C, jsou také tělesa A a C ve vzájemné tepelné rovnováze. Tato vlastnost tepelné rovnováhy umož-

ňuje vybrat těleso B za zkušební těleso - teploměr. Při výběru teploměru je třeba splnit dva požadavky:

a) Veličina, která popisuje některou vlastnost citlivého elementu teploměru, se musí výrazně monotonně měnit při tepelné výměně. Příkladem je objem kapaliny nebo plynu, tlak, elektrický odpor, termoelektrické napětí, magnetická sus-ceptibilita apod.

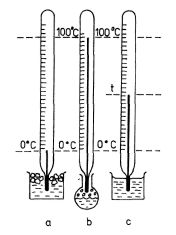Obr. 2-4

b) Citlivý element teploměru nesmí být velkých rozměrů, aby tepelná výměna mezi tělesem a teploměrem neovlivňovala příliš původní teplotu tělesa.

K měření teploty je třeba sestrojit teplotní stupnici a stanovit jednotku teploty. V denní praxi měříme nejčastěji teplotu v Celsiově teplotní stupnici. K jejímu sestrojení volíme dva základní stavy (obr. 2-4):

1. Rovnovážný stav chemický čisté vody a jejího ledu za normálního tlaku . Tomuto stavu přiřazujeme dohodou teplotu 0 °C .
2. Rovnovážný stav chemicky čisté vody a její syté páry za normálního tlaku. Tomuto stavu přiřazujeme dohodou teplotu 100 °C .

Rozdělíme-li teplotní stupnici mezi těmito základními teplotami na 100 stejných dílků, odpovídá jeden dílek teplotnímu rozdílu jednoho Celsiova stupně (1 °C).

Pro běžné účely se zavádí např. empirická rtuťová teplotní stupnice založená na teplotní objemové roztažnosti rtuti (rtuť je výhodná z hlediska tepelné vodivosti). Označíme-li V₀ a V₁₀₀ objem rtuti v baňce teploměru při teplotách 0°C

a 100 °C (viz obr. 2-4a,b), pak 1 °C přísluší změna objemu 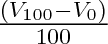. Teplota

t odpovídající objemu V (obr. 2-4c) je pak určena rovnicí

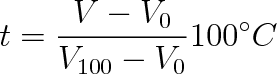(2.6)

resp.

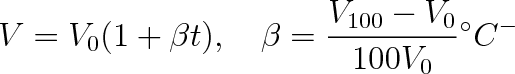kde 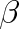je součinitel teplotní objemové roztažnosti.

Důsledkem této definice Celsiovy teploty t je lineární objemová roztažnost rtuti s teplotou.

Jestliže za teplotoměrnou látku zvolíme jinou kapalinu a postupujeme obdobně, pak se podle vztahu (2.6) tato kapalina roztahuje „ve své stupnici" s teplotou lineárně, ale závislost V(t) u ostatních kapalin (např. rtuti) je vzhledem k této teplotě obecně nelineární. Nesouhlas je dán tím, že součinitelé teplotní objemové roztažnosti 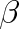kapalin jsou obecně závislé na teplotě.

Situace se zlepší, použijeme-li za náplň teploměru plyny jako vodík, kyslík, dusík, oxid uhličitý a vzácné plyny . Z experimentů s těmito plyny za sníženého tlaku vyplynul závěr (Gay--Lussac, Charles, Boyle, Mariotte), že se jejich objem vzhledem k rtuťové teplot-

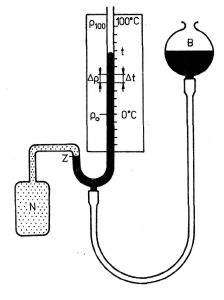Obr. 2-5

ní stupnici mění s teplotou přibližně stejně, třeba ne zcela rovnoměrně. Této skutečnosti bylo využito k definici tzv. plynové teplotní stupnice.

Protože je snažší měřit proměnný tlak plynu při konstantním objemu než obráceně, realizuje se plynová teplotní stupnice pomocí rozpínavosti (změny tlaku s teplotou) plynu.

Označme p₀ a p₁₀₀ tlak plynu v nádobce N plynového teploměru, při teplotách 0 C a 100 °C. Potom teplota t odpovídající tlaku p je určena rovnicí

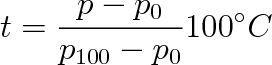(2.7)

Odtud plyne

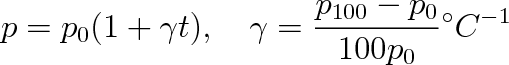kde 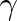je součinitel teplotní rozpínavosti plynu. Měřením pro dostatečně zředěné plyny vychází součinitel 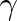přibližně stejný pro všechny plyny a má hodnotu 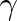= 3,661 . 10^-3 °C^-1.

Označíme-li t₀ = 1/ 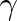, je t₀ = 273,15 °C. Vztah pro závislost tlaku plynu na teplotě t můžeme pak psát ve tvaru

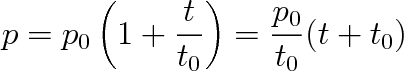(2.8)

Ze vztahu (2.8) vyplývá, že při Celsiově teplotě t = -273,15 °C by tlak plynu byl nulový. Protože tlak plynu nemůže být záporný, nemůže plyn existovat při teplotě -273,15 °C a nižší teplotě. Byla proto zavedena teplotní plynová stupnice, ve které odečítáme teplotu od této minimální hodnoty, ale označujeme jí jako nulový (počáteční bod) - tzv. absolutní nula. Takto vytvořená stupnice pouze s nezápornými hodnotami a jejíž 1 stupeň je stejně veliký jako 1 °C dostala název absolutní teplotní stupnice nebo také Kelvinova teplotní stupnice. Teplota v ní měřená se nazývá absolutní teplota T . a udává se v kelvinech (K). S Celsiovou teplotou t souvisí vztahem

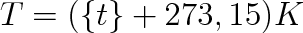(2.9)

kde {t} je číselná hodnota Celsiovy teploty t.

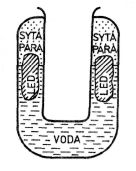
Za základní definiční bod absolutní teplotní stupnice byl zvolen (nepočítáme--li výchozí nulový bod) trojný bod vody. Je to rovnovážný stav soustavy led + voda + sytá vodní pára. Teplota této soustavy byla definitoricky stanovena hodnotou T_r = 273,16 K. Trojný bod vody lze velmi přesně a poměrně snadno

Obr. 2-6

realizovat v zařízení, jehož zjednodušené schéma je na obr. 2-6. Do dutiny se pak při sestrojování teplotní stupnice ukládá baňka plynového teploměru.

Jednotka kelvin (K) je definována jako 273,16-tá část teploty trojného bodu vody.

Zavedením absolutní teploty T a označením T₀ = 273,15 K zapíšeme vztah (2.8) ve tvaru

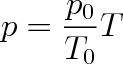(2.10)

Vztahem (2.10) je tedy definována absolutní teplota T úměrná tlaku p plynu při konstantním objemu (izochorický zákon - zákon Charlesův). Podobně lze psát pro změnu objemu V s absolutní teplotou T při konstantním tlaku plynu vztah

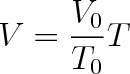(2.11)

(izobarický zákon - zákon Gay-Lussacův).

---

---