Vypočteme, jak rychle se valí po nakloněné rovině homogenní rotačně symetrické těleso znázorněné v průmětu na rovinu kolmou k ose symetrie tělesa na obr.89. Předpokládáme, že valení probíhá tak, že osa rotační symetrie tělesa je rovnoběžná s průsečnicí nakloněné roviny s vodorovnou rovinou.
Valením rozumíme takový vzájemný
pohyb dvou těles, při kterém jejich dotyková přímka (průmět je na obrázku
označen o
) je okamžitou osou otáčení (srov. stať 6.5.2). V případě
znázorněném na obr.89 to znamená, že (statický) součinitel tření
(4,55)
mezi
rovinou a tělesem je natolik velký, aby bylo možno realizovat sílu tření
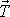 nezbytnou k roztočení tělesa. Když
podmínka velikosti součinitele statického tření pro daný náklon není splněna,
těleso se po nakloněné rovině nevalí, ale smýká. Dotyková přímka není okamžitou
pevnou přímkou v tělese, a není tedy okamžitou osou otáčení.
nezbytnou k roztočení tělesa. Když
podmínka velikosti součinitele statického tření pro daný náklon není splněna,
těleso se po nakloněné rovině nevalí, ale smýká. Dotyková přímka není okamžitou
pevnou přímkou v tělese, a není tedy okamžitou osou otáčení.
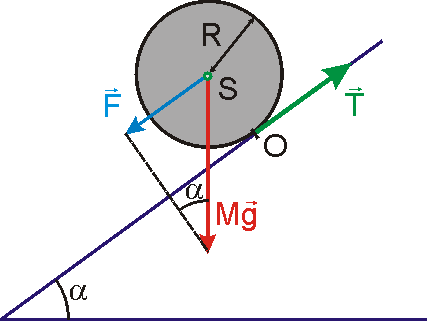 Hmotný střed S tělesa, který leží na ose
rotační symetrie, se v případě znázorněném na obr.89 pohybuje podél
nakloněné roviny ve vzdálenosti R
od ní. Vnější síly působící na těleso jsou jeho tíha
Hmotný střed S tělesa, který leží na ose
rotační symetrie, se v případě znázorněném na obr.89 pohybuje podél
nakloněné roviny ve vzdálenosti R
od ní. Vnější síly působící na těleso jsou jeho tíha
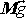 , reakce pod-ložky udržující těleso na nakloněné rovině (vazbová síla) a síla tření
, reakce pod-ložky udržující těleso na nakloněné rovině (vazbová síla) a síla tření
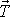 . Reakce podložky má směr kolmý k možnému směru pohybu hmotného středu
tělesa, a proto pohyb neovlivňuje. Má-li se těleso po nakloněné rovině valit,
musí mezi tělesem a nakloněnou rovinou působit síla smyko-vého tření
. Reakce podložky má směr kolmý k možnému směru pohybu hmotného středu
tělesa, a proto pohyb neovlivňuje. Má-li se těleso po nakloněné rovině valit,
musí mezi tělesem a nakloněnou rovinou působit síla smyko-vého tření
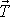 . Kdyby síla tření
. Kdyby síla tření
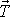 byla nulová nebo nedostatečně velká, těleso
by se po nakloněné rovině nevalilo, ale klouzalo by po ní, jak jsme již uvedli.
byla nulová nebo nedostatečně velká, těleso
by se po nakloněné rovině nevalilo, ale klouzalo by po ní, jak jsme již uvedli.
Dle věty
(5,35)
výsledná vnější síla
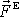 působící na těleso je rovna hmotnosti M
tělesa násobené zrychlením
působící na těleso je rovna hmotnosti M
tělesa násobené zrychlením
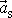 jeho hmotného středu;
jeho hmotného středu;
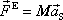 . . |
(5,35) |
Budeme uvažovat složku této rovnice do směru možného pohybu
hmotného středu S tělesa valícího se po nakloněné rovině. Složka tíhy
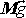 do uvažovaného směru, na obr.89
označená
do uvažovaného směru, na obr.89
označená
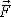 , má velikost
, má velikost
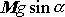 . Síla tření
. Síla tření
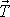 leží přímo v uvažovaném směru a má
opačný smysl než síla
leží přímo v uvažovaném směru a má
opačný smysl než síla
 . Pokládáme-li zrychlení ve smyslu
. Pokládáme-li zrychlení ve smyslu
 za kladné, můžeme složku rovnice
(5,35)
do
směru pohybu hmotného středu S zapsat
v tvaru
za kladné, můžeme složku rovnice
(5,35)
do
směru pohybu hmotného středu S zapsat
v tvaru
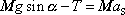 . . |
(7,37) |
V rovnici
(7,37)
neznáme hodnoty
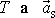 . Druhou rovnici pro stanovení těchto hodnot získáme aplikací rovnice pro otáčení
tuhého tělesa kolem pevné osy
(6,12)
na uvažovaný příklad. Za osu otáčení
tělesa pokládáme osu procházející jeho hmotným středem, tedy osu rotační
symetrie tělesa. Moment setrvačnosti tělesa vůči této ose označíme J.
Moment
. Druhou rovnici pro stanovení těchto hodnot získáme aplikací rovnice pro otáčení
tuhého tělesa kolem pevné osy
(6,12)
na uvažovaný příklad. Za osu otáčení
tělesa pokládáme osu procházející jeho hmotným středem, tedy osu rotační
symetrie tělesa. Moment setrvačnosti tělesa vůči této ose označíme J.
Moment
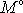 vnějších sil vůči ose vytváří pouze síla tření
vnějších sil vůči ose vytváří pouze síla tření
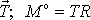 , kde R je vzdálenost hmotného středu S od nakloněné
roviny. Pro válec nebo kouli je R
jejich poloměr. Dosazením do rovnice
(6,12)
dostáváme
, kde R je vzdálenost hmotného středu S od nakloněné
roviny. Pro válec nebo kouli je R
jejich poloměr. Dosazením do rovnice
(6,12)
dostáváme
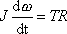 . . |
(7,38) |
Z geometrie řešeného příkladu plyne, že rychlost hmotného středu
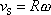 . . |
(7,39) |
Derivováním rovnice
(7,39)
dle času t
získáme vztah mezi postupným zrychlením hmotného středu
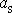 a úhlovým zrychlením
a úhlovým zrychlením
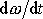 ;
;
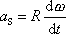 . . |
Dosadíme-li
 za
za
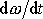 do
(7,38)
, dostáváme po úpravě
do
(7,38)
, dostáváme po úpravě
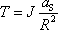 . . |
(7,40) |
Dle (7,40) dosadíme za T do rovnice (7,37) , dostaneme
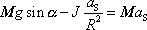 , , |
odkud
Hodnota zrychlení
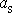 je konstantní. Hmotný střed tělesa, které se
valí po nakloněné rovině, koná rovnoměrně zrychlený pohyb. Dosadíme-li do
(7,40)
hodnotu
je konstantní. Hmotný střed tělesa, které se
valí po nakloněné rovině, koná rovnoměrně zrychlený pohyb. Dosadíme-li do
(7,40)
hodnotu
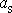 danou rovnicí
(7,41)
, zjistíme velikost
smykového tření
danou rovnicí
(7,41)
, zjistíme velikost
smykového tření
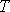 nezbytnou k tomu, aby se těleso po
nakloněné rovině nesmýkalo, ale valilo.
nezbytnou k tomu, aby se těleso po
nakloněné rovině nesmýkalo, ale valilo.
Pro
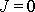 plyne z
(7,41)
, že
plyne z
(7,41)
, že
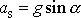 . Výraz
. Výraz
 je známé [1] zrychlení tělesa, které
se po nakloněné rovině smýká bez tření označíme je
je známé [1] zrychlení tělesa, které
se po nakloněné rovině smýká bez tření označíme je
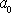 . Všechny veličiny vystupující v rovnici
(7,41)
jsou kladné, a tedy pro
. Všechny veličiny vystupující v rovnici
(7,41)
jsou kladné, a tedy pro
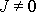 je
je
 menší než
menší než
 .
.
Zrychlení
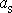 tělesa, které se po nakloněné rovině valí, je menší než zrychlení
tělesa, které se po nakloněné rovině valí, je menší než zrychlení
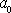 tělesa, které se po nakloněné rovině smýká bez tření.
tělesa, které se po nakloněné rovině smýká bez tření.
Výpočtem dle rovnice
(6,9)
lze
zjistit, že moment setrvačnosti homogenního válce vůči jeho rotační ose je
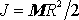 , kde M je hmotnost a R
poloměr válce. Dosadíme-li uvedený moment setrvačnosti do rovnice
(7,41)
, dostaneme
, kde M je hmotnost a R
poloměr válce. Dosadíme-li uvedený moment setrvačnosti do rovnice
(7,41)
, dostaneme
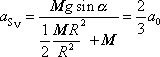 . . |
(7,42) |
Zrychlení
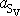 hmotného středu homogenního válce, který se
valí po nakloněné rovině, je rovno dvěma třetinám zrychlení tělesa, které se po
nakloněné rovině smýká bez tření. Moment setrvačnosti koule vůči ose
procházející jejím hmotným středem je
hmotného středu homogenního válce, který se
valí po nakloněné rovině, je rovno dvěma třetinám zrychlení tělesa, které se po
nakloněné rovině smýká bez tření. Moment setrvačnosti koule vůči ose
procházející jejím hmotným středem je
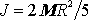 . Dosadíme-li tuto hodnotu do
(7,41)
, dostáváme pro zrychlení
. Dosadíme-li tuto hodnotu do
(7,41)
, dostáváme pro zrychlení
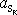 hmotného středu koule vyjádření
hmotného středu koule vyjádření
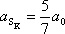 . . |
(7,43) |
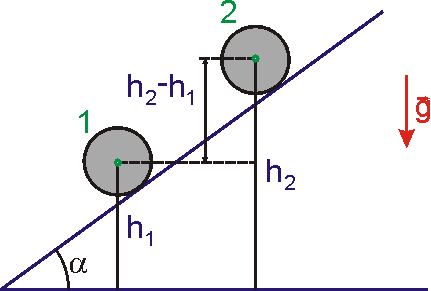 Porovnáním rovnic
(7,42)
a
(7,43)
zjistíme, že
Porovnáním rovnic
(7,42)
a
(7,43)
zjistíme, že
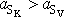 . Vypustíme-li z jednoho místa nakloněné roviny současně válec a kouli,
které pů-vodně byly v klidu, koule válec předběhne. Tento závěr platí bez
ohledu na velikost koule nebo válce, ovšem jen potud, pokud pohyb není
podstatně ovlivněn vnějšími vlivy, např. působením valivého tření
(4,56)
.
. Vypustíme-li z jednoho místa nakloněné roviny současně válec a kouli,
které pů-vodně byly v klidu, koule válec předběhne. Tento závěr platí bez
ohledu na velikost koule nebo válce, ovšem jen potud, pokud pohyb není
podstatně ovlivněn vnějšími vlivy, např. působením valivého tření
(4,56)
.
Síla tření
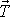 vytváří nezbytnou podmínku pro vznik valení,
ale nedisipuje žádnou energii. Proto na valení po nakloněné rovině můžeme
aplikovat zákon zachování energie. Na obr.90 jsou znázorněny dvě polohy tělesa
na nakloněné rovině. Označíme-li
vytváří nezbytnou podmínku pro vznik valení,
ale nedisipuje žádnou energii. Proto na valení po nakloněné rovině můžeme
aplikovat zákon zachování energie. Na obr.90 jsou znázorněny dvě polohy tělesa
na nakloněné rovině. Označíme-li
 a
a
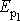 kinetickou a potenciální energii tělesa
v místě 1,
kinetickou a potenciální energii tělesa
v místě 1,
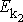 a
a
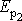 kinetickou a potenciální energii
v místě 2, musí dle zákona zachování mechanické energie
(5,67)
platit
kinetickou a potenciální energii
v místě 2, musí dle zákona zachování mechanické energie
(5,67)
platit
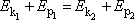 . . |
(7,44) |
Potenciální energii tělesa v tíhovém poli lze (viz čl.
5.7) vyjádřit jako potenciální energii hmotného bodu o hmotnosti M
celého tělesa, který je umístěn v hmotném středu tělesa. Tedy potenciální energie
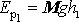 a potenciální energie
a potenciální energie
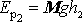 , kde
, kde
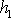 a
a
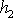 jsou výšky v tíhovém poli, jak plyne
z obr.90. Kinetickou energii
jsou výšky v tíhovém poli, jak plyne
z obr.90. Kinetickou energii
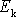 vyjádříme dle Königovy věty (rovnice
(5,74)
)
jako součet
vyjádříme dle Königovy věty (rovnice
(5,74)
)
jako součet
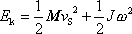 |
(7,45) |
kinetické energie
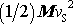 příslušné pohybu hmotného středu tělesa a
vnitřní kinetické energie, která dle
(6,68)
pro těleso rotující kolem osy
je
příslušné pohybu hmotného středu tělesa a
vnitřní kinetické energie, která dle
(6,68)
pro těleso rotující kolem osy
je
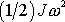 . Budeme-li předpokládat, že v místě 1 je těleso v klidu, potom
. Budeme-li předpokládat, že v místě 1 je těleso v klidu, potom
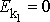 . Označíme-li v místě 2 postupnou rychlost hmotného středu
. Označíme-li v místě 2 postupnou rychlost hmotného středu
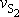 a úhlovou rychlost
a úhlovou rychlost
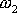 , je
, je
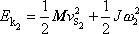 . . |
Se získanými výrazy pro
 má rovnice
(7,44)
tvar
má rovnice
(7,44)
tvar
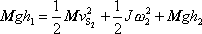 . . |
(7,46) |
Dosadíme-li za
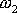 dle
(7,39)
, můžeme z rovnice
(7,46)
vypočítat rychlost
dle
(7,39)
, můžeme z rovnice
(7,46)
vypočítat rychlost
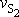 ;
;
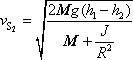 . . |
(7,47) |
Porovnáme-li rychlost
(7,47)
s rychlostí
(4,23)
,
zjistíme, že valící se těleso při pohybu po nakloněné rovině získá mezi místy
se stejnou výškovou odlehlostí
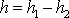 menší rychlost než hmotný bod, a tedy též
než těleso smýkající se po nakloněné rovině bez tření. Výraz
(7,47)
by byl
roven výrazu
(4,23)
pouze pro
menší rychlost než hmotný bod, a tedy též
než těleso smýkající se po nakloněné rovině bez tření. Výraz
(7,47)
by byl
roven výrazu
(4,23)
pouze pro
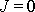 .
.
Budeme nyní předpokládat, že místo 2 vyznačené na obr.90 se
pohybuje současně s tělesem. Provedeme-li derivaci
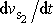 a uvědomíme-li si, že na pravé rovnice
(7,47)
jedinou proměnnou veličinou je
a uvědomíme-li si, že na pravé rovnice
(7,47)
jedinou proměnnou veličinou je
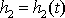 , dostáváme
, dostáváme
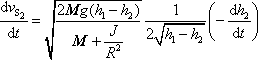 . . |
Z geometrie příkladu (viz obr.90) zřejmě plyne
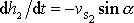 , a tedy
, a tedy
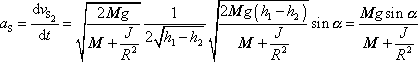 . . |
Poslední výraz je shodný s vyjádřením
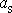 dle rovnice
(7,41)
. Ukázali jsme, že oba
postupy užité v tomto článku pro vyšetřování pohybu tělesa valícího se po
nakloněné rovině dávají stejný výraz pro zrychlení
dle rovnice
(7,41)
. Ukázali jsme, že oba
postupy užité v tomto článku pro vyšetřování pohybu tělesa valícího se po
nakloněné rovině dávají stejný výraz pro zrychlení
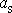 hmotného středu tělesa.
hmotného středu tělesa.