Mějme těleso, které se v tíhovém poli otáčí kolem pevné vodorovné osy neprocházející jeho hmotným středem. Takovému tělesu říkáme fyzické kyvadlo. Jako pro těleso otáčející se kolem pevné osy platí pro jeho pohyb rovnice (6,12)
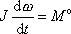 . . |
(6,12) |
 Moment vnějších sil vůči ose
Moment vnějších sil vůči ose
 vytváří tíhové pole, moment
setrvačnosti J je momentem setrvačnosti
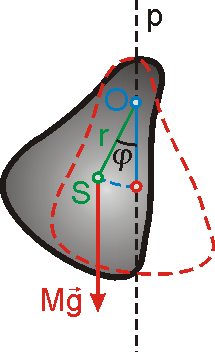
kyvadla vůči ose otáčení. Na obr.86 je schematicky znázorněn pohled na fyzické
kyvadlo ve směru osy otáčení O. Hmotný střed kyvadla je označen S a jeho
vzdálenost od osy otáčení r. Svislá přímka vedená osou otáčení je
značena p
. Dle výsledku uvedeného na konci čl.5.7 lze silové působení na
těleso v tíhovém poli nahradit tíhou tělesa
vytváří tíhové pole, moment
setrvačnosti J je momentem setrvačnosti
kyvadla vůči ose otáčení. Na obr.86 je schematicky znázorněn pohled na fyzické
kyvadlo ve směru osy otáčení O. Hmotný střed kyvadla je označen S a jeho
vzdálenost od osy otáčení r. Svislá přímka vedená osou otáčení je
značena p
. Dle výsledku uvedeného na konci čl.5.7 lze silové působení na
těleso v tíhovém poli nahradit tíhou tělesa
 umístěnou v hmotném středu (těžišti)
tělesa, a tedy velikost momentu síly vůči ose
umístěnou v hmotném středu (těžišti)
tělesa, a tedy velikost momentu síly vůči ose
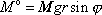 . . |
(7,24) |
V rovnici
(7,24)
jsme označili
 úhel mezi svislou přímkou p
a kolmicí spuštěnou z hmotného středu S
tělesa na osu otáčení O. Úhel
úhel mezi svislou přímkou p
a kolmicí spuštěnou z hmotného středu S
tělesa na osu otáčení O. Úhel
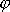 je tedy úhlem mezi přímkou pevnou
v prostoru a přímkou pevnou v tělese, jakým se zpravidla popisuje
pohyb tělesa otáčejícího se kolem pevné osy. Úhlová rychlost otáčení kyvadla
je
je tedy úhlem mezi přímkou pevnou
v prostoru a přímkou pevnou v tělese, jakým se zpravidla popisuje
pohyb tělesa otáčejícího se kolem pevné osy. Úhlová rychlost otáčení kyvadla
je
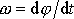 . Dosadíme-li do rovnice
(6,12)
. Dosadíme-li do rovnice
(6,12)
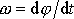 za
za
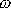 a za
a za
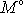 výraz
(7,24)
, dostáváme
výraz
(7,24)
, dostáváme
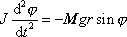 . . |
(7,25) |
Znaménko minus v rovnici
(7,25)
vyjadřuje skutečnost,
že moment tíhové síly se snaží tělesem otáčet v opačném smyslu, než je
smysl úhlu
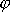 (předpokládáme
(předpokládáme
 ). Rovnice
(7,25)
je diferenciální rovnice
pro neznámou funkci
). Rovnice
(7,25)
je diferenciální rovnice
pro neznámou funkci
 . Funkce
. Funkce
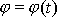 řešící rovnici
(7,25)
není žádná
z běžných funkcí. Její hodnoty mohou být udány tabulkou nebo je možno
funkci vyjádřit ve tvaru nekonečné řady (např. [5]). Omezíme-li se na malé
velikosti úhlu
řešící rovnici
(7,25)
není žádná
z běžných funkcí. Její hodnoty mohou být udány tabulkou nebo je možno
funkci vyjádřit ve tvaru nekonečné řady (např. [5]). Omezíme-li se na malé
velikosti úhlu
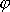 , můžeme použít přibližné rovnosti
, můžeme použít přibližné rovnosti
 a rovnici
(7,25)
přepsat na tvar
a rovnici
(7,25)
přepsat na tvar
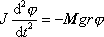 . . |
(7,26) |
Rovnice (7,26) je rovnice formálně shodná s pohybovou rovnicí (2,10) harmonického kmitu. Řešením rovnice (7,26) je tedy funkce
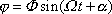 , , |
(7,27) |
kde
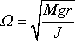 . . |
(7,28) |
Konstanty
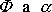 z rovnice
(7,27)
je nutno určit
z počátečních podmínek pohybu. Úhel
z rovnice
(7,27)
je nutno určit
z počátečních podmínek pohybu. Úhel
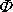 určuje maximální velikost (amplitudu)
úhlu
určuje maximální velikost (amplitudu)
úhlu
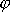 a úhel
a úhel
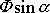 hodnotu úhlu
hodnotu úhlu
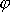 v čase
v čase
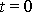 . Je-li
. Je-li
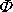 malé, jsou po celou dobu pohybu, tj. pro
všechna
malé, jsou po celou dobu pohybu, tj. pro
všechna
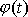 splněny podmínky pro platnost přibližné
rovnice
splněny podmínky pro platnost přibližné
rovnice
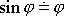 užité při odvození pohybové rovnice
(7,26)
.
Rovnovážná poloha fyzického kyvadla nastane zřejmě (viz též čl.5.8) pro
užité při odvození pohybové rovnice
(7,26)
.
Rovnovážná poloha fyzického kyvadla nastane zřejmě (viz též čl.5.8) pro
 .
.
Při malých výchylkách z rovnovážné polohy je úhel
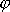 určující pohyb fyzického kyvadla dán
harmonickou rovnicí
(7,27)
. Kyvadlo kmitá kolem své rovnovážné polohy frekvencí
určující pohyb fyzického kyvadla dán
harmonickou rovnicí
(7,27)
. Kyvadlo kmitá kolem své rovnovážné polohy frekvencí
 danou rovnicí
(7,28)
. Je třeba dobře
rozlišovat konstantní frekvenci kmitů
danou rovnicí
(7,28)
. Je třeba dobře
rozlišovat konstantní frekvenci kmitů
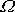 a proměnou úhlovou rychlost
a proměnou úhlovou rychlost
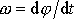 , jakou se kyvadlo otáčí kolem osy. Stejně tak je si třeba uvědomit, že primární
harmonicky proměnou veličinou při pohybu kyvadla je úhel
, jakou se kyvadlo otáčí kolem osy. Stejně tak je si třeba uvědomit, že primární
harmonicky proměnou veličinou při pohybu kyvadla je úhel
 a ne nějaká veličina s délkovým
fyzikálním rozměrem. Takovou veličinou může být průmět polohy hmotného středu S
do vodorovné roviny. Pro tento průmět, kterým se často při elementárním výkladu [1]
pohyb kyvadla vyjadřuje, přibližně také pro malé výchylky platí harmonická
závislost na čase, ale jedná se o zprostředkovanou (sekundární) závislost.
a ne nějaká veličina s délkovým
fyzikálním rozměrem. Takovou veličinou může být průmět polohy hmotného středu S
do vodorovné roviny. Pro tento průmět, kterým se často při elementárním výkladu [1]
pohyb kyvadla vyjadřuje, přibližně také pro malé výchylky platí harmonická
závislost na čase, ale jedná se o zprostředkovanou (sekundární) závislost.
Dobou kmitu T nazýváme časový interval, po kterém se celý pohyb kyvadla opakuje. Dle rovnic (7,27) a (7,28) zřejmě
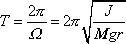 . . |
(7,30) |
Doba kmitu fyzického kyvadla je přímo úměrná odmocnině z momentu setrvačnosti J kyvadla vůči ose otáčení a nepřímo úměrná odmocnině ze součinu hmotnosti M kyvadla, velikosti tíhového zrychlení g a vzdálenosti r hmotného středu kyvadla od osy otáčení.
Porovná-li se řešení
(7,27)
rovnice
(7,26)
s řešením
přesné rovnice
(7,25)
, lze zjistit, že doba kmitu kyvadla je dána výrazem
(7,30)
s přesností lepší než 0,1%,
když amplituda
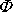 úhlu
úhlu
 nepřesáhne hodnotu 5o.
Výraz
(7,30)
je s touto přesností na amplitudě
nepřesáhne hodnotu 5o.
Výraz
(7,30)
je s touto přesností na amplitudě
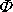 nezávislý. Doba kmitu odpovídající řešení
přesné rovnice
(7,25)
na amplitudě
nezávislý. Doba kmitu odpovídající řešení
přesné rovnice
(7,25)
na amplitudě
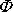 závisí, její hodnotu lze udat ve tvaru
nekonečné řady [3], [14]
s prvním členem rovným výrazu
(7,30)
.
závisí, její hodnotu lze udat ve tvaru
nekonečné řady [3], [14]
s prvním členem rovným výrazu
(7,30)
.
 Předpokládáme-li, že těleso má celou svou
hmotnost M
soustředěnou v bodě, jehož vzdálenost od osy otáčení je
Předpokládáme-li, že těleso má celou svou
hmotnost M
soustředěnou v bodě, jehož vzdálenost od osy otáčení je
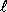 , moment setrvačnosti tělesa vůči ose otáčení je
, moment setrvačnosti tělesa vůči ose otáčení je
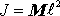 a vzdálenost hmotného středu tělesa od osy otáčení
a vzdálenost hmotného středu tělesa od osy otáčení
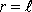 . Pro dobu kmitu takového tělesa, které nazýváme matematickým kyvadlem,
dostáváme dosazením do vzorce
(7,30)
vyjádření
. Pro dobu kmitu takového tělesa, které nazýváme matematickým kyvadlem,
dostáváme dosazením do vzorce
(7,30)
vyjádření
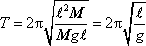 . . |
(7,31) |
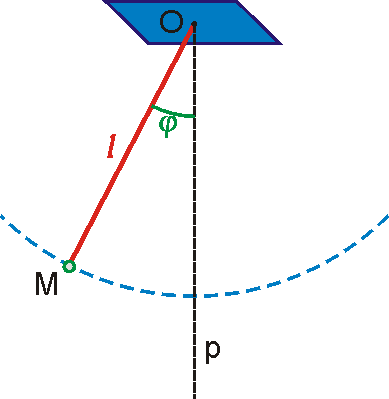
Matematické kyvadlo přibližně realizujeme, zavěsíme-li v tíhovém poli těžkou kouli na lehké vlákno, a počáteční podmínky pohybu volíme tak, aby koule a její závěs se stále pohybovaly v jedné svislé rovině (viz obr.87). Koule (hmotný bod) na lehkém (nehmotném) závěsu může však konat i celou řadu pohybů, které nelze popsat funkcí (7,27) a dobou kmitu (7,31) . Nemusí např. zachovávat rovinu kyvu, což při aplikaci rovnice (7,27) na pohyb matematického kyvadla předpokládáme. Složitější pohyby matematického kyvadla jsou rozebrány např. v [14].
Výraz
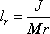 |
(7,32) |
z rovnice (7,30) má rozměr délky a bývá nazýván redukovanou délkou fyzického kyvadla. Užijeme-li v rovnici (7,30) označení (7,32) , dostáváme pro dobu kmitu fyzického kyvadla výraz
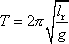 , , |
který je formálně shodný
s rovnicí
(7,31)
. Fyzické kyvadlo s redukovanou délkou
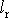 má tedy dobu kmitu stejnou jako matematické
kyvadlo délky
má tedy dobu kmitu stejnou jako matematické
kyvadlo délky
 .
.
Zjistíme, kolem kterých os mají malé kmity fyzického kyvadla
stejnou dobu kmitu. Na obr.88 je naznačen hmotný střed S tělesa, průměty dvou
rovnoběžných os 0 a 0´ a vzdálenosti r´ a r
os od hmotného středu. Doba kmitu T
pro osu 0 je dána výrazem
(7,30)
, dobu kmitu
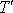 pro osu 0´ zapíšeme ve tvaru
pro osu 0´ zapíšeme ve tvaru
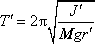 , , |
kde J´
je moment setrvačnosti tělesa vůči ose 0´. Mají-li být doby kmitu T
a
 stejné, musí platit relace
stejné, musí platit relace
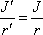 . . |
(7,33) |
Dle Steinerovy věty
(6,61)
můžeme psát
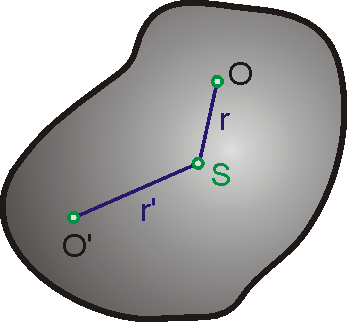
 |
, když moment setrvačnosti vůči ose procházející hmotným
středem S tělesa rovnoběžně s osami O a O´ označíme
 . Zavedeme-li toto vyjádření
. Zavedeme-li toto vyjádření
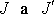 do rovnice
(7,33)
, dostáváme
do rovnice
(7,33)
, dostáváme
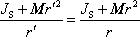 . . |
(7,34) |
Po algebraických úpravách můžeme rovnici
(7,34)
napsat jako
kvadratickou rovnici pro neznámou délku
 ;
;
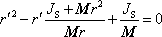 . . |
(7,35) |
Jedním řešením rovnice
(7,35)
je
 , jak lze přímo zjistit z rovnice
(7,33)
a
(7,34)
. Fyzické kyvadlo kývá se
stejnou dobou kmitu kolem všech rovnoběžných os stejně vzdálených od hmotného
středu. Označíme-li
, jak lze přímo zjistit z rovnice
(7,33)
a
(7,34)
. Fyzické kyvadlo kývá se
stejnou dobou kmitu kolem všech rovnoběžných os stejně vzdálených od hmotného
středu. Označíme-li
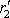 druhý kořen rovnice
(7,35)
, z teorie
kvadratických rovnic (součet kořenů je roven koeficientu u lineárního členu)
plyne
druhý kořen rovnice
(7,35)
, z teorie
kvadratických rovnic (součet kořenů je roven koeficientu u lineárního členu)
plyne
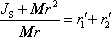 . . |
Jelikož
 , poslední rovnice udává, že součet
, poslední rovnice udává, že součet
 je roven redukované délce
(7,32)
kyvadla, tedy
je roven redukované délce
(7,32)
kyvadla, tedy
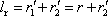 . . |
(7,36) |
Uvažujeme-li pouze osy O a O´ takové, že hmotný střed S
tělesa leží v rovině jimi určené, plyne z rovnice
(7,36)
, že kyvadlo
kýve se stejnou dobou kmitu
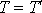 též (kromě výše uvedeného symetrického
případu) kolem dvou os, jejichž vzdálenost je rovna redukované délce kyvadla.
též (kromě výše uvedeného symetrického
případu) kolem dvou os, jejichž vzdálenost je rovna redukované délce kyvadla.
Najdeme-li v tělese dvě rovnoběžné osy nesymetricky vzdálené od hmotného středu, vůči kterým kyvadlo kýve se stejnou dobou kyvu, přičemž hmotný střed leží v rovině určené osami, je vzdálenost os rovna redukované délce fyzického kyvadla.
Jak lze této skutečnosti užít k změření hodnoty tíhového zrychlení g reverzním kyvadlem, je popsáno např.v [17], čl.2.2.2.4. Některé další experimentální aplikace fyzického kyvadla jsou uvedeny v [3].