Mějme izolovanou soustavu hmotných bodů, které všechny mají stejnou rychlost
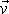 a jejichž celková hmotnost je M. Část soustavy o hmotnosti
a jejichž celková hmotnost je M. Část soustavy o hmotnosti
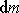 se za čas
se za čas
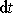 oddělí působením vnitřních sil soustavy a získá rychlost
oddělí působením vnitřních sil soustavy a získá rychlost
 různou od rychlosti
různou od rychlosti
 . Uvažovaný děj vznikne působením vnitřních sil soustavy, soustava jako celek
zůstává izolovanou soustavou hmotných bodů a její hybnost se nemění (viz
čl.5.6).
. Uvažovaný děj vznikne působením vnitřních sil soustavy, soustava jako celek
zůstává izolovanou soustavou hmotných bodů a její hybnost se nemění (viz
čl.5.6).
Celková hybnost soustavy hmotných bodů, dokud se všechny
body pohybují společnou rychlostí
 , je
, je
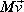 , , |
(7,48) |
kde M je celková hmotnost soustavy. Po rozdělení
soustavy část o hmotnosti
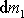 má hybnost
má hybnost
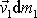 . Hmotnost zbytku soustavy, který se nyní pohybuje společně rychlostí
. Hmotnost zbytku soustavy, který se nyní pohybuje společně rychlostí
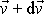 , se změní o
, se změní o
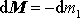 , neboť celková hmotnost soustavy se nemění. Hybnost zbytku (zbytek zde však je
mnohem větší než oddělená část, protože diferenciál dM
budeme pokládat za malou veličinu) soustavy je
, neboť celková hmotnost soustavy se nemění. Hybnost zbytku (zbytek zde však je
mnohem větší než oddělená část, protože diferenciál dM
budeme pokládat za malou veličinu) soustavy je
 . Hybnost celé soustavy i s oddělenou
. Hybnost celé soustavy i s oddělenou
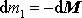 zapíšeme v tvaru
zapíšeme v tvaru
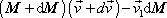 . . |
(7,49) |
Dle zákona zachování hybnosti izolované soustavy musí být (7,48) rovno (7,49) , tedy
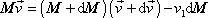 |
(7,50) |
Zanedbáme-li nekonečně malou veličinu druhého řádu
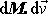 , můžeme rovnici
(7,50)
přepsat na tvar
, můžeme rovnici
(7,50)
přepsat na tvar
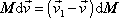 . . |
(7,51) |
Změny hmotnosti a času vztáhneme k časovému intervalu dt, za který se udály, dostaneme
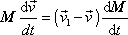 . . |
(7,52) |
Rychlost
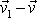 je relativní rychlost oddělené hmotnosti
je relativní rychlost oddělené hmotnosti
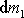 vůči části soustavy, která se společně se pohybuje rychlostí
vůči části soustavy, která se společně se pohybuje rychlostí
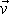 . Relativní rychlost
. Relativní rychlost
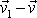 označíme
označíme
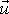 , zrychlení
, zrychlení
 společně se pohybující části soustavy označíme
společně se pohybující části soustavy označíme
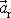 . S těmito symboly můžeme rovnici
(7,52)
přepsat na tvar
. S těmito symboly můžeme rovnici
(7,52)
přepsat na tvar
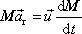 . . |
(7,52) |
Rovnici
(7,52)
jsme zatím odvodili pro případ, kdy ubývá
hmotnosti společně se pohybující části soustavy. Derivace
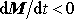 , a tedy relativní rychlost
, a tedy relativní rychlost
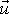 a zrychlení
a zrychlení
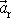 mají opačný smysl.
mají opačný smysl.
Rovnice
(7,52)
však platí i pro případ, kdy
 , tj. pro případ, kdy hmotnost části soustavy se společnou rychlostí roste.
V tomto případě uvažujeme izolovanou soustavu, která na začátku
diferenciálního časového intervalu dt
se skládá z elementární hmotnosti dM
o rychlosti
, tj. pro případ, kdy hmotnost části soustavy se společnou rychlostí roste.
V tomto případě uvažujeme izolovanou soustavu, která na začátku
diferenciálního časového intervalu dt
se skládá z elementární hmotnosti dM
o rychlosti
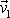 a z části o hmotnosti M
pohybující se rychlostí
a z části o hmotnosti M
pohybující se rychlostí
 a na konci časového intervalu dt
se celá hmotnost soustavy M+dM
pohybuje společnou rychlostí
a na konci časového intervalu dt
se celá hmotnost soustavy M+dM
pohybuje společnou rychlostí
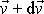 . Ze zákona zachování hybnosti plyne v tomto případě rovnice
. Ze zákona zachování hybnosti plyne v tomto případě rovnice
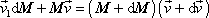 , , |
která je stejná jako rovnice
(7,50)
. Úprava na rovnici
(7,52)
je pak již shodná s úpravou provedenou v předcházejícím
případě, kdy bylo
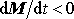 .
.
Rovnice
(7,52)
umožňuje zjistit (ovšem musíme řešit diferenciální rovnici) zrychlení
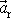 části soustavy, která má rychlost
části soustavy, která má rychlost
 , když známe počáteční hmotnost
, když známe počáteční hmotnost
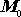 této části soustavy, rychlost
této části soustavy, rychlost
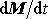 , jakou se její hmotnost mění a relativní rychlost
, jakou se její hmotnost mění a relativní rychlost
 , jakou ji ubývající hmotnost opouští či jakou se k ní přidává. V rovnici
(7,52´)
se vyskytují pouze veličiny, které se vztahují k společně se
pohybující části uvažované soustavy hmotných bodů.
, jakou ji ubývající hmotnost opouští či jakou se k ní přidává. V rovnici
(7,52´)
se vyskytují pouze veličiny, které se vztahují k společně se
pohybující části uvažované soustavy hmotných bodů.
Rovnici
(7,52´)
lze užít k řešení takových problémů,
jako je stanovení pohybu rakety, pohybu kapky padající v prostředí, kde
její hmotnost se zvětšuje kondenzací par, pohybu nádob s vytékající
kapalinou apod. Relativní rychlost
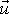 je rychlost, jakou vystřelené plyny
opouštějí raketu počítaná vůči raketě. U kapky je to rychlost, jakou se kapka
pohybuje vůči prostředí, z kterého na ní kondenzují páry. U nádoby
s kapalinou je to výtoková rychlost kapaliny počítaná vůči nádobě.
je rychlost, jakou vystřelené plyny
opouštějí raketu počítaná vůči raketě. U kapky je to rychlost, jakou se kapka
pohybuje vůči prostředí, z kterého na ní kondenzují páry. U nádoby
s kapalinou je to výtoková rychlost kapaliny počítaná vůči nádobě.
Společně se pohybující část
soustavy hmotných bodů je v uvedených příkladech lokalizovaná
v jednou místě. Budeme ji nazývat
systémem s proměnnou hmotností
. Když na takový systém působí ještě vnější síla
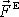 , zrychlení systému
, zrychlení systému
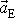 způsobené touto silou,
způsobené touto silou,
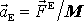 , se přičte k zrychlení
, se přičte k zrychlení
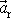 danému rovnicí
(7,52)
. Označíme-li výsledné
zrychlení
danému rovnicí
(7,52)
. Označíme-li výsledné
zrychlení
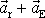 písmenem
písmenem
 , dostáváme pohybovou rovnici systému s proměnou hmotností, tzv.
rovnici Meščerského:
, dostáváme pohybovou rovnici systému s proměnou hmotností, tzv.
rovnici Meščerského:
Výraz
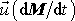 v rovnici
(7,53)
bývá uvažován jako
síla a jedná-li se o případ, kdy
v rovnici
(7,53)
bývá uvažován jako
síla a jedná-li se o případ, kdy
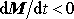 , bývá tato síla nazývána reaktivní silou.
U raket se používá též názvu tažná síla.
, bývá tato síla nazývána reaktivní silou.
U raket se používá též názvu tažná síla.
Uvedeme některé závěry o pohybu raket. Pro jednoduchost
zanedbáme vliv vnější síly
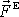 , vyjdeme tedy z rovnice
(7,52)
. Předpokládáme-li stálou rychlost úbytku
hmotnosti
, vyjdeme tedy z rovnice
(7,52)
. Předpokládáme-li stálou rychlost úbytku
hmotnosti
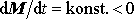 a stálou relativní rychlost
a stálou relativní rychlost
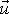 zplodin hoření vystřelovaných z rakety,
plyne z rovnice
(7,52´)
, že
zplodin hoření vystřelovaných z rakety,
plyne z rovnice
(7,52´)
, že
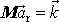 , kde
, kde
 je konstantní vektor. Jelikož hmotnost rakety
s časem ubývá, zrychlení rakety
je konstantní vektor. Jelikož hmotnost rakety
s časem ubývá, zrychlení rakety
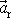 za uvedených podmínek s časem roste.
Vyjdeme-li z rovnice
(7,52)
, přesněji z původního tvaru
(7,51)
,
můžeme určit velikost konečné rychlosti rakety
za uvedených podmínek s časem roste.
Vyjdeme-li z rovnice
(7,52)
, přesněji z původního tvaru
(7,51)
,
můžeme určit velikost konečné rychlosti rakety
 , známe-li hmotnost
, známe-li hmotnost
 rakety před startem, velikost relativní rychlosti u
vystřelovaných plynů a konečnou hmotnost
rakety před startem, velikost relativní rychlosti u
vystřelovaných plynů a konečnou hmotnost
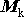 rakety po vyhoření veškerého paliva.
Podrobný výpočet provedený např. v [20], kap.6 dává
rakety po vyhoření veškerého paliva.
Podrobný výpočet provedený např. v [20], kap.6 dává
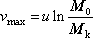 . . |
(7,54) |
Poměr
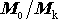 , na kterém dosažená konečná rychlost rakety podstatně závisí, se nazývá
Ciolkovského číslo.
, na kterém dosažená konečná rychlost rakety podstatně závisí, se nazývá
Ciolkovského číslo.
Rovnice
(7.54)
platí i pro výpočet zvýšení rychlosti
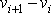 vyhořením
vyhořením
 -tého stupně vícestupňové rakety. Stačí nahradit výraz
-tého stupně vícestupňové rakety. Stačí nahradit výraz
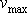 na levé straně rovnice
(7.54)
rozdílem rychlostí
na levé straně rovnice
(7.54)
rozdílem rychlostí
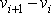 . Hmotnost
. Hmotnost
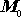 v tomto případě značí hmotnost před
zažehnutím uvažovaného stupně rakety a
v tomto případě značí hmotnost před
zažehnutím uvažovaného stupně rakety a
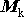 hmotnost po jeho vyhoření.
hmotnost po jeho vyhoření.