Jako ráz těles můžeme též hovořit o srážkách těles se označuje krátkodobý děj interakce dvou těles, při kterém dochází k náhlým změnám vektorů rychlostí hmotných středů obou těles i vektorů jejich úhlových rychlostí. Interakční síly, říkáme jim v této souvislosti též nárazové síly, odpovídají rychlým změnám vektorů rychlosti, tj. velkým zrychlením, a jsou tedy velké. Detailní průběh těchto sil závisí na reologických (viz II.2) vlastnostech těles, jejich tvaru a způsobu, jakým ke střetu došlo. Pro předávání momentů hybnosti jsou navíc důležité i kluzné (třecí) vlastnosti povrchů. Při rázu těles často dochází k nevratným změnám jejich tvaru, takže potom i aproximace děje představou střetu dvou tuhých těles selhává. Pro nalezení hlavních charakteristik rázů je tedy nutné děje vhodným způsobem schematizovat a teprve tato zjednodušená schémata podrobit analýze.
Předpokládáme, že tělesa se na počátku rázu dotknou v jediném bodě, který se nazývá bod rázu. Tímto bodem vedeme společnou tečnou rovinu obou těles a bodem rázu kolmici (normálu) k této rovině Leží-li hmotné středy obou těles na této kolmici, nazývá se ráz středový, v opačném případě se jedná o ráz výstředný. Jsou-li obě tělesa účastnící se rázu homogenní koule, je zaručeno, že ráz bude středový. Pohybují-li se těžiště obou těles před rázem po normále k budoucímu bodu rázu, je ráz přímý, pro opačný případ se užívá označení ráz šikmý.
Reologické chování (viz II.2) těles při rázu se schematizuje dvěma krajními modely, tělesa se pokládají buď za dokonale pružná nebo za dokonale nepružná. Uvažuje se i případ mezi těmito krajními modely, kdy tělesa jsou nedokonale pružná. Dokonale pružný ráz užívá se i zkrácené označení pružný ráz se uvažuje jako ráz, v jehož průběhu se kinetická energie těles zachovává, tedy součet kinetických energií těles před rázem je roven součtu kinetických energií těles po rázu. Dokonale nepružný ráz užívá se též zkrácené označení nepružný ráz se uvažuje jako ráz, v jehož průběhu se obě tělesa spojí a po rázu se pohybují jako jedno těleso, jehož hmotnost je rovna součtu hmotností původních dvou těles. Při nedokonale pružném rázu se tělesa při rázu od sebe odrazí, ale součet jejich kinetických energií po rázu je menší než před rázem.
Při vyšetřování rázu těles nesledujeme detailní průběh interakčních sil, ale určujeme pouze jejich výsledný impuls, který zjistíme z rozdílu hybností jednotlivých těles před rázem a po rázu. Z takto zjištěného impulsu interakční síly můžeme určit její průměrnou velikost, když známe dobu trvání rázu.
Interakční síly jsou vnitřními silami soustavy těles účastnících se rázu, a proto jejich působením se celková hybnost a celkový moment hybnosti soustavy nemění. Pro ráz tedy platí jak zákon zachování hybnosti (5,52) tak zákon zachování momentu hybnosti (5,61) . Pro ráz dvou těles můžeme tyto zákony (když zanedbáme vzhledem ke krátkému působení rázu nepatrný impuls vnějších sil, např. tíhy), vyslovit v tvaru:
1. Vektorový součet hybností obou těles po rázu je roven jejich vektorovému součtu před rázem.
2. Vektorový součet momentů hybnosti soustavy obou těles po rázu je roven vektorovému součtu momentů hybnosti soustavy těles před rázem.
V druhém zákonu si však musíme jasně uvědomit, že vektorový součet momentů hybnosti soustavy dvou těles se skládá ze čtyř členů: dvou momentů hybnosti těles vůči svým těžištím (vlastních momentů hybnosti těles) a dvou momentů hybnosti těžišť těles vůči bodu, ke kterému moment hybnosti počítáme. Tento bod musí být stejný pro výpočet momentu hybnosti soustavy před rázem a po rázu. Můžeme za něj volit např. bod rázu.
Z uvedeného vyplývá, že i tělesa, která se před rázem netočí (mají nulový vlastní moment hybnosti), se po rázu obvykle roztočí, když před rázem součet momentů hybnosti jejich těžišť vůči bodu rázu je nenulový. Taková situace často nastane při srážce aut.
Vyslovené dva zákony určují šest z dvanácti stupňů volnosti pohybu dvou těles po rázu. Je-li ráz dokonale pružný, přibude ještě jedna rovnice určující zákon zachování mechanické energie, ale stejně zůstane úloha o rázu v přiblížení srážky dvou tuhých těles úlohou neurčitou, která k jednoznačnosti řešení potřebuje udání ještě dalších podmínek.
Obvykle při vyšetřování schémat rázu uvažujeme pouze postupný pohyb. I potom však zákon zachování hybnosti určí pouze tři ze šesti stupňů volnosti postupného pohybu dvou tuhých těles po rázu a i pro dokonale pružný ráz, kde přibude určení jednoho stupně volnosti ze zákona zachování mechanické energie, zůstane úloha bez udání dalších podmínek neurčitou. Některé obecné zákonitosti však o takových rázech lze vyslovit. Podrobnější rozbor tohoto typu rázu, kterým se mimo jiné popisují srážky elementárních částic, podáme ve stati 7.1.1.
Jednoznačně lze vyřešit nepružný ráz a pružný ráz vázaný na přímku v přiblížení postupného pohybu, tedy jako srážky dvou hmotných bodů. Řešení nedokonale pružných rázů a rázů s uvážením rotace těles je obtížné. Některé závěry lze nalézt v učebnici [3], jejíž hlavní autor prof. Horák se problematikou rázů podrobně zabýval.
 Při vyšetřování srážek elementárních částic
pokládáme tyto částice za hmotné body
Při vyšetřování srážek elementárních částic
pokládáme tyto částice za hmotné body
Potřebujeme-li uvažovat o rotaci, zavádíme pojem spinu.
V čl.5.4 jsme probrali některé zvláštní případy srážek dvou hmotných bodů, na které nepůsobí vnější síly. Odvodili jsme i základní rovnici
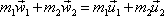 |
(5,54) |
vyjadřující zákon zachování hybnosti uvažované izolované soustavy dvou hmotných bodů. Vyšetřovali jsme však jen takové srážky, kdy celý pohyb bylo možno redukovat na jednorozměrný problém.
Nyní rozšíříme úvahy na
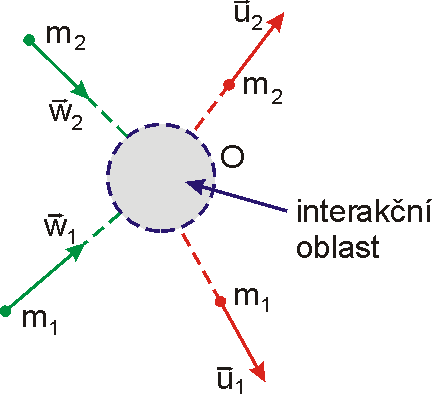
trojrozměrný případ. Mějme dva hmotné body
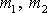 , které se do oblasti vzájemného působení (interakce) na obr. 80 označené jako O
blíží rychlostmi
, které se do oblasti vzájemného působení (interakce) na obr. 80 označené jako O
blíží rychlostmi
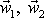 . Po vzájemném působení (srážce) se hmotné body rozletí rychlostmi
. Po vzájemném působení (srážce) se hmotné body rozletí rychlostmi
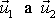 . Dále budeme předpokládat, že se srážkou nezmění celková mechanická energie
soustavy dvou hmotných bodů. V prostoru mimo oblast vzájemného působení
můžeme mechanickou energii soustavy pokládat za součet kinetických energií obou
hmotných bodů. Podmínka zachování mechanické energie je pak vyjádřena rovnicí
. Dále budeme předpokládat, že se srážkou nezmění celková mechanická energie
soustavy dvou hmotných bodů. V prostoru mimo oblast vzájemného působení
můžeme mechanickou energii soustavy pokládat za součet kinetických energií obou
hmotných bodů. Podmínka zachování mechanické energie je pak vyjádřena rovnicí
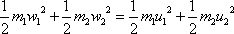 . . |
(7,1) |
Jak jsme uvedli v úvodu článku, srážce, při které se zachovává mechanická energie soustavy, říkáme pružná srážka.
Známe-li pohyb hmotných bodů před srážkou, jsou rovnicemi (5,54) a (7,1) stanoveny čtyři podmínky pro šest stupňů volnosti pohybu dvou hmotných bodů po srážce. Rovnicemi (5,54) a (7,1) nelze tedy problém pružné srážky dvou hmotných bodů zcela rozřešit. K úplnému řešení je třeba znát kromě pohybu hmotných bodů před srážkou i charakter sil, kterými body na sebe působí v interakční oblasti O. Pružná srážka dvou hmotných bodů je podmínkami (5,54) a (7,1) natolik omezena, že některé obecné závěry o jejím výsledku můžeme zjistit, aniž známe průběh silového působení v oblasti O.
Těžišťová soustava souřadná
Nejsnáze lze srážku dvou hmotných bodů popsat
v soustavě souřadné, v níž těžiště hmotných bodů je v klidu
takové soustavě souřadné říkáme těžišťová.
Soustavu hmotných bodů
pokládáme za izolovanou; hmotný střed soustavy je buď v klidu nebo
v rovnoměrném přímočarém pohybu. Těžišťová soustava souřadná je tedy
jednou z inerciálních soustav souřadných a můžeme ji užít k popisu
pohybu, aniž bychom museli uvažovat o působení nějakých zdánlivých sil.
V těžišťové soustavě souřadné je hybnost soustavy (viz rovnici
(5,73)
)
hmotných bodů nulová. Rychlosti hmotných bodů v těžišťové soustavě před
srážkou označíme
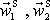 a po srážce
a po srážce
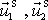 . V těžišťové soustavě souřadné nejen platí rovnice typu
(5,54)
, ale navíc
obě strany rovnice jsou nulové, tedy
. V těžišťové soustavě souřadné nejen platí rovnice typu
(5,54)
, ale navíc
obě strany rovnice jsou nulové, tedy
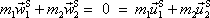 . . |
(5,54) |
Rovnice, která vyjadřuje zachování mechanické energie soustavy, má v těžišťové soustavě souřadné tvar
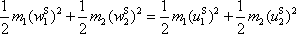 . . |
(7,1) |
Výraz
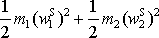 má obecně jinou hodnotu než výraz
má obecně jinou hodnotu než výraz
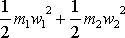 . Z rovnice
(5,54´)
plyne, že jak hybnosti
. Z rovnice
(5,54´)
plyne, že jak hybnosti
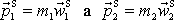 hmotných bodů před srážkou, tak hybnosti
hmotných bodů před srážkou, tak hybnosti
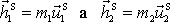 hmotných bodů po srážce jsou stejně velké,
stejného směru a opačného smyslu. Hybnosti
hmotných bodů po srážce jsou stejně velké,
stejného směru a opačného smyslu. Hybnosti
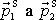 směřují k oblasti interakce
(srážky) O, hybnosti
směřují k oblasti interakce
(srážky) O, hybnosti
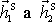 míří od oblasti O (viz obr.81). Z rovnice
(5,54´)
pro absolutní hodnoty hybností plynou rovnice
míří od oblasti O (viz obr.81). Z rovnice
(5,54´)
pro absolutní hodnoty hybností plynou rovnice
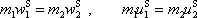 , , |
a tedy
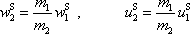 . . |
Dosadíme-li právě získané vyjádření
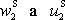 do rovnice
(7,1)
, dostáváme po úpravě
do rovnice
(7,1)
, dostáváme po úpravě
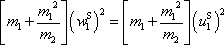 , , |
odkud plyne
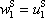 . . |
(7,2) |
Velikost rychlosti hmotného bodu
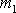 před srážkou je rovna velikosti jeho
rychlosti po srážce. Podobně lze dokázat, že i velikost rychlosti druhého
hmotného bodu se srážkou nezmění, tedy
před srážkou je rovna velikosti jeho
rychlosti po srážce. Podobně lze dokázat, že i velikost rychlosti druhého
hmotného bodu se srážkou nezmění, tedy
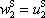 . . |
(7,3) |
Z rovnic
(5,54)
,
(7,2)
a
(7,3)
plyne, že všechny hybnosti
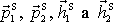 mají stejnou velikost, jak již bylo
zakresleno na obr.81. Velikosti rychlostí hmotných bodů po srážce jsou tedy
podmínkami
(5,54)
a
(7,1)
určeny. Zbývá určit jejich směr.
mají stejnou velikost, jak již bylo
zakresleno na obr.81. Velikosti rychlostí hmotných bodů po srážce jsou tedy
podmínkami
(5,54)
a
(7,1)
určeny. Zbývá určit jejich směr.
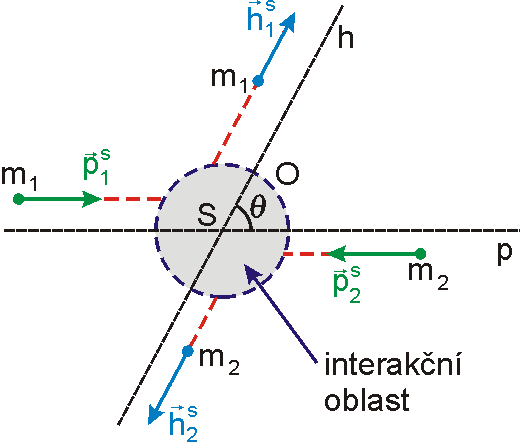 Jak je
naznačeno na obr.81, v obecném případě se hmotné body před interakcí
pohybují po dvou rovnoběžkách. Rovnoběžky určují rovinu a směr pohybu hmotných
bodů před interakcí (srážkou). Je třeba určit pohyb bodů po srážce, jak
vzhledem k této rovině, tak i vzhledem k původnímu směru pohybu
hmotných bodů. K tomu je třeba dvou údajů (úhlů), jak odpovídá dvěma dosud
neurčeným stupňům volnosti pohybu hmotných bodů po srážce. Zpravidla předpokládáme,
že působení mezi hmotnými body je dáno centrálními silami a potom, jak jsme
ukázali v článku 4.3 (viz též čl.5.6), zůstává zachována rovina pohybu.
Obrázek 81 lze pak chápat jako rovinný obrazec a k určení pohybu po
srážce stačí udat úhel
Jak je
naznačeno na obr.81, v obecném případě se hmotné body před interakcí
pohybují po dvou rovnoběžkách. Rovnoběžky určují rovinu a směr pohybu hmotných
bodů před interakcí (srážkou). Je třeba určit pohyb bodů po srážce, jak
vzhledem k této rovině, tak i vzhledem k původnímu směru pohybu
hmotných bodů. K tomu je třeba dvou údajů (úhlů), jak odpovídá dvěma dosud
neurčeným stupňům volnosti pohybu hmotných bodů po srážce. Zpravidla předpokládáme,
že působení mezi hmotnými body je dáno centrálními silami a potom, jak jsme
ukázali v článku 4.3 (viz též čl.5.6), zůstává zachována rovina pohybu.
Obrázek 81 lze pak chápat jako rovinný obrazec a k určení pohybu po
srážce stačí udat úhel
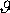 , kte-rý svírá přímka h s přímkou p. Přímka p
je přímka prolo-žená hmotným středem S ve
směru pohybu hmotných bodů před srážkou a přímka h
je proložená hmotným středem ve směru pohybu
hmotných bodů po srážce. V přibližném vyjádření, kdy oblast O poklá-dáme
za bodovou, předpo-kládáme, že body před sráž-kou se pohybují přesně podél
přímky p a po srážce podél
přímky h. V tomto přiblížení také stačí udání úhlu
, kte-rý svírá přímka h s přímkou p. Přímka p
je přímka prolo-žená hmotným středem S ve
směru pohybu hmotných bodů před srážkou a přímka h
je proložená hmotným středem ve směru pohybu
hmotných bodů po srážce. V přibližném vyjádření, kdy oblast O poklá-dáme
za bodovou, předpo-kládáme, že body před sráž-kou se pohybují přesně podél
přímky p a po srážce podél
přímky h. V tomto přiblížení také stačí udání úhlu
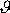 mezi přímkami h a p
určení pohybu hmotných bodů po srážce. Dále budeme vždy
předpokládat srážky takového druhu, kdy úhel
mezi přímkami h a p
určení pohybu hmotných bodů po srážce. Dále budeme vždy
předpokládat srážky takového druhu, kdy úhel
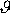 plně určuje směr pohybu hmotných bodů po srážce.
plně určuje směr pohybu hmotných bodů po srážce.
Známe-li centrální síly působící mezi hmotnými body, lze
řešením problému dvou těles (viz čl.5.6) stanovit úhel
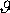 v závislosti na vzdálenosti hmotných
bodů od přímky p před srážkou. Důležitou
úlohou je stanovit průměrné rozdělení úhlu
v závislosti na vzdálenosti hmotných
bodů od přímky p před srážkou. Důležitou
úlohou je stanovit průměrné rozdělení úhlu
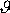 , dopadá-li více hmotných bodů, nebo jak v této souvislosti říkáme částic,
na zvolený hmotný bod. Mluvíme pak o rozptylu částic. Stanovení úhlů
, dopadá-li více hmotných bodů, nebo jak v této souvislosti říkáme částic,
na zvolený hmotný bod. Mluvíme pak o rozptylu částic. Stanovení úhlů
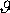 i jejich rozdělení pro různé druhy
centrálních silových polí je diskutováno např. v [11], [12].
i jejich rozdělení pro různé druhy
centrálních silových polí je diskutováno např. v [11], [12].
Zde rozebereme pouze závěry, které lze o pružné srážce dvou
hmotných bodů učinit, neznáme-li úhel
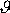 .
V článku 5.6 jsme ukázali (viz rovnici
(5,83)
), že rychlosti dvou hmotných
bodů tvořící soustavu lze v těžišťové soustavě souřadné vyjádřit dle
jejich vzájemné rychlosti. Můžeme tedy psát
.
V článku 5.6 jsme ukázali (viz rovnici
(5,83)
), že rychlosti dvou hmotných
bodů tvořící soustavu lze v těžišťové soustavě souřadné vyjádřit dle
jejich vzájemné rychlosti. Můžeme tedy psát
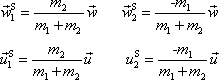 , , |
kde
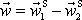 je vzájemná rychlost hmotných bodů před
srážkou a
je vzájemná rychlost hmotných bodů před
srážkou a
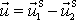 jejich vzájemná rychlost po srážce.
Z rovnic
(7,2)
a
(7,3)
, uvážíme-li, že jak rychlosti
jejich vzájemná rychlost po srážce.
Z rovnic
(7,2)
a
(7,3)
, uvážíme-li, že jak rychlosti
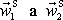 , tak i rychlosti
, tak i rychlosti
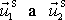 mají stejný směr a opačný smysl, plyne
rovnost velikosti vektorů
mají stejný směr a opačný smysl, plyne
rovnost velikosti vektorů
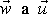 ;
;
 |
(7,6) |
Rychlosti hmotných bodů po srážce můžeme pak vyjádřit jako
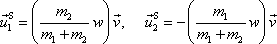 . . |
(7,7) |
V rovnicích
(7,7)
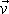 je jednotkový vektor ve směru pohybu
hmotných bodů po srážce; smysl vektoru
je jednotkový vektor ve směru pohybu
hmotných bodů po srážce; smysl vektoru
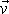 je shodný se smyslem vektoru
je shodný se smyslem vektoru
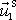 . Těžišťová soustava souřadná se vůči původní soustavě souřadné pohybuje rychlostí
. Těžišťová soustava souřadná se vůči původní soustavě souřadné pohybuje rychlostí
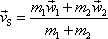 , , |
(7,8) |
tj. rychlostí, jakou má hmotný střed v původní soustavě souřadné (viz například rovnici (5,54) ). Vztah mezi rychlostmi hmotných bodů v původní a těžišťové soustavě je dán rovnicemi
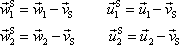 . . |
(7,9) |
Pro rychlosti
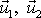 získáme pak dle
(7,9)
,
(7,7)
a
(7,8)
vyjádření
získáme pak dle
(7,9)
,
(7,7)
a
(7,8)
vyjádření
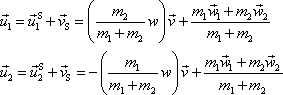 . . |
(7,10) |
Rovnice
(7,10)
určují rychlosti hmotných bodů po srážce na
základě údajů, které s výjimkou směru
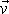 lze určit z rychlostí hmotných bodů před srážkou. Rovnice
(7,10)
platí v libovolné inerciální soustavě souřadné, která se vůči těžišťové
soustavě pohybuje rychlostí
lze určit z rychlostí hmotných bodů před srážkou. Rovnice
(7,10)
platí v libovolné inerciální soustavě souřadné, která se vůči těžišťové
soustavě pohybuje rychlostí
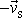 . Přitom rychlost
. Přitom rychlost
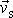 určená rovnicí
(7,8)
je pro různé soustavy souřadné různá.
určená rovnicí
(7,8)
je pro různé soustavy souřadné různá.
Abychom mohli snáze podat geometrickou interpretaci rovnice
(7,10)
, převedeme ji na rovnici mezi hybnostmi
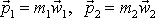 hmotných bodů před srážkou a hybnostmi
hmotných bodů před srážkou a hybnostmi
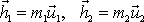 hmotných bodů po srážce. Vynásobíme-li první
z rovnic
(7,10)
hmotností
hmotných bodů po srážce. Vynásobíme-li první
z rovnic
(7,10)
hmotností
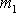 prvého hmotného bodu a druhou z rovnic
(7,10)
hmotností
prvého hmotného bodu a druhou z rovnic
(7,10)
hmotností
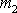 druhého hmotného bodu, dostaneme
druhého hmotného bodu, dostaneme
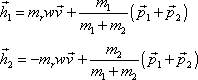 . . |
(7,11) |
V rovnici
(7,11)
jsme výraz
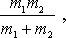 který dle
(5,88)
nazýváme redukovanou hmotností, označili
který dle
(5,88)
nazýváme redukovanou hmotností, označili
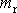 . Vektor
. Vektor
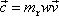 |
(7,12) |
má konstantní velikost a libovolný směr. Umístíme-li počátek vektoru
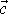 do středu S kružnice, leží jeho konec na kružnici (viz obr.82). Vektor
do středu S kružnice, leží jeho konec na kružnici (viz obr.82). Vektor
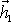 je součtem vektoru
je součtem vektoru
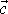 a vektoru
a vektoru
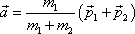 . . |
(7,13) |
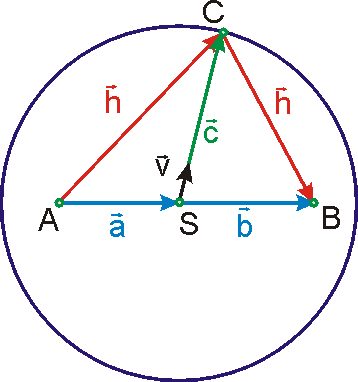 Umístíme-li konec vektoru
Umístíme-li konec vektoru
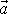 do středu S kružnice, vektor
do středu S kružnice, vektor
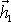 míří od počátku vektoru
míří od počátku vektoru
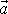 ke konci vektoru
ke konci vektoru
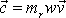 . Vektor
. Vektor
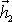 získáme, odečteme-li vektor
získáme, odečteme-li vektor
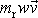 od vektoru
od vektoru
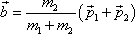 , , |
(7,14) |
což lze graficky provést, položíme-li počátek vektoru
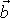 do středu S kružnice a spojíme konce
vektorů
do středu S kružnice a spojíme konce
vektorů
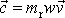 a
a
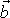 . Vektory
. Vektory
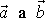 jsou zřejmě rovnoběžné.
jsou zřejmě rovnoběžné.
Obě popsané konstrukce jsou souhrnně znázor-něny na obr.82.
Obrázek 82 tak dává rychlou grafickou metodou, dle níž lze pro libovolně
zvolený směr
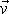 určit hybnosti
určit hybnosti
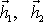 hmotných bodů po srážce při známých hybnostech
hmotných bodů po srážce při známých hybnostech
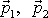 hmotných bodů před srážkou.
hmotných bodů před srážkou.
Laboratorní soustava souřadná
Mezi netěžišťovými souřadnými soustavami je významná
soustava, v níž jeden z hmotných bodů je před srážkou v klidu.
Takové soustavě souřadné říkáme laboratorní,
neboť zpravidla ji
užíváme k vyšetřování srážek, při kterých bod před srážkou klidný je též
klidný vůči laboratoři. Takové omezení není obecně nutné a laboratorní soustavu
souřadnou lze nalézt pro každou srážku dvou izolovaných hmotných bodů, neboť
existuje neinerciální soustava souřadná, v které jeden z hmotných
bodů (můžeme si dokonce vybrat, kterému z hmotnému bodu chceme laboratorní
soustavu přiřadit) je před srážkou v klidu.
Dále budeme předpokládat, že v laboratorní soustavě
souřadné je před srážkou v klidu druhý hmotný bod
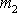 . Označíme-li veličiny vztahující se k laboratorní soustavě indexem L,
budeme tedy předpokládat, že hybnost
. Označíme-li veličiny vztahující se k laboratorní soustavě indexem L,
budeme tedy předpokládat, že hybnost
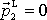 . Z rovnice
(7,14)
potom plyne, že vektor
. Z rovnice
(7,14)
potom plyne, že vektor
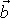 má v laboratorní soustavě souřadné velikost
má v laboratorní soustavě souřadné velikost
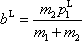 . . |
V laboratorní soustavě souřadné velikost vzájemné
rychlosti částic
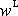 je rovna velikosti rychlosti první
částice
je rovna velikosti rychlosti první
částice
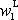 . Rozepíšeme-li výraz pro redukovanou hmotnost,
. Rozepíšeme-li výraz pro redukovanou hmotnost,
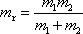 , , |
dostáváme potom z rovnice
(7,12)
pro velikost vektoru
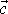 v laboratorní soustavě souřadné vyjádření
v laboratorní soustavě souřadné vyjádření
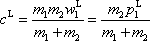 , , |
a tedy
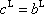 . . |
(7,15) |
V laboratorní soustavě souřadné nejen bod C, ale i bod B leží na kružnici v grafickém vyjádření daném obrázkem 82.
Obrázek 82 pro speciální případ laboratorní soustavy souřadné je zakreslen na obr.83. Vektor
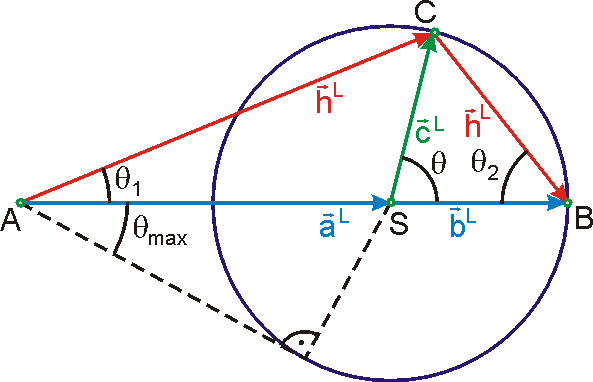
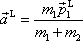 |
(7,16) |
a vektor
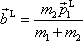 . . |
(7,17) |
V laboratorní soustavě jsou vektory
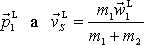 rovnoběžné, a proto úhel
rovnoběžné, a proto úhel
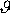 naznačený na obr.83 je úhlem
naznačený na obr.83 je úhlem
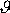 z obr.81, tj. úhlem, o který se srážkou
změní směr pohybu hmotných bodů v těžišťové soustavě souřadné. Na obr.83
je znázorněn též úhel
z obr.81, tj. úhlem, o který se srážkou
změní směr pohybu hmotných bodů v těžišťové soustavě souřadné. Na obr.83
je znázorněn též úhel
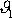 , o který se odchýlí po srážce směr pohybu prvého hmotného bodu od jeho směru
před srážkou a úhel
, o který se odchýlí po srážce směr pohybu prvého hmotného bodu od jeho směru
před srážkou a úhel
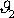 , který svírá směr pohybu druhého hmotného bodu po srážce se směrem pohybu
prvního hmotného bodu před srážkou.
, který svírá směr pohybu druhého hmotného bodu po srážce se směrem pohybu
prvního hmotného bodu před srážkou.
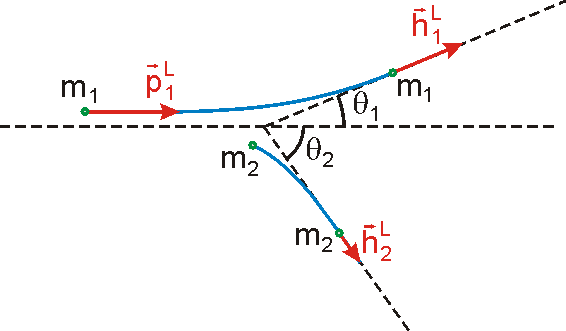
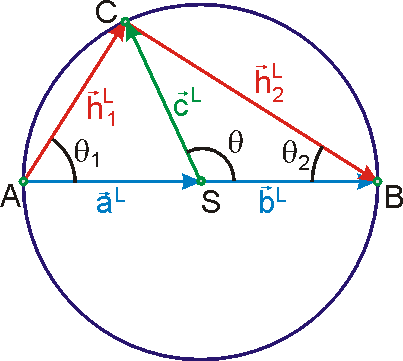
Význam úhlů
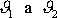 zřetelně plyne z obrázku 84, na kterém
je zakreslena srážka odpovídající případu znázorněnému na obr.83. Vektory
zřetelně plyne z obrázku 84, na kterém
je zakreslena srážka odpovídající případu znázorněnému na obr.83. Vektory
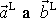 jsou dle
(7,16)
a
(7,17)
rovnoběžné
s vektorem
jsou dle
(7,16)
a
(7,17)
rovnoběžné
s vektorem
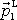 . Aby obrázek 84 nemusel být příliš veliký,
jsou na něm velikosti vektorů čtyřikrát zmenšeny oproti grafu 83. Porovnáním
rovnic
(7,16)
a
(7,17)
zjistíme, že velikosti vektorů
. Aby obrázek 84 nemusel být příliš veliký,
jsou na něm velikosti vektorů čtyřikrát zmenšeny oproti grafu 83. Porovnáním
rovnic
(7,16)
a
(7,17)
zjistíme, že velikosti vektorů
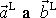 jsou v poměru
jsou v poměru
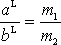 a obr.83 tedy odpovídá případu, kdy
a obr.83 tedy odpovídá případu, kdy
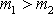 . V tomto případě úhel
. V tomto případě úhel
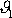 nemůže nabýt libovolných hodnot. Jeho maximální hodnota je dána podmínkou
nemůže nabýt libovolných hodnot. Jeho maximální hodnota je dána podmínkou
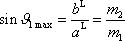 , , |
(7,18) |
jak lze snadno vyčíst z obr.83.
Má-li hmotný bod, který je před srážkou v klidu vůči
laboratorní soustavě souřadné, menší hmotnost než dopadající hmotný bod, může
se dopadající hmotný bod odchýlit od směru své původní dráhy nejvýše o
úhel
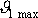 daný rovnicí
(7,18)
. Toto tvrzení můžeme
vyslovit, aniž známe charakter sil působících mezi oběma hmotnými body. Má-li
před srážkou klidný bod větší hmotnost než dopadající hmotný bod, tedy platí-li
nerovnost
daný rovnicí
(7,18)
. Toto tvrzení můžeme
vyslovit, aniž známe charakter sil působících mezi oběma hmotnými body. Má-li
před srážkou klidný bod větší hmotnost než dopadající hmotný bod, tedy platí-li
nerovnost
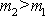 , žádné omezení typu
(7,18)
pro úhel
, žádné omezení typu
(7,18)
pro úhel
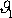 neplatí. Bod A na grafu 83 leží uvnitř
kružnice, jak plyne z úměry
neplatí. Bod A na grafu 83 leží uvnitř
kružnice, jak plyne z úměry
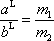 , , |
když
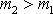 .
.
 Najdeme vztah mezi úhly
Najdeme vztah mezi úhly
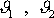 a úhlem
a úhlem
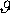 . Z obr.83 lze vyčíst, že
. Z obr.83 lze vyčíst, že
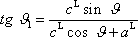 . . |
Dle
(7,15)
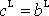 a dosadíme-li za
a dosadíme-li za
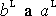 dle
(7,17)
a
(7,16)
, dostaneme
dle
(7,17)
a
(7,16)
, dostaneme
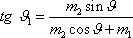 . . |
(7,19) |
Trojúhelník BSC z obr.83 je rovnoramenný, a tedy
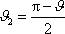 . . |
(7,20) |
 Je-li
Je-li
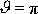 , je vždy
, je vždy
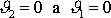 , když
, když
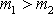 a
a
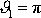 , když
, když
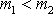 (viz též obr.83). Pro centrální síly nastává případ
(viz též obr.83). Pro centrální síly nastává případ
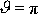 , když hmotné body se před srážkou pohybují přesně ve směru své spojnice Po
srážce zachovávají oba hmotné body původní směr pohybu. Hmotný bod
, když hmotné body se před srážkou pohybují přesně ve směru své spojnice Po
srážce zachovávají oba hmotné body původní směr pohybu. Hmotný bod
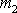 , který je před srážkou v klidu, se po srážce pohybuje ve stejném smyslu
jako hmotný bod
, který je před srážkou v klidu, se po srážce pohybuje ve stejném smyslu
jako hmotný bod
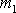 před srážkou. Bod
před srážkou. Bod
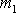 se po srážce pohybuje ve stejném smyslu jako
před srážkou, když
se po srážce pohybuje ve stejném smyslu jako
před srážkou, když
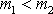 a v opačném smyslu než před srážkou,
když
a v opačném smyslu než před srážkou,
když
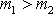 . Pružnou srážku dvou hmotných bodů, které před srážkou se pohybují podél přímky
a zůstanou v pohybu podél této přímky i po srážce, lze úplně rozřešit
elementárními prostředky. Pro jedno-rozměrný případ jsou totiž rovnice
(5,54)
a
(7,1)
dvěma rovnicemi k určení dvou stupňů volnosti, které mají hmotné
body po srážce.
. Pružnou srážku dvou hmotných bodů, které před srážkou se pohybují podél přímky
a zůstanou v pohybu podél této přímky i po srážce, lze úplně rozřešit
elementárními prostředky. Pro jedno-rozměrný případ jsou totiž rovnice
(5,54)
a
(7,1)
dvěma rovnicemi k určení dvou stupňů volnosti, které mají hmotné
body po srážce.
Vyšetříme nyní v laboratorní
soustavě souřadné pružnou srážku dvou stejně těžkých hmotných bodů.
Z podmínky
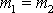 plyne dle
(7,16)
a
(7,17)
, že velikosti vektorů
plyne dle
(7,16)
a
(7,17)
, že velikosti vektorů
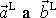 jsou stejné, tedy
jsou stejné, tedy
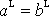 . Na kružnici grafu 83 leží nejen body C a B, ale i bod A, jak je naznačeno na
obr.85. Užitím elementárních geometrických vztahů plyne z obrázku 85, že
. Na kružnici grafu 83 leží nejen body C a B, ale i bod A, jak je naznačeno na
obr.85. Užitím elementárních geometrických vztahů plyne z obrázku 85, že
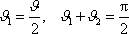 . . |
(7,21) |
Narazí-li na hmotný bod
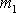 stejně těžký hmotný bod
stejně těžký hmotný bod
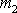 , po srážce se oba stejně těžké hmotné body rozletí a pohybují se ve směrech,
které spolu svírají pravý úhel.
, po srážce se oba stejně těžké hmotné body rozletí a pohybují se ve směrech,
které spolu svírají pravý úhel.
Takto probíhá srážka s výjimkou případu, kdy
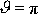 . Je-li
. Je-li
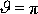 , musí se hmotné body po srážce pohybovat ve stejné přímce jako bod
, musí se hmotné body po srážce pohybovat ve stejné přímce jako bod
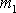 před srážkou. Rovnice
(5,54)
a
(7,1)
mají
pro laboratorní soustavu souřadnou tvar:
před srážkou. Rovnice
(5,54)
a
(7,1)
mají
pro laboratorní soustavu souřadnou tvar:
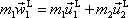 |
a
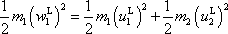 . . |
V uvažovaném jednorozměrném případě srážky dvou
hmotných bodů o stejné hmotnosti
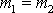 můžeme rovnice zjednodušit a dostaneme
můžeme rovnice zjednodušit a dostaneme
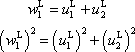 . . |
(7,22) |
V první rovnici jsou
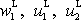 vektory rychlosti v přímce, tedy
veličiny, které mohou být jak kladné tak záporné. Umocníme-li první
z rovnic
(7,22)
na druhou a odečteme druhou rovnici, získáme podmínku
vektory rychlosti v přímce, tedy
veličiny, které mohou být jak kladné tak záporné. Umocníme-li první
z rovnic
(7,22)
na druhou a odečteme druhou rovnici, získáme podmínku
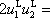 |
(7,23) |
0 .
Z podmínky
(7,23)
plyne, že rovnice
(7,22)
mohou společně platit pouze, když bude
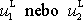 nulové. Položíme-li
nulové. Položíme-li
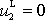 , je dle první rovnice
(7,22)
, je dle první rovnice
(7,22)
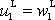 , což odpovídá případu, kdy k žádné srážce nedojde. Zbývá tedy položit
, což odpovídá případu, kdy k žádné srážce nedojde. Zbývá tedy položit
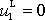 . Pak z první rovnice
(7,22)
dostáváme
. Pak z první rovnice
(7,22)
dostáváme
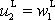 . Po srážce se první hmotný bod zastaví a druhý se pohybuje dále stejnou
rychlostí, jakou měl první hmotný bod před srážkou. Říkáme, že hmotné body si
vymění rychlosti. Uvedený výsledek je ve shodě s grafem 85.
. Po srážce se první hmotný bod zastaví a druhý se pohybuje dále stejnou
rychlostí, jakou měl první hmotný bod před srážkou. Říkáme, že hmotné body si
vymění rychlosti. Uvedený výsledek je ve shodě s grafem 85.
Výměnu rychlostí lze dobře demonstrovat při srážce stejně těžkých homogenních koulí, z nichž jedna je původně v klidu. Musíme však zajistit, aby hmotný střed narážející koule se před srážkou pohyboval po přímce, která prochází hmotným středem klidné koule a nesmíme připustit rotaci koulí.