 V čl. 6.4 jsme zavedli název těžký
setrvačník pro těleso otáčející se v tíhovém poli kolem bodu, který není
hmotným středem tělesa. Přehled případů, kdy lze podat přesné řešení pohybu
těžkého setrvačníku, je podán v [14]. Nejčastěji je uvažován pohyb těžkého symetric-kého
setrvačníku, jehož pevný bod leží na ose symetrie setrvačníku. Přesné řešení
problému lze nalézt v [11], [12], [14]; zde se omezíme na přibližné řešení.
V čl. 6.4 jsme zavedli název těžký
setrvačník pro těleso otáčející se v tíhovém poli kolem bodu, který není
hmotným středem tělesa. Přehled případů, kdy lze podat přesné řešení pohybu
těžkého setrvačníku, je podán v [14]. Nejčastěji je uvažován pohyb těžkého symetric-kého
setrvačníku, jehož pevný bod leží na ose symetrie setrvačníku. Přesné řešení
problému lze nalézt v [11], [12], [14]; zde se omezíme na přibližné řešení.
Budeme předpokládat, že se setrvačník velmi rychle otáčí
kolem své osy symetrie. Druhým předpokladem přibližného řešení bude, že moment
setrvačnosti
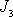 vůči ose symetrie je podstatně větší než druhý hlavní moment
vůči ose symetrie je podstatně větší než druhý hlavní moment
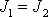 setrvač-níku. V minulém článku jsme
ukázali, že osa otáčení volného setrvačníku, který se otáčí kolem některé ze
svých hlavních os setrvačnosti, zachovává v tělese i v prostoru svou
polohu. Dále jsme ukázali (viz rovnici
(6,96)
), že pro symetrický setrvačník za
předpokladu
setrvač-níku. V minulém článku jsme
ukázali, že osa otáčení volného setrvačníku, který se otáčí kolem některé ze
svých hlavních os setrvačnosti, zachovává v tělese i v prostoru svou
polohu. Dále jsme ukázali (viz rovnici
(6,96)
), že pro symetrický setrvačník za
předpokladu
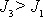 je rotace kolem osy symetrie setrvačníku
energeticky stabilní. Při rychlém otáčení je stabilita natolik velká, že
v dobrém přiblížení lze pokládat osu symetrie setrvačníku za osu otáčení
v tělese pevnou, i když na setrvačník působí nepříliš velký moment
vnějších sil.
je rotace kolem osy symetrie setrvačníku
energeticky stabilní. Při rychlém otáčení je stabilita natolik velká, že
v dobrém přiblížení lze pokládat osu symetrie setrvačníku za osu otáčení
v tělese pevnou, i když na setrvačník působí nepříliš velký moment
vnějších sil.
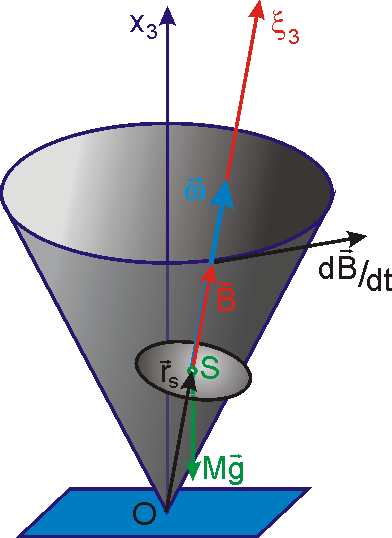
Na obr.76 je znázorněn těžký symetrický setrvačník
s podepřeným bodem na ose symetrie setrvačníku. Pro rychle se otáčející
setrvačník můžeme moment tíhových sil působící na těleso pokládat za nepříliš
velký moment vnějších sil. Potom dle učiněných předpokladů moment hybnosti
 a úhlová rychlost otáčení
a úhlová rychlost otáčení
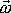 mají směr osy symetrie setrvačníku, kterou
jako třetí osu soustavy souřadnic spjaté se setrvačníkem značíme
mají směr osy symetrie setrvačníku, kterou
jako třetí osu soustavy souřadnic spjaté se setrvačníkem značíme
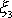 . Dle druhé věty impulsové
(5,49)
je
. Dle druhé věty impulsové
(5,49)
je
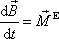 . . |
(5,49) |
Jak jsme ukázali v čl. 5.7, silové působení na těleso
v tíhovém poli lze vystihnout tíhou
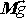 tělesa umístěnou v jeho hmotném středu
S. Výsledný moment vnějších sil působících na těleso je tedy
tělesa umístěnou v jeho hmotném středu
S. Výsledný moment vnějších sil působících na těleso je tedy
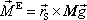 . . |
(6,98) |
V rovnici
(6,98)
je
 označen polohový vektor
označen polohový vektor
 hmotného středu setrvačníku. Počátek
soustavy souřadné pevné v prostoru i soustavy souřadné pevné v tělese
pokládáme do pevného bodu setrvačníku O. Dosadíme-li za
hmotného středu setrvačníku. Počátek
soustavy souřadné pevné v prostoru i soustavy souřadné pevné v tělese
pokládáme do pevného bodu setrvačníku O. Dosadíme-li za
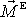 ze
(6,98)
do
(5,49)
, dostáváme
ze
(6,98)
do
(5,49)
, dostáváme
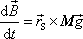 . . |
(6,99) |
Dle rovnice
(6,99)
je
 kolmé k
kolmé k
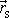 a k
a k
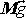 . Uvážíme-li, že
. Uvážíme-li, že
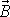 je rovnoběžné s
je rovnoběžné s
 , je jeho časová změna
, je jeho časová změna
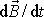 kolmá též k celkovému momentu
hybnosti
kolmá též k celkovému momentu
hybnosti
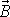 setrvačníku. Jak jsme již uvažovali
v rovnici
(6,91)
i zde časová změna
setrvačníku. Jak jsme již uvažovali
v rovnici
(6,91)
i zde časová změna
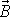 je kolmá k
je kolmá k
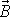 , a tedy velikost B momentu hybnosti zůstává
zachována, s časem se mění pouze směr vektoru
, a tedy velikost B momentu hybnosti zůstává
zachována, s časem se mění pouze směr vektoru
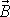 . Má-li
. Má-li
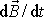 být kolmé k
být kolmé k
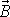 a také k
a také k
 , musí se
, musí se
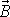 pohybovat po plášti kužele naznačeného na
obr.76. Vzájemný vztah vektoru
pohybovat po plášti kužele naznačeného na
obr.76. Vzájemný vztah vektoru
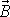 a
a
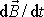 je stejného druhu jako vzájemný vztah vektoru
je stejného druhu jako vzájemný vztah vektoru
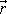 a
a
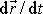 při otáčení hmotného bodu kolem osy. Při
otáčení kolem osy jsme vztah vektoru rychlosti
při otáčení hmotného bodu kolem osy. Při
otáčení kolem osy jsme vztah vektoru rychlosti
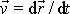 a polohového vektoru
a polohového vektoru
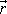 hmotného bodu vyjádřili dle
(5,13)
(viz též
obr.40) jako
hmotného bodu vyjádřili dle
(5,13)
(viz též
obr.40) jako
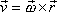 . . |
(5,13) |
V rovnici
(5,13)
je
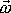 vektor úhlové rychlosti otáčení hmotného
bodu, tj. vektor ve směru osy, kolem které se hmotný bod otáčí (pozor na
formální shodu s označením
vektor úhlové rychlosti otáčení hmotného
bodu, tj. vektor ve směru osy, kolem které se hmotný bod otáčí (pozor na
formální shodu s označením
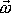 vektoru okamžité rychlosti otáčení
setrvačníku). Analogicky k rovnici
(5,13)
můžeme pro rychlost změny
vektoru okamžité rychlosti otáčení
setrvačníku). Analogicky k rovnici
(5,13)
můžeme pro rychlost změny
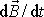 vektoru
vektoru
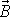 psát vyjádření
psát vyjádření
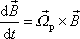 , , |
(6,100) |
 kde
kde
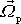 je vektor ve směru svislé osy
je vektor ve směru svislé osy
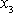 naznačené na obr.76. Velikost
naznačené na obr.76. Velikost
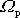 vektoru
vektoru
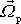 je rovna úhlové rychlosti otáčení koncového
bodu vektoru
je rovna úhlové rychlosti otáčení koncového
bodu vektoru
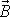 , a tedy i celého vektoru
, a tedy i celého vektoru
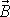 vůči ose
vůči ose
 . Porovnáním rovnic
(6,99)
a
(6,100)
dostáváme
. Porovnáním rovnic
(6,99)
a
(6,100)
dostáváme
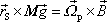 . . |
(6,101) |
Vektory
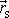 a
a
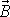 jsou souhlasně a vektory
jsou souhlasně a vektory
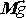 a
a
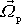 nesouhlasně rovnoběžné (viz obr.77).
Rovnají-li se vektory na obou stranách rovnice
(6,101)
, rovnají se i jejich
velikosti, tedy
nesouhlasně rovnoběžné (viz obr.77).
Rovnají-li se vektory na obou stranách rovnice
(6,101)
, rovnají se i jejich
velikosti, tedy
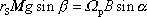 . . |
Uvědomíme-li si (viz obr.77), že
 , potom
, potom
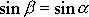 a z poslední rovnice plyne vyjádření
pro velikost
a z poslední rovnice plyne vyjádření
pro velikost
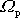 vektoru
vektoru
 ,
,
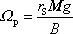 . . |
(6,102) |
Vektor
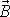 se otáčí kolem svislé osy
se otáčí kolem svislé osy
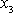 úhlovou rychlostí
úhlovou rychlostí
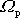 danou rovnicí
(6,102)
. Dle předpokladu o
stabilitě rotace je vektor
danou rovnicí
(6,102)
. Dle předpokladu o
stabilitě rotace je vektor
 rovnoběžný s osou symetrie
rovnoběžný s osou symetrie
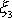 setrvačníku. V uvažovaném přiblížení
můžeme nyní popsat pohyb těžkého symetrického setrvačníku, jehož
v prostoru pevný bod O leží na ose symetrie setrvačníku:
setrvačníku. V uvažovaném přiblížení
můžeme nyní popsat pohyb těžkého symetrického setrvačníku, jehož
v prostoru pevný bod O leží na ose symetrie setrvačníku:
Osa symetrie setrvačníku se otáčí
kolem svislé přímky proložené pevným bodem setrvačníku úhlovou rychlostí
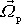 o velikosti
o velikosti
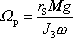 . . |
(6,103) |
Úhlovou rychlost
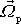 nazýváme precesní rychlostí. Jednotlivé
polohy osy symetrie setrvačníku vytvářejí plášť kužele s vrcholem
v pevném bodě setrvačníku a svislou osou (viz obr.76). V rovnici
(6,103)
je
nazýváme precesní rychlostí. Jednotlivé
polohy osy symetrie setrvačníku vytvářejí plášť kužele s vrcholem
v pevném bodě setrvačníku a svislou osou (viz obr.76). V rovnici
(6,103)
je
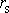 vzdálenost hmotného středu setrvačníku od
pevného bodu O, M
hmotnost setrvačníku, g
velikost tíhového zrychlení,
vzdálenost hmotného středu setrvačníku od
pevného bodu O, M
hmotnost setrvačníku, g
velikost tíhového zrychlení,
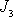 moment setrvačnosti vůči ose symetrie
setrvačníku a
moment setrvačnosti vůči ose symetrie
setrvačníku a
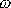 velikost úhlové rychlosti otáčení
setrvačníku kolem jeho osy symetrie.
velikost úhlové rychlosti otáčení
setrvačníku kolem jeho osy symetrie.
V rovnici
(6,103)
jsme B z rovnice
(6,102)
nahradili
výrazem
 , neboť předpokládáme, že
, neboť předpokládáme, že
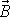 je rovnoběžné s
je rovnoběžné s
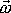 a má směr osy
a má směr osy
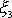 .
.
Rovnice
(6,103)
udává rychlost
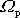 precese těžkého setrvačníku v prostoru.
Vidíme, že pro daný setrvačník a způsob upevnění je precesní rychlost nepřímo
úměrná rychlosti
precese těžkého setrvačníku v prostoru.
Vidíme, že pro daný setrvačník a způsob upevnění je precesní rychlost nepřímo
úměrná rychlosti
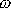 otáčení setrvačníku kolem své osy. Začne-li
se setrvačník brzdit,
otáčení setrvačníku kolem své osy. Začne-li
se setrvačník brzdit,
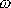 klesá a rychlost precese
klesá a rychlost precese
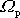 stoupá. Při větším zbrzdění nemůžeme již
pokládat osu otáčení setrvačníku za osu pevnou v tělese, předpoklady
učiněné při právě provedeném odvození precesního pohybu přestanou platit,
setrvačník se začne pohybovat složitějším pohybem, při kterém jeho osa začne
periodicky měnit svou výšku v tíhovém poli a nakonec setrvačník spadne.
stoupá. Při větším zbrzdění nemůžeme již
pokládat osu otáčení setrvačníku za osu pevnou v tělese, předpoklady
učiněné při právě provedeném odvození precesního pohybu přestanou platit,
setrvačník se začne pohybovat složitějším pohybem, při kterém jeho osa začne
periodicky měnit svou výšku v tíhovém poli a nakonec setrvačník spadne.
Naznačíme, jak se liší přesné
řešení pohybu těžkého symetrického setrvačníku od výše uvažovaného přibližného
řešení. Ve stati 6.5.3 při rozboru stability rotace jsme ukázali, že působením
momentu síly na osu otáčení setrvačníku se poloha osy otáčení
v setrvačníku změní. Začne-li na symetrický setrvačník roztočený kolem své
osy symetrie působit moment síly, např. moment
(6,98)
tíhy setrvačníku
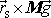 , osa otáčení přestane mít směr osy symetrie setrvačníku. Směr osy symetrie
setrvačníku
, osa otáčení přestane mít směr osy symetrie setrvačníku. Směr osy symetrie
setrvačníku
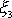 se odchýlí od směru momentu hybnosti
se odchýlí od směru momentu hybnosti
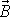 a od směru vektoru okamžité úhlové rychlosti
otáčení
a od směru vektoru okamžité úhlové rychlosti
otáčení
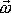 setrvačníku. Osa symetrie setrvačníku se
začne otáčet kolem směru momentu hybnosti
setrvačníku. Osa symetrie setrvačníku se
začne otáčet kolem směru momentu hybnosti
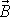 způsobem popsaným v minulém článku při výkladu
regulární precese volného setrvačníku. Precesní pohyb osy
způsobem popsaným v minulém článku při výkladu
regulární precese volného setrvačníku. Precesní pohyb osy
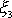 kolem směru
kolem směru
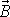 bývá označován jako nutace
osy setrvačníku. Celkový pohyb osy symetrie setrvačníku
vznikne spojením nutace kolem směru
bývá označován jako nutace
osy setrvačníku. Celkový pohyb osy symetrie setrvačníku
vznikne spojením nutace kolem směru
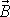 a precese momentu hybnosti
a precese momentu hybnosti
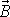 po kuželi naznačeném na obr.76. Myslíme-li
si na ose setrvačníku bod různý od pevného bodu setrvačníku, kreslí tento bod
na kulové ploše křivku analogickou cykloidě (viz obrázky v [11], [12], [14]).
Pohyb těžkého setrvačníku, který se nutací osy setrvačníku liší od čisté
precese, se nazývá pseudoregulární precese.
po kuželi naznačeném na obr.76. Myslíme-li
si na ose setrvačníku bod různý od pevného bodu setrvačníku, kreslí tento bod
na kulové ploše křivku analogickou cykloidě (viz obrázky v [11], [12], [14]).
Pohyb těžkého setrvačníku, který se nutací osy setrvačníku liší od čisté
precese, se nazývá pseudoregulární precese.
Za předpokladů učiněných na začátku tohoto článku
rychlá rotace a setrvačník odpovídající hovorovému pojmu setrvačník (
 ) je odchýlení osy otáčení setrvačníku od
osy symetrie setrvačníku způsobené momentem tíhových sil malé. Nutaci osy
setrvačníku lze pak zanedbat, pohyb těžkého symetrického můžeme pokládat za
čistou precesi. Za míru pro posouzení, jak velkou odchylku od čisté precese
způsobí moment tíhových sil
(6,98)
) je odchýlení osy otáčení setrvačníku od
osy symetrie setrvačníku způsobené momentem tíhových sil malé. Nutaci osy
setrvačníku lze pak zanedbat, pohyb těžkého symetrického můžeme pokládat za
čistou precesi. Za míru pro posouzení, jak velkou odchylku od čisté precese
způsobí moment tíhových sil
(6,98)
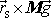 ,
,
může přibližně sloužit poměr kinetické energie
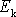 setrvačníku a potenciální energie
setrvačníku a potenciální energie
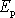 setrvačníku v tíhovém poli.
setrvačníku v tíhovém poli.
 Položíme-li nulovou hladinu potenciální energie do pevného bodu O setrvačníku, je dle
obr.77 potenciální energie setrvačníku
Položíme-li nulovou hladinu potenciální energie do pevného bodu O setrvačníku, je dle
obr.77 potenciální energie setrvačníku
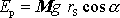 . Kinetickou energii setrvačníku lze v dobrém přiblížení (viz
(6,68)
)
vyjádřit jako
. Kinetickou energii setrvačníku lze v dobrém přiblížení (viz
(6,68)
)
vyjádřit jako
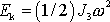 . Mějme setrvačník válcového tvaru, jehož rozměry jsou znázorněny na obr.78 a
který má hmotnost
. Mějme setrvačník válcového tvaru, jehož rozměry jsou znázorněny na obr.78 a
který má hmotnost
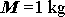 . Moment setrvačnosti vůči ose symetrie
. Moment setrvačnosti vůči ose symetrie
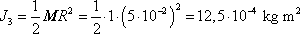 . . |
Předpokládáme-li, že velikost úhlové rychlosti otáčení
setrvačníku
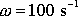 , je kinetická energie setrvačníku
, je kinetická energie setrvačníku
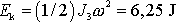 . Uvažujeme-li největší hodnotu potenciální energie setrvačníku, tedy případ,
kdy
. Uvažujeme-li největší hodnotu potenciální energie setrvačníku, tedy případ,
kdy
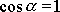 , dostaneme
, dostaneme
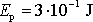 . Kinetická energie
. Kinetická energie
 i při ne příliš rychlé rotaci je podstatně
větší než potenciální energie
i při ne příliš rychlé rotaci je podstatně
větší než potenciální energie
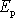 .
.
Poměr kinetické energie
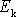 a potenciální energie
a potenciální energie
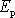 určuje též poměr precesní rychlosti
určuje též poměr precesní rychlosti
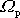 těžkého setrvačníku a jeho rychlosti vlastní rotace
těžkého setrvačníku a jeho rychlosti vlastní rotace
 . Vydělíme-li rovnici
(6,103)
hodnotou
. Vydělíme-li rovnici
(6,103)
hodnotou
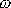 , dostáváme
, dostáváme
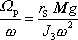 . . |
(6,104) |
V čitateli na pravé straně rovnice
(6,104)
je hodnota,
kterou jsme brali jako míru potenciální energie setrvačníku a ve jmenovateli je
dvojnásobná hodnota kinetické energie setrvačníku. Kinetická energie
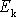 musí být podstatně vyšší než potenciální energie
musí být podstatně vyšší než potenciální energie
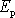 , abychom pohyb těžkého symetrického setrvačníku mohli pokládat za čistou
precesi. Z rovnice
(6,104)
plyne, že pro
, abychom pohyb těžkého symetrického setrvačníku mohli pokládat za čistou
precesi. Z rovnice
(6,104)
plyne, že pro
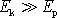 je
je
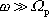 . . |
(6,105) |
Precese těžkého symetrického setrvačníku, pro který
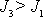 , je přibližné vyjádření pohybu, který setrvačník koná, je-li rychle roztočen
kolem své osy symetrie
, je přibližné vyjádření pohybu, který setrvačník koná, je-li rychle roztočen
kolem své osy symetrie
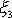 . Přitom dle
(6,105)
je rychlost w vlastní
rotace setrvačníku podstatně větší než precesní rychlost
. Přitom dle
(6,105)
je rychlost w vlastní
rotace setrvačníku podstatně větší než precesní rychlost
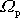 . Regulární precese volného symetrického setrvačníku popsaná v minulém
článku je pohybem, který volný symetrický setrvačník koná, je-li roztočen
libovolnou úhlovou rychlostí kolem některé své osy, která není hlavní
osou setrvačnosti. Přitom žádná nerovnost typu
(6,105)
neplatí, úhlová rychlost
rotace kolem osy symetrie volného setrvačníku často bývá i menší než precesní
úhlová rychlost
. Regulární precese volného symetrického setrvačníku popsaná v minulém
článku je pohybem, který volný symetrický setrvačník koná, je-li roztočen
libovolnou úhlovou rychlostí kolem některé své osy, která není hlavní
osou setrvačnosti. Přitom žádná nerovnost typu
(6,105)
neplatí, úhlová rychlost
rotace kolem osy symetrie volného setrvačníku často bývá i menší než precesní
úhlová rychlost
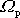 , jak plyne z rovnice
(6,89)
.
, jak plyne z rovnice
(6,89)
.
Zdůrazníme charakteristický rys
pohybu setrvačníků, o kterém jsme se již zmínili při vyšetřování stability
rotace kolem hlavních os (viz obr.75) a při rozboru rovnice
(6,99)
. Mějme
symetrický setrvačník, jehož moment setrvačnosti
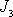 vůči ose symetrie je větší než druhý hlavní
moment setrvačnosti
vůči ose symetrie je větší než druhý hlavní
moment setrvačnosti
 , tedy hovorový setrvačník . Roztočíme jej rychle kolem osy symetrie a začneme
na něj působit dvojicí sil
, tedy hovorový setrvačník . Roztočíme jej rychle kolem osy symetrie a začneme
na něj působit dvojicí sil
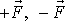 , které jsou kolmé k ose symetrie setrvačníku. Moment
, které jsou kolmé k ose symetrie setrvačníku. Moment
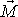 sil
sil
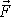 je kolmý ke směru sil
je kolmý ke směru sil
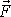 . Dle rovnice
(5,49)
. Dle rovnice
(5,49)
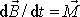 a tedy změna celkového momentu hybnosti
a tedy změna celkového momentu hybnosti
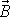 je kolmá ke směru působících sil. Jelikož
předpokládáme stabilitu rotace kolem osy symetrie setrvačníku, zůstávají i při
působení sil
je kolmá ke směru působících sil. Jelikož
předpokládáme stabilitu rotace kolem osy symetrie setrvačníku, zůstávají i při
působení sil
 vektor
vektor
 , vektor úhlové rychlosti otáčení setrvačníku
, vektor úhlové rychlosti otáčení setrvačníku
 a směr osy symetrie setrvačníku rovnoběžné.
Kolmá ke směru sil
a směr osy symetrie setrvačníku rovnoběžné.
Kolmá ke směru sil
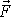 je tedy nejen změna
je tedy nejen změna
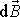 vektoru
vektoru
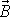 , ale i změna
, ale i změna
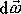 vektoru
vektoru
 a změna směru osy symetrie setrvačníku v prostoru.
a změna směru osy symetrie setrvačníku v prostoru.
 Pohyb setrvačníku vyvolaný dvojicí sil
Pohyb setrvačníku vyvolaný dvojicí sil
 ,
,
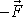 je znázorněn na obr.79. Písmenem o
je označena osa, kolem které se osa symetrie
setrvačníku začne otáčet, symbolem
je znázorněn na obr.79. Písmenem o
je označena osa, kolem které se osa symetrie
setrvačníku začne otáčet, symbolem
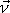 je znázor-něn jednotkový vektor ve směru osy
symetrie setrvačníku. Uvedené skutečnosti jsou zákla-dem podivného chování
setrvačníků. Zač-neme-li převracet setrvačník, např. rychle se otáčející
kolo, které držíme za jeho osu (mezi osou a kolem jsou ložiska), necítíme odpor
proti směru našeho silového působení, ale osa kola se nám snaží vyklouznout kolmo
na směr, ve kterém na ni rukama působíme.
je znázor-něn jednotkový vektor ve směru osy
symetrie setrvačníku. Uvedené skutečnosti jsou zákla-dem podivného chování
setrvačníků. Zač-neme-li převracet setrvačník, např. rychle se otáčející
kolo, které držíme za jeho osu (mezi osou a kolem jsou ložiska), necítíme odpor
proti směru našeho silového působení, ale osa kola se nám snaží vyklouznout kolmo
na směr, ve kterém na ni rukama působíme.
Uvažovaný efekt, říká se mu gyroskopický ( setrvačník v technických oborech bývá nazýván gyroskopem), je třeba brát v úvahu při konstrukcích strojů, v kterých jsou velké, rychle se otáčející součásti. Když je např. v letadle uložena rychle rotující součást s velkým momentem setrvačnosti s osou rotace ve směru podélné osy letadla, dochází při zatáčení letadla k zvedání nebo klesání jeho špičky podle vzájemného poměru smyslu rotace a směru zatáčky. Obdobné problémy mohou nastat i při konstrukci lodí a automobilů.
Na gyroskopickém efektu je založen i přístroj zvaný gyrokompas, kterým bývá nahrazován klasický magnetický kompas, a jemu příbuzný gyroteodolit. U těchto přístrojů gyroskopický efekt na setrvačník s velkým momentem hybnosti (velmi rychle se otáčející) vyvolá rotace Země. Slabý moment sil, kterým Země působí vůči inerciální soustavě na osu setrvačníku, stačí vyvolat gyroskopický efekt, který se projevuje snahou ztotožnit osu rotujícího setrvačníku se severojižním směrem. Gyrokompasy a gyroteodolity lze zkonstruovat tak, že jejich přesnost v určení absolutního směru na Zemi vysoce předčí klasické kompasy a buzoly.
Stabilita rotace setrvačníku kolem jeho osy symetrie bývá
technicky využívána. Rychle roztočený setrvačník poháněný elektromotorem slouží
jako přístroj zvaný umělý horizont k určení polohy letadla při létání za
ztížené viditelnosti. Stabilita rotujících kol, ale též výše zmíněný
gyroskopický efekt, umožňují jízdu na kole a na motocyklu. Střely se roztáčejí
v hlavních zbraní, aby po dobu letu lépe zachovávaly směr své osy
v prostoru. Do osobních námořních lodí se montují velké setrvačníky, aby
udržovaly polohu lodí při vlnobití a chránily cestující před mořskou nemocí.
Některé další aplikace setrvačníků spolu s podrobnějším výkladem jejich
činnosti lze nalézt např. v
 .
.