Eulerovy rovnice
(6,43)
mají pro pohyb volného
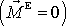 setrvačníku tvar
setrvačníku tvar
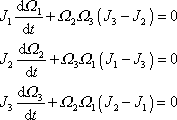 . . |
(6,71) |
Máme-li kulový setrvačník, je
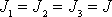 a rovnice
(6,71)
se redukují na tvar
a rovnice
(6,71)
se redukují na tvar
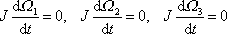 . . |
(6,72) |
Z rovnice
(6,72)
plyne, že všechny složky
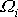 vektoru úhlové rychlosti otáčení jsou
s časem konstantní. Osa otáčení volného kulového setrvačníku má
v tělese, tj. v setrvačníku, stálou polohu a setrvačník kolem ní
rotuje se stálou velikostí úhlové rychlosti. Moment hybnosti
vektoru úhlové rychlosti otáčení jsou
s časem konstantní. Osa otáčení volného kulového setrvačníku má
v tělese, tj. v setrvačníku, stálou polohu a setrvačník kolem ní
rotuje se stálou velikostí úhlové rychlosti. Moment hybnosti
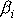 je dle
(6,37)
je dle
(6,37)
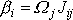 . Pro kulový setrvačník je
. Pro kulový setrvačník je
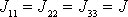 a ostatní složky tensoru setrvačnosti
a ostatní složky tensoru setrvačnosti
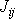 jsou nulové, tedy
jsou nulové, tedy
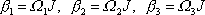 . . |
(6,73) |
Z rovnic
(6,73)
plyne, že moment hybnosti
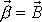 je skalárním násobkem vektoru úhlové
rychlosti otáčení
je skalárním násobkem vektoru úhlové
rychlosti otáčení
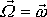 ,
,
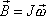 . . |
(6,74) |
Rovnici (6,74) jsme odvodili v soustavě souřadné spjaté s tělesem. Jelikož je to rovnice mezi vektory, je její obsah nezávislý na volbě soustavy souřadné, platí tedy i v soustavě souřadné pevné v prostoru.
Z druhé věty impulsové
(5,49)
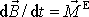 pro volný setrvačník plyne
pro volný setrvačník plyne
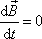 , , |
(6,75) |
neboť výsledný moment vnějších sil
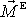 působící na volný setrvačník je nulový,
působící na volný setrvačník je nulový,
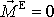 . Dle rovnice
(6,75)
je moment hybnosti
. Dle rovnice
(6,75)
je moment hybnosti
 volného setrvačníku v prostoru
s časem konstantní vektor. Uvážíme-li rovnici
(6,74)
, je také
volného setrvačníku v prostoru
s časem konstantní vektor. Uvážíme-li rovnici
(6,74)
, je také
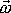 konstantní vektor v prostoru.
konstantní vektor v prostoru.
V kulovém setrvačníku jsou všechny hlavní momenty setrvačnosti, a tedy i momenty setrvačnosti vůči libovolné ose procházející hmotným středem, stejně velké. Z energetického hlediska je tedy rotace kolem libovolné osy indiferentní (volná). I malý náhodný impuls může vést ke změně polohy osy rotace v tělese (srov. stať 6.5.3). Můžeme shrnout:
Volný kulový setrvačník rotuje kolem libovolné osy stálou úhlovou rychlostí, přičemž osa rotace zachovává v prostoru i v tělese po celou dobu pohybu stálou polohu. Poloha osy rotace v tělese však není stabilní.
Vyšetříme nyní pohyb volného symetrického setrvačníku. Budeme předpokládat, že osa
rotační symetrie setrvačníku je třetí osa, potom mezi hlavními momenty
setrvačnosti platí relace
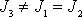 . Pohybové rovnice
(6,71)
volných setrvačníků se pro symetrický setrvačník,
označíme-li stejné hodnoty hlavních momentů setrvačnosti vůči osám kolmým
k ose symetrie
. Pohybové rovnice
(6,71)
volných setrvačníků se pro symetrický setrvačník,
označíme-li stejné hodnoty hlavních momentů setrvačnosti vůči osám kolmým
k ose symetrie
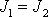 symbolem
symbolem
 , zjednoduší na tvar
, zjednoduší na tvar
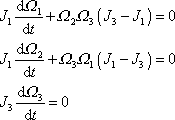 . . |
(6,76) |
Z poslední rovnice systému (6,76) plyne
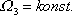 . . |
(6,77) |
Časovou závislost druhých dvou složek
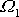 a
a
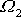 vektoru
vektoru
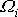 získáme řešením soustavy prvých dvou
diferenciálních rovnic
(6,76)
, které snadno přepíšeme na tvar
získáme řešením soustavy prvých dvou
diferenciálních rovnic
(6,76)
, které snadno přepíšeme na tvar
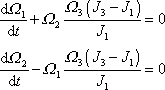 . . |
(6,78) |
Výraz
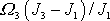 je, přihlédneme-li k
(6,77)
, konstantní a má
rozměr úhlové rychlosti. Označíme jej
je, přihlédneme-li k
(6,77)
, konstantní a má
rozměr úhlové rychlosti. Označíme jej
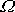 . Z prvé rovnice
(6,78)
vypočteme
. Z prvé rovnice
(6,78)
vypočteme
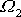 ,
,
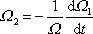 |
a derivováním poslední rovnice dostaneme
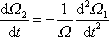 . . |
Získané vyjádření
 dosadíme do druhé z rovnic
(6,78)
a
dostaneme diferenciální rovnici pro hledanou funkci
dosadíme do druhé z rovnic
(6,78)
a
dostaneme diferenciální rovnici pro hledanou funkci
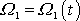 ,
,
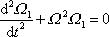 . . |
(6,79) |
Rovnice
(6,79)
je pro určení funkce
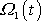 diferenciální rovnicí stejného tvaru jako
rovnice harmonického kmitu
(2,10)
pro určení funkce
diferenciální rovnicí stejného tvaru jako
rovnice harmonického kmitu
(2,10)
pro určení funkce
 . Analogicky s řešením rovnice
(2,10)
je řešením rovnice
(6,79)
. Analogicky s řešením rovnice
(2,10)
je řešením rovnice
(6,79)
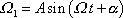 . . |
(6,80) |
Dosadíme-li řešení (6,80) do prvé z rovnic (6,78) , dostáváme
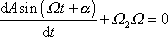 , , |
odkud
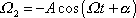 . . |
(6,81) |
Konstanty A a
 lze určit z počátečních podmínek pohybu, obvykle udáním vektoru úhlové rychlosti otáčení
lze určit z počátečních podmínek pohybu, obvykle udáním vektoru úhlové rychlosti otáčení
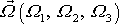 v čase
v čase
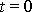 , tj. udáním směru osy, vůči které těleso roztočíme a hodnoty (velikost a smysl)
úhlové rychlosti otáčení.
, tj. udáním směru osy, vůči které těleso roztočíme a hodnoty (velikost a smysl)
úhlové rychlosti otáčení.
 Rozebereme nejprve obecný případ získaného řešení, kdy všechny tři složky vektoru
Rozebereme nejprve obecný případ získaného řešení, kdy všechny tři složky vektoru
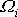 jsou nenulové. Položíme-li počátek vektoru
jsou nenulové. Položíme-li počátek vektoru
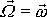 do počátku soustavy souřadnic, tj. do
hmotného středu setrvačníku, lze rovnice
(6,77)
,
(6,80)
a
(6,81)
pokládat za
parametrické rovnice trajektorie koncového bodu vektoru
do počátku soustavy souřadnic, tj. do
hmotného středu setrvačníku, lze rovnice
(6,77)
,
(6,80)
a
(6,81)
pokládat za
parametrické rovnice trajektorie koncového bodu vektoru
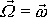 v sou-řadnicové soustavě spjaté
s tělesem. Uvažujeme-li ve fyzikálním rozměru úhlové rychlosti, jsou
rovnice
(6,77)
,
(6,80)
a
(6,81)
parametrickými rovnicemi kružnice o poloměru A
(rozměr
v sou-řadnicové soustavě spjaté
s tělesem. Uvažujeme-li ve fyzikálním rozměru úhlové rychlosti, jsou
rovnice
(6,77)
,
(6,80)
a
(6,81)
parametrickými rovnicemi kružnice o poloměru A
(rozměr
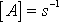 ), jež má střed na ose
), jež má střed na ose
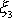 a která leží v rovině
a která leží v rovině
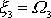 , tj. v rovině kolmé k ose
, tj. v rovině kolmé k ose
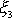 vzdálené
vzdálené
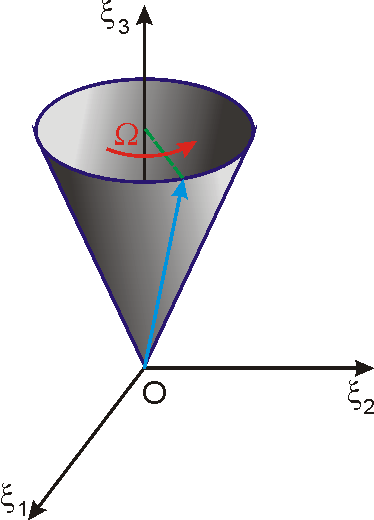
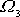 od počátku souřadnicové soustavy. Vektor
úhlové rychlosti
od počátku souřadnicové soustavy. Vektor
úhlové rychlosti
 opisuje tedy v tělese plášť kužele
znázor-něného na obr.70. Kužel, který opisuje vektor
opisuje tedy v tělese plášť kužele
znázor-něného na obr.70. Kužel, který opisuje vektor
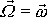 v tělese, se nazývá polodiový kužel.
v tělese, se nazývá polodiový kužel.
Koncový bod vektoru
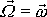 se otáčí kolem osy
se otáčí kolem osy
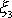 úhlovou rychlostí
úhlovou rychlostí
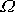 , jak plyne z rovnic
(6,80)
a
(6,81)
. Úhlová rychlost
, jak plyne z rovnic
(6,80)
a
(6,81)
. Úhlová rychlost
 byla zavedena v textu k rovnici
(6,78)
jako
byla zavedena v textu k rovnici
(6,78)
jako
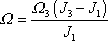 |
(6,82) |
a udává rychlost otáčení neboli, jak říkáme, precesi vektoru
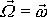 po polodiovém kuželi. Úhlovou rychlost
po polodiovém kuželi. Úhlovou rychlost
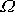 nazýváme rychlostí precese osy otáčení v tělese.
Z provedeného rozboru pohybu vektoru
nazýváme rychlostí precese osy otáčení v tělese.
Z provedeného rozboru pohybu vektoru
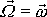 v tělese plyne, že jeho velikost
v tělese plyne, že jeho velikost
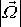 je též s časem konstantní.
je též s časem konstantní.
Známe-li tensor momentu setrvačnosti tělesa a vektor úhlové rychlosti
 , můžeme dle
(6,37)
stanovit složky
, můžeme dle
(6,37)
stanovit složky
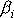 vektoru celkového momentu hybnosti
vektoru celkového momentu hybnosti
 v soustavě souřadnic spjaté
s tělesem. Vzhledem k volbě souřadnicové soustavy ve směru hlavních
os setrvačnosti, mají rovnice
(6,37)
v soustavě souřadnic spjaté
s tělesem. Vzhledem k volbě souřadnicové soustavy ve směru hlavních
os setrvačnosti, mají rovnice
(6,37)
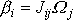 jednoduchý tvar
jednoduchý tvar
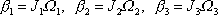 . . |
(6,83) |
Jelikož setrvačník je symetrický (
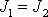 ), rovnice
(6,83)
se dále zjednoduší,
), rovnice
(6,83)
se dále zjednoduší,
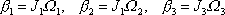 , , |
Z poslední rovnice plyne, že poměr
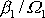 je stejný jako poměr
je stejný jako poměr
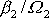 . Geometricky to znamená, že vektory
. Geometricky to znamená, že vektory
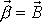 a
a
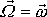 , položíme-li jejich počátky do počátku souřadnicové soustavy, leží v jedné
rovině s osou
, položíme-li jejich počátky do počátku souřadnicové soustavy, leží v jedné
rovině s osou
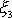 . Na obr.71 jsou naznačeny polohy vektorů
. Na obr.71 jsou naznačeny polohy vektorů
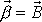 a
a
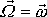 ve zmíněné rovině. Konstantní výraz
ve zmíněné rovině. Konstantní výraz
 je ve shodě s
(6,80)
a
(6,81)
označen A.
Poměr tangent úhlů
je ve shodě s
(6,80)
a
(6,81)
označen A.
Poměr tangent úhlů
Úhel b nesmí být zaměňován s velikostí vektoru celkového momentu hybnosti, pro který by se mohl užívat stejný symbol.
 a
a
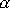 je dán poměrem momentů setrvačnosti
je dán poměrem momentů setrvačnosti
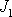 a
a
 ,
,
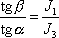 . . |
(6,84) |
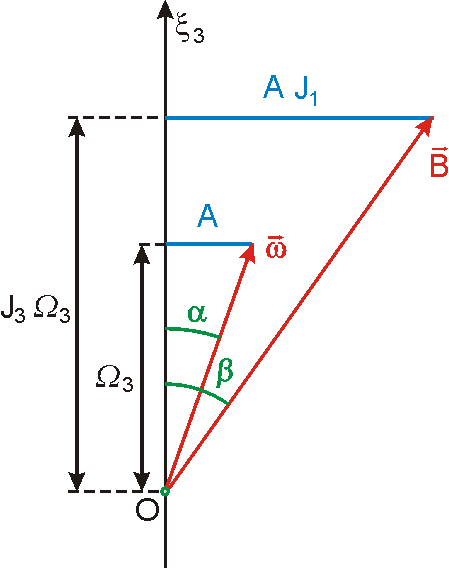 Na obr.71 je nakreslen případ, kdy
Na obr.71 je nakreslen případ, kdy
 . Je-li
. Je-li
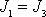 , je setrvačník kulový a vektory momentu hybnosti a úhlové rychlosti otáčení leží
v jedné přímce, a jsou tedy rovnoběžné,
, je setrvačník kulový a vektory momentu hybnosti a úhlové rychlosti otáčení leží
v jedné přímce, a jsou tedy rovnoběžné,
 . Pro
. Pro
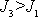 , leží vektor
, leží vektor
 blíže k ose než vektor
blíže k ose než vektor
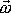 .
.
Vektor
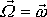 se otáčí kolem osy
se otáčí kolem osy
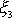 úhlovou rychlostí
úhlovou rychlostí
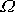 . Mají-li vektory
. Mají-li vektory
 a
a
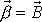 stále ležet v jedné rovině, musí se vektor
stále ležet v jedné rovině, musí se vektor
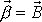 otáčet vůči soustavě souřadnic pevné
v tělese stejnou úhlovou rychlostí
otáčet vůči soustavě souřadnic pevné
v tělese stejnou úhlovou rychlostí
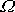 jako vektor
jako vektor
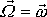 . Vektor
. Vektor
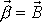 se v tělese také pohybuje po plášti
kužele, který však má obecně jiný vrcholový úhel (viz rovnici
(6,84)
a obr.71)
než polodiový kužel.
se v tělese také pohybuje po plášti
kužele, který však má obecně jiný vrcholový úhel (viz rovnici
(6,84)
a obr.71)
než polodiový kužel.
 Dle rovnice
(6,75)
je vektor momentu hybnosti
Dle rovnice
(6,75)
je vektor momentu hybnosti
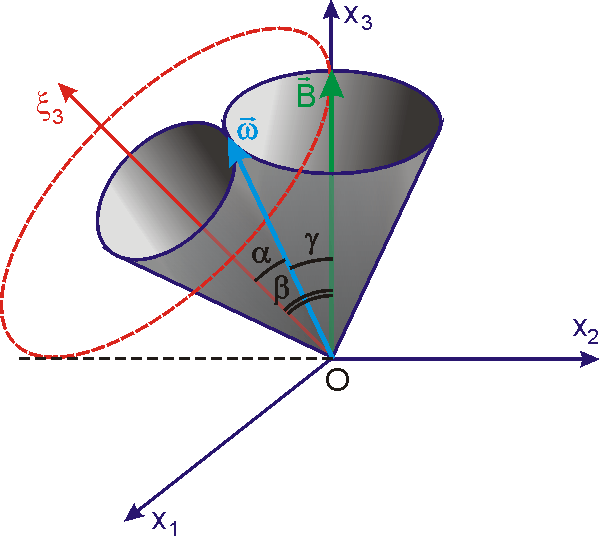
 pevným vektorem v prostoru. Na obr.72
je naznačen moment hybnosti
pevným vektorem v prostoru. Na obr.72
je naznačen moment hybnosti
 jako vektor ve směru osy
jako vektor ve směru osy
 souřadnicové soustavy pevné v prostoru.
Dále je na obrázku naznačen kužel pevný v tělese s vrcholovým
úhlem
souřadnicové soustavy pevné v prostoru.
Dále je na obrázku naznačen kužel pevný v tělese s vrcholovým
úhlem
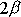 , jehož osou je osa
, jehož osou je osa
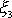 souřadnicové soustavy pevné v tělese.
V plášti tohoto kužele musí dle výše provedených úvah ležet vektor
souřadnicové soustavy pevné v tělese.
V plášti tohoto kužele musí dle výše provedených úvah ležet vektor
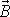 . Zřejmě tedy, jak je vidět i z jednoduššího obr.71, osa
. Zřejmě tedy, jak je vidět i z jednoduššího obr.71, osa
 musí po celou dobu pohybu volného symetrického
setrvač-níku svírat stálý úhel
musí po celou dobu pohybu volného symetrického
setrvač-níku svírat stálý úhel
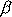 se směrem vektoru
se směrem vektoru
 , který je pevný v prostoru. Jak rychle se osa
, který je pevný v prostoru. Jak rychle se osa
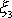 kolem osy
kolem osy
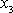 v prosto-ru otáčí, nelze však přímo
z provedené úvahy určit. Víme sice, že vektor
v prosto-ru otáčí, nelze však přímo
z provedené úvahy určit. Víme sice, že vektor
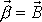 se otáčí kolem osy
se otáčí kolem osy
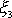 úhlovou rychlostí
úhlovou rychlostí
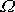 , nevíme však který bod pláště kužele pevného v tělese, kdy splývá s osou
, nevíme však který bod pláště kužele pevného v tělese, kdy splývá s osou
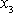 , neboť nevíme, jak vypadá klouzání pláště kužele po ose
, neboť nevíme, jak vypadá klouzání pláště kužele po ose
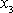 .
.
Na obr.72 jsou naznačeny další dva kužele, polodiový kužel a
kužel, jehož osa prochází v prostoru konstantním vektorem momentu
hybnosti
 a jehož vrcholový úhel
a jehož vrcholový úhel
 . Tento v prostoru pevný kužel se nazývá kužel herpolodiový.
. Tento v prostoru pevný kužel se nazývá kužel herpolodiový.
Dokázali jsme již, že osa
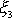 a vektory
a vektory
 a
a
 leží v jedné rovině. Polodiový a
herpolodiový kužel se dotýkají podél přímky, v které leží vektor úhlové
rychlosti otáčení
leží v jedné rovině. Polodiový a
herpolodiový kužel se dotýkají podél přímky, v které leží vektor úhlové
rychlosti otáčení
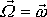 , který je společným vektorem tělesa a prostoru. Dotyková přímka. je okamžitá osa
otáčení setrvačníku. Podél dotykové přímky polodiového a herpolodiového kužele
tudíž nemůže dojít k podklouzávání, polodiový a herpolodiový kužel se po
sobě valí bez klouzání. Velikost rychlosti rotace
, který je společným vektorem tělesa a prostoru. Dotyková přímka. je okamžitá osa
otáčení setrvačníku. Podél dotykové přímky polodiového a herpolodiového kužele
tudíž nemůže dojít k podklouzávání, polodiový a herpolodiový kužel se po
sobě valí bez klouzání. Velikost rychlosti rotace
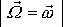 kolem okamžité osy otáčení, tj. rychlost
odvalování, je stálá. Úhly
kolem okamžité osy otáčení, tj. rychlost
odvalování, je stálá. Úhly
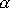 ,
,
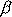 a tím i úhel
a tím i úhel
 lze určit, známe-li momenty
setrvačnosti
lze určit, známe-li momenty
setrvačnosti
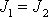 a
a
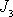 symetrického setrvačníku a počáteční
hodnotu
symetrického setrvačníku a počáteční
hodnotu
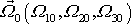 vektoru
vektoru
 .
.
Pohyb volného symetrického setrvačníku lze názorně popsat jako odvalování v tělese pevného polodiového kužele po herpolodiovém kuželi pevném v prostoru.
 Určíme, jak rychle se otáčí osa
Určíme, jak rychle se otáčí osa
 setrvačníku v prostoru. Tato rychlost
se nazývá rychlost precese setrvačníku v prostoru. Označíme ji
setrvačníku v prostoru. Tato rychlost
se nazývá rychlost precese setrvačníku v prostoru. Označíme ji
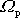 , Dle rovnice
(5,69)
rychlost libovolného bodu tuhého tělesa vůči hmotnému středu
lze určit jako
, Dle rovnice
(5,69)
rychlost libovolného bodu tuhého tělesa vůči hmotnému středu
lze určit jako
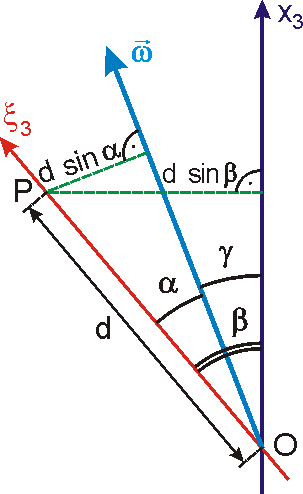
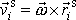 . Bodem tuhého tělesa je i libovolný bod osy setrvačníku, např. bod P znázorněný
na obr.73. Počátek soustavy souřadnic O je zvolen v hmotném středu tělesa.
(Dále budeme u polohového vektoru a u označení rychlosti bodu vynechávat
index S.) Souřadnice
. Bodem tuhého tělesa je i libovolný bod osy setrvačníku, např. bod P znázorněný
na obr.73. Počátek soustavy souřadnic O je zvolen v hmotném středu tělesa.
(Dále budeme u polohového vektoru a u označení rychlosti bodu vynechávat
index S.) Souřadnice
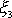 bodu P je označena d.
Velikost rychlosti v bodu P je
bodu P je označena d.
Velikost rychlosti v bodu P je
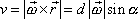 . . |
(6,85) |
Vyjádříme-li rychlost bodu P jako rychlost rotace kolem osy
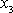 pevné v prostoru, dostáváme pro její velikost
pevné v prostoru, dostáváme pro její velikost
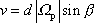 . . |
(6,86) |
Porovnáním rovnic
(6,85)
a
(6,86)
dostáváme poměr velikostí
precesní rychlosti
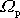 a úhlové rychlosti otáčení
a úhlové rychlosti otáčení
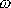 tělesa,
tělesa,
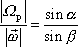 . . |
(6,87) |
Zadáním počáteční hodnoty
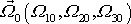 vektoru
vektoru
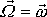 jeho složkami v soustavě souřadné
spjaté s tělesem je dán úhel
jeho složkami v soustavě souřadné
spjaté s tělesem je dán úhel
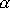 , neboť
, neboť
 , kde
, kde
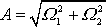 a pomě-rem
(6,84)
je dán i úhel
a pomě-rem
(6,84)
je dán i úhel
 . Rovnicí
(6,87)
je potom určena velikost precesní rychlosti
. Rovnicí
(6,87)
je potom určena velikost precesní rychlosti
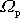 .
.
Pohyb volného symetrického setrvačníku se nazývá regulární precese. Popíšeme, jak probíhá tento pohyb:
Pohyb volného symetrický
symetrického setrvačníku probíhá tak, že osa symetrie setrvačníku svírá
konstantní úhel se směrem v prostoru pevného vektoru celkového momentu
hybnosti
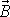 setrvačníku. Osa symetrie setrvačníku se
otáčí kolem osy proložené vektorem
setrvačníku. Osa symetrie setrvačníku se
otáčí kolem osy proložené vektorem
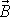 stálou precesní rychlostí
stálou precesní rychlostí
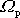 . Setrvačník při tom rotuje kolem své osy symetrie stálou úhlovou rychlostí
. Setrvačník při tom rotuje kolem své osy symetrie stálou úhlovou rychlostí
 , jež je rovna průmětu úhlové rychlosti otáčení setrvačníku
, jež je rovna průmětu úhlové rychlosti otáčení setrvačníku
 do směru osy symetrie setrvačníku. Pro daný
volný symetrický setrvačník, jehož vlastnosti jsou určeny zadáním hlavních
momentů setrvačnosti
do směru osy symetrie setrvačníku. Pro daný
volný symetrický setrvačník, jehož vlastnosti jsou určeny zadáním hlavních
momentů setrvačnosti
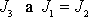 , je konkrétní průběh regulární procese určen počáteční hodnotou
, je konkrétní průběh regulární procese určen počáteční hodnotou
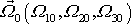 vektoru úhlové rychlosti otáčení
vektoru úhlové rychlosti otáčení
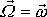 .
.
Velikost
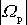 rychlosti precese setrvačníku lze vyjádřit
též jako poměr velikosti B
celkového momentu hybnosti a momentu setrvačnosti
rychlosti precese setrvačníku lze vyjádřit
též jako poměr velikosti B
celkového momentu hybnosti a momentu setrvačnosti
 ;
;
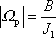 . . |
(6,88) |
Při důkazu tvrzení (6,88) vyjdeme z rovnice (6,87)
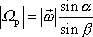 . . |
Dle rovnice
(6,55)
moment setrvačnosti vůči ose otáčení
násobený úhlovou rychlostí otáčení kolem osy je roven průmětu celkového momentu
hybnosti
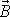 do osy otáčení, neboli (viz obr.72)
do osy otáčení, neboli (viz obr.72)
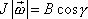 , , |
kde J je moment setrvačnosti setrvačníku vůči okamžité, tj. vektorem
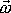 proložené ose otáčení. Dosadíme-li dle poslední rovnice za
proložené ose otáčení. Dosadíme-li dle poslední rovnice za
 do
(6,87)
, dostáváme
do
(6,87)
, dostáváme
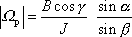 . . |
Úhel
 . Rozepíšeme
. Rozepíšeme
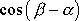 , poměr
, poměr
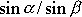 nahradíme výrazem
nahradíme výrazem
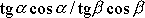 a za
a za
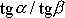 dosadíme dle
(6,84)
, dostaneme
dosadíme dle
(6,84)
, dostaneme
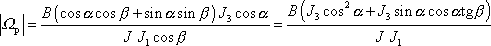 . . |
Jelikož dle
(6,84)
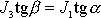 a
a
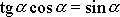 , lze dále psát
, lze dále psát
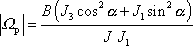 . . |
Např. z obr.71 je zřejmé, že
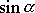 a
a
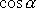 lze pokládat za složky jednotkového vektoru
ve směru okamžité osy otáčení, volíme-li soustavu souřadnic spjatou
s tělesem tak, že osa
lze pokládat za složky jednotkového vektoru
ve směru okamžité osy otáčení, volíme-li soustavu souřadnic spjatou
s tělesem tak, že osa
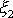 je kolmá k obrázku. (U symetrického
setrvačníku momenty setrvačnosti vůči všem osám procházejícím hmotným středem
kolmo k ose symetrie setrvačníku jsou stejné, a proto shora provedená
argumentace je přípustná.) Potom dle
(6,60)
výraz v závorce
v poslední rovnici
je kolmá k obrázku. (U symetrického
setrvačníku momenty setrvačnosti vůči všem osám procházejícím hmotným středem
kolmo k ose symetrie setrvačníku jsou stejné, a proto shora provedená
argumentace je přípustná.) Potom dle
(6,60)
výraz v závorce
v poslední rovnici
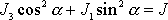 , a tedy
, a tedy
 , jak jsme měli dokázat.
, jak jsme měli dokázat.
Odvodíme vztahy mezi velikostmi rychlosti precese
 v tělese, rychlosti precese
v prostoru
v tělese, rychlosti precese
v prostoru
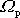 a rychlosti vlastní rotace setrvačníku
a rychlosti vlastní rotace setrvačníku
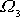 . Abychom se vyhnuli zdlouhavějším úpravám trigonometrických funkcí, budeme
předpokládat, že úhly
. Abychom se vyhnuli zdlouhavějším úpravám trigonometrických funkcí, budeme
předpokládat, že úhly
 jsou malé. Jelikož
jsou malé. Jelikož
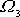 je třetí složka vektoru
je třetí složka vektoru
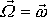 v soustavě spjaté se setrvačníkem,
zřejmě platí
v soustavě spjaté se setrvačníkem,
zřejmě platí
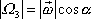 . . |
Dosadíme-li poslední vztah do rovnice (6,87) , dostáváme
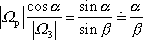 . . |
Dle (6,84)
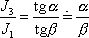 , , |
a tedy
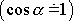
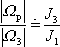 . . |
(6,89) |
Dosadíme-li do poslední přibližné rovnice za
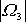 dle
(6,85)
, dostaneme
dle
(6,85)
, dostaneme
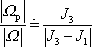 . . |
(6,90) |
Jsou-li hodnoty
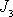 a
a
 navzájem blízké, je
navzájem blízké, je
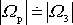 a
a
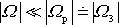 . Precese v prostoru je přibližně stejně rychlá jako rychlost vlastní rotace
setrvačníku a rychlost precese v tělese
. Precese v prostoru je přibližně stejně rychlá jako rychlost vlastní rotace
setrvačníku a rychlost precese v tělese
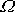 je velmi malá. Je-li
je velmi malá. Je-li
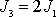 , je velikost precesní úhlové rychlosti
, je velikost precesní úhlové rychlosti
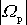 dvojnásobkem velikosti rotační rychlosti
setrvačníku
dvojnásobkem velikosti rotační rychlosti
setrvačníku
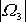 a precesní rychlost v prostoru
a precesní rychlost v prostoru
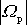 je dvojnásobkem precesní rychlosti
v tělese
je dvojnásobkem precesní rychlosti
v tělese
 .
.
Oba uvažované případy se podstatně liší od vztahů, které v příštím článku získáme při vyšetřování pseudoregulární precese těžkého symetrického setrvačníku. Pro těžký setrvačník budeme vždy předpokládat, že vlastní rotační rychlost setrvačníku je podstatně vyšší než úhlová rychlost precese setrvačníku v prostoru. O rychlosti precese v tělese nebudeme (s výjimkou zmínky o nutaci) vůbec uvažovat.
Probereme ještě dva zvláštní
případy volby počáteční úhlové rychlosti otáčení
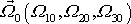 , tj. volby osy podél které a velikosti rychlosti jakou setrvačník roztočíme, než
jej necháme volně (bez působení sil) dále rotovat.
, tj. volby osy podél které a velikosti rychlosti jakou setrvačník roztočíme, než
jej necháme volně (bez působení sil) dále rotovat.
Jsou-li v čase
 ,
,
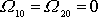 , pak z rovnic
(6,80)
a
(6,81)
plyne
, pak z rovnic
(6,80)
a
(6,81)
plyne
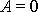 , a složky
, a složky
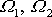 vektoru úhlové rychlosti otáčení
v soustavě souřadnic spjaté s tělesem jsou nulové po celou dobu
pohybu setrvačníku. Z rovnice
(6,83)
dostáváme
vektoru úhlové rychlosti otáčení
v soustavě souřadnic spjaté s tělesem jsou nulové po celou dobu
pohybu setrvačníku. Z rovnice
(6,83)
dostáváme
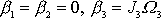 . V uvažovaném speciálním případě je moment hybnosti
. V uvažovaném speciálním případě je moment hybnosti
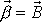 rovnoběžný s úhlovou rychlostí
rovnoběžný s úhlovou rychlostí
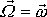 . Osa otáčení má v tělese i prostoru stálý směr a setrvačník kolem ní rotuje
konstantní úhlovou rychlostí
. Osa otáčení má v tělese i prostoru stálý směr a setrvačník kolem ní rotuje
konstantní úhlovou rychlostí
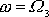 . Roztočíme-li symetrický setrvačník kolem jeho osy symetrie, rotace kolem této
osy se jak v prostoru tak v tělese udržuje. Setrvačník se otáčí
jednoduchým způsobem naznačeným na obr.74.
. Roztočíme-li symetrický setrvačník kolem jeho osy symetrie, rotace kolem této
osy se jak v prostoru tak v tělese udržuje. Setrvačník se otáčí
jednoduchým způsobem naznačeným na obr.74.
 Je-li v čase
Je-li v čase
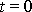 ,
,
 , je dle
(6,77)
tato složka úhlové rychlosti nulová po celou dobu pohybu. Z
(6,78)
pak dostáváme
, je dle
(6,77)
tato složka úhlové rychlosti nulová po celou dobu pohybu. Z
(6,78)
pak dostáváme
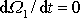 a
a
 ; složky
; složky
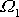 ,
,
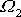 úhlové rychlosti
úhlové rychlosti
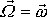 mají po celou dobu pohybu stejnou hodnotu
jako v čase
mají po celou dobu pohybu stejnou hodnotu
jako v čase
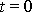 . Při počátečních podmínkách
. Při počátečních podmínkách
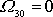 ,
,
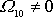 ,
,
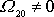 má osa otáčení v tělese stálou polohu
v rovině kolmé k ose symetrie setrvačníku. Z rovnice
(6,83)
plyne
má osa otáčení v tělese stálou polohu
v rovině kolmé k ose symetrie setrvačníku. Z rovnice
(6,83)
plyne
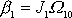 ,
,
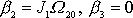 , tedy vektory
, tedy vektory
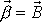 a
a
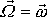 jsou rovnoběžné. Těleso se otáčí kolem osy,
jejíž poloha je v prostoru stálá.
jsou rovnoběžné. Těleso se otáčí kolem osy,
jejíž poloha je v prostoru stálá.
V obou uvažovaných zvláštních případech rotuje symetrický volný setrvačník kolem hlavních os setrvačnosti procházejících jeho hmotným středem, které v tělese i v prostoru zachovávají svůj směr.
Osa tělesa, vůči níž může těleso udržovat stálou rotaci, aniž je osa rotace udržována vazbami, se nazývá volnou osou . U kulového setrvačníku všechny osy procházející hmotným středem jsou volné osy. U symetrického setrvačníku jsou volnými osami osa symetrie a všechny osy k ní kolmé procházející hmotným středem.
Vyšetříme stabilitu rotace kolem volných os symetrického
setrvačníku. Mějme setrvačník rotující kolem volné osy. Osa stálá v tělese
i v prostoru má směr celkového momentu hybnosti
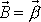 . Chceme-li osu vychýlit, musíme na ni působit nenulovým momentem
. Chceme-li osu vychýlit, musíme na ni působit nenulovým momentem
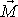 sil, např. dvojicí sil
sil, např. dvojicí sil
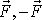 znázorněnou na obr.75. Směr momentu
znázorněnou na obr.75. Směr momentu
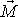 je kolmý k vektorům
je kolmý k vektorům
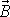 a
a
 .
.
Dle druhé věty impulsové
(5,49)
 . Pro krátkodobé působení můžeme pokládat moment síly
. Pro krátkodobé působení můžeme pokládat moment síly
 za konstantní a psát vztah mezi diferencemi
za konstantní a psát vztah mezi diferencemi
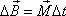 . . |
(6,91) |
Přírůstek momentu hybnosti
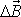 za čas
za čas
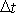 je rovnoběžný s
je rovnoběžný s
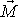 , a tedy kolmý k
, a tedy kolmý k
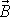 . Je-li
. Je-li
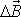 kolmé k
kolmé k
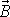 , nemění se v prvním přiblížení velikosti vektoru
, nemění se v prvním přiblížení velikosti vektoru
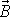 , ale mění se pouze jeho směr. Dle rovnice
(6,40)
, ale mění se pouze jeho směr. Dle rovnice
(6,40)
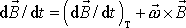 . Před působením momentu síly
. Před působením momentu síly
 , tj. na začátku časového intervalu
, tj. na začátku časového intervalu
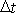 , je
, je
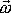 rovnoběžné s
rovnoběžné s
 a tedy
a tedy
 . V uvažovaném prvním přiblížení je pak změna
. V uvažovaném prvním přiblížení je pak změna
 momentu hybnosti
momentu hybnosti
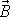 v prostoru a v tělese stejná. Na
konci časového intervalu
v prostoru a v tělese stejná. Na
konci časového intervalu
 nový moment hybnosti
nový moment hybnosti
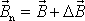 nebude již mít směr volné
nebude již mít směr volné
 osy, tj.
některé z hlavních os setrvačnosti tělesa. Osa symetrie setrvačníku po
odstranění působících vnějších sil začne konat kolem směru nového momentu
hybnosti
osy, tj.
některé z hlavních os setrvačnosti tělesa. Osa symetrie setrvačníku po
odstranění působících vnějších sil začne konat kolem směru nového momentu
hybnosti
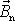 regulární precesi.
regulární precesi.
O impulsu momentu síly
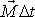 předpokládáme, že je malý a tedy i vychýlení
okamžité osy otáčení setrvačníku jím způsobené je malé.
předpokládáme, že je malý a tedy i vychýlení
okamžité osy otáčení setrvačníku jím způsobené je malé.
Nejprve předpokládejme, že setrvačník před aplikací
impulsu
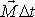 rotoval kolem své osy symetrie. Po aplikaci
impulsu
rotoval kolem své osy symetrie. Po aplikaci
impulsu
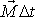 začne osa symetrie setrvačníku precedovat
s malým úhlem
začne osa symetrie setrvačníku precedovat
s malým úhlem
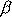 (viz. obr.72) vůči směru vektoru
(viz. obr.72) vůči směru vektoru
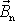 . Jelikož precesní úhel
. Jelikož precesní úhel
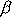 a odklon
a odklon
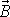 a
a
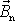 jsou malé, budou se i po aplikaci impulsu
jsou malé, budou se i po aplikaci impulsu
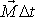 osa symetrie setrvačníku a okamžitá osa
otáčení setrvačníku pohybovat v blízkosti původní osy otáčení setrvačníku.
osa symetrie setrvačníku a okamžitá osa
otáčení setrvačníku pohybovat v blízkosti původní osy otáčení setrvačníku.
Byla-li hlavní osa, vůči které setrvačník rotoval před
aplikací momentu
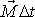 , osa kolmá k ose symetrie setrvačníku, setrvačník také začne konat
regulární precesi kolem směru
, osa kolmá k ose symetrie setrvačníku, setrvačník také začne konat
regulární precesi kolem směru
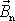 . Regulární precesi však koná osa symetrie setrvačníku a ne osa, vůči které
setrvačník před aplikací impulsu
. Regulární precesi však koná osa symetrie setrvačníku a ne osa, vůči které
setrvačník před aplikací impulsu
 rotoval. Proto v tomto druhém případě aplikace i malého
impulsu
rotoval. Proto v tomto druhém případě aplikace i malého
impulsu
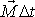 způsobí, že okamžitá osa otáčení setrvačníku
se od původní osy otáčení bude v dalším průběhu pohybu velmi značně
vzdalovat.
způsobí, že okamžitá osa otáčení setrvačníku
se od původní osy otáčení bude v dalším průběhu pohybu velmi značně
vzdalovat.
Závěry právě provedených úvah lze formulovat tak, že rotace kolem osy symetrie setrvačníku je stabilní, zatímco rotace kolem hlavní osy kolmé k ose symetrie setrvačníku je nestabilní. Při praktické aplikaci tohoto závěru je však třeba opatrnosti. Označíme tuto stabilitu jako stabilitu v geometrickém smyslu a před vyslovením závěrů o stabilitě rotace setrvačníků rozebereme stabilitu rotace setrvačníků ještě z energetického hlediska.
Nejdříve budeme z hlediska energie uvažovat stabilitu
rotace symetrického setrvačníku kolem hlavních os. Při rozboru rovnice
(6,91)
jsme ukázali, že krátkodobé působení momentu síly
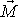 kolmého k ose otáčení setrvačníku nemění velikost
kolmého k ose otáčení setrvačníku nemění velikost
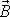 celkového momentu hybnosti setrvačníku. Čtverec
celkového momentu hybnosti setrvačníku. Čtverec
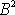 velikosti momentu hybnosti na začátku časového intervalu
velikosti momentu hybnosti na začátku časového intervalu
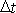 , po který působí moment
, po který působí moment
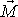 , je
, je
 , na konci intervalu
, na konci intervalu
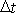 je
je
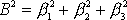 . Poslední výraz pro
. Poslední výraz pro
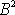 můžeme upravit dle
(6,83)
,
(6,80)
a
(6,81)
,
dostaneme
můžeme upravit dle
(6,83)
,
(6,80)
a
(6,81)
,
dostaneme
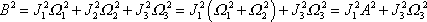 . . |
Má-li být velikost momentu hybnosti zachována, musí platit
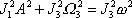 . . |
(6,92) |
Dle vyjádření
(6,69)
dvojnásobek kinetické energie na
začátku intervalu
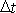 je
je
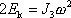 |
(6,93) |
a na konci časového intervalu
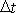 nová hodnota dvojnásobku kinetické energie je
nová hodnota dvojnásobku kinetické energie je
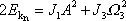 . . |
(6,94) |
Vynásobíme-li výraz
(6,93)
momentem setrvačností
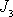 , dostaneme pravou stranu rovnice
(6,92)
, vynásobíme-li hodnotou
, dostaneme pravou stranu rovnice
(6,92)
, vynásobíme-li hodnotou
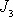 rovnici
(6,94)
, dostaneme
rovnici
(6,94)
, dostaneme
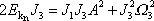 . . |
(6,95) |
Výraz
(6,95)
je větší než levá strana rovnice
(6,92)
, když
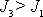 a menší než levá strana rovnice
(6,92)
, když
a menší než levá strana rovnice
(6,92)
, když
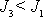 ; tedy
; tedy
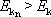 |
pro
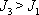 |
(6,96) |
a
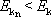 |
pro
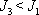 . . |
(6,97) |
Dle věty
(5,65)
práce vykonaná vnějšími silami na těleso je
rovna přírůstku kinetické energie tělesa. V případě
(6,96)
je tato práce
kladná. Abychom vychýlili setrvačník z rotace kolem jeho osy symetrie,
musíme vynaložit kladnou práci, když moment setrvačnosti kolem osy
symetrie
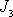 je větší než druhý hlavní moment setrvačnosti
je větší než druhý hlavní moment setrvačnosti
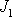 . V případě, kdy
. V případě, kdy
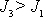 , je rotace setrvačníku kolem jeho osy symetrie z energetického hlediska
stabilní. V případě
(6,97)
je práce vykonaná vnějšími silami na vychýlení
setrvačníku záporná. Je-li
, je rotace setrvačníku kolem jeho osy symetrie z energetického hlediska
stabilní. V případě
(6,97)
je práce vykonaná vnějšími silami na vychýlení
setrvačníku záporná. Je-li
 , je rotace setrvačníku kolem jeho osy symetrie z energetického hlediska
labilní.
, je rotace setrvačníku kolem jeho osy symetrie z energetického hlediska
labilní.
Rotuje-li setrvačník kolem volné osy kolmé k ose symetrie setrvačníku, rovnice analogická rovnici (6,92) má tvar
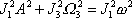 , , |
(6,92) |
rovnice analogická rovnici (6,93) má tvar
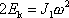 |
(6,93) |
a rovnice analogická rovnici (6,94) je formálně shodná
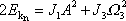 . . |
(6,94) |
Porovnáním rovnic
(6,92)
,
(6,93)
a
(6,94)
získáme stejným
způsobem (násobení
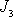 nahra-díme násobením
nahra-díme násobením
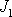 ) jako u nečárkových rovnic nerovnosti
) jako u nečárkových rovnic nerovnosti
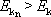 |
pro
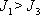 |
(6,96) |
a
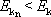 |
pro
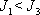 . . |
(6,97) |
Z nerovností
(6,96)
a
(6,97)
plyne, že rotace kolem
hlavní osy kolmé k ose symetrie setrvačníku je z energetického
hlediska stabilní pro
 a nestabilní pro
a nestabilní pro
 . Energetickou stabilitu a nestabilitu jsme takto určili pro odchylku osy
z polohy kolmé k ose symetrie setrvačníku. Rotace kolem všech
hlavních os kolmých k ose symetrie setrvačníku je z energetického
hlediska ekvivalentní, poloha osy rotace v rovině kolmé k ose
symetrie setrvačníku je energeticky indiferentní.
. Energetickou stabilitu a nestabilitu jsme takto určili pro odchylku osy
z polohy kolmé k ose symetrie setrvačníku. Rotace kolem všech
hlavních os kolmých k ose symetrie setrvačníku je z energetického
hlediska ekvivalentní, poloha osy rotace v rovině kolmé k ose
symetrie setrvačníku je energeticky indiferentní.
Z energetického hlediska stabilní rotace symetrického setrvačníku nastane, když setrvačník rotuje kolem hlavní osy, vůči které má největší moment setrvačnosti. Tento závěr bývá demonstrován pokusně. Rotačně symetrické homogenní těleso roztočíme kolem libovolné osy. Vlivem nahodilých vnějších silových impulsů začne po jisté době těleso rotovat kolem volné osy, vůči níž má největší moment setrvačnosti. Např. disk začne rotovat kolem osy rotační symetrie, podlouhlý úzký váleček kolem osy kolmé k ose rotační symetrie. Demonstrační pokusy uvedeného druhu bývají označovány jako pokusy na volnou osu rotace.
Pohyb asymetrického volného setrvačníku lze stanovit řešením
rovnic
(6,71)
. Rovnice jsou řešitelné i pro tento obecný případ, kdy všechny
tři hlavní momenty setrvačnosti
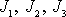 setrvačníku jsou vzájemně různé (řešení je
podáno např. v [11], [12], [13], [14]).
Řešení je však dosti obtížné a pro jeho interpretaci je nutno zavést vhodné
vyjádření vzájemného postavení soustavy souřadné pevné v tělese a soustavy
souřadné pevné v prostoru. Takové vyjádření se děje zavedením obecných
souřadnic určujících pohyb tělesa. Nejčastěji se za obecné souřadnice
rotujícího tuhého tělesa (setrvačníku) volí Eulerovy úhly
. Způsob jejich zavedení je popsán ve všech
v tomto odstavci citovaných knihách a též ve skriptech [16].
setrvačníku jsou vzájemně různé (řešení je
podáno např. v [11], [12], [13], [14]).
Řešení je však dosti obtížné a pro jeho interpretaci je nutno zavést vhodné
vyjádření vzájemného postavení soustavy souřadné pevné v tělese a soustavy
souřadné pevné v prostoru. Takové vyjádření se děje zavedením obecných
souřadnic určujících pohyb tělesa. Nejčastěji se za obecné souřadnice
rotujícího tuhého tělesa (setrvačníku) volí Eulerovy úhly
. Způsob jejich zavedení je popsán ve všech
v tomto odstavci citovaných knihách a též ve skriptech [16].
Při geometrické interpretaci pohybu asymetrického setrvačníku znovu můžeme použít názorné představy odvalování. Pohyb lze vyjádřit jako odvalování elipsoidu pevného v setrvačníku po rovině pevné v prostoru. Musíme znát, který bod elipsoidu se dotýká kterého bodu roviny. Čáru tvořenou dotykovými body na elipsoidu pevném v setrvačníku nazýváme polodií, čáru tvořenou dotykovými body na rovině pevné v prostoru nazýváme herpolodií.
Hlavní osy setrvačnosti jsou volnými osami i pro asymetrický
setrvačník. Položíme-li v první z rovnic
(6,71)
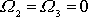 , dostáváme
, dostáváme
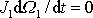 , odkud
, odkud
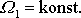 . Potom postupem stejným jako pro symetrický setrvačník lze dokázat, že moment
hybnosti
. Potom postupem stejným jako pro symetrický setrvačník lze dokázat, že moment
hybnosti
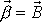 je rovnoběžný s úhlovou rychlostí
otáčení
je rovnoběžný s úhlovou rychlostí
otáčení
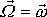 setrvačníku; osa rotace je v tělese i
v prostoru stálá. Ze symetrie rovnic
(6,71)
plyne, že obdobné závěry platí
i pro rotaci kolem zbývajících dvou hlavních os setrvačnosti. Rozborem
provedeným např. v [11], [12] lze
ukázat, že rotace kolem hlavní osy, vůči níž moment setrvačnosti (označíme
jej
setrvačníku; osa rotace je v tělese i
v prostoru stálá. Ze symetrie rovnic
(6,71)
plyne, že obdobné závěry platí
i pro rotaci kolem zbývajících dvou hlavních os setrvačnosti. Rozborem
provedeným např. v [11], [12] lze
ukázat, že rotace kolem hlavní osy, vůči níž moment setrvačnosti (označíme
jej
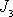 ) je největší, a rotace kolem hlavní osy,
vůči níž moment setrvačnosti (označíme jej
) je největší, a rotace kolem hlavní osy,
vůči níž moment setrvačnosti (označíme jej
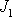 ) je nejmenší, jsou stabilní ve výše
vyloženém geometrickém smyslu. Vychýlí-li se osa rotace poněkud ze své polohy
v hlavní ose setrvačnosti, pohybuje se i nadále v blízkosti hlavní
osy. Pro hlavní osu, vůči níž moment setrvačnosti (označíme jej
) je nejmenší, jsou stabilní ve výše
vyloženém geometrickém smyslu. Vychýlí-li se osa rotace poněkud ze své polohy
v hlavní ose setrvačnosti, pohybuje se i nadále v blízkosti hlavní
osy. Pro hlavní osu, vůči níž moment setrvačnosti (označíme jej
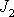 ) má prostřední hodnotu,
) má prostřední hodnotu,
 , rotace v geometrickém smyslu stabilní není. V energetickém smyslu je
stabilní rotace kolem osy, vůči níž moment setrvačnosti (zde
, rotace v geometrickém smyslu stabilní není. V energetickém smyslu je
stabilní rotace kolem osy, vůči níž moment setrvačnosti (zde
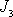 ) je největší. Rychle roztočené těleso
libovolného tvaru vlivem náhodných vnějších silových impulsů po delší době
začne rotovat kolem hlavní osy setrvačnosti, vůči které má největší moment
setrvačnosti. Výše zmíněné pokusy na volnou osu rotace mohou být úspěšně
prováděny s tělesy libovolného tvaru, nejen s rotačně symetrickými
tělesy.
) je největší. Rychle roztočené těleso
libovolného tvaru vlivem náhodných vnějších silových impulsů po delší době
začne rotovat kolem hlavní osy setrvačnosti, vůči které má největší moment
setrvačnosti. Výše zmíněné pokusy na volnou osu rotace mohou být úspěšně
prováděny s tělesy libovolného tvaru, nejen s rotačně symetrickými
tělesy.
Úvahy o stabilitě rotace můžeme shrnout takto:
Stabilita rotace v geometrickém smyslu předpokládá dokonalé splnění podmínek volného (bezsilového) pohybu tělesa. Při pohybu reálných těles vždy k silové interakci s okolím dochází. Proto jsou důležitější energetické úvahy o stabilitě rotace tělesa, z kterých vyplývá, že nejstabilnější je rotace tělesa kolem hlavní osy, vůči které má těleso největší moment setrvačnosti.
Všechny pohyby volných setrvačníků
jsou pohyby tuhého tělesa, pro něž výslednice vnějších sil a výsledný moment
vnějších sil působící na těleso jsou nulové. Takové těleso je v rovnováze.
Hmotný střed tělesa, které je v rovnováze, může být v klidu nebo
v rovnoměrném přímočarém pohybu, jak jsme ukázali v čl.5.8. Kolem
hmotného středu může těleso konat některý z pohybů popsaných v tomto
článku. Má-li tensor momentu setrvačnosti tělesa pro hmotný střed všechny tři
hlavní momenty setrvačnosti
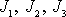 vzájemně různé, může těleso kolem hmotného
středu konat zde podrobně nepopsaný pohyb asymetrického setrvačníku. I při
splnění podmínek rovnováhy může těleso, které nebylo původně v klidu,
konat takto složitý pohyb.
vzájemně různé, může těleso kolem hmotného
středu konat zde podrobně nepopsaný pohyb asymetrického setrvačníku. I při
splnění podmínek rovnováhy může těleso, které nebylo původně v klidu,
konat takto složitý pohyb.