Rovnici (4,122) pro vynucený harmonický kmit napíšeme v poněkud pozměněné a obecnější formě
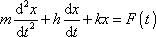 . . |
(4,192) |
Na pravé straně rovnice
(4,192)
je obecná funkce
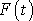 udávající časový průběh síly a konstanty h
a k mají obvyklý význam daný rovnicemi
(4,68)
a
(4,69)
. Je-li funkce
udávající časový průběh síly a konstanty h
a k mají obvyklý význam daný rovnicemi
(4,68)
a
(4,69)
. Je-li funkce
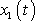 řešením rovnice
(4,192)
pro zadanou sílu
řešením rovnice
(4,192)
pro zadanou sílu
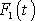 a funkce
a funkce
 řešením téže rovnice pro sílu
řešením téže rovnice pro sílu
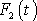 , je funkce
, je funkce
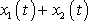 řešením rovnice
(4,192)
pro zadanou sílu
řešením rovnice
(4,192)
pro zadanou sílu
 . Sečteme-li rovnice
. Sečteme-li rovnice
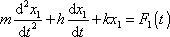 |
a
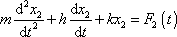 , , |
vyjadřující, že
 a
a
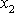 jsou pro
jsou pro
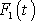 a
a
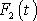 řešením rovnice
(4,192)
, dostaneme
řešením rovnice
(4,192)
, dostaneme
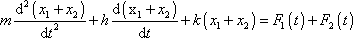 , , |
a tím je dokázáno shora vyslovené tvrzení. Říkáme, že pro
pohyb hmotného bodu, který je popsán rovnicí
(4,192)
, platí
princip superpozice. Princip
superpozice je těsně svázán s linearitou rovnice
(4,192)
. Nahradíme-li
v ní např. člen kx členem
 ,tedy uvažujeme-li rovnici
,tedy uvažujeme-li rovnici
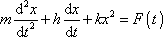 , , |
(4,193) |
lze se snadno přesvědčit, že princip superpozice neplatí. Je-li funkce
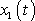 řešením rovnice
(4,193)
pro sílu
řešením rovnice
(4,193)
pro sílu
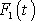 a funkce
a funkce
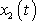 řešením téže rovnice pro sílu
řešením téže rovnice pro sílu
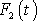 , není funkce
, není funkce
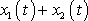 řešením rovnice
(4,193)
pro sílu
řešením rovnice
(4,193)
pro sílu
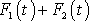 .
.
Principy superpozice jsou často užívány v různých oblastech fyziky a vždy úzce souvisejí s linearitou sledovaných problémů. Obecně lze jejich obsah vyslovit tak, že dva podněty při společném působení vyvolávají reakci rovnou součtu reakcí, jaké by podněty dávaly při samostatném působení. První podnět nesmí systém dostat do stavu, kdy na další podněty reaguje jinak než v neporušeném stavu. Poslední tvrzení je vyjádřením lineární odezvy systému na podnět ; velikost přírůstku lineární funkce odpovídající stejnému přírůstku nezávisle proměnné je stejná pro všechny hodnoty této funkce. V reálných systémech je linearita splněna jen v určitých oborech velikostí podnětů a princip superpozice platí jen v těchto oborech. Příkladem může být nastupování cestujících do autobusu. Je-li např. autobus určen pro 50 cestujících, první až asi sedmdesátý cestující nastupují stejným způsobem. Linearita a princip superpozice jsou splněny. Když se však snaží do autobusu dostat např. devadesátý cestující, způsob nastupování je již zcela jiný, linearita ani superpozice není splněna..
Platí-li pro rovnici (4,192) princip superpozice, je snadné dokázat, že platí i pro rovnici (4,122) . Řešením rovnice (4,122) v ustáleném případě jsou harmonické kmity. Působí-li na hmotný bod dvě různé vynucující síly
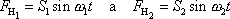 , , |
které samostatně vyvolávají v ustáleném případě harmonické kmity
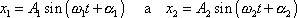 , , |
jejich společným působením vznikne dle principu superpozice pohyb
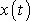 daný rovnicí
daný rovnicí
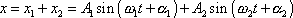 . . |
(4,194) |
Funkce
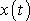 daná rovnicí
(4,194)
vznikne sečtením dvou
kmitů probíhajících podél jedné přímky. Říkáme, že rovnice
(4,194)
popisuje
skládání dvou kmitů stejného směru. S úlohou skládat kmity se nesetkáváme
jenom při vyšetřování pohybu hmotného bodu, ale též, když skládáme elektrické
kmity, když vyšetřujeme interferenci vlnění v jednom místě prostoru a
v řadě dalších případů. I na tyto případy lze aplikovat, ověříme-li
platnost příslušných superpozičních principů, výsledky, které dále odvodíme pro
skládání kmitů hmotného bodu.
daná rovnicí
(4,194)
vznikne sečtením dvou
kmitů probíhajících podél jedné přímky. Říkáme, že rovnice
(4,194)
popisuje
skládání dvou kmitů stejného směru. S úlohou skládat kmity se nesetkáváme
jenom při vyšetřování pohybu hmotného bodu, ale též, když skládáme elektrické
kmity, když vyšetřujeme interferenci vlnění v jednom místě prostoru a
v řadě dalších případů. I na tyto případy lze aplikovat, ověříme-li
platnost příslušných superpozičních principů, výsledky, které dále odvodíme pro
skládání kmitů hmotného bodu.
Určíme tvar funkce
 dané rovnicí
(4,194)
pro dva speciální
případy. Nejprve složíme dva kmity
dané rovnicí
(4,194)
pro dva speciální
případy. Nejprve složíme dva kmity
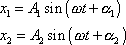 , , |
které mají stejnou frekvenci
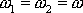 , různou amplitudu
, různou amplitudu
 a různou fázi (pro fázové konstanty platí nerovnost
a různou fázi (pro fázové konstanty platí nerovnost
 ). Dostáváme
). Dostáváme
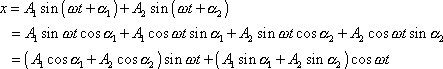 , , |
a tedy dle vztahů (1,30)
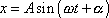 , , |
kde
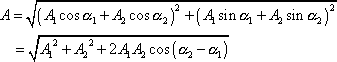 |
(4,195) |
a
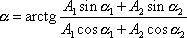 . . |
(4,196) |
Složením dvou kmitů stejné frekvence vznikne kmit téže
frekvence, jehož amplituda je dána rovnicí
(4,195)
a fázová konstanta rovnicí
(4,196)
. Je-li
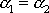 , má výsledný kmit amplitudu rovnu součtu amplitud výchozích kmitů
, má výsledný kmit amplitudu rovnu součtu amplitud výchozích kmitů
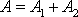 a fázovou konstantu
a fázovou konstantu
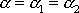 , jak plyne v tomto speciálním případě z rovnic
(4,195)
a
(4,196)
.
Nulovou hodnotu amplituda A daná rovnicí
(4,195)
bude mít pouze, když
, jak plyne v tomto speciálním případě z rovnic
(4,195)
a
(4,196)
.
Nulovou hodnotu amplituda A daná rovnicí
(4,195)
bude mít pouze, když
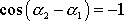 , tedy když
, tedy když
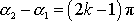 , kde k je celé číslo, a
, kde k je celé číslo, a
 . Skládají-li se dva kmity stejné amplitudy s rozdílem fázových konstant
. Skládají-li se dva kmity stejné amplitudy s rozdílem fázových konstant
 a
a
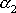 rovným např.
rovným např.
 , žádná výchylka nenastane, kmity se vzájemně ruší.
, žádná výchylka nenastane, kmity se vzájemně ruší.
Jako druhý vyšetříme případ skládání dvou kmitů, které
nemají stejnou frekvenci. Obecný případ daný rovnicí
(4,194)
zjednodušíme
předpokladem o rovnosti amplitud obou kmitů
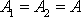 . Potom
. Potom
 a použijeme-li vzorec pro součet dvou sinů různých úhlů
a použijeme-li vzorec pro součet dvou sinů různých úhlů
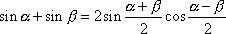 , , |
dostáváme
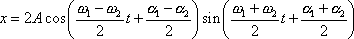 . . |
(4,197) |
Liší-li se značně
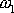 a
a
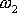 , je výraz
(4,197)
nepřehledný. Jsou-li však frekvence kmitů
, je výraz
(4,197)
nepřehledný. Jsou-li však frekvence kmitů
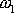 a
a
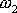 blízké (budeme předpokládat
blízké (budeme předpokládat
 ), je frekvence
), je frekvence
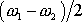 podstatně nižší než frekvence
podstatně nižší než frekvence
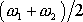 . Na výraz
(4,197)
lze pak pohlížet jako na harmonický kmit
. Na výraz
(4,197)
lze pak pohlížet jako na harmonický kmit
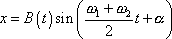 |
(4,198) |
o frekvenci
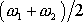 , kde místo amplitudy je časově proměnná funkce
, kde místo amplitudy je časově proměnná funkce
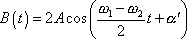 . . |
(4,199) |
 Frekvence
Frekvence
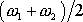 je střední frekvence kmitů
je střední frekvence kmitů
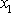 a
a
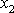 , jejichž složením pohyb
(4,198)
vznikl a
, jejichž složením pohyb
(4,198)
vznikl a
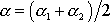 . Funkce
. Funkce
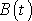 da-ná rovnicí
(4,199)
je harmonickou funkcí o frekvenci rovné poloviční hodnotě rozdílu frekvencí
da-ná rovnicí
(4,199)
je harmonickou funkcí o frekvenci rovné poloviční hodnotě rozdílu frekvencí
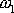 a
a
 kmitů
kmitů
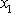 a
a
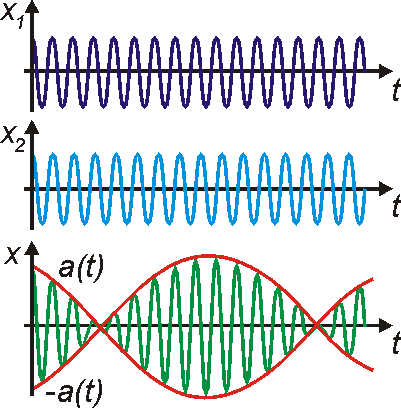
 . Na obr.32 jsou znázorněny původní kmity
. Na obr.32 jsou znázorněny původní kmity
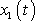 a
a
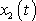 a výsledná funkce
a výsledná funkce
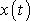 . Obálku
. Obálku
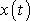 tvoří funkce
tvoří funkce
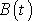 a
a
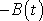 . Pokládáme-li, jak již bylo výše řečeno, funkci
. Pokládáme-li, jak již bylo výše řečeno, funkci
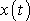 přibližně za kmit s proměnnou
amplitudou, můžeme vyslovit závěr. Složením dvou kmitů blízké frekvence vznikne
kmit střední frekvence, jehož amplituda se mění s rozdílovou frekvencí
přibližně za kmit s proměnnou
amplitudou, můžeme vyslovit závěr. Složením dvou kmitů blízké frekvence vznikne
kmit střední frekvence, jehož amplituda se mění s rozdílovou frekvencí
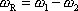 |
(4,200) |
obou původních kmitů. Funkce
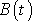 na rozdíl od skutečné amplitudy může být kladná i záporná. Maximální amplituda kmitu x
daného rovnicí
(4,198)
nastane v okolí (časovém) jak
největší kladné tak i záporné hodnoty funkce
(4,199)
. Frekvence změny amplitudy
kmitu
(4,198)
je tedy
na rozdíl od skutečné amplitudy může být kladná i záporná. Maximální amplituda kmitu x
daného rovnicí
(4,198)
nastane v okolí (časovém) jak
největší kladné tak i záporné hodnoty funkce
(4,199)
. Frekvence změny amplitudy
kmitu
(4,198)
je tedy
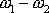 a ne
a ne
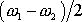 , jak by naznačoval zběžný pohled na rovnici
(4,198)
(viz též obr.32). Říkáme, že
složením dvou kmitů blízké frekvence vznikají rázy
o frekvenci rázů dané rovnicí
(4,200)
. Pro lineární frekvenci
, jak by naznačoval zběžný pohled na rovnici
(4,198)
(viz též obr.32). Říkáme, že
složením dvou kmitů blízké frekvence vznikají rázy
o frekvenci rázů dané rovnicí
(4,200)
. Pro lineární frekvenci
V celém výkladu kmitů nazýváme úhlovou frekvenci stručně frekvencí, a proto zde pro odlišení frekvenci f zavedenou rovnicí (1,27) označujeme jako lineární frekvenci.
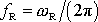 , tj. pro počet zesílení a zeslabení kmitu
(4,198)
za jednotku času, platí zřejmě vztah
, tj. pro počet zesílení a zeslabení kmitu
(4,198)
za jednotku času, platí zřejmě vztah
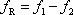 , , |
(4,201) |
kde
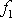 a
a
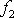 jsou lineární frekvence kmitů
jsou lineární frekvence kmitů
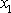 a
a
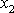 .
.
Vznik rázů lze pozorovat např. při současném znění dvou
blízkých akustických tónů. Čím bližší tóny, tím je frekvence rázů nižší. Při
rovnosti frekvencí obou tónů rázy vymizí. Tohoto jevu se užívá při ladění
hudebních nástrojů. Obdobně lze sledovat frekvence dvou generátorů střídavých
elektrických napětí. Přivedeme-li např. napětí ze dvou generátorů přibližně
stejné frekvence na svislé vychylující destičky osciloskopu, získáme na obrazovce
obraz odpovídající funkci
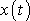 znázorněné na obr.32. Při slaďování
frekvence se prodlužují vzdálenosti mezi uzlovými body obálky funkce
znázorněné na obr.32. Při slaďování
frekvence se prodlužují vzdálenosti mezi uzlovými body obálky funkce
 . Dalším slaďováním dochází na obrazovce již pouze k pomalému pulzování
amplitudy kmitů o frekvenci
. Dalším slaďováním dochází na obrazovce již pouze k pomalému pulzování
amplitudy kmitů o frekvenci
 a úplné sladění by se projevilo klidným obrazem kmitů o frekvenci
a úplné sladění by se projevilo klidným obrazem kmitů o frekvenci
 .
.
Když jsme ukázali, jak lze skládat kmity působící podél jedné přímky, přistoupíme nyní ke skládání kmitů vzájemně kolmých. Koná-li hmotný bod ve směru x -ové osy kartézské soustavy souřadnic kmit
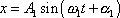 |
(4,202) |
a ve směru y-ové osy kmit
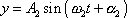 , , |
(4,203) |
jsou rovnice
(4,202)
a
(4,203)
parametrickými rovnicemi
pohybu hmotného bodu, je-li splněn princip superpozice. Princip superpozice
v tomto případě musí zabezpečit, aby pohyby hmotného bodu ve směru
osy x podél úseček
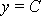 ,
,
 byly stejné pro všechna C z intervalu
byly stejné pro všechna C z intervalu
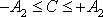 , tj. aby pohyb podél všech těchto úseček mohl být popsán stejnou rovnicí kmitu
(4,202)
. Obdobná podmínka musí být splněna i pro pohyb ve směru osy y
v pásmu
, tj. aby pohyb podél všech těchto úseček mohl být popsán stejnou rovnicí kmitu
(4,202)
. Obdobná podmínka musí být splněna i pro pohyb ve směru osy y
v pásmu
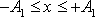 . Je-li splněn princip superpozice, úloha najít kmit daný složením kmitů
(4,202)
a
(4,203)
se redukuje na úlohu stanovit dráhu parametricky zadaného pohybu, tj.
úlohu, která se řešila v 1. kapitole. Aby nedošlo k záměně se skládáním
dvou rovnoběžných kmitů
. Je-li splněn princip superpozice, úloha najít kmit daný složením kmitů
(4,202)
a
(4,203)
se redukuje na úlohu stanovit dráhu parametricky zadaného pohybu, tj.
úlohu, která se řešila v 1. kapitole. Aby nedošlo k záměně se skládáním
dvou rovnoběžných kmitů
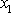 a
a
 , které bylo probráno v minulé stati, budeme v této stati značit
kartézské souřadnice v rovině x a y
namísto v kapitole 1 užívaného označení
, které bylo probráno v minulé stati, budeme v této stati značit
kartézské souřadnice v rovině x a y
namísto v kapitole 1 užívaného označení
 .
.
Nejprve složíme dva kmity stejné frekvence
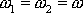
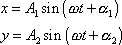 |
(4,204) |
neboli
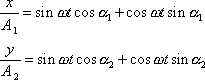 . . |
Právě napsané rovnice lze pokládat za dvě rovnice pro neznámé funkce
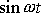 a
a
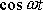 . Jejich řešením dostaneme
. Jejich řešením dostaneme
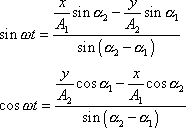 . . |
(4,205) |
Je-li
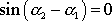 , což nastane pro
, což nastane pro
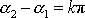 , kde k je celé číslo, dostáváme přímo z rovnic
(4,204)
, kde k je celé číslo, dostáváme přímo z rovnic
(4,204)
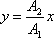 |
(4,206) |
pro
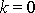 nebo k sudé a
nebo k sudé a
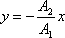 , , |
(4,207) |
když k
je liché číslo. Rovnice
(4,206)
a
(4,207)
jsou rovnicemi úseček, neboť x
se v nich mění pouze v intervalu
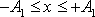 .
.
Pro ostatní hodnoty rozdílu
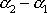 získáme křivku složených kmitů,
umocníme-li rovnice
(4,205)
na druhou a
sečteme je. Po úpravě dostaneme
získáme křivku složených kmitů,
umocníme-li rovnice
(4,205)
na druhou a
sečteme je. Po úpravě dostaneme
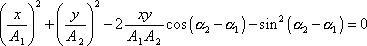 . . |
(4,208) |
Rovnice (4,208) je rovnicí kuželosečky a jelikož z rovnice (4,204) je zřejmé, že hodnoty x a y jsou omezené, jedná se o rovnici elipsy. Vynásobíme-li konstantu stojící u x2 v rovnici (4,208) konstantou u y2 a od součinu odečteme čtverec poloviční hodnoty konstanty u xy, dostaneme
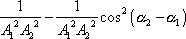 . . |
(4,209) |
Výraz
(4,209)
je s výjimkou
již dříve vyloučeného případu
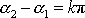 kladný a jeho kladná hodnota je dalším
důkazem (viz např.
kladný a jeho kladná hodnota je dalším
důkazem (viz např.
 , kap.5), že rovnice
(4,208)
je rovnicí elipsy.
, kap.5), že rovnice
(4,208)
je rovnicí elipsy.
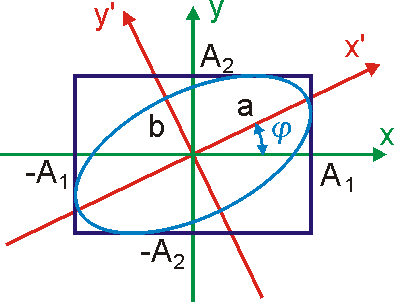 Elipsa daná rovnicí
(4,208)
je obsa-žena v obdélníku
Elipsa daná rovnicí
(4,208)
je obsa-žena v obdélníku
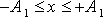 ,
,
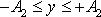 , ale její osy neleží v souřadnicových osách (viz obr.33). Nalezneme
kartézskou soustavu souřadnic
, ale její osy neleží v souřadnicových osách (viz obr.33). Nalezneme
kartézskou soustavu souřadnic
 ,
v které osy elipsy leží v souřadnicových osách . Transformační rovnice mezi soustavami
,
v které osy elipsy leží v souřadnicových osách . Transformační rovnice mezi soustavami
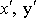 a
a
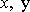 jsou (srov. rovnici
(2,17)
)
jsou (srov. rovnici
(2,17)
)
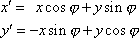 |
a inverzní transformace
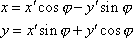 , , |
(4,210) |
kde
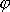 je úhel mezi kladnými směry os x a
je úhel mezi kladnými směry os x a
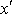 . Počátek obou souřadnicových soustav je společný.
. Počátek obou souřadnicových soustav je společný.
Když do rovnic (4,208) dosadíme za x a y dle (4,210) , dostaneme
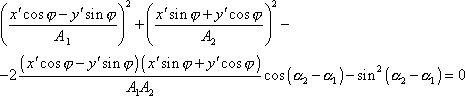 |
a po úpravě
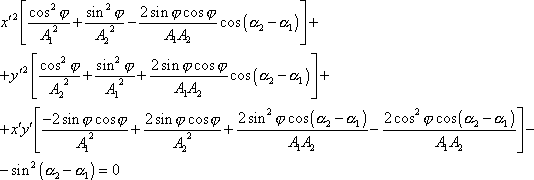 . . |
(4,211) |
V soustavě souřadnic, v níž osy elipsy jsou rovnoběžné se souřadnicovými osami, musí být možno napsat rovnici elipsy v tvaru
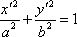 . . |
(4,212) |
Aby rovnici
(4,211)
bylo možno převést na tvar
(4,212)
, je nutné a stačí, aby koeficient u
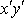 byl roven nule, tedy
byl roven nule, tedy
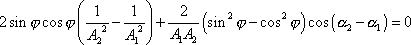 |
neboli
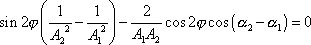 . . |
Z poslední rovnice plyne podmínka pro hledaný úhel natočení
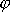 hlavní osy elipsy k ose x původní soustavy souřadnic (viz obr.33)
hlavní osy elipsy k ose x původní soustavy souřadnic (viz obr.33)
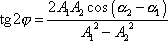 . . |
(4,213) |
Je-li úhel dán rovnicí
(4,213)
, velikost poloos elipsy a a b
lze určit, když v rovnici
(4,211)
položíme členy u
 a
a
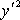 vydělené výrazem
vydělené výrazem
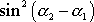 rovny
rovny
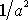 a
a
 .
.
Složením dvou vzájemně kolmých kmitů téže frekvence vznikne
elipsa s výjimkou degenerovaných případů
(4,206)
a
(4,207)
. Úhel natočení
os elipsy vzhledem ke směru původních kmitů závisí, jak plyne z rovnice
(4,213)
, na amplitudách a fázovém posunutí kmitů. Výsledek složení vzájemně
kolmých kmitů při konstantních hodnotách amplitud
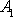 a
a
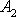 je pro několik hodnot rozdílu fázových konstant
je pro několik hodnot rozdílu fázových konstant
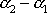 znázorněn na obr.34.
znázorněn na obr.34.
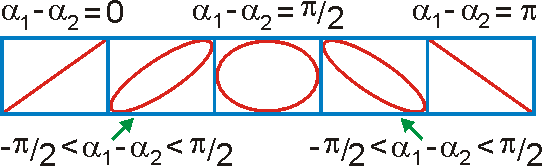
 V obecném případě, kdy frekvence
V obecném případě, kdy frekvence
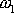 a
a
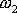 kmitů
(4,202)
a
(4,203)
nejsou stejné, vznikne jejich slože-ním křivka omezená na obdélník
SETEQS2('knihI44do_soubory/eq0144M.gif','knihI44do_soubory/eq0145M.gif','',',
kmitů
(4,202)
a
(4,203)
nejsou stejné, vznikne jejich slože-ním křivka omezená na obdélník
SETEQS2('knihI44do_soubory/eq0144M.gif','knihI44do_soubory/eq0145M.gif','',',
','.','1.13','.34');
Jsou-li frekvence
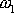 a
a
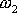 v poměru malých celých čísel m a n
v poměru malých celých čísel m a n
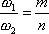 , , |
(4,214) |
vzniknou uzavřené křivky, které mají pro jednotlivé hodnoty
poměru
(4,214)
charakteristický tvar. Tyto křivky nazýváme Lissajousovými obrazci.
Na obr.35 jsou nakresleny Lissajousovy obrazce pro hodnoty poměru
(4,214)
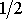 a
a
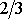 . Pro každý poměr je uvažováno několik hodnot rozdílu fázových konstant
. Pro každý poměr je uvažováno několik hodnot rozdílu fázových konstant
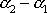 . Všimněme si, že poměr počtu míst, v kterých se na vzájemně kolmých
stranách Lissajousův obrazec dotýká opsaného obdélníka, odpovídá poměru
(4,214)
.
. Všimněme si, že poměr počtu míst, v kterých se na vzájemně kolmých
stranách Lissajousův obrazec dotýká opsaného obdélníka, odpovídá poměru
(4,214)
.