4.7 Energie harmonických kmitů

Vypočteme nejprve celkovou mechanickou energii 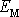hmotného bodu o hmotnosti m, který koná harmonický kmit (1,25) , tj. pro který výchylka

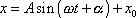.	(1,25)

Uvážíme-li, že rychlost pohybu (1,25) je 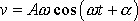, dostáváme pro kinetickou energii 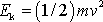hmotného bodu

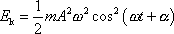.	(4,164)

Síla F působící harmonický pohyb (1,25) je rovna 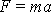, kde dle (1,33) , tedy

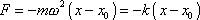.	(4,165)

V druhé části rovnice (4,165) jsme ve shodě s rovnicí (2,12) položili . Použijeme-li rovnici (3,13) k výpočtu potenciální energie hmotného bodu v místě x silového pole (4,165) , dostáváme

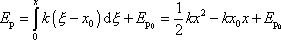Integrační proměnnou jsme označili , aby nedošlo k záměně s výchylkou x hmotného bodu. Položíme-li pro , dostáváme , odkud plyne 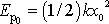, a tedy

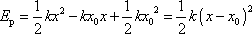.	(4,166)

Výsledek (4,166) lze též získat rychleji, položíme-li bod, vůči kterému potenciální energii počítáme do rovnovážné polohy 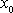kmitu (1,25) a potenciální energii v tomto bodě pokládáme za nulovou. Potom přímo

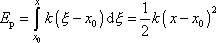.	(4,166)

Na obr.29 je znázorněna funkce (4,166) 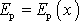, tj. závislost potenciální energie příslušné silovému poli (4,165) , v kterém hmotný bod koná harmonický kmit. Závislost je kvadratická, grafické znázornění je parabola s vrcholem v bodě , . Dosadíme-li do (4,166) za 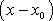z (1,25) ,

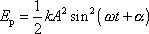.	(4,167)

Uvědomíme-li si, že 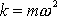a dosadí-me 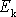dle (4,164) , dostáváme pro celkovou mechanickou energii hmotného bodu konajícího harmonický kmit vyjádření

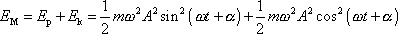Tedy

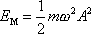.	(4,168)

Pohybuje-li se hmotný bod o známé hmotnosti m v silovém poli (4,165) se zadanou konstantou k, je rovnicí (2,12) určena frekvence 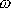jeho kmitu. Amplituda A kmitu je dána celkovou mechanickou energií hmotného bodu. (V případě, že by byla zvolena nenulová potenciální energie 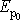v rovnovážné poloze kmitu, amplituda by byla určena rozdílem energií 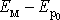.) Udáním potenciální energie silového pole a celkové mechanické energie hmotného bodu je určen harmonický kmit hmotného bodu až na fázovou konstantu 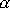, která těmito údaji určena není. Na obr.29 je znázorněna celková mechanick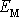á energie a jí odpovídající amplituda kmitů A. V okamžiku, kdy je celková energie rovna potenciální energii 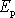, je kinetická energie, a tím i rychlost hmotného bodu nulová a hmotný bod zaujímá svou maximální výchylku amplitudu A.

Z výrazu (4,168) je zřejmé, že celková mechanická energie harmonického kmitu je konstantní na čase nezávislá veličina. Takovýto závěr nelze vyslovit pro celkovou mechanickou energii tlumeného harmonického kmitu

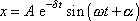.	(4,103)

Vypočteme úbytek celkové mechanické energie 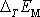hmotného bodu o hmotnosti m konajícího pohyb (4,103) za dobu kmitu T. Průchody hmotného bodu rovnovážnou polohou, které při vyjádření kmitu rovnicí (4,103) nastávají vždy, když 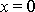, následují po sobě v časových intervalech 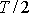. Srovnáme energii hmotného bodu ve dvou za čas T po sobě následujících průchodech rovnovážnou polohou. 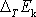Potenciální energie v rovnovážné poloze je vždy stejná (zpravidla ji pokládáme za nulovou) a rozdíl je dán rozdílem kinetických energií hmotného bodu v obou uvažovaných průchodech rovnovážnou polohou

.	(4,169)

Rychlost tlumeného harmonického kmitu je dána výrazem

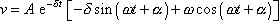.	(4,104)

V rovnovážné poloze je , a tedy dle (4,103) . Potom ovšem 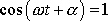a rychlost v rovnovážné poloze dle (4,104) je dána jednoduchým výrazem

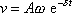(4,170)

a pro dostáváme vyjádření

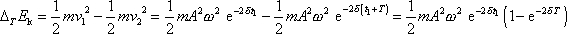.	(4,171)

V rovnici (4,171) je 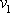rychlost při prvním průchodu rovnovážnou polohou v čase 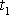a rychlost při druhém průchodu v čase 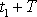; při vyjádření (4,171) pokládáme 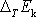za kladnou veličinu. Použijeme-li přibližného vyjádření (první dva členy Taylorova rozvoje)

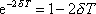,	(4,172)

které platí pro malé hodnoty 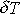, k úpravě pravé strany rovnice (4,171) a výsledek dosadíme do rovnice (4,169) , můžeme pro úbytek mechanické energie hmotného bodu během jednoho kmitu psát vyjádření

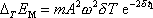.	(4,173)

Tento úbytek závisí na čase , kdy jej uvažujeme. Dle rovnice (3,11) přírůstek kinetické energie hmotného bodu 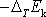je roven práci vnějších sil působících na hmotný bod. V uvažovaném případě práce elastické síly (4,68) 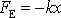během jednoho cyklu je nulová, a proto přírůstek kinetické energie musí být roven práci odporující disipativní síly (4,69) 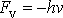, tedy

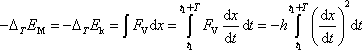.	(4,174)

O tom, že integrál dává výraz (4,171) se lze přesvědčit přímým výpočtem.

4.7.1 Činitel jakosti Q a energie kmitů

Pro charakteristiku kmitajících systémů, v kterých dochází k rozptylu (disipaci) energie, se užívá činitel jakosti Q, který se zavádí jako 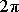násobek poměru průměrné energie 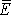kmitu k energii 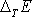rozptýlené při tomto kmitu, tedy

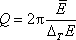.	(4,175)

Vypočteme přibližné vyjádření činitele jakosti Q pro tlumený harmonický kmit. Za průměrnou energii položíme hodnotu odpovídající výrazu (4,168) , kam za amplitudu kmitu v čase 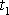dosadíme dle (4,103) výraz 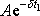, tedy

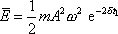.	(4,176)

Pro 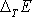(zde a dále v tomto článku vynecháme index M u celkové mechanické energie; tedy ) použijeme přibližné vyjádření (4,173) . Potom

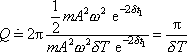a dosadíme-li dle (4,105) 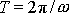, dostáváme pro činitel jakosti přibližné vyjádření

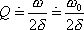(4,177)

platné pro slabě tlumené kmity.

Vypočteme energii rozptýlenou během jednoho cyklu u vynuceného harmonického kmitu

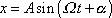(4,130)

v ustáleném stavu. V případě ustálených vynucených harmonických kmitů je energie rozptýlená vlivem odporující disipativní síly (4,69) 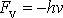doplněna prací vykonanou na hmotný bod vynucující silou (4,121) 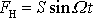. Celková energie hmotného bodu konajícího kmit (4,130) zůstává tak zachována. Energii 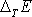rozptýlenou během jednoho kmitu vypočteme jednak jako záporně vzatou práci vykonanou silou 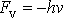, tedy dle rovnice (4,174) ,

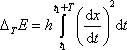,	(4,178)

jednak jako práci vykonanou na hmotný bod během jednoho cyklu silou 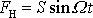, tj.

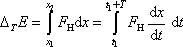.	(4,179)

Derivace kmitu (4,130) je 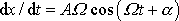a jelikož 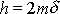(viz text k rovnici (4,71) ), dostáváme z rovnice (4,178)

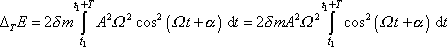a protož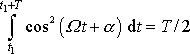e , je

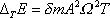.	(4,180)

Průměrný výkon 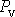rozptylující síly je, uvědomíme-li si, že výraz jsme počítali pro záporně vzatou sílu ,

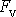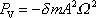.	(4,181)

Vypočteme-li 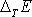z rovnice (4,179) , dostáváme

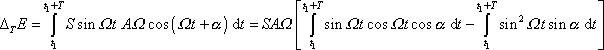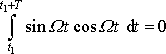Protože a , je

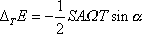.	(4,182)

Jelikož 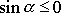(viz obr.27) a ostatní veličiny v (4,182) jsou kladné, je 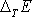dané rovnicí (4,182) nezáporné. Pro průměrný výkon 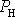vynucující síly dostáváme z (4,182)

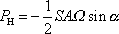.	(4,183)

Použijeme-li trigonometrického vztahu 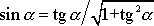a pro 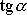vyjádření (4,127) , je

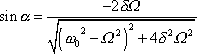(4,184)

a vyjádříme-li amplitudu kmitu A dle (4,128) , můžeme po dosazení do (4,183) pro napsat

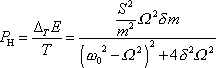.	(4,185)

Dosadíme-li stejné vyjádření (4,128) amplitudy kmitu A do výrazu (4,181) pro výkon dostáváme

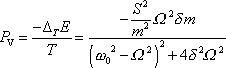.	(4,186)

Tedy, jak jsme již výše kvalitativně naznačili, výkon vynucující síly a odporující síly je stejně velký ale opačného znaménka.

Vyšetříme závislost výkonu 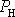na frekvenci kmitů W. Přihlédneme-li k rovnici 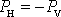a porovnáme výraz (4,181) s výrazem (4,168) pro energii kmitů 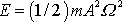, vidíme, že tvar závislosti a 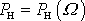bude stejný. Funkce 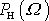daná rovnicí (4,185) je nulová pro a pro 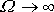. Položíme-li derivaci funkce rovnu nule, zjistíme, že další extrém nastane pro 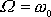. Vzhledem k tomu, že funkce (4,185) je vždy kladná, je tento extrém maximem. Pro 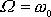nastane maximum funkce 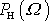, a tedy též maximum funkce 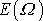. Funkce 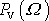, jelikož , má pro 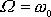minimum. 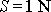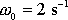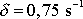Křivky a pro , , a 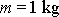jsou znázorněny na obr.30. Nazývají se rezonančními křivkami absorbovaného výkonu a energie. Rezonance celkové mechanické energie kmitajícího hmot-ného bodu a absorbovaného výkonu nastává nezávisle na velikosti tlumení přesně, když

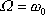(4,187)

na rozdíl od rezonance výchylky, která nastává při

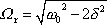.	(4,135)

Činitel jakosti kmitajícího systému, který koná vynucený harmonický kmit, nelze počítat dle vztahu (4,175) při libovolné frekvenci. Výsledek, který jakožto cha-rakteristika kmitajícího systému má být shodný s (4,177) , dostaneme pouze, když frekvence vynuceného kmitu je shodná s vlastní frekvencí 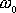systému, tedy při rezonanci energie (4,187) . Dosadíme-li dle (4,168) za průměrnou energii kmitu (4,130)

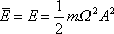a za energii rozptýlenou během jednoho kmitu výraz (4,180) , výraz (4,175) pro zavedení činitele jakosti dává

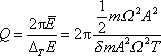Zkrátíme-li poslední výraz a dosadíme za dobu kmitu T při rezonanci výraz 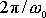, dostaneme pro činitel jakosti vyjádření

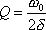.	(4,188)

Dostali jsme tak rovnici (4,177) jako přesnou rovnici, odvozenou bez jakýchkoli zanedbání. U vynucených kmitů je energie rozptýlená během jednoho cyklu hned doplněna vnější vynucující silou, hmotný bod koná čistý harmonický kmit a výpočet Q je formálně jednodušší než u tlumených kmitů.

Celkovou energii E kmitu při rezonanci můžeme dle (4,175) psát jako

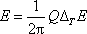,	(4,189)

uvědomíme-li si, že u vynucených kmitů 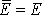. Celková energie E kmitu je dle (4,189) při velké hodnotě Q, která je u řady kmitajících systémů běžná, podstatně větší než energie 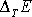dodávaná kmitu během jednoho cyklu. Velkou celkovou energii získá kmit postupně v přechodové době, kdy kmitání se dostává do ustáleného stavu. Možnost udržovat vysokou energii E systému kmitajícího v rezonanci malou dodávanou energií 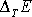je často technicky využívána. Provedená úvaha nám objasňuje, proč veličina Q se nazývá činitelem jakosti kmitajícího systému.

Kmitající systém se stejnou vlastní frekvencí a menším tlumením má užší rezonanční křivku a vyšší činitel jakosti. Ukážeme, jaký vztah platí mezi šířkou rezonanční křivky absorbovaného výkonu (obr.30) v její poloviční výšce a činitelem jakosti Q. Při rezonanci, když 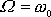, je dle (4,185)

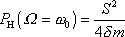Poloviční hodnoty nabude funkce 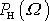pro frekvence splňující podmínku

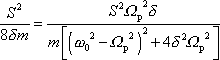kterou můžeme dále upravovat

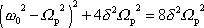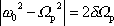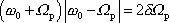Užijeme přibližného vyjádření 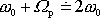platného pro nepříliš široké rezonanční křivky a 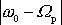označíme . Poslední rovnici potom můžeme přepsat na tvar

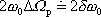neboli

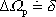a pro činitel jakosti daný rovnicí (4,188) potom dostáváme

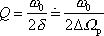.	(4,190)

Výraz je šířka rezonanční křivky 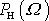v její poloviční výšce, jak je znázorněno na obr.31. Na témž obrázku jsou také naznačeny obě frekvence 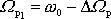a 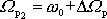, pro které je splněna rovnice . Známe-li šířku rezonanční křivky 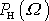v poloviční výšce, lze dle rovnice (4,190) přímo stanovit činitel jakosti kmitajícího systému a zřejmě platí výše zmíněná nepřímá úměrnost mezi šířkou rezonanční křivky a činitelem jakosti.

Povšimneme si ještě jednoho významu činitele jakosti Q. Udává poměr amplitudy 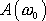vynuceného harmonického kmitu při rezonanci energie (a tedy též absorbovaného výkonu), tj. amplitudy při frekvenci 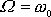, k statické výchylce (amplitudě) dané rovnicí (4,131) . Pro amplitudu 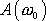dle (4,128) máme a statická amplituda dle (4,131) 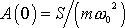, tedy

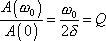.	(4,191)