 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Mějme dva hmotné body o stejné hmotnosti m, na které působí elastické síly úměrné výchylce bodu z rovnovážné polohy. Pohybová rovnice každého z hmotných bodů má tvar (2,10)
 , |
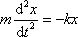(2,10) |
kde k
je kladná konstanta. Jak plyne řešením rovnice
(2,10)
, každý
z hmotných bodů koná harmonický kmit s frekvencí
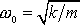. Systém, pro který platí rovnice
(2,10)
, bývá nazýván
harmonickým oscilátorem.
Budeme nyní sledovat, jak bude ovlivněn pohyb každého
z hmotných bodů každého harmonického oscilátoru , necháme-li mezi nimi
působit sílu úměrnou rozdílu mezi skutečnou vzdáleností a vzdáleností
rovnovážných poloh obou hmotných bodů. Smysl síly bude takový, aby se snažila
udržet rovnovážnou vzdálenost bodů. Popsanou sílu budeme nazývat pružnou
vazbou. Označíme souřadnici prvého hmotného bodu
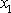, jeho rovnovážná poloha nastane pro
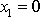a souřadnici druhého hmotného bodu
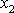, rovnovážná poloha tohoto hmotného bodu nastane pro
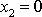. Vazbovou sílu
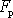, kterou působí prvý bod na druhý, lze pomocí těchto souřadnic zapsat ve tvaru
 , |
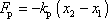(4,215) |
předpokládáme-li, že výchylky oscilátorů s nesouhlasným
znaménkem zvětšují odchylku vzdálenosti hmotných bodů od jejich rovnovážné
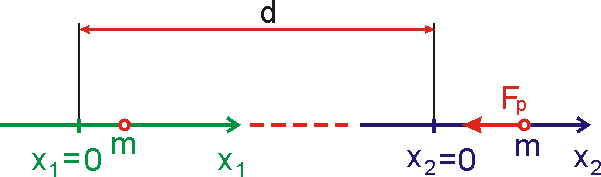
vzdálenosti. Příklad takového uspořádání je na obr.36, na kterém písmenem d
je označena rovnovážná vzdálenost. Konstanta
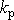v rovnici
(4,215)
je kladná. Pohybová
rovnice druhého hmotného bodu v přítomnosti síly
(4,215)
má tvar
 . |
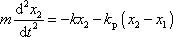(4,216) |
Uvědomíme-li si, že dle principu akce a reakce na první hmotný bod působí síla
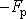, můžeme napsat jeho pohybovou rovnici
 . |
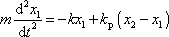(4,217) |
Rovnice
(4,216)
a
(4,217)
tvoří soustavu dvou
diferenciálních rovnic pro dvě neznámé funkce
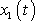a
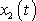. Jejich sečtením dostáváme rovnici
 |
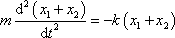(4,218) |
a odečtením rovnici
 , |
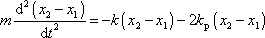(4,219) |
což jsou již samostatné diferenciální rovnice pro neznámé funkce
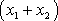a
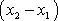. Obě rovnice mají tvar rovnice
(2,10)
pro harmonické kmity, první
s konstantou k a druhá s konstantou
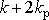. Z rovnice
(4,218)
tedy pro funkci
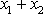plyne vyjádření
 , |
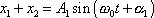(4,220) |
kde
 . |
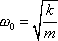(4,221) |
Řešení rovnice
(4,219)
dává pro funkci
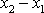vyjádření
 , |
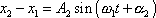(4,222) |
kde
 . |
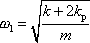(4,223) |
Sečtením a odečtením rovnic (4,220) a (4,222) získáme hledané funkce
 |
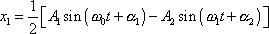(4,224) |
a
 |
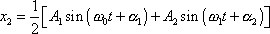(4,225) |
udávající pohyb jednotlivých hmotných bodů oscilátorů
vázaných pružnou vazbou
(4,215)
. Funkce
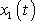a
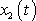jsou tvořeny algebraickým sečtením dvou harmonických kmitů, jednoho s původní frekvencí
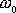volných kmitů a druhého s frekvencí
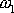, jejíž velikost, jak plyne z rovnice
(4,223)
, závisí na konstantě
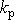, tj. na velikosti vazby. Přítomnost nové frekvence způsobené vazbou je
charakteristická pro vázané oscilátory.
V systémech, kde předpokládáme vazbu mnoha oscilátorů,
tj. např. v systémech, jimiž v teorii pevných látek (viz např.
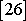) modelujeme chování krystalových mříží, je
vazeb mnoho, a tím i mnoho vibračních frekvencí. Právě probraný systém
dvou vázaných oscilátorů jakožto nejelementárnější model vázaných oscilačních
systémů nám pomůže později pochopit i tyto složitější modely. Kmity vázaných
oscilátorů složíme z dvou základních kmitů, tzv. vlastních kmitů
(oscilačních módů) systému. Ve složitějších systémech je oscilačních módů více,
rozklad kmitů do těchto módů je složitější, ale princip postupu zůstává
zachován.
Funkce
(4,224)
a
(4,225)
jsou funkce vzniklé složením dvou
harmonických kmitů. Je-li vazba slabá, tj.
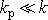, jsou frekvence
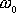a
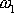blízké a funkce
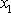a
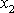mají (s výjimkou speciálně volených
počátečních podmínek pohybu) stejný tvar jako funkce, s níž jsme se
setkali při vyšetřování rázů, a která je znázorněna na obr.32. Některé způsoby
realizace vázaných kmitů a konkrétní tvar funkcí
(4,224)
a
(4,225)
pro
speciálně volené počáteční podmínky jsou ukázány v knize [17]
počínaje str. 148.
V předchozích částech jsme probrali řadu definic jednotlivých veličin mechaniky a vztahů mezi nimi. Skutečného porozumění však můžeme dosáhnout až vyřešíme řady konkrétních problémů. My se soustředíme pouze na několik základních:
4.1 Pohyb v gravitačním poliČtenáři doporučujeme, aby si jednotlivé příklady procházel v uvedeném pořadí, protože vysledky předchozích jsou často aplikovány v následujících.
|
|
|
|
|
|
|
|
|