Budeme nyní vyšetřovat případ, kdy na hmotný bod vázaný na
přímku působí vedle elastické síly
(4,68)
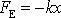 a odporující síly
(4,69)
a odporující síly
(4,69)
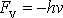 ještě další síla
ještě další síla
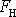 , jejíž časový průběh je dán harmonickou funkcí
, jejíž časový průběh je dán harmonickou funkcí
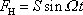 . . |
(4,121) |
Pohybová rovnice hmotného bodu o hmotnosti m je potom
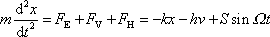 , , |
což je lineární diferenciální rovnice s konstantními koeficienty a s nenulovou pravou stranou, kterou můžeme zapsat v tvaru
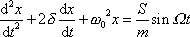 . . |
(4,122) |
V rovnici
(4,122)
jsme stejně jako v rovnici
(4,71)
užili označení
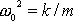 a
a
 . Podle výkladu z konce minulého článku je obecným řešením rovnice
(4,122)
. Podle výkladu z konce minulého článku je obecným řešením rovnice
(4,122)
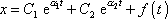 , , |
(4,123) |
kde
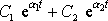 je řešení rovnice
(4,122)
bez pravé strany, tedy řešení rovnice
(4,71)
a
je řešení rovnice
(4,122)
bez pravé strany, tedy řešení rovnice
(4,71)
a
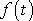 je jedno řešení celé rovnice
(4,122)
.
je jedno řešení celé rovnice
(4,122)
.
Je-li na pravé straně rovnice
(4,122)
harmonická funkce s frekvencí
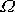 , je řešení
, je řešení
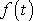 dáno harmonickou funkcí se stejnou frekvencí
dáno harmonickou funkcí se stejnou frekvencí
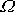 , jak ukážeme přímým výpočtem. Budeme předpokládat, že
, jak ukážeme přímým výpočtem. Budeme předpokládat, že
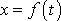 , kde
, kde
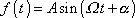 . . |
(4,124) |
Dosadíme-li funkci
 spolu s její první a druhou derivaci do rovnice
(4,122)
, dostáváme rovnici
spolu s její první a druhou derivaci do rovnice
(4,122)
, dostáváme rovnici
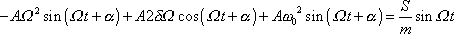 , , |
kterou, užijeme-li vzorce
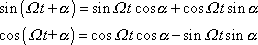 , , |
můžeme po úpravě přepsat na tvar
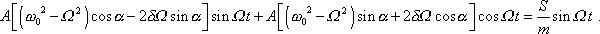 |
(4,125) |
Má-li funkce
 být řešením rovnice
(4,122)
pro všechna t,
musí rovnice
(4,125)
být splněna pro všechna t. Jelikož funkce
být řešením rovnice
(4,122)
pro všechna t,
musí rovnice
(4,125)
být splněna pro všechna t. Jelikož funkce
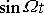 a
a
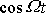 jsou lineárně nezávislé, lze rovnici
(4,125)
splnit pro všechna t pouze tehdy, když se budou rovnat číselné koeficienty u
jsou lineárně nezávislé, lze rovnici
(4,125)
splnit pro všechna t pouze tehdy, když se budou rovnat číselné koeficienty u
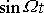 a
a
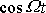 na obou stranách rovnice
(4,125)
. Tak dostáváme rovnice
na obou stranách rovnice
(4,125)
. Tak dostáváme rovnice
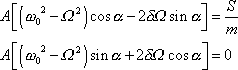 . . |
(4,126) |
Z druhé rovnice
(4,126)
dostáváme, předpokládáme-li
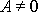 , pro dosud neurčenou fázovou konstantu
, pro dosud neurčenou fázovou konstantu
 podmínku
podmínku
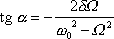 . . |
(4,127) |
Umocníme-li obě rovnice systému (4,126) na druhou a sečteme je, dostaneme po úpravě pro amplitudu A vyjádření
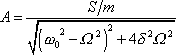 . . |
(4,128) |
S hodnotami A,
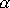 danými rovnicemi
(4,128)
a
(4,127)
lze splnit
rovnice
(4,126)
, a tedy i rovnici
(4,125)
pro všechna t. Funkce
danými rovnicemi
(4,128)
a
(4,127)
lze splnit
rovnice
(4,126)
, a tedy i rovnici
(4,125)
pro všechna t. Funkce
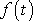 s amplitudou A
danou rovnicí
(4,128)
a fázovou konstantou
určenou rovnicí
(4,127)
je tedy hledaným jedním řešením celé (tj. včetně pravé
strany) rovnice
(4,122)
. Obecné řešení rovnice
(4,122)
dostaneme dosazením
s amplitudou A
danou rovnicí
(4,128)
a fázovou konstantou
určenou rovnicí
(4,127)
je tedy hledaným jedním řešením celé (tj. včetně pravé
strany) rovnice
(4,122)
. Obecné řešení rovnice
(4,122)
dostaneme dosazením
 do jeho vyjádření
(4,123)
do jeho vyjádření
(4,123)
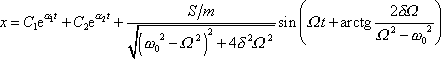 . . |
(4,129) |
Část řešení
(4,129)
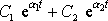 , která je řešením rovnice
(4,71)
, jsme podrobně rozebrali v předcházejícím
článku. Tam jsme ukázali, že tato část řešení konverguje k nule
s rostoucím časem t
(viz rovnici
(4,83)
). Po dostatečně dlouhé době, neboli jak říkáme
v ustáleném stavu, lze zanedbat vliv výrazu
, která je řešením rovnice
(4,71)
, jsme podrobně rozebrali v předcházejícím
článku. Tam jsme ukázali, že tato část řešení konverguje k nule
s rostoucím časem t
(viz rovnici
(4,83)
). Po dostatečně dlouhé době, neboli jak říkáme
v ustáleném stavu, lze zanedbat vliv výrazu
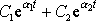 na řešení
(4,129)
a za řešení v ustáleném stavu pokládat pouze funkci
na řešení
(4,129)
a za řešení v ustáleném stavu pokládat pouze funkci
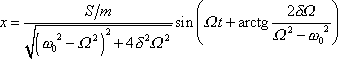 . . |
(4,130) |
Zajímá-li nás pohyb hmotného bodu bezprostředně po aplikaci
síly
(4,121)
, musíme znát jeho stav, tj. nejlépe jeho polohu a rychlost
v okamžiku, kdy síla
(4,121)
bude aplikována. Z těchto počátečních
podmínek můžeme pak určit konstanty
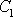 a
a
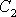 a získat obecné řešení
(4,129)
rovnice
(4,122)
. Najdeme-li takové řešení, které zřejmě pro
a získat obecné řešení
(4,129)
rovnice
(4,122)
. Najdeme-li takové řešení, které zřejmě pro
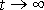 přechází v řešení
(4,130)
, říkáme, že
jsme nalezli řešení v přechodovém stavu. Dále se omezíme na vyšetřování
pohybu hmotného bodu v ustáleném stavu.
přechází v řešení
(4,130)
, říkáme, že
jsme nalezli řešení v přechodovém stavu. Dále se omezíme na vyšetřování
pohybu hmotného bodu v ustáleném stavu.
Amplituda A
(4,128)
ustáleného řešení
(4,130)
rovnice
(4,122)
je přímo úměrná výrazu
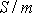 , tj. amplitudě S vynucující síly
(4,121)
připadající na jednotku hmotnosti pohybujícího se hmotného bodu. Budeme-li dále
pokládat veličiny
, tj. amplitudě S vynucující síly
(4,121)
připadající na jednotku hmotnosti pohybujícího se hmotného bodu. Budeme-li dále
pokládat veličiny
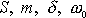 za konstanty, zjistíme, že amplituda A
podstatným způsobem závisí na frekvenci W.
Již zběžný pohled na rovnici
(4,128)
ukazuje, že při W blízkém
za konstanty, zjistíme, že amplituda A
podstatným způsobem závisí na frekvenci W.
Již zběžný pohled na rovnici
(4,128)
ukazuje, že při W blízkém
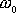 , a při malé hodnotě útlumové konstanty
, a při malé hodnotě útlumové konstanty
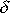 veličina A
může nabývat značných hodnot. Jev, kdy malá budící veličina
způsobí velkou odezvu jiné veličiny, nazýváme rezonancí.
Ve zde uvažovaném případě se jedná o rezonanci výchylky
(4,130)
způsobené budící silou
(4,121)
. Rozebereme závislost amplitudy A
na frekvenci W danou rovnicí
(4,128)
podrobněji
veličina A
může nabývat značných hodnot. Jev, kdy malá budící veličina
způsobí velkou odezvu jiné veličiny, nazýváme rezonancí.
Ve zde uvažovaném případě se jedná o rezonanci výchylky
(4,130)
způsobené budící silou
(4,121)
. Rozebereme závislost amplitudy A
na frekvenci W danou rovnicí
(4,128)
podrobněji
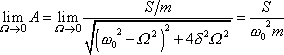 . . |
(4,131) |
Hodnota
 , ke které se blíží amplituda A pro malé hodnoty budicí frekvence W,
je rovna výchylce hmotného bodu z rovnovážné polohy, když na něj působí síla S
stálé velikosti a elastická síla
(4,68)
, ke které se blíží amplituda A pro malé hodnoty budicí frekvence W,
je rovna výchylce hmotného bodu z rovnovážné polohy, když na něj působí síla S
stálé velikosti a elastická síla
(4,68)
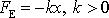 . Výrazu
(4,131)
budeme říkat statická výchylka. Extrém funkce
. Výrazu
(4,131)
budeme říkat statická výchylka. Extrém funkce
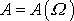 nastane, když
nastane, když
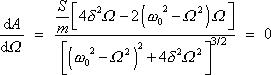 . . |
(4,132) |
Uvažujeme-li podle povahy veličiny pouze
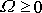 , je podmínka
(4,132)
splněna pro
, je podmínka
(4,132)
splněna pro
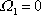 , , |
(4,133) |
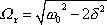 |
(4,134) |
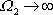 . . |
(4,135) |
Frekvencím
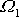 a
a
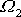 odpovídá extrémní hodnota vždy. Extrém funkce
odpovídá extrémní hodnota vždy. Extrém funkce
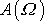 pro hodnotu
pro hodnotu
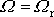 nastane pouze tehdy, je-li hodnota
nastane pouze tehdy, je-li hodnota
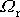 reálná, tedy, je-li splněna podmínka
reálná, tedy, je-li splněna podmínka
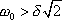 . . |
(4,136) |
Hodnota
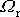 je reálná i pro
je reálná i pro
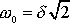 , ale v tom případě
, ale v tom případě
 a splývá s
a splývá s
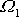 .
.
Srovnáme velikosti
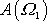 a
a
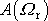 . Výraz pod odmocninou ve jmenovateli výrazu
(4,128)
je pro
. Výraz pod odmocninou ve jmenovateli výrazu
(4,128)
je pro
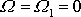 roven
roven
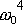 a v případě
a v případě
 jej lze upravit následujícím způsobem
jej lze upravit následujícím způsobem
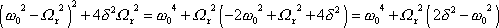 . . |
Je-li splněna podmínka
(4,136)
je
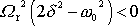 a
a
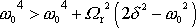 . Kladný jmenovatel výrazu
. Kladný jmenovatel výrazu
 je větší než jmenovatel výrazu
je větší než jmenovatel výrazu
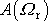 , a tedy
, a tedy
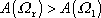 . . |
(4,137) |
Z rovnice (4,128) plyne
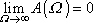 . . |
(4,138) |
Při splnění podmínky
(4,136)
,
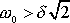 , je extrém funkce
, je extrém funkce
 při hodnotě
při hodnotě
 maximem. Říkáme, že pro
maximem. Říkáme, že pro
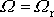 nastává rezonance výchylky a frekvenci
nastává rezonance výchylky a frekvenci
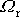 říkáme rezonanční frekvence. Velikost rezonanční amplitudy je větší než statická výchylka
(4,131)
.
říkáme rezonanční frekvence. Velikost rezonanční amplitudy je větší než statická výchylka
(4,131)
.
V případě
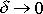 , a tedy též dle
(4,134)
, a tedy též dle
(4,134)
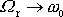 , plyne z rovnice
(4,128)
, plyne z rovnice
(4,128)
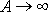 . Při malých hodnotách
. Při malých hodnotách
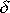 rezonanční amplituda
rezonanční amplituda
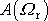 značně převyšuje statickou výchylku
(4,131)
a v dobrém přiblížení platí často uvažovaný vztah, že rezonance nastává,
když frekvence vynucující síly
značně převyšuje statickou výchylku
(4,131)
a v dobrém přiblížení platí často uvažovaný vztah, že rezonance nastává,
když frekvence vynucující síly
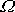 je rovna frekvenci
je rovna frekvenci
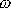 (definice
(4,99)
) vlastních kmitů soustavy,
a tedy i frekvenci
(definice
(4,99)
) vlastních kmitů soustavy,
a tedy i frekvenci
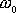 netlumených kmitů. Pro malá
netlumených kmitů. Pro malá
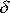 platí přibližné rovnice
platí přibližné rovnice
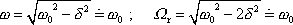 , , |
a tedy
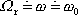 . . |
(4,139) |
Při přesném výpočtu je si však nutno uvědomit, že dle (4,134)
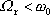 , , |
(4,140) |
tedy rezonanční frekvence je poněkud nižší než frekvence odpovídajících netlumených kmitů.
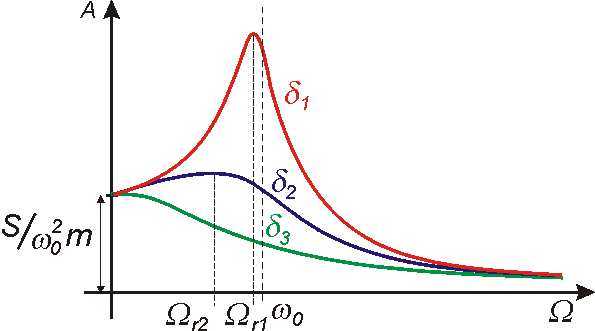 Po provedené analýze můžeme zakreslit funkci
Po provedené analýze můžeme zakreslit funkci
 pro případ, kdy je splněna podmínka
(4,136)
pro případ, kdy je splněna podmínka
(4,136)
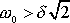 , která je ostřejší než podmínka
, která je ostřejší než podmínka
 uvedená v minulém článku jako podmínka pro vznik tlumených kmitů. Křivka
uvedená v minulém článku jako podmínka pro vznik tlumených kmitů. Křivka
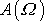 má tvar znázorněný pro dvě hodnoty tlumící konstanty
má tvar znázorněný pro dvě hodnoty tlumící konstanty
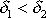 na obr.26. Tyto křivky se nazývají rezonančními křivkami výchylky (amplitudy).
Je-li splněna podmínka
(4,136)
, má funkce
na obr.26. Tyto křivky se nazývají rezonančními křivkami výchylky (amplitudy).
Je-li splněna podmínka
(4,136)
, má funkce
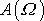 pro
pro
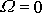 lokální minimum. Není-li splněna podmínka
(4,136)
, má funkce
lokální minimum. Není-li splněna podmínka
(4,136)
, má funkce
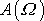 pro
pro
 maximum, jak je znázorněno na obr.26 křivkou označenou
maximum, jak je znázorněno na obr.26 křivkou označenou
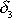 (
(
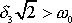 ).
).
Budeme nyní sledovat, jak závisí fázová konstanta
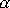 stanovená rovnicí
stanovená rovnicí
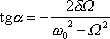 |
(4,103) |
na frekvenci
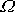 při konstant-ních hodnotách
při konstant-ních hodnotách
 a
a
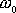 . Pro
. Pro
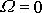 plyne z rovnice
(4,127)
plyne z rovnice
(4,127)
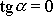 , a tedy
, a tedy
 , kde
, kde
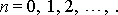 Přihlédneme-li k rovnicím
(4,126)
,
z kterých byla rovnice
(4,127)
odvozena, zjistíme, že lichá n
v rovnici
Přihlédneme-li k rovnicím
(4,126)
,
z kterých byla rovnice
(4,127)
odvozena, zjistíme, že lichá n
v rovnici
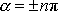 musíme vypustit, protože první z rovnic
(4,126)
by pro ně přiřazovala kladnému S
záporné A, což neodpovídá pojetí amplitudy jako kladné veličiny.
Hodnota
musíme vypustit, protože první z rovnic
(4,126)
by pro ně přiřazovala kladnému S
záporné A, což neodpovídá pojetí amplitudy jako kladné veličiny.
Hodnota
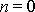 a sudé hodnoty n odpovídají fyzikálně stejnému případu
a sudé hodnoty n odpovídají fyzikálně stejnému případu
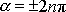 , kdy výchylka
, kdy výchylka
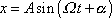 |
(4,130) |
a síla
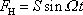 |
(4,121) |
jsou ve fázi. V dalším se omezíme na případ
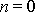 , tedy pro
, tedy pro
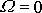 , položíme
, položíme
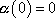 . . |
(4,141) |
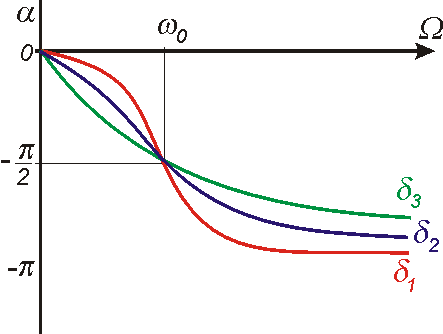 Pro frekvenci
Pro frekvenci
 z oboru
z oboru
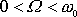 je dle
(4,127)
je dle
(4,127)
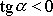 , a tedy vzhledem k volbě
(4,141)
fázová konstanta
, a tedy vzhledem k volbě
(4,141)
fázová konstanta
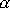 v intervalu
v intervalu
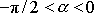 . V tomto oboru leží, je-li splněna podmínka
(4,136)
i rezonanční
frekvence
. V tomto oboru leží, je-li splněna podmínka
(4,136)
i rezonanční
frekvence
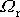 , pro kterou dosazením
(4,134)
do
(4,127)
zjistíme, že
, pro kterou dosazením
(4,134)
do
(4,127)
zjistíme, že
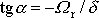 , tedy
, tedy
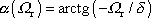 . . |
(4,142) |
Pro
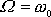 plyne z
(4,127)
plyne z
(4,127)
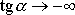 , tedy
, tedy
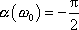 . . |
(4,143) |
Pro výraz
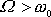 je výraz
(4,127)
kladný. Uvážíme-li volbu
oboru (viz
(4,141)
) fázové konstanty
je výraz
(4,127)
kladný. Uvážíme-li volbu
oboru (viz
(4,141)
) fázové konstanty
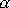 , musíme hodnotám
, musíme hodnotám
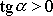 přiřadit
přiřadit
 z intervalu
z intervalu
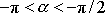 . Pro
. Pro
 je
je
 , a tedy
, a tedy
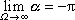 . . |
(4,144) |
Průběh funkce
 je pro tři různé hodnoty tlumicí konstanty
je pro tři různé hodnoty tlumicí konstanty
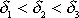 znázorněn na obr. 27.
znázorněn na obr. 27.
Popíšeme kvalitativně výsledky získané při sledování vztahu mezi vynucující silou
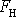 (4,121)
a vynuceným kmitem v ustáleném stavu
(4,130)
, je-li tlumení
(4,121)
a vynuceným kmitem v ustáleném stavu
(4,130)
, je-li tlumení
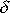 malé. Při malých frekvencích
malé. Při malých frekvencích
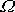 vynucující síly ve srovnání s frekvencí
vynucující síly ve srovnání s frekvencí
 hmotný bod se pohybuje přibližně ve fázi
s vynucující silou a amplituda jeho kmitů je blízká statické výchylce
(4,131)
. Lze říci, že elastická síla
(4,68)
je rozhodující pro průběh pohybu
v tomto oboru frekvencí. V oblasti rezonance, tj. pro frekvence
hmotný bod se pohybuje přibližně ve fázi
s vynucující silou a amplituda jeho kmitů je blízká statické výchylce
(4,131)
. Lze říci, že elastická síla
(4,68)
je rozhodující pro průběh pohybu
v tomto oboru frekvencí. V oblasti rezonance, tj. pro frekvence
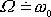 , se výchylka fázově zpožďuje o
, se výchylka fázově zpožďuje o
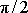 za budicí silou
za budicí silou
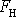 . Budicí síla
. Budicí síla
 je přibližně ve fázi s rychlostí pohybu
hmotného bodu a urychluje jej v nejvhodnější fázi pohybu. Tím lze
vysvětlit velké hodnoty amplitudy kmitu při rezonanci. Je-li frekvence
je přibližně ve fázi s rychlostí pohybu
hmotného bodu a urychluje jej v nejvhodnější fázi pohybu. Tím lze
vysvětlit velké hodnoty amplitudy kmitu při rezonanci. Je-li frekvence
 vysoká ve srovnání s frekvencí
vysoká ve srovnání s frekvencí
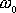 , fázové zpoždění výchylky za budicí silou se blíží
, fázové zpoždění výchylky za budicí silou se blíží
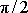 a amplituda kmitů klesá k nule. Velikost zrychlení harmonického kmitu je dle
(1,32)
úměrná
a amplituda kmitů klesá k nule. Velikost zrychlení harmonického kmitu je dle
(1,32)
úměrná
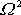 a amplitudě kmitu. Vynucující síla, jejíž amplitudu S
pokládáme za frekvenčně
nezávislou, je schopna realizovat jen omezené hodnoty zrychlení hmotného bodu o
nenulové hmotnosti m. Klesání amplitudy A
vynucených kmitů se vzrůstající frekvencí k nule, je takto zcela
pochopitelné.
a amplitudě kmitu. Vynucující síla, jejíž amplitudu S
pokládáme za frekvenčně
nezávislou, je schopna realizovat jen omezené hodnoty zrychlení hmotného bodu o
nenulové hmotnosti m. Klesání amplitudy A
vynucených kmitů se vzrůstající frekvencí k nule, je takto zcela
pochopitelné.
Při rezonanci je fázové posunutí mezi vynucující silou
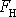 a ustálenou výchylkou x blízké
a ustálenou výchylkou x blízké
 . Když síla je maximální, výchylka je minimální a jejich součin udávající práci
dodanou systému je malý. K udržení velkých rezonančních výchylek
v ustáleném stavu stačí, aby vynucující síla dodávala jen minimální práci
(úměrnou odchylce fázového posunutí od
. Když síla je maximální, výchylka je minimální a jejich součin udávající práci
dodanou systému je malý. K udržení velkých rezonančních výchylek
v ustáleném stavu stačí, aby vynucující síla dodávala jen minimální práci
(úměrnou odchylce fázového posunutí od
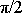 ) na kompenzování ztrát systému. Velké rezonanční
výchylky vznikají postupnou akumulací práce dodané systému v přechodovém
stavu, kdy se rezonance ustaluje.
) na kompenzování ztrát systému. Velké rezonanční
výchylky vznikají postupnou akumulací práce dodané systému v přechodovém
stavu, kdy se rezonance ustaluje.
Řešení rovnice
(4,122)
v ustáleném stavu lze nalézt
rychleji, užijeme-li reprezentace kmitů komplexními čísly. Harmonický kmit
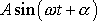 lze reprezentovat komplexním číslem
lze reprezentovat komplexním číslem
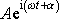 , stručně zapíšeme
, stručně zapíšeme
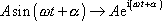 . . |
(4,145) |
Komplexní číslo
 má reálnou i imaginární část rovnu
harmonickému kmitu
má reálnou i imaginární část rovnu
harmonickému kmitu
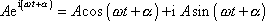 . . |
(4,146) |
V reprezentaci
(4,145)
můžeme pravou stranu rovnice
(4,122)
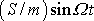 nahradit komplexním číslem
nahradit komplexním číslem
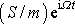 ,
,
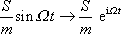 . . |
(4,147) |
Ustálené řešení rovnice
(4,122)
, které jsme hledali v tvaru
(4,124)
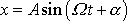 , budeme v komplexní reprezentaci hledat v tvaru
, budeme v komplexní reprezentaci hledat v tvaru
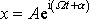 ;
;
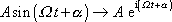 . . |
(4,148) |
Dosadíme-li komplexní výrazy spolu s jejich derivacemi
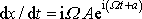 a
a
 do rovnice
(4,122)
, dostaneme místo rovnice
(4,125)
rovnici
do rovnice
(4,122)
, dostaneme místo rovnice
(4,125)
rovnici
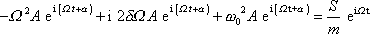 . . |
Ta po vydělení výrazem
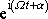 a vytknutí A přejde na tvar
a vytknutí A přejde na tvar
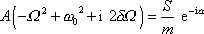 . . |
(4,149) |
Komplexní číslo v závorce na levé straně rovnice
(4,149)
označíme
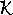 , tedy
, tedy
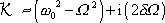 |
(4,150) |
a užijeme-li zápisu komplexního čísla
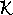 v tvaru
v tvaru
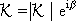 , , |
(4,151) |
kde
 |
(4,152) |
a
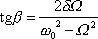 , , |
(4,153) |
můžeme rovnici (4,149) přepsat na tvar
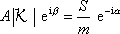 . . |
(4,154) |
Z rovnice
(4,154)
, jelikož A,
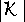 a S/m jsou reálná čísla, plyne
a S/m jsou reálná čísla, plyne
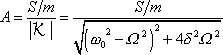 |
(4,155) |
a
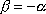 , , |
odkud
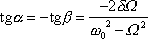 . . |
(4,156) |
Rovnice
(4,156)
je shodná s rovnicí
(4,127)
a rovnice
(4,155)
s rovnicí
(4,128)
. Tyto rovnice udávají, vrátíme-li se
v reprezentaci
(4,148)
zpět k reálné funkci
 , hledané hodnoty A a
, hledané hodnoty A a
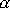 . Uvědomíme-li si, že rovnice
(4,150)
a
(4,154)
jsou elementární rovnice algebry
komplexních čísel, je nalezení hodnot A a
. Uvědomíme-li si, že rovnice
(4,150)
a
(4,154)
jsou elementární rovnice algebry
komplexních čísel, je nalezení hodnot A a
 při užití komplexní reprezentace snazší, než
při výše uvedeném přímém postupu.
při užití komplexní reprezentace snazší, než
při výše uvedeném přímém postupu.
Ustálené řešení rovnice
(4,122)
přiřazuje harmonickému kmitu
na pravé straně rovnice harmonický kmit téže frekvence, ale jiné amplitudy a
jiné fáze. Vidíme, že při výše prováděných reprezentacích nebyl výraz
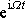 pro hledané řešení podstatný. Máme-li
rovnici typu rovnice
(4,122)
s pravou stranou rovnou harmonické funkci
pro hledané řešení podstatný. Máme-li
rovnici typu rovnice
(4,122)
s pravou stranou rovnou harmonické funkci
 , tj. rovnici
, tj. rovnici
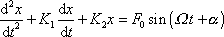 , , |
(4,122´) |
můžeme parametry jejího ustáleného řešení hledat tak, že jak funkci
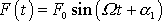 tak i ustálenému řešení známého tvaru
tak i ustálenému řešení známého tvaru
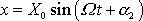 přiřadíme neproměnná komplexní čísla
přiřadíme neproměnná komplexní čísla
 a
a
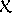 . Přiřazení provedem následujícím způsobem:
. Přiřazení provedem následujícím způsobem:
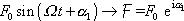 , , |
(4,157) |
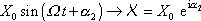 . . |
(4,158) |
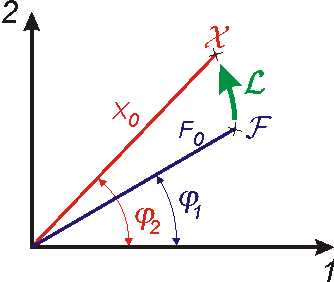 Komplexní čísla
Komplexní čísla
 a
a
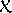 jsou na obr.28 znázorněna v rovině
komplexních čísel. Jejich vzájemný vztah lze vyjádřit tak, že pokládáme komplexní číslo
jsou na obr.28 znázorněna v rovině
komplexních čísel. Jejich vzájemný vztah lze vyjádřit tak, že pokládáme komplexní číslo
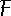 za
za
 násobek komplexního čísla
násobek komplexního čísla
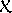 ;
;
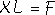 . . |
(4,159) |
Hodnotu komplexního čísla
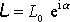 lze získat řešením rovnice
(4,122´)
;
postupem stejným, jakým bylo určeno komplexní číslo
lze získat řešením rovnice
(4,122´)
;
postupem stejným, jakým bylo určeno komplexní číslo
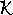 při řešení rovnice
(4,122)
. Dostaneme
tak vyjádření analogické rovnici
(4,150)
:
při řešení rovnice
(4,122)
. Dostaneme
tak vyjádření analogické rovnici
(4,150)
:
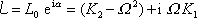 . . |
(4,160) |
Hodnota
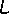 závisí pouze na konstantách
závisí pouze na konstantách
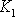 ,
,
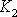 z rovnice
(4,122´)
a na frekvenci
z rovnice
(4,122´)
a na frekvenci
 . Řešením algebraické rovnice
(4,159)
lze pak rychle, ze známé pravé strany
. Řešením algebraické rovnice
(4,159)
lze pak rychle, ze známé pravé strany
 rovnice
(4,122´)
, určit její řešení
rovnice
(4,122´)
, určit její řešení
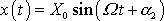 pro různé frekvence
pro různé frekvence
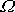 a případně hledat, jak řešení závisí na
konstantách
a případně hledat, jak řešení závisí na
konstantách
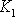 ,
,
 . Někdy též dle rovnice
(4,159)
určujeme neznámé
. Někdy též dle rovnice
(4,159)
určujeme neznámé
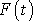 ke známému
ke známému
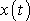 .
.
Pro konkrétní řešení problémů rozepíšeme rovnici (4,159) na rovnici
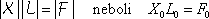 , , |
(4,161) |
která platí mezi absolutními hodnotami komplexních čísel a na rovnici
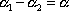 , , |
(4,162) |
která platí mezi argumenty komplexních čísel
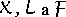 . Rozepíšeme-li totiž rovnici
(4,159)
, dostáváme
. Rozepíšeme-li totiž rovnici
(4,159)
, dostáváme
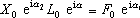 |
a jelikož dle
(4,161)
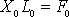 , zřejmě
, zřejmě
 neboli
neboli
 a přechod k rovnici
(4,162)
je již triviální.
a přechod k rovnici
(4,162)
je již triviální.
Hodnotu
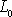 v rovnici
(4,161)
získáme jako absolutní hodnotu
v rovnici
(4,161)
získáme jako absolutní hodnotu
 komplexního čísla
(4,160)
a argument
komplexního čísla
(4,160)
a argument
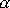 stanovíme z rovnice
stanovíme z rovnice
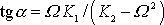 , která vyjadřuje známou skutečnost, že tangens argumentu komplexního čísla je
poměrem jeho imaginární a reálné části.
, která vyjadřuje známou skutečnost, že tangens argumentu komplexního čísla je
poměrem jeho imaginární a reálné části.
V konkrétním případě rovnice
(4,122)
je komplexní číslo
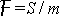 reálné, tedy
reálné, tedy
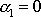 . Komplexní číslo
. Komplexní číslo
 (je-li
(je-li
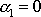 , je dle
(4,162)
, je dle
(4,162)
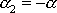 ) a komplexní číslo
) a komplexní číslo
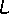 je rovno číslu
je rovno číslu
 zavedenému rovnicí
(4,150)
. Rovnice
(4,159)
dává v tomto konkrétním případě
zavedenému rovnicí
(4,150)
. Rovnice
(4,159)
dává v tomto konkrétním případě
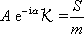 , , |
(4,163) |
což je rovnice shodná s rovnicí
(4,149)
, uvědomíme-li
si, že v rovnici
(4,163)
argument
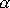 má stejný význam jako argument
má stejný význam jako argument
 v rovnici
(4,149)
. Postup, jak
z rovnice
(4,149)
byly získány rovnice
(4,155)
pro amplitudu ustálených
kmitů a rovnice
(4,156)
pro fázové posunutí vynucující síly a vynuceného kmitu,
ukazuje, jak se získávají z rovnice
(4,159)
rovnice potřebné pro konkrétní
řešení problémů.
v rovnici
(4,149)
. Postup, jak
z rovnice
(4,149)
byly získány rovnice
(4,155)
pro amplitudu ustálených
kmitů a rovnice
(4,156)
pro fázové posunutí vynucující síly a vynuceného kmitu,
ukazuje, jak se získávají z rovnice
(4,159)
rovnice potřebné pro konkrétní
řešení problémů.
Řada fyzikálních problémů vede na řešení rovnice typu
(4,122´)
. Máme-li např. obvod střídavého proudu s odpory, indukčnostmi a
kapacitami, budicí funkcí na pravé straně rovnice
(4,122´)
je střídavé napětí a
na levé straně rovnice místo výchylky x
vystupuje proud protékající obvodem. Hodnoty konstant
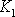 a
a
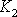 jsou dány způsobem řazení a velikostmi
odporů, indukčností a kapacit. Komplexní číslo
jsou dány způsobem řazení a velikostmi
odporů, indukčností a kapacit. Komplexní číslo
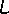 se v tomto případě nahradí obdobně
zavedenou komplexní impedancí obvodu
se v tomto případě nahradí obdobně
zavedenou komplexní impedancí obvodu
 . Podrobněji se lze o řešení sítí střídavého proudu komplexní metodou poučit např. v
. Podrobněji se lze o řešení sítí střídavého proudu komplexní metodou poučit např. v
 . Komplexní čísla k charakteristice systémů podrobené harmonické budící
funkci se užívají též při řešení viskoelastických problémů, kde zavádíme
komplexní elastické moduly, při vyšetřování dielektrických vlastností látek ve
střídavých elektrických polích, pro jejichž charakteristiku zavádíme komplexní
permitivitu a v řadě dalších případů (viz např.
. Komplexní čísla k charakteristice systémů podrobené harmonické budící
funkci se užívají též při řešení viskoelastických problémů, kde zavádíme
komplexní elastické moduly, při vyšetřování dielektrických vlastností látek ve
střídavých elektrických polích, pro jejichž charakteristiku zavádíme komplexní
permitivitu a v řadě dalších případů (viz např.
 , 2. díl).
, 2. díl).
Ve všech uvedených případech mohou vzhledem ke stejnému charakteru rovnic s podrobně vyšetřovaným mechanickým případem nastat rezonanční jevy. Nejznámější jsou rezonanční jevy v elektrických obvodech střídavého proudu, kde při určitém seskupení indukčností a kapacit nastávají při vhodných frekvencích rezonance proudu nebo napětí. Rezonanční jevy se projevují také ve složitějších mechanických systémech, než je ten, který je popsán rovnicí (4,122) . Máme-li nějakou složitější mechanickou konstrukci, např. nějaký dopravní prostředek, může být určitá část této konstrukce vybuzena slabou vnější silou vhodné frekvence k velikým výchylkám. Omezit takové, většinou nežádoucí, rezonance, je úkolem konstruktérů. Při konstrukci dopravních prostředků, na které z vnějšku i od pohybujících se součástí motoru působí budicí síly nejrůznějších frekvencí, bývá takový úkol dosti obtížný.