Budeme vyšetřovat pohyb hmotného bodu vázaného na přímku, na
nějž vedle elastické síly uvažované v rovnici
(2,10)
působí ještě odporující
síla
(4,57)
. Položíme-li do přímky, podél které se může hmotný bod pohybovat,
souřadnicovou osu x
s počátkem v místě, k němuž směřuje elastická síla, bude tato síla
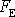 vyjádřena rovnicí
vyjádřena rovnicí
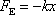 |
(4,68) |
a odporující síla (4,57) rovnicí
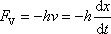 , , |
(4,69) |
kde k a h jsou kladné konstanty,
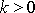 ,
,
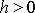 . (V rovnici
(4,69)
jsme konstantu síly
(4,57)
označili h, abychom ji odlišili
od konstanty v rovnici
(4,68)
). Pohybová rovnice hmotného bodu o hmotnosti m,
na nějž působí síly
(4,68)
a
(4,69)
má tvar
. (V rovnici
(4,69)
jsme konstantu síly
(4,57)
označili h, abychom ji odlišili
od konstanty v rovnici
(4,68)
). Pohybová rovnice hmotného bodu o hmotnosti m,
na nějž působí síly
(4,68)
a
(4,69)
má tvar
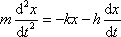 . . |
(4,70) |
Zavedeme-li označení
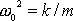 a
a
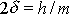 , lze po zřejmé úpravě přepsat rovnici
(4,70)
na tvar
, lze po zřejmé úpravě přepsat rovnici
(4,70)
na tvar
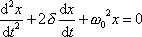 . . |
(4,71) |
Symbol
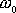 odpovídá (viz rovnici
(2,12)
) frekvenci
harmonického kmitu
(2,14)
, který je řešením rovnice
(2,10)
, tj. rovnice
(4,71)
pro netlumený případ
odpovídá (viz rovnici
(2,12)
) frekvenci
harmonického kmitu
(2,14)
, který je řešením rovnice
(2,10)
, tj. rovnice
(4,71)
pro netlumený případ
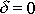 . Frekvenci
. Frekvenci
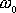 budeme dále nazývat frekvencí netlumeného
harmonického kmitu nebo též vlastní frekvencí harmonického oscilátoru
. V této kapitole budeme pro kruhové
(úhlové) frekvence
budeme dále nazývat frekvencí netlumeného
harmonického kmitu nebo též vlastní frekvencí harmonického oscilátoru
. V této kapitole budeme pro kruhové
(úhlové) frekvence
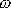 užívat, jak je při výkladu kmitů běžné,
stručného označení frekvence. Při konkrétních výpočtech je si třeba uvědomit,
že takto označená frekvence je
užívat, jak je při výkladu kmitů běžné,
stručného označení frekvence. Při konkrétních výpočtech je si třeba uvědomit,
že takto označená frekvence je
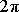 - násobkem lineární frekvence f (viz rov.
(1,28)
).
- násobkem lineární frekvence f (viz rov.
(1,28)
).
Rovnice
(4,71)
je lineární diferenciální rovnice s konstantními
koeficienty druhého řádu. Obecné řešení takové rovnice získáme, najdeme-li dvě
lineárně nezávislé funkce
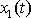 a
a
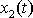 , které řeší tuto rovnici, jak jsme již uvedli při řešení rovnice
(2,10)
. Zopakujeme
tam vysvětlené pojmy. Lineárně nezávislé jsou takové dvě funkce
, které řeší tuto rovnici, jak jsme již uvedli při řešení rovnice
(2,10)
. Zopakujeme
tam vysvětlené pojmy. Lineárně nezávislé jsou takové dvě funkce
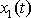 a
a
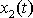 , kde jednu z druhé nelze získat vynásobením stejnou konstantou C
pro celý obor nezávisle proměnné;
, kde jednu z druhé nelze získat vynásobením stejnou konstantou C
pro celý obor nezávisle proměnné;
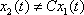 . . |
(4,72) |
Lineární kombinací funkcí
 a
a
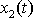 rozumíme výraz
rozumíme výraz
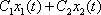 , , |
(4,73) |
kde
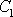 a
a
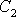 jsou libovolné konstanty. Tvrzení, že
obecným řešením rovnice
(4,71)
je výraz
(4,73)
znamená, že každou funkci
jsou libovolné konstanty. Tvrzení, že
obecným řešením rovnice
(4,71)
je výraz
(4,73)
znamená, že každou funkci
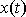 , která je řešením rovnice
(4,71)
, lze zapsat ve tvaru
(4,73)
, tedy
, která je řešením rovnice
(4,71)
, lze zapsat ve tvaru
(4,73)
, tedy
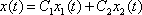 . . |
(4,74) |
Hodnoty konstant
 a
a
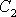 lze určit z počátečních podmínek
pohybu. (Meze platnosti zde uvedených tvrzení a odkazy na literaturu, v níž lze
najít jejich důkazy viz
lze určit z počátečních podmínek
pohybu. (Meze platnosti zde uvedených tvrzení a odkazy na literaturu, v níž lze
najít jejich důkazy viz
 , kap. 17.)
, kap. 17.)
Snadno se lze přesvědčit, že řešením rovnice (4,71) je funkce
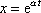 . . |
(4,75) |
Provedeme první a druhou derivaci funkce (4,75)
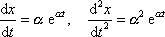 |
a všechny tři poslední výrazy dosadíme do rovnice (4,71) . Dostaneme rovnici
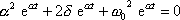 , , |
(4,76) |
kterou lze zřejmě splnit pro všechna t, lze-li splnit algebraickou rovnici
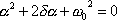 . . |
(4,77) |
Vždy nenulový výraz
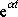 je totiž možno v rovnici
(4,76)
zkrátit.
je totiž možno v rovnici
(4,76)
zkrátit.
Rovnice
(4,77)
se nazývá charakteristická rovnice
k rovnici
(4,71)
. Charakteristická
rovnice
(4,77)
je kvadratickou rovnicí pro dosud neurčenou konstantu
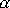 . Jejím řešením získáme dvě hodnoty
. Jejím řešením získáme dvě hodnoty
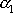 ,
,
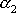 dané rovnicí
dané rovnicí
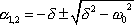 . . |
(4,78) |
Funkce
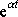 je řešením rovnice
(4,71)
, položíme-li
je řešením rovnice
(4,71)
, položíme-li
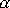 rovné jedné z hodnot daných rovnicí
(4,78)
. S výjimkou případu
rovné jedné z hodnot daných rovnicí
(4,78)
. S výjimkou případu
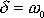 získáme dvě lineárně nezávislé funkce
získáme dvě lineárně nezávislé funkce
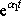 a
a
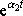 , které řeší rovnici
(4,71)
. Funkce
, které řeší rovnici
(4,71)
. Funkce
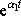 a
a
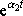 jsou lineárně nezávislé, protože nelze najít
konstantu, kterou by bylo možno vynásobit funkci
jsou lineárně nezávislé, protože nelze najít
konstantu, kterou by bylo možno vynásobit funkci
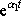 , abychom dostali funkci
, abychom dostali funkci
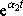 , jsou-li
, jsou-li
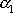 a
a
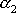 dvě různé konstanty. Pro
dvě různé konstanty. Pro
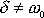 tak dostaneme obecné řešení rovnice
(4,71)
tak dostaneme obecné řešení rovnice
(4,71)
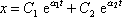 . . |
(4,79) |
Konstanty
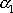 a
a
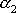 dávají dvě nezávislá řešení charakteristické
rovnice
(4,77)
.
dávají dvě nezávislá řešení charakteristické
rovnice
(4,77)
.
V případě
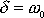 dá právě uvedený postup pouze jednu
funkci
dá právě uvedený postup pouze jednu
funkci
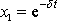 , která řeší rovnici
(4,71)
. Druhou lineárně nezávislou funkcí řešící rovnici
(4,71)
je v případě
, která řeší rovnici
(4,71)
. Druhou lineárně nezávislou funkcí řešící rovnici
(4,71)
je v případě
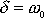 funkce
funkce
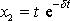 . Dosadíme-li funkci
. Dosadíme-li funkci
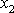 a její první i druhou derivaci do rovnice
(4,71)
, dostaneme
a její první i druhou derivaci do rovnice
(4,71)
, dostaneme
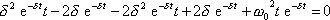 . . |
Když
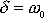 , právě zapsaná rovnice je splněna pro všechna t
a funkce
, právě zapsaná rovnice je splněna pro všechna t
a funkce
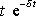 je řešením rovnice
(4,71)
. Obecné řešení
rovnice
(4,71)
v případě, že
je řešením rovnice
(4,71)
. Obecné řešení
rovnice
(4,71)
v případě, že
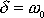 má tedy tvar
má tedy tvar
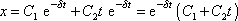 . . |
(4,80) |
Pohyb hmotného bodu vázaného na přímku, na který působí síly
(4,68)
a
(4,69)
, je různý podle poměru velikosti elastické síly
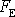 a odporující (tlumící) síly
a odporující (tlumící) síly
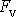 . Rozdělení provádíme dle konstant
. Rozdělení provádíme dle konstant
 a
a
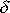 , které velikosti těchto sil vyjadřují v rovnici
(4,71)
.
, které velikosti těchto sil vyjadřují v rovnici
(4,71)
.
Budeme rozlišovat tři případy a
pohyby, které vzniknou, budeme nazývat takto:
a)
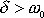 aperiodický,
aperiodický,
b)
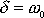 mezní aperiodický,
mezní aperiodický,
c)
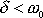 , tlumený harmonický kmit.
, tlumený harmonický kmit.
Jako první vyšetříme podrobněji pohyb označený
v předchozí tabulce a). Jedná se o pohyb, který vznikne ve vyšetřovaném
poli elastické
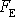 a tlumicí
a tlumicí
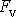 síly v případě, kdy tlumení je velké, a
tedy
síly v případě, kdy tlumení je velké, a
tedy
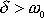 .
.
Je-li
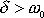 , je výraz pod odmocninou v rovnici
(4,78)
kladný. Odmocninu označíme
, je výraz pod odmocninou v rovnici
(4,78)
kladný. Odmocninu označíme
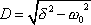 . . |
(4,81) |
Výrazy
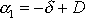 a
a
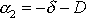 jsou pak reálná čísla a rovnici pohybu
v souřadnicové ose x
, tj. rovnici
(4,79)
, můžeme zapsat
v tvaru
jsou pak reálná čísla a rovnici pohybu
v souřadnicové ose x
, tj. rovnici
(4,79)
, můžeme zapsat
v tvaru
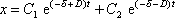 . . |
(4,82) |
Jelikož
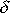 jakožto poměr kladných veličin
jakožto poměr kladných veličin
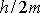 je kladné
je kladné
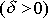 a dle
(4,81)
platí
a dle
(4,81)
platí
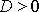 a
a
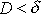 , jsou konstanty
, jsou konstanty
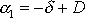 i
i
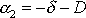 záporné, a tedy výchylka x
v rovnici
(4,82)
konverguje k nule
pro rostoucí hodnoty času t;
záporné, a tedy výchylka x
v rovnici
(4,82)
konverguje k nule
pro rostoucí hodnoty času t;
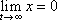 . . |
(4,83) |
Obdobně jako výchylka x i rychlost pohybu
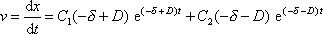 |
(4,84) |
konverguje k nule pro neomezeně rostoucí t;
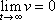 . . |
(4,85) |
Hmotný bod při pohybu popsaném rovnicí (4,82) se nakonec vždy zastaví v počátku soustavy souřadnic, tj. v bodě, ke kterému směřuje elastická síla (4,68) . Nachází-li se hmotný bod v tomto bodě, říkáme, že zaujímá rovnovážnou polohu.
Typickou vlastností aperiodického pohybu je, že průchod
hmotného bodu rovnovážnou polohou nastává pro konečné hodnoty času t
nejvýše jednou. Položíme-li v rovnici
(4,82)
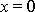 , dostáváme
, dostáváme
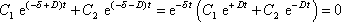 , , |
a protože
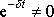 pro konečná t, položíme
pro konečná t, položíme
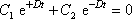 |
a odtud
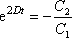 . . |
Poslední rovnice má jedno řešení, je-li
 , a omezíme-li se na případ
, a omezíme-li se na případ
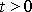 dokonce jen pro
dokonce jen pro
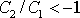 . Pro
. Pro
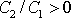 nemá žádné řešení. Je-li jedna
z konstant
nemá žádné řešení. Je-li jedna
z konstant
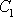 ,
,
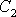 kladná a druhá záporná a jejich absolutní
hodnoty splňují podmínku
kladná a druhá záporná a jejich absolutní
hodnoty splňují podmínku
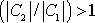 , projde hmotný bod při aperiodickém pohybu jednou rovnovážnou polohou pro
konečné
, projde hmotný bod při aperiodickém pohybu jednou rovnovážnou polohou pro
konečné
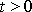 , jinak rovnovážnou polohu zaujme až pro
, jinak rovnovážnou polohu zaujme až pro
 . Neuvažujeme triviální případ
. Neuvažujeme triviální případ
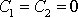 , kdy hmotný bod je po celou dobu v rovnovážné poloze.
, kdy hmotný bod je po celou dobu v rovnovážné poloze.
Ukážeme, jak vypadají řešení (4,82) pro dvě typické volby počátečních podmínek. Nejprve pro počáteční podmínky
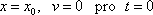 , , |
(4,86) |
které odpovídají případu, kdy hmotný bod vychýlíme z rovnovážné polohy a volně (bez udělení počáteční rychlosti) jej vypustíme. Potom pro počáteční podmínky
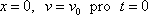 , , |
(4,87) |
které odpovídají případu, kdy hmotný bod uvedeme do pohybu
tím, že mu v rovnovážné poloze udělíme nenulovou rychlost
 .
.
Z rovnic
(4,82)
a
(4,84)
dostáváme pro počáteční
podmínky
(4,86)
soustavu dvou algebraických rovnic (členy
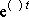 po dosazení
po dosazení
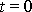 dají jednotku;
dají jednotku;
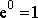 ):
):
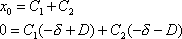 , , |
(4,88) |
jejichž řešením určíme konstanty
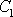 a
a
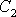 :
:
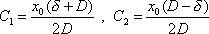 . . |
Dosazením těchto konstant do rovnice (4,82) dostáváme po úpravě rovnici aperiodického pohybu pro počáteční podmínky (4,86)
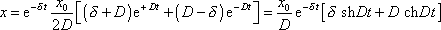 . . |
(4,89) |
V posledním vyjádření funkce
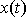 jsme užili funkce hyperbolický sinus (znak
sh) a hyperbolický kosinus (znak ch), které jsou definovány následujícími
vztahy
jsme užili funkce hyperbolický sinus (znak
sh) a hyperbolický kosinus (znak ch), které jsou definovány následujícími
vztahy
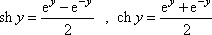 . . |
(4,90) |
Podrobněji o hyperbolických funkcích se lze poučit v
 , kap. 2.
, kap. 2.
Pro počáteční podmínky
(4,87)
dají rovnice
(4,82)
a
(4,84)
pro určení konstant
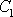 a
a
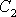 algebraické rovnice
algebraické rovnice
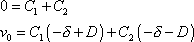 , , |
jejichž řešením dostáváme
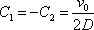 . . |
Tedy pro počáteční podmínky (4,87) aperiodický pohyb je popsán funkcí
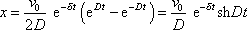 . . |
(4,91) |
Graficky je funkce
(4,89)
pro hodnoty
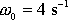 ,
,
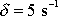 a
a
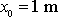 znázorněna jako křivka 1 na obr.23 a funkce
(4,91)
pro hodnoty
znázorněna jako křivka 1 na obr.23 a funkce
(4,91)
pro hodnoty
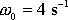 ,
,
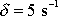 a
a
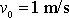 jako křivka 1 na obr.24. Hodnota
jako křivka 1 na obr.24. Hodnota
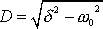 je pro obě funkce stejná a rovna
je pro obě funkce stejná a rovna
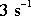 .
.
Případ b) z výše uvedené tabulky, kdy
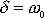 , tj. mezní aperiodický pohyb je popsán rovnicí
, tj. mezní aperiodický pohyb je popsán rovnicí
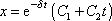 , , |
(4,80) |
jeho rychlost je
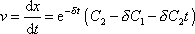 . . |
(4,92) |
 Z těchto rovnic plyne, že vlastnosti
(4,83)
a
(4,85)
jsou splněny i pro mezní aperiodický
pohyb. Anulováním rovnice
(4,80)
zjistíme, že pro konečné hodnoty t
projde hmotný bod rovnovážnou polohou pou-ze
pro
Z těchto rovnic plyne, že vlastnosti
(4,83)
a
(4,85)
jsou splněny i pro mezní aperiodický
pohyb. Anulováním rovnice
(4,80)
zjistíme, že pro konečné hodnoty t
projde hmotný bod rovnovážnou polohou pou-ze
pro
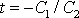 , tedy pro kladná t(
, tedy pro kladná t(
 ) jen
když konstanty
) jen
když konstanty
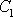 a
a
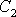 mají opačná znaménka. Průběh pohybu se
podobně jako v předcházejícím pří-padě neopakuje, proto i tento pohyb
nazýváme aperiodickým.
mají opačná znaménka. Průběh pohybu se
podobně jako v předcházejícím pří-padě neopakuje, proto i tento pohyb
nazýváme aperiodickým.
Při počátečních podmín-kách
(4,86)
dostáváme z rovnice
(4,80)
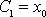 a
a
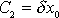 . Po dosazení vypočtených hodnot
. Po dosazení vypočtených hodnot
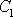 a
a
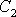 do rovnice
(4,80)
dostáváme
do rovnice
(4,80)
dostáváme
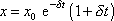 . . |
(4,93) |
Pro počáteční podmínky
(4,87)
z rovnic
(4,80)
a
(4,92)
dostáváme přímo hodnoty
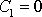 ,
,
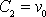 . Pohyb je pak popsán rovnicí
. Pohyb je pak popsán rovnicí
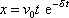 . . |
(4,94) |
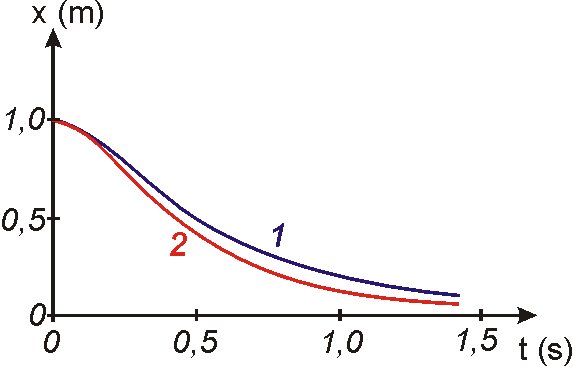
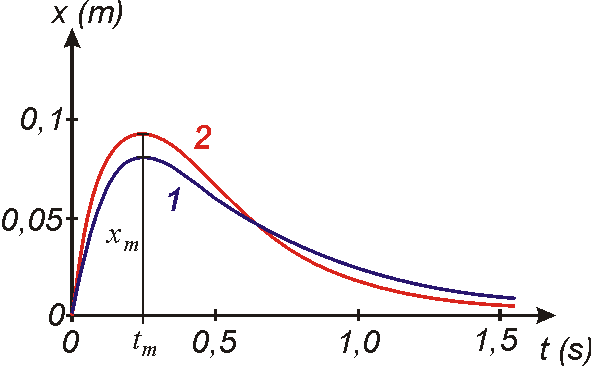 Jako křivka označená číslem 2 je na obr.23 znázorněna funkce
(4,93)
se stejnými hodnotami
Jako křivka označená číslem 2 je na obr.23 znázorněna funkce
(4,93)
se stejnými hodnotami
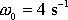 ,
,
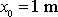 , jako má křivka 1, a s hodnotou tlumení
, jako má křivka 1, a s hodnotou tlumení
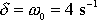 .
.
Podobně křivka 2 na obr.24 od-povídá funkci
(4,94)
se stejnými hodnotami
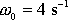 ,
,
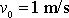 , jako má křivka 1 tohoto obrázku, a s hodnotou tlumení
, jako má křivka 1 tohoto obrázku, a s hodnotou tlumení
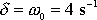 . Rychlejší konvergence křivek 2 k rovnovážné poloze než křivek 1 je obecnou
vlastností mezního aperio-dického pohybu
(4,80)
ve srovnání s pohybem
aperiodickým
(4,82)
. Při porovnání předpokládáme, že frekvence netlumených
harmonických kmitů
. Rychlejší konvergence křivek 2 k rovnovážné poloze než křivek 1 je obecnou
vlastností mezního aperio-dického pohybu
(4,80)
ve srovnání s pohybem
aperiodickým
(4,82)
. Při porovnání předpokládáme, že frekvence netlumených
harmonických kmitů
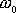 obou pohybů jsou stejné, tedy
předpokládáme-li stejné hmotnosti m
pohybujících se hmotných bodů, musí být stejné i elastické
konstanty k (viz rov.
(4,68)
).
obou pohybů jsou stejné, tedy
předpokládáme-li stejné hmotnosti m
pohybujících se hmotných bodů, musí být stejné i elastické
konstanty k (viz rov.
(4,68)
).
Balistická metoda
Všimneme si nyní vztahu mezi velikostí maximální
výchylky
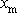 pohybu
(4,94)
vyznačené na obr.24 a
rychlostí
pohybu
(4,94)
vyznačené na obr.24 a
rychlostí
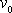 tohoto pohybu v čase
tohoto pohybu v čase
 . Maximální výchylky dosáhne pohyb v čase, kdy derivace
. Maximální výchylky dosáhne pohyb v čase, kdy derivace
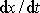 , tj. jeho rychlost
, tj. jeho rychlost
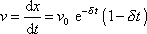 |
(4,95) |
je nulová. Nebudeme-li uvažovat případ
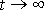 , výraz
(4,95)
bude nulový v čase
, výraz
(4,95)
bude nulový v čase
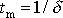 . Dosadíme-li tuto hodnotu za čas t
do rovnice
(4,94)
, dostáváme pro maximální výchylku
. Dosadíme-li tuto hodnotu za čas t
do rovnice
(4,94)
, dostáváme pro maximální výchylku
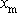 vyjádření
vyjádření
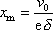 . . |
(4,96) |
Význam rovnice
(4,96)
tkví v tom, že umožňuje určit
rychlost
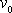 hmotného bodu na začátku pohybu
z hodnoty maximální výchylky
hmotného bodu na začátku pohybu
z hodnoty maximální výchylky
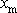 bodu, známe-li tlumící konstantu pohybu
bodu, známe-li tlumící konstantu pohybu
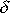 ;
;
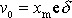 . Experimentálně bývá těžší určit rychlost
. Experimentálně bývá těžší určit rychlost
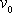 na začátku pohybu než hodnotu maximální
výchylky
na začátku pohybu než hodnotu maximální
výchylky
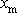 . Tlumící konstantu
. Tlumící konstantu
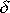 systému lze zpravidla stanovit nezávislým
pokusem, když např. uvedeme systém do pohybu známou rychlostí
systému lze zpravidla stanovit nezávislým
pokusem, když např. uvedeme systém do pohybu známou rychlostí
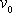 nebo sledujeme jeho pohyb za jiných
počátečních podmínek, než jsou podmínky
(4,87)
.
nebo sledujeme jeho pohyb za jiných
počátečních podmínek, než jsou podmínky
(4,87)
.
Základním příkladem využití rovnice
(4,96)
pro stanovení
rychlosti
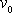 je případ, kdy těleso o hmotnosti m
podrobené silám
(4,68)
a
(4,69)
je vychýleno
z rovnovážné polohy tím, že je zasaženo střelou pohybující se ve směru
osy x
rychlostí
je případ, kdy těleso o hmotnosti m
podrobené silám
(4,68)
a
(4,69)
je vychýleno
z rovnovážné polohy tím, že je zasaženo střelou pohybující se ve směru
osy x
rychlostí
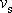 . Ze známého (viz
. Ze známého (viz
 ) zákona zachování hybnosti (viz též čl.
5.4), má-li střela hmotnost
) zákona zachování hybnosti (viz též čl.
5.4), má-li střela hmotnost
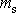 , plyne pro rychlost
, plyne pro rychlost
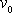 tělesa po zasažení střelou,
tělesa po zasažení střelou,
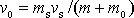 . Změříme-li výchylku
. Změříme-li výchylku
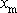 tělesa a známe-li tlumící konstantu
tělesa a známe-li tlumící konstantu
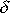 systému a hmotnosti
systému a hmotnosti
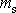 a m, můžeme stanovit jinak obtížně
měřitelnou rychlost střely
a m, můžeme stanovit jinak obtížně
měřitelnou rychlost střely
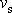 . Z uvedeného příkladu dostala metoda měření rychlostí na základě rovnice
(4,96)
jméno, nazývá se balistická metoda a výchylce
. Z uvedeného příkladu dostala metoda měření rychlostí na základě rovnice
(4,96)
jméno, nazývá se balistická metoda a výchylce
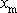 se říká balistická výchylka (
se říká balistická výchylka (
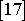 , čl.2.2.1.2).
, čl.2.2.1.2).
Úmyslně jsme zatím při popisu příkladu nezdůraznili pro
použití rovnice
(4,96)
nutný předpoklad, že systém zasažený střelou bude
v mezním aperiodickém stavu. Tento předpoklad není totiž pro použití
balistické metody podstatný. Rovnici analogickou rovnici
(4,96)
lze odvodit i
pro aperiodický pohyb a pro tlumený harmonický kmit. Je-li
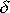 podstatně větší než
podstatně větší než
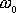 , nejsou podmínky pro balistickou metodu experimentálně vhodné. Užití balistické
metody při tlumených harmonických kmitech je experimentálně vhodné, pouze
rovnice analogická rovnici
(4,96)
je složitější. Nejběžněji se balistická
metoda užívá u slabě tlumených systémů balistických kyvadel,
u kterých tlumení zanedbáváme a velikost
výchylky počítáme z předpokladu, že kinetická energie kyvadla
bezprostředně po zásahu střelou se rovná jeho potenciální energii při maximální
výchylce.
, nejsou podmínky pro balistickou metodu experimentálně vhodné. Užití balistické
metody při tlumených harmonických kmitech je experimentálně vhodné, pouze
rovnice analogická rovnici
(4,96)
je složitější. Nejběžněji se balistická
metoda užívá u slabě tlumených systémů balistických kyvadel,
u kterých tlumení zanedbáváme a velikost
výchylky počítáme z předpokladu, že kinetická energie kyvadla
bezprostředně po zásahu střelou se rovná jeho potenciální energii při maximální
výchylce.
Balistická metoda není ve fyzice omezena na měření rychlostí
střel, ale je široce využita i v jiných oblastech, kde lze převést měření
diferenciální veličiny (původně rychlosti) na integrální veličinu (původně
výchylku). Rovnice analogická rovnici
(4,71)
popisuje pohyb cívky galvanometru.
Pro měření některých elektrických veličin se užívá balistické metody na
speciálně k tomu účelu upraveném balistickém galvanometru. Popis této a
některých dalších balistických metod lze nalézt. v
 v prvním i druhém dílu.
v prvním i druhém dílu.
Tlumeným harmonickým kmitem nazýváme řešení
(4,79)
rovnice
(4,71)
v případě
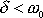 , tedy v případě označeném v tabulce na str.89 jako c). V tomto
případě
, tedy v případě označeném v tabulce na str.89 jako c). V tomto
případě
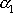 i
i
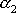 získaná řešením charakteristické rovnice
(4,77)
jsou komplexně sdružená čísla
získaná řešením charakteristické rovnice
(4,77)
jsou komplexně sdružená čísla
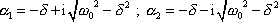 . . |
(4,97) |
Rovnici
(4,79)
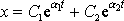 po dosazení konstant
(4,97)
přepíšeme na tvar
po dosazení konstant
(4,97)
přepíšeme na tvar
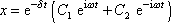 , , |
(4,98) |
kde jsme zavedli označení
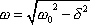 . . |
(4,99) |
Použijeme-li známého (např.
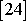 , kap. 1) Moivrova vztahu
, kap. 1) Moivrova vztahu
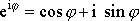 (
(
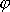 reálné číslo), dostaneme z
(4,98)
reálné číslo), dostaneme z
(4,98)
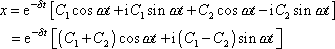 . . |
(4,100) |
Řešení
(4,79)
lze pokládat za řešení rovnice
(4,71)
v komplexním oboru a konstanty
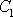 a
a
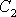 za komplexní čísla. Chceme-li v
(4,100)
získat reálné hodnoty x, je třeba omezit obor volby
komplexních čísel
za komplexní čísla. Chceme-li v
(4,100)
získat reálné hodnoty x, je třeba omezit obor volby
komplexních čísel
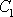 a
a
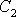 na taková, aby
na taková, aby
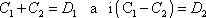 , , |
(4,101) |
kde
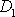 a
a
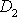 jsou reálná čísla. Podmínky
(4,101)
udávají, že
jsou reálná čísla. Podmínky
(4,101)
udávají, že
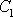 a
a
 musí být komplexně sdružená čísla. Řešení
(4,100)
pro reálná x
lze pak zapsat v tvaru
musí být komplexně sdružená čísla. Řešení
(4,100)
pro reálná x
lze pak zapsat v tvaru
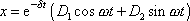 . . |
(4,102) |
Výraz v kulaté závorce je výrazem pro harmonický kmit s frekvencí
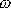 . Lze jej přepsat (viz rovnice
(1,25)
,
(1,29)
a
(1,30)
) na tvar
. Lze jej přepsat (viz rovnice
(1,25)
,
(1,29)
a
(1,30)
) na tvar
 a rovnici pro tlumený harmonický kmit zapsat
v obvyklém tvaru
a rovnici pro tlumený harmonický kmit zapsat
v obvyklém tvaru
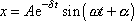 . . |
(4,103) |
Rychlost pohybu (4,103) je
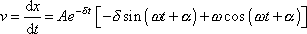 . . |
(4,104) |
V rovnici
(4,103)
A a
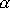 jsou reálné konstanty, jejichž hodnoty lze
určit z počátečních podmínek pohybu. Z tvaru
(4,103)
je zřejmé, proč
právě vyšetřovaný pohyb je nazýván tlumeným harmonickým kmitem, liší se totiž
od harmonického pohybu
(1,25)
pouze tím, že amplituda kmitu není konstantní,
ale je dána výrazem
jsou reálné konstanty, jejichž hodnoty lze
určit z počátečních podmínek pohybu. Z tvaru
(4,103)
je zřejmé, proč
právě vyšetřovaný pohyb je nazýván tlumeným harmonickým kmitem, liší se totiž
od harmonického pohybu
(1,25)
pouze tím, že amplituda kmitu není konstantní,
ale je dána výrazem
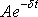 , jehož velikost se s časem zmenšuje. (V rovnici
(4,103)
již
neuvažujeme konstantu
, jehož velikost se s časem zmenšuje. (V rovnici
(4,103)
již
neuvažujeme konstantu
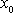 , předpokládáme, že počátek soustavy souřadnic je v rovnovážné poloze.)
Z rovnic
(4,103)
a
(4,104)
plyne, že vlastnosti
(4,83)
a
(4,85)
jsou
splněny i pro tlumený harmonický kmit. Časový průběh pohybu je znázorněn na
obr.25.
, předpokládáme, že počátek soustavy souřadnic je v rovnovážné poloze.)
Z rovnic
(4,103)
a
(4,104)
plyne, že vlastnosti
(4,83)
a
(4,85)
jsou
splněny i pro tlumený harmonický kmit. Časový průběh pohybu je znázorněn na
obr.25.
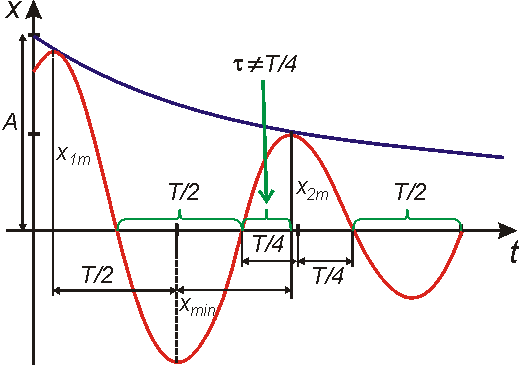 Pohyb
(4,103)
není čistě periodickým pohybem, protože všechny polohy hmotného
bodu nenásledují po sobě v pravidelných časových intervalech, např.
maximální výchylky dosažené při jednom výkyvu hmotného bodu z rovnovážné
polohy hmotný bod již pro žádný následující čas nedosáhne. Řadu vlastností
periodických pohybů však pohyb
(4,103)
zachovává. Průchody hmotného bodu
rovnovážnou polohou nastávají v pravidelných intervalech stejně jako
průchody maximální výchylkou.
Pohyb
(4,103)
není čistě periodickým pohybem, protože všechny polohy hmotného
bodu nenásledují po sobě v pravidelných časových intervalech, např.
maximální výchylky dosažené při jednom výkyvu hmotného bodu z rovnovážné
polohy hmotný bod již pro žádný následující čas nedosáhne. Řadu vlastností
periodických pohybů však pohyb
(4,103)
zachovává. Průchody hmotného bodu
rovnovážnou polohou nastávají v pravidelných intervalech stejně jako
průchody maximální výchylkou.
Tlumený harmonický kmit
(4,103)
na rozdíl od aperiodických
pohybů nabývá hodnoty
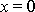 nekonečněkrát, a to vždy, když výraz
nekonečněkrát, a to vždy, když výraz
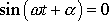 , tedy když
, tedy když
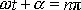 , kde n
je celé číslo. Časový interval
, kde n
je celé číslo. Časový interval
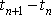 mezi dvěma po sobě následujícími průchody
rovnovážnou polohou zjistíme odečtením rovnic
mezi dvěma po sobě následujícími průchody
rovnovážnou polohou zjistíme odečtením rovnic
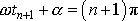 a
a
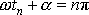 ;
;
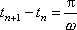 . . |
(4,105) |
Jako dobu kmitu T označíme dvojnásobnou hodnotu intervalu (4,105) , protože teprve při každém druhém průchodu rovnovážnou polohou se hmotný bod pohybuje ve stejném smyslu (viz obr.25), tedy
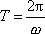 . . |
(4,106) |
Porovnáním s rovnicí
(1,16)
vidíme, že je vhodné
nazvat
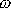 frekvencí, přesněji úhlovou frekvencí tlumeného harmonického kmitu. Z rovnice
(4,99)
,
kterou byla hodnota
frekvencí, přesněji úhlovou frekvencí tlumeného harmonického kmitu. Z rovnice
(4,99)
,
kterou byla hodnota
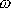 zavedena, plyne, že frekvence
zavedena, plyne, že frekvence
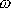 je menší než frekvence
je menší než frekvence
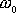 jim odpovídajících netlumených kmitů. Dle
rovnic
(4,105)
a
(1,26)
potom také doba kmitu T
tlumeného harmonického kmitu je delší než doba kmitu
jim odpovídajících netlumených kmitů. Dle
rovnic
(4,105)
a
(1,26)
potom také doba kmitu T
tlumeného harmonického kmitu je delší než doba kmitu
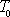 jemu odpovídajícího netlumeného harmonického kmitu,
jemu odpovídajícího netlumeného harmonického kmitu,
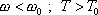 . . |
(4,107) |
Maxima a minima funkce
(4,103)
, tedy krajní výchylky
kmitajícího hmotného bodu, nastávají pro ty časy t, pro které
rychlost v pohybu daná rovnicí
(4,103)
nabývá nulové hodnoty. Pro konečná t rychlost
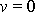 , když
, když
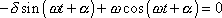 , , |
tedy když
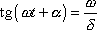 . . |
(4,108) |
Funkce
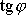 je periodickou funkcí s periodou
je periodickou funkcí s periodou
 , nabývá proto pevně dané hodnoty vždy, když se argument funkce změní o
, nabývá proto pevně dané hodnoty vždy, když se argument funkce změní o
 . Rovnice
(4,108)
bude splněna pro taková t, pro která platí
. Rovnice
(4,108)
bude splněna pro taková t, pro která platí
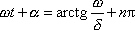 , , |
(4,109) |
kde n
je celé číslo. V rovnici
(4,109)
uvažujeme
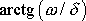 jako hodnotu v intervalu
jako hodnotu v intervalu
 . Zjistíme časový interval mezi dvěma po sobě následujícími časy
. Zjistíme časový interval mezi dvěma po sobě následujícími časy
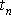 a
a
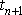 splňujícími rovnici
(4,108)
. Jelikož
splňujícími rovnici
(4,108)
. Jelikož
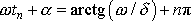 a
a
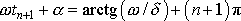 ,
,
získáme odečtením právě napsaných rovnic po elementární úpravě
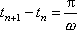 , , |
tedy rovnici shodnou s rovnicí
(4,105)
. Časový interval
mezi dvěma po sobě následujícími extrémy funkce
(4,103)
je stejný jako časový
interval mezi nulovými hodnotami této funkce, a je tedy roven poloviční době
kmitu
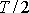 . Jelikož každý druhý extrém funkce je maximum, časový interval mezi maximy je
roven době kmitu T
. Stejný závěr lze vyslovit i pro minima funkce
(4,103)
. Podmínka
pro čas t
, v kterém nastává nulová hodnota funkce
(4,103)
, je
. Jelikož každý druhý extrém funkce je maximum, časový interval mezi maximy je
roven době kmitu T
. Stejný závěr lze vyslovit i pro minima funkce
(4,103)
. Podmínka
pro čas t
, v kterém nastává nulová hodnota funkce
(4,103)
, je
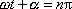 . . |
Porovnáme-li ji s podmínkou
(4,109)
, vidíme, že
vzájemná poloha maxim a nulových hodnot je dána velikostí
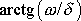 . Porovnáme-li totiž časy
. Porovnáme-li totiž časy
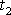 a
a
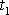 , kdy pro stejná n
jsou splněny podmínky
, kdy pro stejná n
jsou splněny podmínky
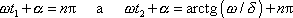 , , |
dostáváme pro časový interval
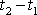 vyjádření
vyjádření
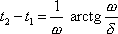 . . |
(4,110) |
Pouze v případě
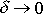 , tj. pro netlumený harmonický kmit, je
, tj. pro netlumený harmonický kmit, je
 a z rovnice
(4,110)
plyne
a z rovnice
(4,110)
plyne
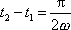 , , |
neboli dle (4,105)
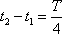 . . |
Pro případ tlumeného harmonického kmitu časový interval mezi
maximem a po něm následující nulovou hodnotou funkce
(4,103)
je různý od
čtvrtiny doby kmitu, jak je zvýrazněno na obr.25. Maxima a minima tlumených
harmonických kmitů neleží v poloviční vzdálenosti mezi nulovými hodnotami
kmitů. Z rovnice
(4,110)
plyne, že maxima a minima jsou posunuta blíže
k časově předcházející nulové hodnotě, protože hodnota
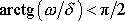 pro nenulové hodnoty d.
pro nenulové hodnoty d.
Konstanty užívané k vystižení míry tlumení
Poměr
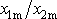 dvou po sobě následujících maxim
dvou po sobě následujících maxim
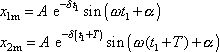 |
funkce (4,103) je roven
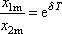 . . |
Zavádíme označení
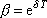 |
(4,111) |
a veličinu
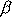 nazýváme útlumem kmitů. Při vyjádření
nazýváme útlumem kmitů. Při vyjádření
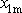 a
a
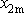 jsme nikde neužili toho, že
jsme nikde neužili toho, že
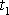 je čas odpovídající maximu funkce
(4,103)
.
Tedy útlum
je čas odpovídající maximu funkce
(4,103)
.
Tedy útlum
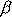 je poměrem libovolných dvou výchylek x,
které zaujme hmotný bod konající tlumený kmit v časovém odstupu rovném
době kmitu T. Přirozený logaritmus
je poměrem libovolných dvou výchylek x,
které zaujme hmotný bod konající tlumený kmit v časovém odstupu rovném
době kmitu T. Přirozený logaritmus
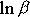 útlumu
útlumu
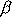 se nazývá logaritmický dekrement útlumu a užijeme pro něj symbol
se nazývá logaritmický dekrement útlumu a užijeme pro něj symbol
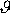 ;
;
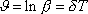 . . |
(4,112) |
Vedle logaritmického dekrementu útlumu
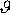 definovaného rovnicí
(4,112)
bývá zaváděn
též dekadický logaritmický dekrement útlumu
definovaného rovnicí
(4,112)
bývá zaváděn
též dekadický logaritmický dekrement útlumu
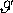 jako dekadický logaritmus
jako dekadický logaritmus
 útlumu
útlumu
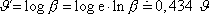 . . |
(4,113) |
Doba
 , za kterou obálka
, za kterou obálka
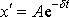 kmitu
(4,103)
čárkovaně vyznačená na obr.25
klesne na hodnotu
kmitu
(4,103)
čárkovaně vyznačená na obr.25
klesne na hodnotu
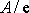 , se nazývá relaxační doba. Z rovnice
, se nazývá relaxační doba. Z rovnice
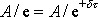 plyne pro relaxační dobu podmínka
plyne pro relaxační dobu podmínka
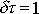 , a odtud
, a odtud
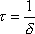 . . |
(4,114) |
Spočítáme, kolik maxim počet označíme n
nastane za čas
 . Časový interval
. Časový interval
 začneme počítat od okamžiku
začneme počítat od okamžiku
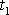 , kdy nastane maximální výchylka
, kdy nastane maximální výchylka
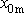 . Toto maximum nebudeme uvažovat do hledaného počtu n. Poslední maximální
výchylka v časovém intervalu bude výchylka
. Toto maximum nebudeme uvažovat do hledaného počtu n. Poslední maximální
výchylka v časovém intervalu bude výchylka
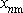 , výchylka
, výchylka
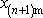 už nastane mimo časový interval
už nastane mimo časový interval
 . Na začátku časového intervalu
. Na začátku časového intervalu
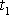 je souřadnice obálky
je souřadnice obálky
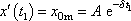 , , |
na konci intervalu
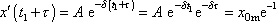 . . |
Pro hodnoty
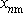 a
a
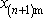 platí nerovnosti
platí nerovnosti
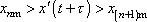 , , |
z kterých plyne
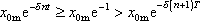 , , |
uvědomíme-li si, že
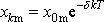 (k je libovolné přirozené číslo) a
(k je libovolné přirozené číslo) a
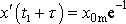 . Porovnáme-li exponenty v poslední nerovnici, dostaneme
. Porovnáme-li exponenty v poslední nerovnici, dostaneme
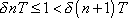 . . |
Odtud pro hledaný počet n
maxim za časový interval
 plyne nerovnost
plyne nerovnost
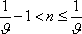 , , |
(4,115) |
kde jsme dle
(4,112)
výraz
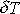 nahradili logaritmickým dekrementem
nahradili logaritmickým dekrementem
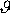 . Nerovnosti
(4,115)
ukazují, jak převrácená hodnota logaritmického dekrementu
udává počet kmitů, po kterých hodnota maximální výchylky klesne na (1/e)-tinu
své původní hodnoty.
. Nerovnosti
(4,115)
ukazují, jak převrácená hodnota logaritmického dekrementu
udává počet kmitů, po kterých hodnota maximální výchylky klesne na (1/e)-tinu
své původní hodnoty.
Tlumené kmity při standardní volbě počátečních podmínek
Tvar rovnice
(4,103)
pro počáteční podmínky
(4,86)
a
(4,87)
dostaneme, dosadíme-li tyto podmínky do rovnic
(4,103)
a
(4,104)
. Pro počáteční
podmínky
(4,86)
tak získáme rovnici kmitu
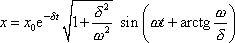 |
(4,116) |
a pro počáteční podmínky (4,87)
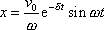 . . |
(4,117) |
Rovnice analogické rovnici tlumených kmitů
Rovnice analogické rovnici
(4,71)
popisují chování řady
důležitých fyzikálních i technických systémů. Např. rovnice pro pohyb
galvanometru (
 , str.214) nebo rovnice popisující pohyb pérových vah mají stejný matematický tvar
, str.214) nebo rovnice popisující pohyb pérových vah mají stejný matematický tvar
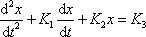 |
(4,118) |
jako rovnice
(4,71)
, pouze na pravé straně rovnic místo nuly
je obecně nenulová konstanta
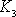 . Konstanty
. Konstanty
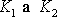 odpovídají konstantám 2d
a
odpovídají konstantám 2d
a
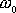 tlumeného kmitu.
tlumeného kmitu.
Má-li lineární diferenciální rovnice s konstantními
koeficienty nenulovou pravou stranu, liší se její obecné řešení od řešení stejné
rovnice bez pravé strany pouze tím, že k obecnému řešení rovnice bez pravé
strany se přičte jedno (tj. řešení bez volitelných konstant) řešení rovnice
s pravou stranou (viz
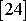 , kap.17). Pro rovnici
(4,118)
je tímto řešením konstantní hodnota
, kap.17). Pro rovnici
(4,118)
je tímto řešením konstantní hodnota
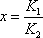 , , |
(4,119) |
jak se lze přesvědčit dosazením hodnoty (4,119) do rovnice (4,118) . Obecné řešení rovnice (4,118) je součet řešení (4,79) rovnice (4,71) a jednoho řešení (4,119) rovnice (4,118) , tedy
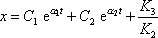 . . |
(4,120) |
V rovnici
(4,120)
jsou
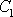 a
a
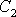 volitelné konstanty a
volitelné konstanty a
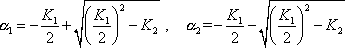 |
kořeny charakteristické rovnice
 . Je to charakteristická rovnice příslušející
rovnici
(4,118)
, neuvažujeme-li u ní pravou stranu.
. Je to charakteristická rovnice příslušející
rovnici
(4,118)
, neuvažujeme-li u ní pravou stranu.
Nenulová hodnota pravé strany rovnice
(4,118)
odpovídá
v rovnici galvanometru momentu síly způsobenému nenulovým proudem
protékajícím cívkou galvanometru, u pérových vah váze váženého předmětu. Tyto
nenulové pravé strany způsobí, že limita řešení
(4,120)
pro
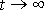 je rovna konstantě
(4,119)
a není nulová
jako limita
(4,83)
řešení
(4,79)
rovnice
(4,71)
. Fyzikálně říkáme, že
rovnovážná poloha systému popsaného rovnicí
(4,118)
je
je rovna konstantě
(4,119)
a není nulová
jako limita
(4,83)
řešení
(4,79)
rovnice
(4,71)
. Fyzikálně říkáme, že
rovnovážná poloha systému popsaného rovnicí
(4,118)
je
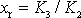 na rozdíl od nulové rovnovážné polohy
na rozdíl od nulové rovnovážné polohy
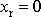 systému popsaného rovnicí
(4,71)
.
systému popsaného rovnicí
(4,71)
.
V uvažovaných systémech se zpravidla určuje
hodnota
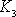 (velikost proudu, váha předmětu) ze změřené
hodnoty
(velikost proudu, váha předmětu) ze změřené
hodnoty
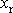 (výchylka galvanometru nebo vah). Způsob,
jakým systém zaujímá rovnovážnou hodnotu, je popsán částí
(výchylka galvanometru nebo vah). Způsob,
jakým systém zaujímá rovnovážnou hodnotu, je popsán částí
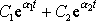 řešení
(4,120)
, tedy funkcí, jejíž analýzu
jsme v tomto článku podrobně provedli. Na velikosti tlumení systému
(galvanometru, vah apod.) záleží, zda rovnovážná poloha bude zaujímána pomalu
(aperiodický stav), rychle (mezní aperiodický stav) nebo zda bude systém kolem
rovnovážné polohy kmitat (tlumený harmonický kmit). U komerčně dodávaných
běžných přístrojů, např. u různých ručkových ampérmetrů, voltmetrů, krámských
vah, bývá systém tlumen tak, aby v provozních podmínkách byl blízko
mezního aperiodického stavu, tj. aby rychle ukázal hodnotu měřené veličiny a
nekmital kolem ní. U laboratorně užívaných systémů, např. u zrcátkových
galvanometrů, je pro každý pokus nutno vhodné tlumení nastavit (viz
řešení
(4,120)
, tedy funkcí, jejíž analýzu
jsme v tomto článku podrobně provedli. Na velikosti tlumení systému
(galvanometru, vah apod.) záleží, zda rovnovážná poloha bude zaujímána pomalu
(aperiodický stav), rychle (mezní aperiodický stav) nebo zda bude systém kolem
rovnovážné polohy kmitat (tlumený harmonický kmit). U komerčně dodávaných
běžných přístrojů, např. u různých ručkových ampérmetrů, voltmetrů, krámských
vah, bývá systém tlumen tak, aby v provozních podmínkách byl blízko
mezního aperiodického stavu, tj. aby rychle ukázal hodnotu měřené veličiny a
nekmital kolem ní. U laboratorně užívaných systémů, např. u zrcátkových
galvanometrů, je pro každý pokus nutno vhodné tlumení nastavit (viz
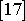 , str. 238). Rozbor řešení
(4,79)
rovnice
(4,71)
provedený v tomto článku je
teoretickým základem pro to, abychom takové vhodné nastavení systému mohli
provést.
, str. 238). Rozbor řešení
(4,79)
rovnice
(4,71)
provedený v tomto článku je
teoretickým základem pro to, abychom takové vhodné nastavení systému mohli
provést.
Nastavení podmínek mezního aperiodického stavu, jako podmínek pro nejrychlejší přechod systému z jedné rovnovážné polohy do druhé, je základní úlohou teorie regulace. Automatická regulace výrobních procesů řízená počítači je stále více využívána. Při ní je však nezbytné, aby impuls měnící průběh regulovaného děje měl správnou velikost a nejrychleji vedl k požadované změně režimu. Proto jsou úvahy podobné těm, které činíme při nastavování mezního aperiodického stavu, pro teorii řízení tak podstatné.