 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
Pozorujeme-li pohyb reálných hmotných objektů, zjišťujeme, že jejich vzájemné působení zabraňuje
vzájemnému pohybu objektů při malých vnějších silách a zpomaluje tento pohyb,
působí-li větší síly. Vzájemné působení reálných hmotných objektů je značně
různorodé a často má složitý charakter, který je třeba pro každý konkrétní
případ podrobně zkoumat. Nejběžnější druhy působení se přibližně vyjadřují
jednoduchými vzorci.
Smýkají-li se dvě tělesa po sobě (viz obr.21), vystihujeme
jejich vzájemné působení silou smykového (vlečného) tření
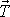, kterou zavádíme jako sílu působící proti pohybu, jejíž velikost je dána výrazem
 . |
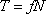(4,55) |
Ve shodě s obr.21 budeme pokládat těleso A za
pohybující se těleso a těleso B za těleso, které je v klidu. Síla
je opačně orientovaná než rychlost
tělesa A. Síla
, která bývá nazývána kolmým tlakem,
je složka do směru kolmého k rovině styčné plochy síly, kterou působí
těleso A na těleso B, a f je součinitel (koeficient)
smykového tření. V přibližném vyjádření
(4,55)
je součinitel
f pokládán za konstantu závislou pouze na druhu vzájemně se smýkajících ploch.
Experimentálně lze zjistit, že k uvedení tělesa A do
pohybu je zapotřebí větší vnější síly než k jeho udržení
v rovnoměrném pohybu. Proto v přibližném vyjádření
(4,55)
se zavádí
pro případ, kdy se těleso uvádí do pohybu z klidu,
statický součinitel smykového tření
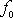, který pro danou dvojici smýkajících se ploch je vždy větší než součinitel f;
. Hodnoty součinitelů f a
lze nalézt v tabulkách fyzikálních konstant (např.
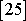), způsob jejich měření je popsán mimo jiné v
.
Odpor, který působí proti valivému pohybu
kola nebo jiného rotačně symetrického tělesa, se přibližně vyjadřuje zavedením
pojmu valivé tření. Valivým třením rozumíme sílu
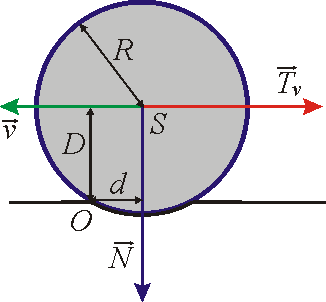
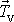, která působí v ose válce proti jeho pohybu (obr.22). Při pohybu válce
(směr pohybu je na obr.22 naznačen vektorem rychlosti
) dochází k deformaci podložky i válce samotného, a proto síla
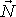, kterou válec tlačí na podložku, vytváří moment síly vůči okamžité ose O otáčení
válce o velikosti
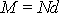. Působiště síly
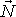klademe do hmotného středu S válce, který
pro předpokládaný homogenní válec leží na rotační ose symetrie válce (viz
čl.5.1). Symbolem d
je na obr.22 označena
vzdálenost od osy otáčení O přímky vedené hmotným středem S válce ve směru
síly
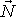. Moment síly o velikosti
působící proti pohybu válce můžeme nahradit
stejně velkým momentem
, když zanedbáme malý rozdíl mezi poloměrem válce R
a vzdáleností D
rotační osy válce od nedeformované podložky.
Pro velikost
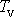síly
, která působí v ose válce proti jeho pohybu, dostáváme pak
z rovnice
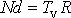vyjádření
. Nahradíme ještě symbol d
obvykle užívaným označením
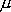pro součinitel valivého tření a dostáváme pro velikost
síly valivého tření vyjádření
 . |
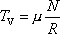(4,56) |
Součinitel valivého tření, který
má rozměr délky, se podobně jako součinitel smykového tření uvádí pro různé
dvojice látek podložky a válce. Jeho hodnoty lze najít v tabulkách (např.
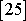). Z rovnice
(4,56)
plyne, že při jinak
stejných podmínkách je valivé tření menší pro válce (kola) s větším
poloměrem R
. V elementárním výkladu nebývá zvykem rozlišovat mezi
statickým a kinetickým valivým třením.
Pro porovnání velikosti smykového
a valivého tření uvedeme příklad. Pro dvojici dřevo dřevo bývá udávána
hodnota součinitele smykového tření f
v okolí hodnoty
a součinitel valivého tření
. Při stejně velkých silách N
vychází v tomto případě pro sílu smykového tření
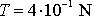a pro sílu valivého tření, má-li válec
poloměr
,
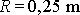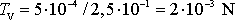. Při valení je v tomto případě síla tření dvěstěkrát menší. Příklad ukazuje
na technickou důležitost převádění smykového pohybu na pohyb valivý (kola,
kuličková ložiska apod.).
Dalším často užívaným typem síly
odporující pohybu je síla
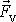úměrná rychlosti
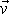pohybujícího se tělesa a mířící proti
pohybu, pro kterou se užívá označení vazká nebo viskózní síla;
 . |
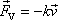(4,57) |
V rovnici
(4,57)
veličina k
je konstantní a kladná
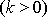. Silou
(4,57)
je např. přibližně vystiženo působení tekutého, tj. kapalného nebo
plynného, prostředí na tuhé těleso při vzájemném pohybu tělesa a prostředí.
Podrobněji tuto otázku rozebereme v druhém svazku knihy (II) při
vyšetřování pohybu těles ve vazkém prostředí. Tam ukážeme, kdy lze odpor
prostředí vystihnout rovnicí typu
(4,57)
, tj. kdy platí Stokesův zákon, a
uvedeme, jak se v něm stanoví velikost konstanty k
ze známých rozměrů tělesa a viskozity
prostředí. V článcích 4.5 a 4.6 budeme při vyšetřování tlumeného a
vynuceného harmonického kmitu užívat pro vystižení odporu prostředí sílu typu
(4,57)
bez bližší specifikace konstanty k
. Aplikovatelnost výsledků bude samozřejmě záviset na tom, do jaké míry v daném případě předpoklad,
že odporující (tlumicí) síla má tvar
(4,57)
, je splněn.
Vyšetříme nyní pohyb tělesa, na které v čase
, kdy těleso mělo nenulovou rychlost, začala působit odporující síla typu
(4,55)
nebo
(4,57)
. Pro výpočet budeme pokládat těleso za hmotný bod o hmotnosti
m a budeme předpokládat, že tento hmotný bod měl v čase
rychlost
. Dále budeme předpokládat, že kromě odporující síly
(4,55)
nebo
(4,57)
žádná
jiná síla na hmotný bod nepůsobí. Uvažované odporující síly mají nulovou složku
ve směru kolmém k rychlosti hmotného bodu
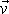, normálová složka zrychlení hmotného bodu je tedy nulová. Z toho plyne, že
vyšetřované pohyby budou přímočaré a budou se konat v přímce, jejíž směr
je dán vektorem
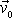. Do tohoto směru položíme souřadnicovou osu x
tak, že její kladný smysl je shodný s kladným smyslem
vektoru
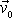a počátek leží v místě, v kterém se hmotný bod nachází v čase
.
Pro pohyb hmotného bodu o hmotnosti m , na nějž působí síla (4,55) , dostáváme pohybovou rovnici
 , |
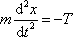(4,58) |
kde síla T
je kladná veličina stálé velikosti. Řešením
rovnice
(4,58)
při výše udaných počátečních podmínkách (
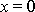a
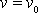v čase
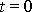) je
 |
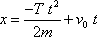(4,59) |
pro časový interval
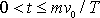. Čas
je čas, pro který rychlost pohybu
(4,59)
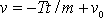nabude nulové hodnoty. V tomto okamžiku pohyb ustává, jelikož zaniká síla T
úměrná rychlosti pohybu. (K vzniku dalšího pohybu by bylo nutno na
těleso zapůsobit vnější silou o velikosti
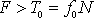, tj. silou větší, než je síla statického tření.) Za dobu
 |
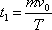(4,60) |
urazí hmotný bod dráhu
 |
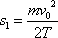(4,61) |
a po proběhnutí této dráhy se zastaví. Právě popsaný pohyb se někdy nazývá pohybem rovnoměrně zpožděným
, neboť v uvažovaném časovém intervalu má jeho zrychlení konstantní zápornou hodnotu
.
K výsledku
(4,61)
lze dojít
též rychleji, užijeme-li větu
(3,11)
o přírůstku kinetické energie soustavy.
Kinetická energie hmotného bodu v čase
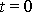je
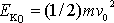, kinetická energie po zastavení hmotného bodu
. Práce vykonaná na hmotný bod po dráze
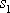silou tření
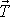, jejíž velikost je dána rovnicí
(4,55)
, je
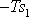. Aplikací rovnice
(3,11)
dostaneme
 , |
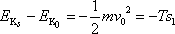odkud po snadné úpravě plyne
rovnice
(4,61)
. Zákon zachování energie
(3,36)
na uvedený příklad užít nelze,
protože síla tření
je nekonzervativní a tudíž neexistuje jí odpovídající potenciální energie.
Pohyb za působení odporující síly
(4,56)
je valivým pohybem tělesa, který bude popsán v čl.7.3. Pro tento
pohyb nemůžeme nahradit těleso hmotným bodem. Pohyb nezáleží pouze na hmotnosti
tělesa m, ale i na jeho momentu setrvačnosti J
(viz kap. 6) a poloměru R.
Bez důkazu uvedeme, že za počátečních podmínek užívaných v tomto článku
pohyb hmotného středu S tělesa je popsán rovnicí tvaru
(4,59)
,
v které hmotnost valícího se tělesa nahradíme výrazem
.
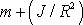Pohybovou rovnici pro pohyb hmotného bodu, na nějž působí síla (4,57) , můžeme zapsat v tvaru
 . |
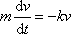(4,62) |
Je to lineární diferenciální
rovnice prvého řádu s konstantními koeficienty. Její obecné řešení (viz
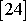, kap. 17) pro hledanou závislost rychlosti v
na čase má tvar
 . |
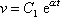(4,63) |
Dosadíme-li funkci (4,63) a její derivaci
 |
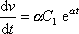do rovnice (4,62) ,
 , |
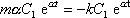zjistíme, že funkcí tvaru
(4,63)
lze splnit rovnici
(4,62)
pro všechna t
při libovolné volbě konstanty
, položíme-li
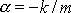. Funkce
 |
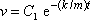(4,64) |
je tedy obecným řešením rovnice (4,62) . Integrací rovnice (4,64) dostaneme pro hledanou závislost souřadnice x hmotného bodu na čase
 . |
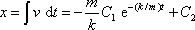(4,65) |
Dosazením počátečních podmínek
,
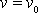pro
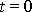do rovnic
(4,64)
a
(4,65)
určíme hodnoty konstant
a
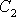. Dostáváme
 . |
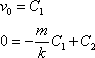První rovnice dává přímo hodnotu konstanty
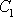a z druhé plyne
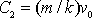. S těmito hodnotami
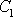a
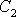dává rovnice
(4,65)
hledanou trajektorii hmotného bodu
 . |
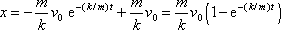(4,66) |
Za působení odporující síly
(4,57)
koná hmotný bod pohyb, při němž jeho rychlost
(4,64)
exponenciálně
klesá, tedy nulové rychlosti nabude až pro
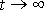. Začne-li uvažovaná odporující síla působit na hmotný bod, který má rychlost
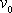, urazí bod v poli této síly dráhu
 , |
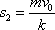(4,67) |
jak plyne z rovnice
(4,66)
,
uvážíme-li její limitní hodnotu pro
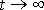. Hmotný bod v poli uvažované odporující síly urazí konečnou vzdálenost
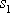za nekonečný časový interval. Hodnota
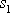je limitní vzdálenost, ke které se hmotný
bod asymptoticky blíží.
Síly
(4,55)
a
(4,57)
působí vždy
v opačném smyslu, než je smysl rychlosti
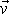hmotného bodu. Uvážíme-li vyjádření práce
dle rovnice
(3,6)
, výkon
 |
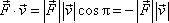je stále záporný. Urazí-li hmotný bod za působení uvažovaných sil nenulový úsek dráhy, práce A vykonaná na něj vnějšími silami je záporná. Síla působící proti pohybu je stálé velikosti, a tedy velikost vykonané práce (viz (3,4) ) je úměrná délce vykonané dráhy. Spojíme-li dvě místa různě dlouhými drahami, práce vykonané uvažovanými silami budou různé. Urazí-li hmotný bod uzavřenou, např. kruhovou dráhu, bude výsledná práce záporná, a tedy nenulová. Obě tyto skutečnosti ukazují, že síly (4,55) a (4,57) jsou nekonzervativní a nelze tedy zavést potenciální energii těchto sil. (Jelikož pohyb za působení síly (4,56) nelze popsat jako pohyb hmotného bodu, je těžší ukázat, ale platí, že i tato síla je nekonzervativní.)
Všimneme-li si pohybů vyšetřovaných v tomto článku, vidíme, že na začátku pohybu měly hmotné
body kinetickou energii
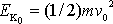a po uražení drah
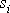daných rovnicemi
(4,61)
a
(4,67)
měly rychlost,
a tedy i kinetickou energii nulovou. Kinetická energie se za působení sil
(4,55)
a
(4,57)
ztratila, rozptýlila, aniž tuto ztrátu můžeme vysvětlit
přírůstkem potenciální energie, kterou pro uvažované síly nelze definovat.
Protože mechanická energie se za působení sil
(4,55)
,
(4,56)
a
(4,57)
ztrácí,
rozptyluje neboli disipuje, nazývají se tyto síly silami disipativními
. Název disipativní síly jsme užili již
v čl.3.4 a tam jsme též uvedli, že za působení disipativních sil neplatí
zákon zachování mechanické energie
(3,16)
a je jej nutno nahradit obecnějším
zákonem
(3,17)
.
|
|
|
|
|
|
|
|
|