Vyšetříme nyní pohyb volného hmotného bodu o hmotnosti m v gravitačním silovém poli, tj. v silovém poli daném rovnicí (4,3)
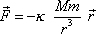 . . |
(4,3) |
Představíme-li si pod bodem o hmotnosti M Slunce a pod bodem o hmotnosti m některou z planet, dostaneme vyřešením zadané úlohy tři Keplerovy zákony o pohybu planet.
Pole popsané rovnicí
(4,3)
je centrální silové pole
. Centrálním silovým polem nazýváme takové
pole, pro které sílu
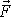 lze psát ve tvaru
lze psát ve tvaru
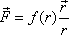 , , |
(4,24) |
kde
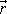 je polohový vektor místa, v němž sílu
uvažujeme. Střed centrální síly je v počátku soustavy souřadnic.
Velikost r vektoru
je polohový vektor místa, v němž sílu
uvažujeme. Střed centrální síly je v počátku soustavy souřadnic.
Velikost r vektoru
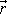 má význam vzdálenosti od středu centrální
síly a
má význam vzdálenosti od středu centrální
síly a
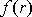 je libovolná funkce vzdálenosti r .
V případě centrální síly
(4,3)
je
je libovolná funkce vzdálenosti r .
V případě centrální síly
(4,3)
je
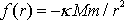 .
.
Pro pohyb hmotného bodu v poli centrálních sil platí,
že moment hybnosti hmotného bodu
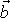 vzhledem ke středu centrální síly je
konstantní. Tedy
vzhledem ke středu centrální síly je
konstantní. Tedy
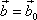 , , |
(4,25) |
kde
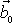 je konstantní vektor. Tvrzení
(4,25)
plyne
bezprostředně z rovnice
(3,36)
, uvědomíme-li si, že v případě pohybu
v poli centrálních sil moment síly vůči středu centrální síly
je konstantní vektor. Tvrzení
(4,25)
plyne
bezprostředně z rovnice
(3,36)
, uvědomíme-li si, že v případě pohybu
v poli centrálních sil moment síly vůči středu centrální síly
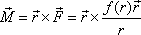 |
je vektorovým součinem dvou rovnoběžných vektorů, a tedy
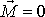 . Dosazením podmínky
. Dosazením podmínky
 do rovnice
(3,36)
, dostáváme rovnici
do rovnice
(3,36)
, dostáváme rovnici
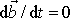 . Výraz, jehož derivace dle času je nulová, je s časem konstantní, tedy
moment hybnosti
. Výraz, jehož derivace dle času je nulová, je s časem konstantní, tedy
moment hybnosti
 v centrálním silovém poli je roven
konstantnímu vektoru, který značíme
v centrálním silovém poli je roven
konstantnímu vektoru, který značíme
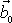 .
.
Je-li moment hybnosti
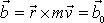 , musí vektory
, musí vektory
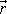 a
a
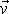 ležet stále v rovině kolmé ke směru
konstantního vektoru
ležet stále v rovině kolmé ke směru
konstantního vektoru
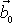 . Pohyb hmotného bodu v centrálním silovém poli je rovinný.
. Pohyb hmotného bodu v centrálním silovém poli je rovinný.
Vektor
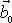 je konstantní, tedy i jeho velikost
je konstantní, tedy i jeho velikost
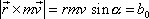 |
(4,26) |
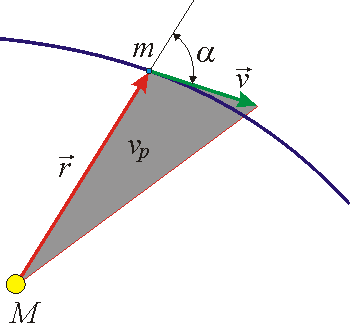 je konstantní. Úhel
je konstantní. Úhel
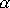 v rovnici
(4,26)
značí úhel mezi
vektory
v rovnici
(4,26)
značí úhel mezi
vektory
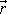 a
a
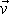 . Výraz
. Výraz
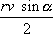 |
bývá nazýván plošnou rychlostí
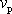 pohybují-cího se hmotného bodu, neboť udává
velikost plochy vyšrafované na obr.19, která v diferen-ciálním přiblížení
je rovna velikosti plochy opsané průvodičem pohybujícího se bodu za jednotku
času. Z rovnice
(4,26)
plyne, že plošná rychlost
pohybují-cího se hmotného bodu, neboť udává
velikost plochy vyšrafované na obr.19, která v diferen-ciálním přiblížení
je rovna velikosti plochy opsané průvodičem pohybujícího se bodu za jednotku
času. Z rovnice
(4,26)
plyne, že plošná rychlost
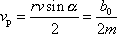 |
je konstantní.
Pohyb hmotného bodu v centrálním silovém poli je rovinný a jeho plošná rychlost je konstantní.
Vrátíme-li se ke gravitačnímu silovému poli
(4,3)
, je
tvrzení o konstantní plošné rychlosti
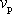 obsahem druhého Keplerova zákona, jehož
obvyklá formulace zní:
obsahem druhého Keplerova zákona, jehož
obvyklá formulace zní:
Plochy opsané průvodičem planety za jednotku času jsou konstantní.
Dle čl.2.3 bychom při hledání pohybu hmotného bodu o hmotnosti m v silovém poli (4,3) měli řešit pohybovou rovnici
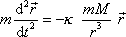 . . |
(4,27) |
Místo tohoto přímého postupu zvolíme jiný, který vede
rychleji k cíli. Využijeme rovnice
(4,25)
a toho, že v gravitačním
poli, které je konzervativní, celková mechanická energie
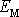 pohybujícího se hmotného bodu je konstantní.
Konstantní hodnotu mechanické energie označíme
pohybujícího se hmotného bodu je konstantní.
Konstantní hodnotu mechanické energie označíme
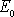 a vyslovené tvrzení můžeme zapsat v tvaru
a vyslovené tvrzení můžeme zapsat v tvaru
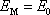 . . |
(4,28) |
Jelikož pohyb je rovinný, jak plyne z rovnice (4,25) , stačí k jeho určení dvě časově proměnné souřadnice, které určíme řešením rovnic (4,26) a (4,28) . Rovnice (4,28) a (4,26) udávají, že při pohybu zůstává zachována celková mechanická energie a velikost momentu hybnosti hmotného bodu.
Pro popis pohybu hmotného bodu v rovině, v které
probíhá, užijeme místo kartézských souřadnic nbsp;
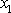 ,
,
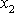 souřadnice polární r,
souřadnice polární r,
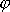 . Vzájemný vztah souřadnic je dán rovnicemi
. Vzájemný vztah souřadnic je dán rovnicemi
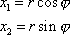 , , |
(4,29) |
 kde r je vzdálenost bodu od společného počátku obou soustav souřadnic a
kde r je vzdálenost bodu od společného počátku obou soustav souřadnic a
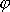 úhel, který průvodič bodu svírá s první
osou kartézské soustavy souřadnic (obr.20). Pracujeme-li s polárními
souřadnicemi, aniž je vztahujeme k nějaké kartézské soustavě souřadnic, je
úhel
úhel, který průvodič bodu svírá s první
osou kartézské soustavy souřadnic (obr.20). Pracujeme-li s polárními
souřadnicemi, aniž je vztahujeme k nějaké kartézské soustavě souřadnic, je
úhel
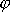 úhlem mezi průvodičem bodu (úsečkou
spojující počátek soustavy s bodem) a nějakou pevně zvolenou přímkou v
rovině. Derivováním rovnic
(4,29)
dle času t dostáváme
úhlem mezi průvodičem bodu (úsečkou
spojující počátek soustavy s bodem) a nějakou pevně zvolenou přímkou v
rovině. Derivováním rovnic
(4,29)
dle času t dostáváme
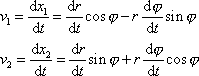 . . |
(4,30) |
Rovnice
(4,26)
a
(4,28)
musíme přepsat tak, aby v nich
vystupovaly dosud neznámé parametrické rovnice
 a
a
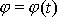 pohybu hmotného bodu. Vektor
pohybu hmotného bodu. Vektor
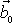 je kolmý k rovině pohybu, proto jediná
jeho nenulová složka v kartézské soustavě souřadnic užité v rovnicích
(4,29)
je třetí složka. Tato složka je rovna velikosti
je kolmý k rovině pohybu, proto jediná
jeho nenulová složka v kartézské soustavě souřadnic užité v rovnicích
(4,29)
je třetí složka. Tato složka je rovna velikosti
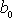 vektoru
vektoru
 . V kartézských souřadnicích třetí složka vektorové rovnice
. V kartézských souřadnicích třetí složka vektorové rovnice
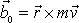 má tedy tvar
má tedy tvar
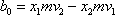 . . |
(4,31) |
Dosadíme-li za
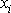 z
(4,29)
a za
z
(4,29)
a za
 z
(4,30)
, dostáváme
z
(4,30)
, dostáváme
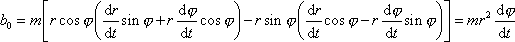 . . |
Výsledek
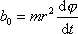 |
(4,32) |
lze též odvodit přímo z rovnice
(4,26)
, když si dle
obr.19 uvědomíme, že výraz
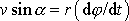 . Rovnici
(4,28)
rozepíšeme,
. Rovnici
(4,28)
rozepíšeme,
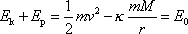 . . |
(4,33) |
V rovnici
(4,33)
jsme použili vyjádření
(4,6)
pro
potenciální energii gravitačního pole. Pro čtverec velikosti rychlosti
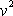 plyne z
(4,30)
plyne z
(4,30)
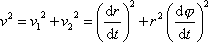 . . |
(4,34) |
Dosazením (4,34) do (4,33) dostáváme
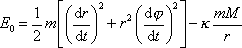 . . |
(4,35) |
Rovnice
(4,32)
a
(4,35)
jsou již hledanou soustavou dvou
diferenciálních rovnic pro určení dvou neznámých funkcí
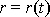 a
a
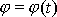 .
Rovnici
(4,35)
upravíme, když vyjádříme
.
Rovnici
(4,35)
upravíme, když vyjádříme
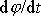 dle rovnice
(4,32)
a zavedeme označení
dle rovnice
(4,32)
a zavedeme označení
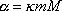 , , |
(4,36) |
na tvar
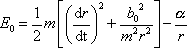 . . |
(4,37) |
Z poslední rovnice lze vypočítat
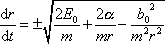 , , |
(4,38) |
a tedy
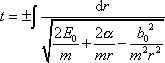 . . |
(4,39) |
Rovnicí
(4,39)
je vyjádřena závislost t na r
, a tím v neexplicitní formě i závislost r na t.
Po vyjádření této závislosti by bylo možné dosazením
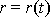 do
(4,32)
vypočítat i
do
(4,32)
vypočítat i
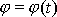 . Při řešení Keplerovy úlohy nás však bude zajímat pouze dráha hmotného bodu,
k jejímuž určení stačí nalézt závislost r na
. Při řešení Keplerovy úlohy nás však bude zajímat pouze dráha hmotného bodu,
k jejímuž určení stačí nalézt závislost r na
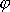 , a není třeba určit časovou závislost obou jeho polárních souřadnic r a
, a není třeba určit časovou závislost obou jeho polárních souřadnic r a
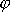 .
.
Derivaci
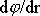 lze podle pravidla o derivování složených funkcí - předpokládáme
lze podle pravidla o derivování složených funkcí - předpokládáme
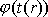 - rozepsat
- rozepsat
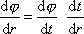 . . |
Hodnotu
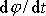 lze určit z rovnice
(4,32)
a hodnotu
lze určit z rovnice
(4,32)
a hodnotu
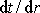 z rovnice
(4,38)
; dostáváme
z rovnice
(4,38)
; dostáváme
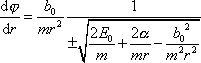 . . |
Pravá strana závisí pouze na r
, a proto lze
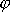 vyjádřit jako neurčitý integrál
vyjádřit jako neurčitý integrál
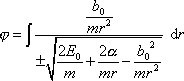 . . |
Primitivní funkce k výrazu pod integrálem jsou
SETEQS2('knihI41do_soubory/eq0044M.gif','knihI41do_soubory/eq0045M.gif','',',',',','5.86','1.76');
o čemž se lze přesvědčit jejich derivováním
dle r
. Výraz s arcuscosinem použijeme pro stanovení závislosti
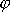 na r , tedy
na r , tedy
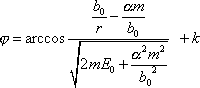 . . |
(4,40) |
Rovnici (4,40) lze přepsat na tvar
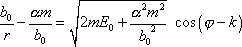 , , |
který po vynásobení konstantou
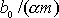 dále upravíme a dostaneme
dále upravíme a dostaneme
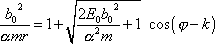 . . |
Poslední rovnice má již tvar polární rovnice kuželosečky (viz dodatek D.3). Zavedeme-li stručné označení konstant, které se v ní vyskytují,
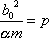 |
(4,41) |
a
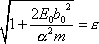 , , |
(4,42) |
dostaneme rovnici
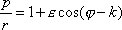 , , |
kterou lze již snadno přepsat na obvykle uváděný tvar polární rovnice kuželoseček
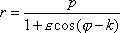 . . |
(4,43) |
Jak vyplývá z odvození v dodatku D.3, rovnice
(4,43)
popisuje vztah mezi
vzdáleností r bodu na kuželosečce od
jednoho jejího ohniska a úhlem
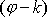 , který průvodič bodu svírá s osou kuželosečky procházející tímto ohniskem.
Konstanta k udává úhel mezi původně
libovolně zvoleným směrem v rovině dráhy a směrem výše uvažované osy
kuželosečky. Konstanta k
je libovolná a odpovídá natočení kuželosečky ve vyšetřované rovině, je
ji možno určit z počátečních podmínek pohybu. V dodatku D.3 je
odvozeno, že pro elipsu a hyperbolu
, který průvodič bodu svírá s osou kuželosečky procházející tímto ohniskem.
Konstanta k udává úhel mezi původně
libovolně zvoleným směrem v rovině dráhy a směrem výše uvažované osy
kuželosečky. Konstanta k
je libovolná a odpovídá natočení kuželosečky ve vyšetřované rovině, je
ji možno určit z počátečních podmínek pohybu. V dodatku D.3 je
odvozeno, že pro elipsu a hyperbolu
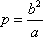 , , |
(4,44) |
kde a je velikost velké a b
malé poloosy. Pro parabolu parametr p
je roven vzdálenosti d ohniska od řídící přímky,
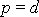 . Pro elipsu a hyperbolu má
. Pro elipsu a hyperbolu má
 význam numerické výstřednosti, tj. poměru
délkové výstřednosti e
k velikosti velké poloosy a,
význam numerické výstřednosti, tj. poměru
délkové výstřednosti e
k velikosti velké poloosy a,
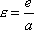 . . |
(4,45) |
Je tedy pro kružnici
 , pro elipsu
, pro elipsu
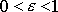 , pro hyperbolu
, pro hyperbolu
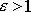 , nezávisle lze ukázat (viz dodatek D.3), že pro parabolu
, nezávisle lze ukázat (viz dodatek D.3), že pro parabolu
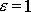 . Porovnáme-li právě učiněné závěry o hodnotách
. Porovnáme-li právě učiněné závěry o hodnotách
 s rovnicí
(4,42)
, dostaneme pro elipsu
z podmínky
s rovnicí
(4,42)
, dostaneme pro elipsu
z podmínky
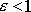 podmínku
podmínku
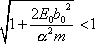 . . |
Protože však všechny členy obklopující
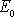 ve druhém sčítanci pod odmocninou jsou
kladné, je uvedenou nerovnost možno splnit pouze, když celková mechanická
energie pohybujícího se hmotného bodu je záporná;
ve druhém sčítanci pod odmocninou jsou
kladné, je uvedenou nerovnost možno splnit pouze, když celková mechanická
energie pohybujícího se hmotného bodu je záporná;
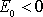 . Můžeme tedy shrnout, že z hodnot numerické výstřednosti
. Můžeme tedy shrnout, že z hodnot numerické výstřednosti
 plynou pro celkovou energii
plynou pro celkovou energii
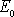 hmotných bodů obíhajících kolem centrální
hmotnosti M
po různých drahách tyto podmínky:
hmotných bodů obíhajících kolem centrální
hmotnosti M
po různých drahách tyto podmínky:
 . . |
(4,46) |
Omezíme-li se na případ
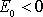 , je obsahem rovnice
(4,41)
první Keplerův zákon
. Představíme-li si, že centrální hmotnost M
je hmotnost Slunce a obíhající hmotné body
o hmotnostech m
jsou planety, lze obsah
rovnice
(4,43)
, která udává tvar dráhy hmotného bodu v silovém poli
(4,3)
vyslovit způsobem:
, je obsahem rovnice
(4,41)
první Keplerův zákon
. Představíme-li si, že centrální hmotnost M
je hmotnost Slunce a obíhající hmotné body
o hmotnostech m
jsou planety, lze obsah
rovnice
(4,43)
, která udává tvar dráhy hmotného bodu v silovém poli
(4,3)
vyslovit způsobem:
Planety obíhají kolem Slunce po elipsách, v jejichž jednom ohnisku leží Slunce.
Předpoklad
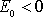 je zcela přirozený, protože dráhy pro
je zcela přirozený, protože dráhy pro
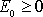 , tj. parabolická a hyperbolická dráha, nejsou uzavřené. Hmotný bod, který po
takové dráze do silového pole
(4,3)
vstoupí projde polem jednou a pak ho
opustí, vzdálenost r není omezená. Předpoklad
, tj. parabolická a hyperbolická dráha, nejsou uzavřené. Hmotný bod, který po
takové dráze do silového pole
(4,3)
vstoupí projde polem jednou a pak ho
opustí, vzdálenost r není omezená. Předpoklad
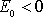 pro uzavřenou dráhu souvisí s volbou
nulové hodnoty potenciální energie
(4,6)
v nekonečnu. Pouze hmotné body,
jejichž celková energie je menší než potenciální energie v nekonečně
vzdáleném bodě, mohou se stále pohybovat v konečné vzdálenosti od
centrální hmotnosti M
pole
(4,3)
. Nejmenší energie, s kterou hmotný bod opustí pole
(4,3)
, je energie
pro uzavřenou dráhu souvisí s volbou
nulové hodnoty potenciální energie
(4,6)
v nekonečnu. Pouze hmotné body,
jejichž celková energie je menší než potenciální energie v nekonečně
vzdáleném bodě, mohou se stále pohybovat v konečné vzdálenosti od
centrální hmotnosti M
pole
(4,3)
. Nejmenší energie, s kterou hmotný bod opustí pole
(4,3)
, je energie
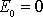 , které odpovídá parabolická dráha. Dosadíme-li podmínku
, které odpovídá parabolická dráha. Dosadíme-li podmínku
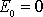 do rovnice
(4,33)
, dostáváme
do rovnice
(4,33)
, dostáváme
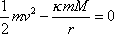 . . |
Dostáváme tak nejmenší velikost rychlosti v , kterou musí hmotný bod o hmotnosti m mít ve vzdálenosti r od středové hmotnosti M , aby mohl pole (4,3) opustit
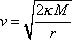 . . |
(4,47) |
Pokládáme-li středovou hmotnost M
za hmotnost Země a za r
zvolíme poloměr Země
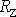 , dává rovnice
(4,47)
rychlost, jakou musí mít hmotný bod na povrchu Země, aby
mohl zemské gravitační pole opustit. Tato rychlost
, dává rovnice
(4,47)
rychlost, jakou musí mít hmotný bod na povrchu Země, aby
mohl zemské gravitační pole opustit. Tato rychlost
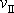 bývá označována jako 2. kosmická rychlost
. Pro její velikost dostáváme
bývá označována jako 2. kosmická rychlost
. Pro její velikost dostáváme
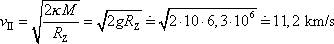 . . |
Při výpočtu rychlosti
 jsme užili rovnice
(4,10)
pro vyjádření výrazu
jsme užili rovnice
(4,10)
pro vyjádření výrazu
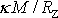 a dosadili jsme přibližné hodnoty
a dosadili jsme přibližné hodnoty
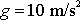 pro tíhové zrychlení g a
pro tíhové zrychlení g a
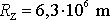 pro poloměr Země
pro poloměr Země
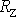 .
.
Všimneme si nyní pro eliptické dráhy
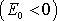 vztahu mezi konstantami
vztahu mezi konstantami
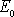 ,
,
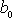 určujícími tvar dráhy a poloosami elipsy, tj. velkou poloosou a
a malou poloosou b. Vyjdeme z porovnání rovnic
(4,42)
a
(4,45)
; dostáváme
určujícími tvar dráhy a poloosami elipsy, tj. velkou poloosou a
a malou poloosou b. Vyjdeme z porovnání rovnic
(4,42)
a
(4,45)
; dostáváme
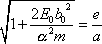 . . |
Poslední rovnici umocníme na druhou a pravou stranu upravíme dle vztahu
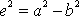 , který platí mezi poloosami a, b
a výstředností e
elipsy;
, který platí mezi poloosami a, b
a výstředností e
elipsy;
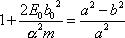 . . |
(4,48) |
Dle
(4,41)
je výraz
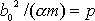 a dle
(4,44)
a dle
(4,44)
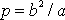 . Porovnáním dostáváme
. Porovnáním dostáváme
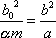 . . |
(4,49) |
Dosadíme-li tedy do druhého sčítance na levé straně
(4,48)
za
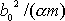 výraz
výraz
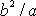 , dostáváme po úpravě
, dostáváme po úpravě
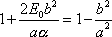 , , |
a tedy
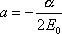 . . |
(4,50) |
Rovnice
(4,50)
ukazuje, že velikost velké poloosy elipsy závisí pouze na celkové
energii
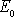 hmotného bodu a nezávisí na velikosti
momentu hybnosti
hmotného bodu a nezávisí na velikosti
momentu hybnosti
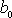 . Znaménko minus je přirozené, neboť
. Znaménko minus je přirozené, neboť
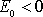 .
.
Dosadíme-li výsledek (4,50) do rovnice (4,49) , dostaneme po snadných úpravách
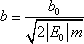 . . |
(4,51) |
Velikost malé poloosy b
elipsy závisí vedle
celkové energie
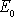 též na velikosti momentu hybnosti
též na velikosti momentu hybnosti
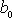 . Rovnice
(4,50)
a
(4,51)
byly využity v Bohrově modelu atomu
k elementárnímu kvantovaní energie a momentu hybnosti. K jedné
hodnotě energie jsou možné různé hodnoty momentu hybnosti, jednomu hlavnímu
kvantovému číslu odpovídá několik vedlejších kvantových čísel.
. Rovnice
(4,50)
a
(4,51)
byly využity v Bohrově modelu atomu
k elementárnímu kvantovaní energie a momentu hybnosti. K jedné
hodnotě energie jsou možné různé hodnoty momentu hybnosti, jednomu hlavnímu
kvantovému číslu odpovídá několik vedlejších kvantových čísel.
Odvodíme
nyní vztah mezi dobou oběhu hmotného bodu, který se v poli
(4,3)
pohybuje
po eliptické dráze a velikostí velké poloosy a
tohoto pohybu. Na začátku tohoto článku jsme odvodili větu, že
velikost plošné rychlosti
 při pohybu hmotného bodu v cent-rálním
silovém poli je konstantní. Z významu plošné rychlosti plyne, že násobek
plošné rychlosti
při pohybu hmotného bodu v cent-rálním
silovém poli je konstantní. Z významu plošné rychlosti plyne, že násobek
plošné rychlosti
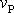 a doby T
oběhu bodu po uzavřené dráze musí být roven ploše uzavřené touto
drahou. Plocha P
elipsy o poloosách a, b je
a doby T
oběhu bodu po uzavřené dráze musí být roven ploše uzavřené touto
drahou. Plocha P
elipsy o poloosách a, b je
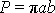 . Musí tedy pro uvažovanou eliptickou dráhu platit rovnice
. Musí tedy pro uvažovanou eliptickou dráhu platit rovnice
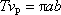 . . |
Dosadíme-li
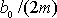 za
za
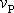 , dostáváme
, dostáváme
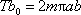 . . |
Za
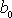 dosadíme z
(4,49)
a po elementárních úpravách
můžeme psát
dosadíme z
(4,49)
a po elementárních úpravách
můžeme psát
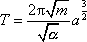 . . |
Rozepíšeme-li ještě
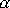 dle
(4,36)
, získáme konečný vztah
dle
(4,36)
, získáme konečný vztah
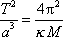 . . |
(4,52) |
Pro stálou centrální hmotnost M
je tedy poměr čtverce doby oběhu
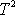 a třetí mocniny
a třetí mocniny
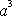 velké poloosy elipsy konstantní. Je-li
centrální hmotností Slunce a obíhajícími hmotnými body planety, je rovnice
(4,52)
obsahem tvrzení třetího Keplerova zákona, pro který bývá užívána následující formulace:
velké poloosy elipsy konstantní. Je-li
centrální hmotností Slunce a obíhajícími hmotnými body planety, je rovnice
(4,52)
obsahem tvrzení třetího Keplerova zákona, pro který bývá užívána následující formulace:
Poměr druhých mocnin oběžných dob libovolných dvou planet je roven poměru třetích mocnin jejich velkých poloos.
Elementárně lze dojít k tvrzení analogickému (4,52) , předpokládáme-li, že hmotné body obíhají kolem centrální hmotnosti M po kružnicích o poloměru r . Potom víme, že síla (4,3) realizuje dostředivou sílu (2,3) nutnou pro vznik kruhového pohybu, tedy
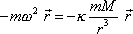 . . |
(4,53) |
Z vektorové rovnice (4,53) plyne skalární rovnice
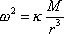 |
(4,54) |
a po dosazení známého vztahu
(1,26)
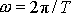 a jednoduché úpravě dostaneme
a jednoduché úpravě dostaneme
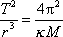 . . |
Tato rovnice odpovídá rovnici (4,52) , když se pohyb koná po kružnici. V tom případě poloměr r má stejný význam jako velká poloosa u obecného pohybu po elipse.
Rovnice
(4,54)
udává úhlovou rychlost, jakou se pohybuje volný hmotný bod po kružnici
poloměru r
v gravitačním poli
(4,3)
. Budeme nyní pokládat centrální hmotnost M
za hmotnost Země a vypočteme rychlost, jakou musí mít hmotný bod,
aby obíhal kolem Země v bezprostřední blízkosti Země. Takové rychlosti
vyjadřuje se obvykle jako postupná rychlost
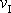 se říká první kosmická rychlost . Vypočteme její velikost. Z rovnice
(4,54)
plyne
se říká první kosmická rychlost . Vypočteme její velikost. Z rovnice
(4,54)
plyne
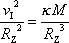 , , |
vyjádříme-li úhlovou rychlost pomocí rychlosti postupné a za poloměr r
dosadíme poloměr Země
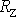 . Z právě uvedené rovnice vypočteme
. Z právě uvedené rovnice vypočteme
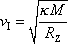 |
a dosadíme
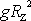 za
za
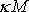 dle vztahu
(4,10)
. S uvážením číselných hodnot
dle vztahu
(4,10)
. S uvážením číselných hodnot
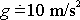 a
a
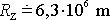 dostáváme pro první kosmickou rychlost vyjádření
dostáváme pro první kosmickou rychlost vyjádření
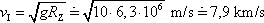 . . |
Rychlost
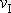 je přibližně rovna rychlosti, s kterou obíhají kosmické lodě kolem Země pohybující se na nízkých drahách.
je přibližně rovna rychlosti, s kterou obíhají kosmické lodě kolem Země pohybující se na nízkých drahách.